Autonomous Image Segmentation using Density-Adaptive Dendritic Cell Algorithm

Spatial data mining and particularly the task of image segmentation has been largely in focus of research in advanced computing applications like computer vision [1]. An optimal segmentation of images and identification of objectives therein are essential to understand an image clearly. Image segmentation involves partitioning an image into regions with similar properties such as gray level, color, and texture etc. The highly overlapped pixels and large amount of unpredictable and inestimable speckle noise in major image applications lead to severe difficulties. Modern data acquisition methods create a huge amount of image data for which manual analysis would be prohibitively expensive and time-consuming. Automatic segmentation of images in medical and geographical image analysis applications is a difficult task since these images rarely have any simple linear feature. For example in case of medical images, the output of segmentation algorithm is affected due to several causes namely partial volume effect, intensity inhomogeneity, presence of artifacts, and closeness in gray level of different soft tissue [2]. Several algorithmic techniques have been developed to address the challenges involved in image segmentation. A survey is reported in [3]. Profound supervised clustering methods facilitating or requiring user interaction, for example in hierarchical approaches such as relevance feedback techniques [4] have been in existence. However the purpose of autonomous image segmentation essentially emphasizes undertaking development of efficient unsupervised learning techniques aptly satisfying the concerns raised by continuously growing fields of applications. Density based clustering methods have been largely harnessed to cater to such needs.

Lately several propositions on application of the adaptive and the innate immune dynamics of the artificial immune systems (AIS) have been used to solve issues related to problems requiring supervised learning [5] or unsupervised learning including image segmentation. Most of the image segmentation models found in literature [6, 7, 8, 9, 10, 11] applied various formulations of the clonal principle of AIS. Such a model is computationally expensive and outcome is sensitive to the choice of the mutation parameter. The Dendritic Cell Algorithm (DCA) [12, 13] was formulated with infinite Gaussian mixture model in our previous work [14]. The experiments conducted on multivariate structured data set had showed the capability of the model to perform autonomous exploration of arbitrary shape of clusters. The clustering performed and the error rate were found to be comparable to those of the tests with same number of clusters generated through the standard K-means method. Yet the model was observed to be sensitive to initialization. The present work demonstrates adaptive-DCA formulated using the Gaussian mixture, wherein a necrosis-pressure gradient threshold has been introduced to control the splitting of clusters. This controlled splitting represents generation of antibodies only on certain aging of danger signals as per the danger theory [15, 16] of immune kinetics. The model was applied to the task of autonomous image segmentation. To obviate sensitivity to initialization, initially two clusters were generated through K-means applied over significant quantiles instead of the entire data. To ensure optimal solution several iterations of the EM runs were recorded and then the best solution was taken as the output. The experiment section details the properties of convergence and robustness of the algorithm investigated with synthetic as well as real images with presence of noise that have been. The segmentation quality was compared on basis of the PBM-index. This measure represents the proportion of the inter-cluster/intra-cluster affinities. To test the validity of the outcome, the Fuzzy C-Means (FCM) was executed over the same set of images and for the same number of clusters as generated autonomously by the adaptive-DCA. The high PBM-value generated with FCM in respective cases confirm the quality of the results generated by the adaptive-DCA.

In the following, section II presents a brief literature survey of related work identifying the issues and scope for the problem underhand. In section III design and algorith m of the Adaptive-DCA is described followed by description of the related implementation aspects contained in section IV. The results of the experiments and analysis of experiments are presented in section V. Section VI explores scope for improvement.

• II.    RELATED WORK

Probabilistic and stochastic modeling of images has substantially served in capturing the intrinsic characteristics of images in few parameters and in quantitatively specifying natural constraints of the phenomenon generating the images. Image modeling and analysis based on such methods focuses on the key issues of model selection, sampling, parameter estimation, and goodness-of-fits [17]. The core works that harness the principles of statistics for development of robust clustering methods have addressed to challenging issues like learning in the presence of missing data values and noises as in work by Martin [18], and to effectively speedup the learning [19]. The execution of image segmentation methods over huge pixel information is perceivably expensive considering the time and space complexities. Data clustering Models based on artificial immune systems (AIS) have addressed this issue. ARIA [20] demonstrated reduced memory usage yet comprehensive computation for extracting the inherent clusters. Another formalism blending AIS model with probabilistic distribution mixture model has been applied in INDIE [21] for the task of density estimation. They have employed the immune network metaphor of the AIS, which was earlier applied for clustering in aiNet [22]. The clustering methods applying operations over graph like recursive pruning of minimum spanning tree (MST) as in aiNet have yielded success in determining hierarchical clusters efficiently. However to determine optimal graph components automatically, we would have to consider applying such operations across several iterations to evaluate all possible groupings. A little effort on counting the candidate groups convinces that such formulation for autonomous segmentation mechanism would cause a NP-hard problem and hence not computationally viable. Among recent works to apply AIS mechanism in image segmentation, the work presented in [23] is remarkable. It has used the clonal principles of immune dynamics, which is computationally expensive. The method is applicable for K-segment determination when the number K of desired segments is pre-specified. Successful implementations of such models illuminate the pathway for development of efficient and robust image segmentation algorithm tuning in the probabilistic and stochastic models of immune dynamics for efficient autonomous computation of image segments. Several adaptations of the clonal principles of immune systems have been applied to solve optimization problems [7]. When the solution is represented by a vector of attributes imitated as antibodies of AIS, the population of candidate solutions may contain partial high quality solutions to the problem. The antibodies in the population might contain partial solutions to the global problem, which can be seen as building blocks of the clonal-AIS functionality. The authors of GAIS [24] observed that affinity maturation implemented in traditional cloning principle based AIS required cloning followed by the mutation of the newly-generated cells. Considering that the mutation operator cannot discover by itself crucial relationships among the variables of the problem, thus pinpointing the lack of ability to identify and effectively manipulate building blocks of the problem underhand. Bayesian formulation of the immune system functions was developed and applied to the task of multi objective optimization in MOBAIS [8] and was further refined in BAIS [9] for effective handling of the building blocks which also enhance its application to subspace learning problems like image segmentations. The model demonstrated in BAIS replaced the traditional mutation operator with a probabilistic model representing the probability distribution of the promising solutions found so far. Successful application of these models justified adoption of the Bayesian network as the probabilistic model, and reemphasized its capability to properly capture the most expressive interactions among the variables of the problem. Yang’s AIS model [11] for image segmentation using fused complementary features of image also applied the clonal principle for determining the optimal segmentation. The method applied pareto-ranking to search through the solution space. It can be observed that the above image segmentation methods based on clonal-AIS are computationally expensive and are highly sensitive to choice of the mutation parameter.

• III.    ADAPTIVE-DCA FOR AUTONOMOUS IMAGE SEGMENTATION

The prime goal of the work was to implement a program to determine segments in an image without need of human intervention. The recognition dynamics of the DCA was exploited to develop a self-adaptive segmentation model employing robust information exploration capabilities of statistical methods. An adaptation of the Dendritic Cell Algorithm (DCA), the danger theory based immune dynamics of the Dendritic Cells, was implemented as the first component of the model. The functional dynamics of the DCA is applied for recognition of incoming data; assigning them to one of the existing clusters or to create a new cluster in case of the danger signal. The second design component incorporated is the mixture of exponential family kernels to model pixel data in the current ‘window’ with respect to the mixture components; each mixture component being represented by a parameter-vector indicating individual image segments. In nutshell, an image segment is learned by the model as an antibody; which in turn would be implemented as a parameter-vector corresponding to an appropriately chosen distribution function. The stimulation level of an antibody on presentation of a new antigen resembles the posterior weights of a segment. The danger signals may be observed to resemble the outliers; memorizing the danger signal in newly created dendritic cells helps in finding out similar antigen (input data) in future input. Further splitting of a heavier (guarded by the threshold ‘eps’) but less dense cell taken in the context of clustering avoids over fitting of data. The clustersplitting threshold ‘eps’ taken here may be considered as the necrosis-pressure gradient threshold which controls generation of antibodies only on certain aging of danger signals as per the danger theory of immune kinetics. The infinite mixture models representing the components as their parameter-sets have been dependably applied in several algorithms to handle arbitrary shapes of clusters with reduced need for memory e.g. in [20]. On the other hand, the danger signal based splitting and merging steps of the Dendritic Cells immune function facilitates self adaptive learning of the inherent clusters. The learning method of the DCA avoids the redundant clone formation steps involved in the ‘Clonal Selection’ metaphor of AIS, thus giving quicker results. Moreover it avoids the dependency of such algorithm on the choice of mutation parameter. The estimation of the optimal mixture component through appropriately controlled EM convergence has largely been strategy of several evolutionary optimization algorithms [7, 8, 9, 25]. This combination therefore fulfils the need of effective autonomous image segmentation with reduced memory requirements.

DCKer nel()

Image Pixel values (Antigen)

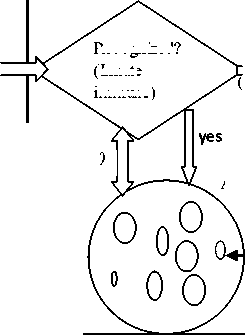
Recognized?

(Innate immune)

no signal)

ARB

Change

(Danger Detector

(Adaptive

immune)

Create new antibody

Figure 1. Block diagram of the danger model based Autonomous Segmentation Engine

• A. Algorithm

Input : Pixel intensity values of Image to find segments

Output : Antigen Types representing the corresponding image segments

Process:

• 1.    [Data Input] AG ^ Input antigens (image pixel values)

• 2.    [Reduce Noise] AG ^ Quantile-based noise reduction over input data in AG: Filter out the first and the last 5^th quantiles.

• 3.    [Initialise ARB with two DCs.] DCParam ^ Apply effective clustering method, e.g. K-means to determine initial representative centers (mean) of the first two DC-Kernels in the ARB.

• 4.    ARB ^ DCKernel (DCParam) [The DCs of ARB are implemented in form of the parameter vectors (DCParam), supported with corresponding vectors to store probabilistic affinity weights assigned to each data value in the input ‘Data’, as generated according to DCKernel() pdf with the respective DCparam values]

• 5.    For each Ag i ЄAG execute lines 6-11. ## Process Further Antigens (Data values)

• 6.    Find the affinity value with closest DC (in terms of probabilistic affinity weights for the Ag i in existing DCs in the ARB)

• 7.    If affinity < eps ( necrosis-pressure gradient threshold ) [Generate ‘ danger signal’ ]

• 8.    Create new DC in ARB (to memorise the danger signal), by assigning the new Ag i as its centre and other essential parameters of the recognizing DCKernel set accordingly.

• 9.    Update all DCs’ posterior affinity weights to include effects of addition of new cell.

• 10.    Otherwise, if size of closest DC is bigger than a size threshold, split the DC.

• 11.    Update age of antigens and the danger signals

• 12.    Update cell parameters

• 13.    Update DCs’ affinity weights for each antigen using revised DC-parameters.

• 14.    Compute likelihood value (Cluster quality) using log likelihood.

• 15.    Repeat through line 4 to obtain maximum likelihood estimation of clusters.

• IV.   IMPLEMENTATION ASPECTS OF THE ABOVE

ALGORITHM

• A.    K-means based initialization using quantile-filtered data

EM based learning methods are highly sensitive to initial component selection. Several techniques have been found in literature for good initialization of cluster components in evolutionary heuristics for unsupervised model selection problems. The need is satisfied by an efficient feature selection method suitable to the application. The solution in [11] for segmentation of images with fused complementary features employed the Gabor filter. Watershed filters have also been used in several other solutions. The image segmentation mechanis m provided in [25] used initial feature selection using the histogram properties, as the method used for clustering essentially performed grouping of the histogram components. In our algorithm the K-means based method was applied for initialization of the two initial clusters. The dataset was initially purged using quantiles in a way to avoid outliers.

• B.    Effect of the ‘eps’ keeping fixed versus adaptive

The parameter ‘eps’ guides generation of new cluster if certain data values don’t have the affinity to the closest segment greater than ‘eps’ threshold. It can be observed in the experimental results that setting up a uniform value for the parameter ‘eps’, to control splitting of the clusters, does not help evolve clusters. Therefore the parameter ‘eps was allowed to adjust as per the current minimu m affinity value given by (1).

eps new = min_affinity + (avg_affinity-min_affinity)/100.

Thus ‘eps’ might increase or decrease with generation of clusters and reassignments of the image points. The need for such adaptation was felt as the low value of ‘eps’ set manually to .002 was found sufficient to further with the next iteration but failed to split clusters while attempting subsequent iterations, as the update minimum affinity immediately after the first iteration was observed to be as high as .4014. Adapting the ‘eps’ slightly beyond the respective minimum affinity value with appropriate consideration of the range of affinities calculated as the difference of the minimum and the average values. Theoretically, such adjustment of the system parameter simulates the adaptive behavior of natural immune system. Such a formulation applied to autonomous image segmentation, generated convincing results as presented in the experimental result section. It might be argued that above adjustment of the ‘eps’ parameter might make the iterations caught in infinite generation of clusters if the input image was highly degenerate and originally no significant cluster was present; causing the ‘eps’ values to be very low even after dynamic adjustments. However, any such image would not be of any use either and we may assume with a note of practicability that the above formulation benefits in the target applications of image segmentation.

• C.    Convergence performed using  log-likelihood

computation

A threshold of 1E-20 for log-likelihood change was found sufficient to terminate the learning iterations with stable model estimation across several tests. The results varied across the subsequent conducted tests. The experimental result section shows respective outcomes with optimal values of the segmentation quality measure.

One among the alternatives for the loglikelihood measure for testing the convergence found in literature was the PBM- index [26]. However the PBM- index increases monotonically and tends hence its limiting behavior for C ^ N (C being the number of clusters detected and N is the length of the data set) is non-convergent [27]. So PBM is not so impressive index for controlling convergence of model estimation process. Another option proposed in [28] was of a point symmetry index (SI), which showed promising properties for pixel-wise assignment. But model estimation using this measure is computationally expensive if it is required to be computed several times during learning iterations. As the task of image segmentation does not emphasize exact pixel assignments, we find the log-likelihood estimation sufficient for our need.

• D.    Quality testing with PBM:

PBM- index was initially proposed by Pakhira [26] as a discriminant measure for unsupervised classification problems and has been used widely [11] for successful results in testing quality of clusters generated by respective algorithms. The PBM- index is defined as in (2).

(^

PBM (c) = | - x —1 x D\

I c —cc

Where c is the number of clusters such that,

• — = Z C = 1 — i ,

• ^—-■ = E " = i j x - v j II, and

D c = max c =i| v i ^- v j||

Here n is the total number of points in the data set, U(S) = [μij] c x n is a partit ion matrix for the data and vi is the center of the ith cluster. The objective is to maximize this index in order to obtain the actual number of clusters.

• V.   EXPERIMENTAL RESULTS

The development of the algorithm and its application to autonomous segmentation involved experiments conducted in two stages.

• A.    First Stage Experiment

In the first stage, tests over the convergence and segmentation properties of the Gaussian and the Poisson mixture components were performed; so that an appropriate formulation for the DCKernel() function be selected to estimate stimulation of DC on presentation of new antigen (a pixel value). The AIS based adaptive model presented in the algorithm above makes use of the density based kernels to add more and more clusters on finding a danger signal produced due to an antigen not activating any of existing antibodies. This adaptive model applies an infinite learning model; let us call the variations as the artificial immune Gaussian mixture model (AIGMM) and artificial immune Poisson Mixture model (AIPMM) respectively. The models were tested with a grey-level satellite image of landscape. The convergence of the learning algorithm was tested through maximization of log-likelihood of the posterior affinity weights, as given in the algorithm above. As observed in the visual outcome shown in figure 2, the Gaussian model converges earlier than the Poisson model; in fact convergence of later could not be achieved even until running the models until generation of 5 segments. As we observe in Figure 2, the segmentation achieved through the AIPMM shows slight modification in the right half of the image with more number of segments in comparison to those of the AIGMM. However, due to the difficulty of non-convergence of the AIPMM as compared to the assured convergence of the AIGMM, the former is considered an inferior choice for the model estimation purpose. The outcome of the AIGMM is comparable to that of the widely used segmentation method Fuzzy C-means (FCM), tested for generation of 3 segments. Observing the results of the AIGMM and the FCM in comparison with the original image, it is found that the AIGMM avoids the unnecessary segregation in form of extra black patches in the middle portion of the right half of image of FCM. The observation of the left upper portion also shows better ‘automatic’ segmentation by the AIGMM in comparison to FCM used for the same number of segments.

a)                    b)                     c)

d)                      e)                       f)

Figure 2: Image Segments generated: a) Original Image b) AIGMM:1.602sec c)FCM : 0.7836 sec. d) AIPMM: 2.74sec e) Log likelihood convergence plot for AIGMM f) Log likelihood convergence plots for AIPMM

• B.    Analysis of performance of Gaussian Mixture vis-à-vis Poisson Mixture based model estimation

The results of experiments conducted in the first stage indicated the use of the Gaussian mixture components to formulate the function DCKernel(); for computing the affinities of the antigens to the antibodies and guide further evolution of optimal sets of antibodies representing the image segments. Observed theoretically, the estimation of the Poisson mixtures uses only single parameter µ j that is the mean of each mixture component. In case two components generated during the evolution process have similar µ j values, they would in essence represent the same feature. If the means become equal, the two corresponding components would not be identified uniquely. Such evolutions during the learning process, would affect the convergence adversely and estimation becomes intractable. In such case the data points would have equally valid and significant affinity to each segment giving high likelihood, while on the contrary undesirable segments would be present. In case of the Gaussian mixtures variance or std. deviation is used as another parameter. A characteristic problem related to cluster assignment was argued in [29]. It is observed that in case of two components having close means, the component with the larger variance would be split. The resulting segment with smaller variance would have a higher likelihood so causing it to attract the points close to the common mean of the two segments. Thus the component with larger variance would contain the points farther from the mean, both high and low, although the later being disjointed in grey level. We observe that this problem of controlling the splitting of component is handled appropriately within the framework of the adaptive-DCA discussed below wherein the system parameter ‘eps’ is used to simulate the process of necrosis occurring during the self-adaptive natural immune system.

• C.    Second Stage Experiment

In the second stage experiments were conducted to test the image segmentation efficiency and other relevant properties of our algorithm. The quality of segmentation performed autonomously by our algorithm were then compared with those of the FCM executed for the same number of components as generated by the former, contrasted on the basis of the PBM measure. The results of experiments presented in subsequent section convincingly support viability of the proposition.

When tested for the synthetic data with Gaussian noise, as used above, setting up a uniform splitting threshold resulted into very few clusters when low and when set to a high value, it created numerous segments, impractical for acceptance. Following are the typical results representing outcomes of several executions for threshold value 0.002 with the five-segment image. When observed, the minimum probabilistic-affinity value was around .4 after the iteration progressed with the two resulting segments. Quite perceivably the subsequent iterations did not split segments beyond two.

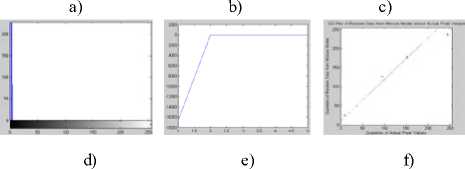
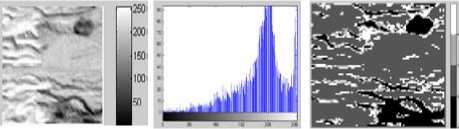
Figure 5. Segmentation with DCA having the necrosispressure-gradient applied over synthetic data with five segments: a) Image without Noise, b) Corresponding histogram, c) Image after segmentation d) Corresponding histogram, e)

Log-likelihood convergence plot, f) Q-Q plot

a)                    b)                     c)

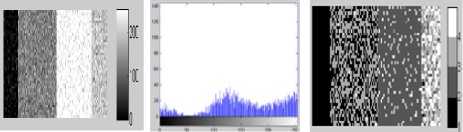
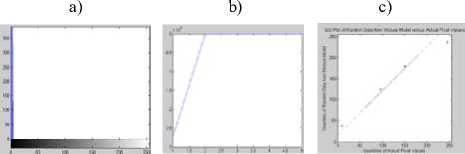
d)                        e)                   f)

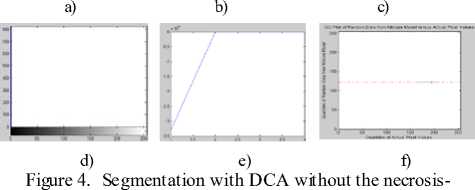
Figure 3. Segmentation with DCA without the necrosispressure-gradient applied over synthetic five segment image : a) Image with Gaussian Noise, b) Corresponding histogram, c) Image after segmentation d) Corresponding histogram, e) Loglikelihood convergence plot, f) Q-Q plot

• d)                            e)                           f)

Figure 6. Segmentation with DCA having the necrosispressure-gradient applied over synthetic data with four segments: a) Image with Gaussian Noise, b) Corresponding histogram, c) Image after segmentation d) Corresponding histogram, e) Log-likelihood convergence plot, f) Q-Q plot

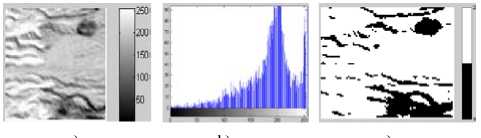
pressure-gradient applied over Landscape SAR Image: a) Image without Noise, b) Corresponding histogram, c) Image after segmentation d) Corresponding histogram, e) Loglikelihood convergence plot for EM, f) Q-Q plot

a)                      b)

c)

d)                          e)                           f)

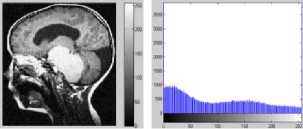
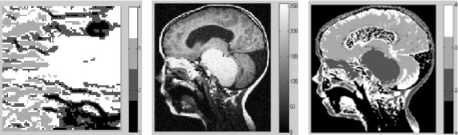
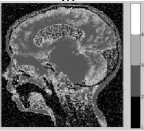
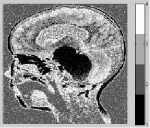
Figure 7. Segmentation with DCA having the necrosispressure-gradient applied over Brain MRI image: a) Image with Gaussian Noise, b) Corresponding histogram, c) Image after segmentation d) Corresponding histogram, e) Loglikelihood convergence plot, f) Q-Q plot

a)                        b)                       c)

f)

d)                         e)                           f)

Figure 8. Segmentation with DCA having the necrosispressure-gradient applied over Landscape SAR Image: a) Image without Noise, b) Corresponding histogram, c) Image after segmentation d) Corresponding histogram, e) Loglikelihood convergence

d)                           e)                           f)

Figure 9. Segmentation with DCA having the necrosispressure-gradient applied over Landscape SAR Image: a) Image with Gaussian Noise, b) Corresponding histogram, c) Image after segmentation d) Corresponding histogram, e) Loglikelihood convergence plot, f) Q-Q plot

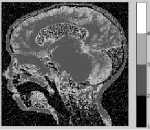
g)                   h)

Figure 10. Segmentation with FCM for K=4 to match with the result through the adaptive-DCA: a) Landscape SAR Image without noise b) segmented image c) Landscape SAR Image with Gaussian noise d) segmented image e) Brain MRI image without noise f) segmented image g) Brain MRI image with Gaussian noise h) segmented image

• D.    Analysis of autonomous model estimation with Gaussian mixture model employing adaptive splitting threshold for the DCA

As can be observed in the figures 5.c and 6.c, a stable solution typically detects 4 segments in both the synthetic images presented with Gaussian noise. Although the image reported in the first column was originally created with 5 segments; however, the histogram corresponding to the gray scale image shows that 4 modes dominate the distribution of pixel intensities. The two modes occurring in the middle of the histograms in figures 5.b and 6.b are less distinct though. Similar observation is drawn from the figures 7 and 8. The log-likelihood convergence graphs shown in figures (3-9).e and corresponding values in Table I in respective columns show the convergence of the algorithm. The quantile-quantile plots (Q-Q plots) between the actual data and the estimated mixture model, given in figures (3-9).f represent the segmentation quality. In case one or more plotted quantile-points deviate significantly beyond the diagonal, each case indicates a classification error. The respective Q-Q plots shown in figure (5-9).e are identical and quantiles fall closely along the diagonal. The outlying points in top right corners each indicate little classification error. The high PBM scores of the resulting model components corresponding to figures 5-9, as given in Table I indicate acceptability of the estimated segmentation.

Table I. Log-likelihood values obtained during consequent passes as represented in EM convergence plots in respective reference figures and the corresponding PBM values representing segmentation quality. Numbers within parenthesis along with each loglikelihood value represent the corresponding component counts; the optimal values are shown in bold letters. The PBM values shown are the typical average values across 10 executions of the segmentation estima tion.