Авроральная турбулентность ионосферной конвекции

Механизмы обратной связи между движущейся плазмой в магнитосфере и ионосфере предсказаны в работах [1; 2]. В холодной плазме из-за столкновений с нейтральными частицами в ионосфере возникают возмущения электрического и магнитного полей, распространяющиеся вдоль магнитного поля из ионосферы в магнитосферу в форме альвеновской волны. Из-за поляризационных токов на краях области возмущения возникают продольные токи, которые направлены вдоль магнитного поля и могут приводить к возникновению продольного электрического поля, ускорению и высыпанию электронов в ионосферу. Данная обратная связь может стать положительной и привести к нарастанию возмущений. Исследования обратной связи проводятся, как правило, в приближении малых возмущений [3; 4]. Но даже в этом случае более точное решение этой задачи получается при использовании только численных методов, что связано с достаточно неоднородным профилем альвеновской скорости вдоль магнитной силовой линии. Значительные по величине продольные токи (10 ^–5 А/м ² ) могут заметно модифицировать ионосферную проводимость, в то же время оказывая малое влияние на концентрацию холодной магнитосферной плазмы. Таким образом, процессы, описывающие обратную связь, могут быть нелинейными в ионосфере и линейными в магнитосфере. В рамках данного приближения с учетом реалистичного изменения альвеновской скорости вдоль магнитной силовой линии в настоящей работе численно исследовано развитие двумерного аврорального возмущения.

Описание ионосферы

Используем прямоугольную систему координат, ось y направим на запад, ось x к – югу, ось z – вниз, вдоль магнитного поля (Северное полушарие). Рассмотрим двумерные возмущения, зависящие от x и z, т. е. ∂/∂y = 0.

Уравнение непрерывности для электронов с учетом процессов ионизации и рекомбинации имеет следующий вид:

∂n/∂t + ∂(nv _ex )/∂x = –γ/e∂j _z /∂z– r(n ² – n ₀ ² ),                                  (1)

где n, v ex – концентрация и скорость электронов; n 0 – фоновое значение концентрации; r – коэффициент рекомбинации (квадратичный закон рекомбинации выполняется для высот E-слоя); j z – продольный ток; e – заряд, равный заряду электрона; γ – коэффициент размножения пар ионов при ионизации.

Проанализируем процессы, длительность которых много больше 0.01 с. В этом случае из уравнения движения ионов получим следующее выражение для скорости:

v xi = (–kT∂ln(n)/∂x + eE x )f(ν in /ω i )/m i ω i ,                                      (2)

где v _xi – скорость ионов; kT – тепловая энергия ионов; m _i – масса иона; n – концентрация ионов в ионосфере; ν in – частота столкновений ионов с нейтралами; ω i – гирочастота ионов; E x – напряженность x-компоненты электрического поля; f(ν in /ω i ) = (v in /ω i ) /(1 + (v in /ω i ) ² ).

Уравнение непрерывности для тока в ионосфере имеет вид

∂/∂x(σ p E x – σ h E 0y )= –∂j z /∂z,                                       (3)

где σ p , σ h – ионосферные проводимости Педерсена и Холла; E 0y – электрическое поле ионосферно-магнитосферной конвекции.

Частоты столкновений электронов с нейтралами много меньше гирочастоты электронов в ионосфере, поэтому можно считать, что электроны движутся со скоростью конвекции v e = E 0y /B 0 , где B 0 – индукция магнитного поля в ионосфере. Ионосферные проводимости зависят от концентрации заряженных частиц и частот следующим образом:

σ h = en/B 0 , σ p /σ h ≈ f(ν in /ω i ).

В дальнейшем будем рассматривать ионосферу как тонкий проводящий слой. Уравнения (1)–(3) проинтегрируем по толщине ионосферы h. Для этого зададим изменения концентрации с высотой s: n(s) = n ₀ exp(–(s – s ₀ ) ² /h ² ), где s ₀ – высота максимума E-слоя, изменение функции f с высотой зададим похожим образом с f(s 0 ) = 0.5 [5].

Проинтегрированные по толщине ионосферы уравнения (1), (3) запишем так:

∂^/∂t + E 0y /B 0 ∂^/∂x = –γj z /e– r(^ ² – ^ 0² )/(2 ^3/2 h),                             (4)

∂/∂x(e^E x /(2 ^3/2 B 0 ) – kT∂ln(^)/∂x/(2 ^3/2 eB 0 ) – e^E 0y /B 0 ) = j z .                         (5)

Описание магнитосферы

Магнитосферную плазму считаем холодной, возмущением концентрации плазмы пренебрегаем, продольные электрические поля равны нулю. Единственной компонентой возмущенного электрического поля является E _x , магнитного – H _y . Из уравнения движения для холодной плазмы в магнитном поле в системе координат, движущейся вместе с плазмой, получим выражение для поляризационного тока в альвеновской волне:

j x = 1/(µ 0 v a² )∂E x /∂t,                                                 (6)

где µ 0 – магнитная проницаемость вакуума; v _a ² = ρµ 0 /B ² – квадрат альвеновской скорости; ρ – плотность плазмы; B – индукция магнитного поля в магнитосфере.

Из уравнений Максвелла ∂E _x /∂z = –µ ₀ ∂H _y /∂t, ∂H _y /∂z = –j _x , ∂H _y /∂x = j _z и уравнения непрерывности для тока ∂j _z /∂z = – ∂j _x /∂x получим уравнения для E _x и j _z :

∂ ² E x /∂z ² = 1/(v a² )∂ ² E x /∂t ² ,                                             (7)

∂j z /∂t = –1/(µ 0 ) ∂ ² E x /∂z∂x.                                          (8)

Магнитные силовые линии считаем прямыми, но расходящимися, пренебрегаем углом наклона магнитного поля Земли к ионосфере. Индукция магнитного поля изменяется с расстоянием r от центра Земли по закону B = B 0 (r з /r) ³ , где r з – радиус Земли. Концентрация магнитосферной плазмы (протоны) n = n ₀ exp(–(r/2r _з ) ² ), где n ₀ – концентрация в ионосфере. Профиль изменения альвеновской скорости от ионосферы z = 0 до экваториальной плоскости магнитосферы z = –(r – r _з )/r _з = –10 показан на рис. 1. Значения z убывают с удалением от Земли (от верхней границы ионосферы). Концентрацию плазмы в ионосфере при z = 0 зададим равной n 0 = 0.5·10 ¹¹ 1/м ³ .

Граничные условия

Для решения уравнения (7) необходимо записать граничные условия для E _x на нижней (ионосфера) и верхней (экваториальная плоскость) границах. В движущейся системе координат уравнение (5) не меняется, а в уравнении (4) пропадает второе слагаемое в левой части. Получим условие на нижней границе. Продифференцируем уравнение (5) по времени, исключим ток j z , воспользовавшись выражением (8), опустим производную по x, в итоге получим при z = 0

∂E x /∂t = –(E x – 2 ^3/2 E 0y )∂(ln^)/∂t – 2 ^3/2 B 0 /(eµ 0 ^)∂E x /∂z + kT/(e ² ^)∂ ² (ln^)/∂z∂t.              (9)

На верхней границе при z = –10 зададим

∂E x /∂z = 0.                                              (10)

Это условие определяет узел для магнитного поля на экваториальной границе (E _x = 0 – узел для электрического поля).

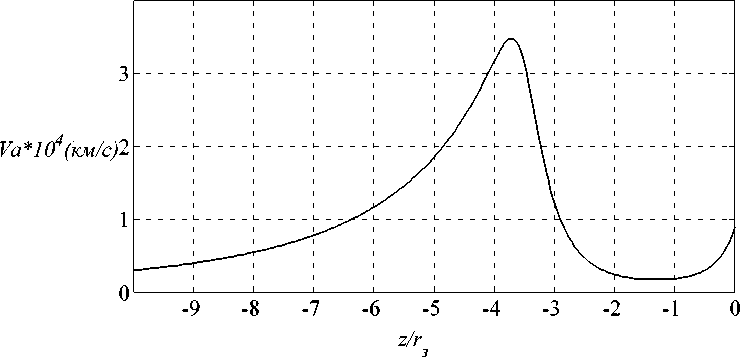
Рис. 1. Изменение альвеновской скорости вдоль магнитной силовой линии от ионосферы при z = 0 до экваториальной плоскости магнитосферы при z = –10

Результаты численного моделирования

Систему уравнений (4), (7), (8) при граничных условиях (9), (10) решим посредством численного интегрирования с шагом по времени dt = 0.005 с, с шагом по координатам dx = 100 м и dz = 100 км соответственно. Начальное возмущение компоненты E _x электрического поля (поле в падающей на ионосферу альвеновской волне) на ионосферном уровне длительностью τ = 4 с зададим в форме гауссоиды по x:

E x (x) = E x0 exp(–((x–L/2)/dL) ² ),                                    (11)

где E x0 – амплитуда возмущения, заданная равной 5 мВ/м; L = 100 км – размеры области интегрирования по x; dL – пространственный масштаб изменения начального возмущения по координате x; dL = v x0 τ, здесь v x0 = E 0 /B 0 – скорость конвекции. Примем скорость конвекции v x0 = 500 м/c, получим dL = 2 км. На правой границе при x = L выполняется условие

∂E x /∂t – (dx/dt)∂E x /∂z = 0.                                      (12)

Данное условие означает прозрачность правой границы области интегрирования.

На рис. 2, а, б, в приведены результаты численного моделирования концентрации ^, компоненты Ex электрического поля, продольного тока j на ионосферном уровне в разные моменты времени. Расчет проведен с учетом значения параметра γ = 10, интегральной ионосферной проводимости Холла, равной 8 См, что соответствует достаточно возмущенным условиям. Время нарастания возмущений согласно приведенным расчетам составляет ~60 с, время распространения альвеновской волны до экваториальной плоскости и обратно – ~40 с. С уменьшением проводимости ионосферы время нарастания возмущений сокращается. Несмотря на значительные продольные токи, достигающие 10 А/км2, изменение ионосферной электронной концентрации очень незначительно в приведенных расчетах, что связано с малым значением параметра γ, который определяет количество пар ионов, образующихся при ионизации одним электроном. В дугах сияний этот параметр может быть больше 100. Исследовано влияние диффузии на развитие возмущений, она ослабляет и даже подавляет нарастание возмущений. Можно оценить на основании данных, представленных на рис. 2, скорость распространения возмущения. Она направлена в сторону, противоположную конвекции плазмы, и приблизительно равна 100 м/c. Такое движение дуг относительно ионосферной плазмы с близкой по величине скоростью наблюдается экспериментально [6].

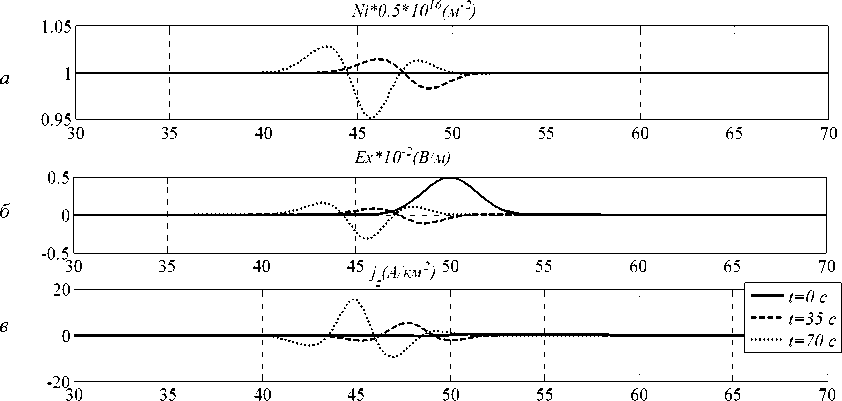
х(км)

Рис. 2. Развитие ионосферных возмущений, инициированных импульсом электрического поля E _x в момент времени t = 0 длительностью τ = 4 с

t=35 c

-9       -8       -7       -6       -5       -4       -3       -2       -1        0

t=70 c                                           Ех*10"2(В/м)

0.2

0.1

-0.1

0.2

-0.2

-8

-6

-4

-3

-1

-9

-7

-2

-5 z/r

з

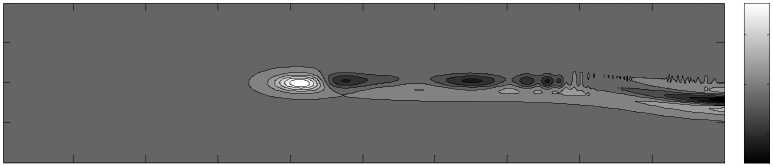
Рис. 3. Распространение возмущения E x вдоль магнитного поля из ионосферы при z = 0 в магнитосферу

На рис. 3 приведены распределения компоненты E x электрического поля в разные моменты времени. Величина напряженности электрического поля увеличивается в зависимости от времени и расстояния от ионосферы, достигая 3 мВ/м; в ионосфере поле значительно меньше. Поперечные мелкомасштабные структуры электрического поля часто наблюдаются в авроральной магнитосфере [7].

Выводы

Задача развития возмущений в движущейся ионосферной плазме рассмотрена с использованием методов численного моделирования. Расчеты выполнены в двумерном приближении для возмущений, имеющих масштаб поперек магнитного поля ~1 км в одном направлении и неограниченный масштаб в другом. В ионосфере процессы рассмотрены как нелинейные, в магнитосфере использовалось линейное приближение. Плазма в магнитосфере считалась холодной. Линейное уравнение распространения возмущений вдоль магнитного поля из ионосферы в магнитосферу решено с учетом изменения скорости вдоль магнитного поля.

Время нарастания возмущений с масштабом ~1 км составляет ~60 с (для возмущенной ионосферы проводимость Холла в расчетах равна 8 См) и зависит от проводимости ионосферы; с уменьшением проводимости возмущения развиваются быстрее. Возмущения на меньших масштабах также развиваются быстрее.

Учет теплового движения частиц в ионосфере приводит к ослаблению и даже подавлению развития ионосферных возмущений.

Значительные продольные токи (до 10 A/км ² ) вызывают незначительные изменения концентрации ионосферной плазмы, что связано с недооценкой ионизационного члена в уравнениях.

Скорость движения возмущений поперек магнитного поля относительно скорости конвекции составляет ~100 м/c.

Напряженность электрического поля возмущения растет с удалением от ионосферы и достигает максимума в магнитосфере вблизи экваториальной плоскости.