Авроральные неоднородности и Фарлей-Бунемановская неустойчивость

В возмущенной полярной ионосфере образуются особые анизотропные мелкомасштабные неоднородности, большие оси которых ориентированы вдоль силовых линий магнитного поля Земли (авроральные неоднородности). Отличительная особенность этих неоднородностей состоит в том, что они порождают интенсивное обратное рассеяние радиоволн УКВ и СВЧ диапазонов.

В соответствии с теорией слабого рассеяния радиоволн (Рытов и др., 1978), основной характеристикой энергетических свойств обратного рассеяния является поперечник рассеяния единичного объема

σ0 (2k, τ) = 8π3 re2 (ΔN )2 Φ0 (2k, τ).(1.1)

Он зависит от волнового вектора радара k , классического радиуса электрона r_e = 2.8 ⋅ 10 ^{- 15} ì, концентрации электронов в неоднородности Δ N и пространственно-временного энергетического спектра Φ 0 ( 2 k , τ ). Пространственно-временной энергетический спектр

Φ0 (2k, τ) = 1 / (8π 3) ∫ B0 (ρ, τ) exp (- j2k ρ ) d 3ρ(1.2)

представляет собой Фурье-преобразование от нормированной автокорреляционной функции

B0 (ρ, τ) = 〈n (r, t) n∗ (r + ρ, t + τ)〉 / 〈 n (r, t) n∗ (r, t)〉,(1.3)

в которой n ( r , t ) - функция, характеризующая зависимость концентрации неоднородности от координат и времени, n ^∗ - комплексно-сопряженная функция, τ - сдвиг по времени, ρ - сдвиг по пространству.

Из (1.1) - (1.3) видно, что для теоретического расчета поперечника  σ0 нужно знать пространственно-временной закон изменения концентрации неоднородности n(r, t).

Анализируя специфические особенности авроральных радиоотражений, Букер пришел к выводу, что авроральные неоднородности должны иметь столбообразную форму с большими осями, ориентированными вдоль силовых линий магнитного поля Земли (Booker, 1956a). Из его оценок следовало, что размер неоднородностей L вдоль магнитных силовых линий должен быть не менее 10 ì, а поперечный размер Т не должен превышать 0.1 ì. Задавшись гауссообразной формой неоднородности n (r) = ΔN exp [ - (x2 + y2) / T02 - z2/ L2]                                (1.4)

и рассчитав с ее помощью автокорреляционную функцию (1.3), Букер получил выражение для поперечника обратного рассеяния авроральных неоднородностей ( Booker , 1956a)

σ 0 (2 k ) = (2 π ) ^1.5 r e ² ( Δ N )² T 0 ² L exp ( - 2 k ² T 0 ²) exp ( - 2 k ² L ² sin² Ψ ),           (1.5)

где Ψ - ракурсный угол между волновым вектором радара k и плоскостью, перпендикулярной магнитной силовой линии (ось Z ).

Но простейшая букеровская модель (1.4) не содержит в себе зависимости от времени t, т.е. она не отвечает на вопрос о том, как в полярной ионосфере формируются столь необычные структуры. Букер представлял себе механизм их образования следующим образом. На высотах Е-области ионосферы коэффициент амбиполярной диффузии электронов вдоль магнитных силовых линий примерно на два порядка превышает поперечный коэффициент диффузии. Поэтому любая изотропная неоднородность n0(r), возникшая на этих высотах, быстро расплывается вдоль магнитных силовых линий и превращается в анизотропную неоднородность.

Основная трудность в обосновании этой модели состояла в том, чтобы указать источник появления в ионосфере исходных мелкомасштабных изотропных неоднородностей n 0 ( r ) с начальным размером T 0 , не превышающим 0.1 ì. Букер понимал, что тепловые флуктуации ионосферной плазмы для этой цели непригодны в силу чрезвычайной малости времени их жизни. Время их жизни, как известно ( Арцимович и др ., 1979), обратно пропорционально плазменной частоте ro P , т.е. имеет величину порядка

10^-7ñ. За столь короткий промежуток времени изотропные неоднородности, порождаемые тепловыми флуктуациями, не могут приобрести сколько-нибудь заметную анизотропию и всегда остаются изотропными. Поэтому Букер (1956b) предположил, что источником образования исходных мелкомасштабных неоднородностей с размером T 0 <  0.1 м служат не тепловые флуктуации, а турбулентные процессы в ионосферной плазме.

В соответствии с колмогоровскими представлениями о развитии турбулентных процессов ( Татарский , 1967) они протекают по следующей схеме. Вначале возникают крупномасштабные плазменные неоднородности, концентрация в которых быстро нарастает. Затем эти крупномасштабные неоднородности становятся неустойчивыми, и начинается их лавинообразный распад на неоднородности со все более и более мелкими масштабами. Распад продолжается до тех пор, пока мелкомасштабные неоднородности не достигнут некоторой минимальной величины T _min. После этого распад прекращается, а образовавшиеся мелкомасштабные неоднородности T min исчезают в результате обычного процесса диффузионного расплывания. Эти долгоживущие мелкомасштабные неоднородности - конечный продукт распада крупномасштабных, и служат, по мнению Букера, основой для формирования авроральных неоднородностей.

Принципиальная трудность, с которой столкнулся Букер при обосновании этой модели, заключалась в оценке минимальных размеров неоднородностей T _min, образующихся в результате турбулентного распада. Если исходить из известных экспериментальных оценок параметра турбулентности, то минимальный размер неоднородностей получается T min ~ 6 м ( Гершман, 1974), тогда как в букеровской модели он не должен превышать T min <  0.1 м. Букеру не удалось преодолеть это противоречие, и его физическая модель образования авроральных неоднородностей не получила признания.

На смену ей пришла другая модель, базирующаяся на результатах работ Фарлея ( Farley , 1963) и Бунемана ( Buneman , 1976). Эти авторы рассмотрели задачу об устойчивости плазмы на высотах E-области ионосферы и показали, что тогда, когда средняя дрейфовая скорость электронов V_e0 превышает скорость ионного звука V_S , плазма на этих высотах становится неустойчивой. В ней происходит экспоненциальный рост амплитуд плоских волн концентрации, распространяющихся ортогонально магнитным силовым линиям.

Этот результат применительно к авроральным радиоотражениям обычно трактуется следующим образом. В плазме существуют неоднородности концентрации, порожденные тепловыми флуктуациями. Каждую из них можно разложить в пространственный спектр плоских волн n теп ( k ). Амплитуды гармоник этого спектра невелики, и обычный локатор не способен зарегистрировать отраженный от них сигнал. Но если в плазме развивается Фарлей-Бунемановская (Ф-Б) неустойчивость, амплитуды гармоник нарастают (рис. 1), и когда они достигают требуемой величины, локатор регистрирует отраженный сигнал.

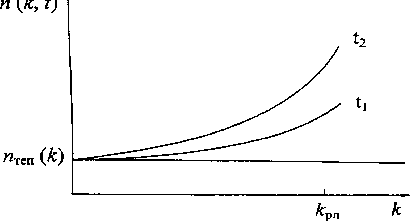
Рис. 1. Обычная трактовка задачи о развитии Ф-Б неустойчивости. Плоские волны концентрации тепловых флуктуаций n _теп( к ) нарастают с течением t ( t₂ >  t 1 ). В момент t 2 локатор с волновым числом k рл регистрирует отраженный сигнал

Отличие такой трактовки задачи от букеровской состоит в том, что первопричиной авроральных радиоотражений в ней считаются не турбулентные процессы, а тепловые флуктуации плазмы. Поэтому наличие или отсутствие плазменной турбулентности и связанная с ней проблема минимальных размеров неоднородности T min для данной модели несущественны.

Цель нашей работы - показать ошибочность такой трактовки задачи. Мы увидим, что причина ее ошибочности кроется не в самой идее Фарлей-Бунемановской неустойчивости, а в изначальной постановке задачи. В основополагающих работах Фарлея и Бунемана задача рассматривалась в такой формулировке, которая позволяла авторам ответить на главный вопрос теории -вопрос об условии возникновения неустойчивости в слабоионизованной замагниченной плазме. Но знание только этого условия еще недостаточно для ответа на вопрос о том, каковы при этом будут закономерности обратного рассеяния радиоволн. Для ответа на этот вопрос задача о развитии Ф-Б неустойчивости должна формулироваться в несколько иной форме. Мы увидим также, что при другой формулировке задачи обнаруживается прямая связь между Ф-Б неустойчивостью и букеровской моделью образования авроральных неоднородностей. При этом в букеровской модели, дополненной Ф-Б неустойчивостью, исчезает проблема малого начального размера исходной неоднородности Tmn < 0.1 1, и сама модель обретает четкий физический смысл.

• 2.    Традиционная формулировка задачи

  Рассмотрим, следуя ( Гершман , 1976), линеаризованную систему гидродинамических уравнений слабоионизованной плазмы, дополненную уравнением Пуассона:

д Ve I дt = - e me-1 (E + c-1 Ve x H0) - ve Ve - VT e2 V ne I no д Vi / дt = e mi-1 (E + c-1 Vi x H) - vi V, - Vt i2 V n I no дne / дt + no V Ve + Ve 0 V ne = 0                                             (2.1)

д n i / д t + n o V V i + V i 0 V n i = 0

V E = 4 n e ( n i - n e ).

В (2.1) обозначено: V e , V i , n e , n i и E - малые отклонения скоростей электронов, ионов, их концентраций и электрического поля от стационарных значений V_{e 0} , V_{i 0} , n_o , E _o ; v _e и v i - частоты столкновений электронов и ионов с нейтральными частицами; V_Te ² = T_e / m e и V_Ti ² = T i / m i - среднеквадратичные значения тепловых скоростей электронов и ионов; T e , T i , m e и m i - их температуры и массы; e - заряд электрона; H 0 - вектор напряженности магнитного поля.

Записав все входящие в (2.1) переменные V e , V i , n e , n i и E в виде обратного преобразования Фурье от их спектрального разложения S ( m, к )

S ( r , t ) = JJ S ( m, к ) exp { j' ( m, t - к r )} d m d k ,                               (2.2)

придем к системе алгебраических уравнений относительно S(m, к). Эта система после ряда упрощений, связанных со спецификой плазменных процессов на высотах Е-области ионосферы (возможность пренебрежения инерцией электронов, специфические соотношения между гирочастотами электронов и ионов mHe, mHi и частотами их столкновений с нейтралами mHe >> ve, mHi << vi, пренебрежимо малая средняя скорость ионов Vi 0 ~ 0 и т.п.) приобретает вид e me-1 E = - mHe Ve x Ho I Ho - Ve Ve + j к Vte2 ne I no (2.3) e m,-1 E = (j m + v) V, - j к Vti2 n I no (2.4) ne I no = к Ve I (m - к Ve o) (2.5) ni I no = к Vi I m (2.6) к E = j 4 n e no (ni I no - ne I no). (2.7)

При традиционном способе решения этой системы из нее вначале исключаются концентрации электронов и ионов (2.5), (2.6). В результате получаются три векторных уравнения относительно E , V e и V i . Записав их в проекциях на оси декартовой системы координат и исключив проекции векторов V e и V i , приходят к системе трех однородных уравнений относительно E x , E y и E z ( Гершман , 1976)

• a_n E x + a i2 E y + a i3 E z = 0

a 2i E x + a 22 E_y + a 23 E z = 0                                     (2.8)

• а з1 E x + а з2 E y + а зз E z = 0.

Поскольку система однородных уравнений (2.8) может иметь нетривиальное решение только в том случае, когда ее определитель равен нулю

а11 а21 а12 а22 а1з а23 = 0, (2.9) а31 а32 а33 то условие (2.9) приводит после ряда упрощений к соотношению

^{1 + m} o i ² / [ ^{- m ( m - j v} i ) ^{+ k 2} V T i ² ] ^{+ m} o i ² / [ ^{j v} i R -1 ^{( m - к V}e o ) ^{+ k} 2 V T i ² ] = °- ⁽².¹⁰⁾

В нем обозначено m o i = (4 n e ² n_o I m i )^1/2 - плазменная частота ионов, и введен коэффициент

R = v i- v o I m Hi m He [1 + ( m He ²1 v e ²) sin² V ].                                     (2.11)

Воспользовавшись неравенством moi2 >> k2 VTi2, справедливым для низкочастотных колебаний, в (2.10) пренебрегают единицей и получают квадратное уравнение относительно m ю2 - j vi (1 + R) R -1 ю + j vi R -1 k Ve - k2 VS2 = 0,                             (2.12)

где Vs = 21/2 VT - скорость ионного звука. Полагая в этом уравнении частоту ю комплексной ю = Q - j у, сводят его к двум уравнениям, первое из которых для декремента у у2 + vi (1 + R) R-1 у + k2 Vs2 - Q2 = 0,                                (2.13)

а второе - для частоты Q

Q [ v i (1 + R ) R ^{- 1} + 2 у ] = v i R ^{- 1} k V e 0 .                                   (2.14)

Считая у <<  v i (1 + R ) R ^{- 1}, находят частоту плазменных волн

Q = k V e 0 / (1 + R ),                                          (2.15)

а из первого уравнения - выражение для декрементов

У 1,2 = -v i (1 + R ) (2 R ) ^{- 1} ± v i (1 + R ) (2 R ) ^{- 1} X [1 - 4 R ² ( k ² V s ² - Q ²) / v i ² (1 + R ²)]^1/2.

Для интересующих нас ракурсных углов V ~ 0 коэффициент R << 1, и приближенные выражения для декрементов приобретают вид у 1» - R { k2 Vs2 - [ k Ve 0 / (1 + R) ]2} / vi (1 + R),                       (2.16)

у 2 « - v i (1 + R ) R ^{- 1}.                                       (2.17)

Из (2.16) видно, что при условии k Ve 01 (1 + R) > k Vs,                                     (2.18)

декремент у 1 меняет свой знак и превращается в инкремент. Неравенство (2.18) и есть условие возникновения Ф-Б неустойчивости. При его выполнении амплитуды плоских волн спектра S ( c , k ) в (2.2) нарастают по экспоненциальному закону S ( щ k ) exp ( у 1 Д. Это общее утверждение относится ко всем переменным системы (2.3) - (2.7).

• 3.    Возможность сопоставления теории с экспериментом

Для сопоставления теории Ф-Б неустойчивости с авроральными радиоотражениями необходимо знать поперечник рассеяния единичного объема (1.1). Его расчет, как уже говорилось, требует знания пространственновременной зависимости концентрации неоднородностей n( r , t) или связанной с ней (см. 2.2) спектральной функции n(ю, k ). Для того, чтобы проиллюстрировать возникающие здесь трудности, разрешим систему (2.3) - (2.7) относительно интересующих нас функций n e / n_o и n i / n_o . Последнее осуществляется следующим образом.

Умножив уравнение (2.7) на e / mi, а уравнение (2.4) на k и сравнив их, получим юо i2 (ni / no - ne / no) = (ю - j vi) k Vi - k2 Vti2 ni / no.

Подставив сюда k V i из (2.6), найдем первое уравнение системы

[ ю о i ² - ю ( ю - j v i ) + k ² V t i ² ] n i / n o - ю оi ² n e / n o = 0.                            (3.1)

Аналогичным образом, умножив (2.7) на e / m e , а (2.3) на k и сравнив их, получим с учетом (2.5)

j ю o e ² ( n i / n o - n e / n o ) = - ю нe k ( V e x H o / H o ) - v e ( ю - k V e o ) + j k ² V t e ² n e / n o ,                (3.2)

где ю _0e = (4 n e ² n_o / m e )^1/2 - плазменная частота электронов.

Входящее в (3.2) скалярно-векторное произведение приобретает после сравнительно несложных преобразований вид (см. Приложение)

k ( V e X H o / H o ) = ю н e Y e -¹ k V e / (1 + ю н e ² Y e -2 sin 2 V ).

Его подстановка в (3.2) с учетом (2.11) и соотношений юoe2 = mi me-1 юoi2, VTe2 = mi me-1 VTi2 дает второе уравнение системы юo i2 nt / no - [ j vi R-1 (ю- k Ve o) + k2 Vti2 + юo i2 ] ne / no = 0.

(3.3)

(3.4)

(3.5)

Обозначив в (3.1) и (3.3)

k ² V T i ^{2 - ю ( ю - j v )} = A , k ² V t , ² + j v i R ^{- 1} ( ю - k V e o ) = B , запишем систему двух однородных уравнений в виде

( ю o i ² + A ) n i / n o - ю o i ² n e / n o = 0 - ю o i ² n i / n o + ( ю o i ² + B ) n e / n o = 0.

Эта система, как и (2.8), имеет нетривиальное решение лишь при равенстве нулю ее определителя

^{( ю} 0i ^{2 +} А )      - ^ю 0i

^{- ю} 0i ²     ( ю 0i ² + В )

= ю _о , ² ( А + В ) + АВ = 0                     (3.6)

Поделив (3.6) на AB , придем к обычному виду дисперсионного уравнения (2.10)

1 + ю о i ² / A + ю о i ² / B = 0, из которого после пренебрежения единицей получается квадратное уравнение (2.12)

A + B = Ю - j v i (1 + R ) R ^{- 1} ю + j v i R ^{- 1} к V e _о - k ² V S ² = 0.                   (3.7)

Но, в отличие от формального условия (2.9), физический смысл условия (3.6) достаточно прозрачен. Если в системе координат n e и n i записать исходную систему (3.5) в виде двух уравнений прямых, проходящих через начало координат

П е ( ю, к ) = (1 + A / ю о i ²) n ( ю, к ), П е ( ю, к ) = (1 + B / ю о i ² ) ^{- 1} n ( ю, к ),

(3.8)

то условие (3.6) означает всего лишь равенство их угловых коэффициентов

(1 + A / ю о, ²) = (1 + B / ю о² ) ^{- 1}.                                           (3.9)

Мы видим, таким образом, что традиционная постановка задачи о Ф-Б неустойчивости фактически приводит к одному уравнению относительно двух переменных n e и n i . liyoiio eg (3.5) можно установить только связь между спектрами концентраций электронов и ионов (3.8), но нельзя найти их конкретные выражения. Для получения конкретных выражений n_e ( ю, к ) и n i ( ю, к ) задачу о Ф-Б неустойчивости следует формулировать в иной, более общей постановке.

• 4.    Более общая постановка задачи

Решения системы дифференциальных уравнений (2.1) обретают определенность лишь тогда, когда заданы самосогласованные начальные условия для всех ее переменных. Чтобы упростить задание самосогласованных начальных условий, предположим, что в начальный момент времени t = 0 в плазме возникла какая то неоднородность n (r) с одинаковыми концентрациями электронов и ионов n (r) = ne (r) = n (r).

(4.1)

В такой неоднородности электрическое поле E ( r ) в момент t = 0 будет равно нулю, и, соответственно, равны нулю порождаемые им скорости электронов и ионов ( V e ( r ) = V ( r ) = 0). Это позволяет нам ограничиться заданием только одного начального условия (4.1).

Введение начального условия в систему уравнений (3.4) проще всего осуществляется с помощью одностороннего преобразования Лапласа по переменной t . Записав (2.2) в виде а + j оо   о

S (r, t) = (2 п j)-1 | dp J S (p, к) exp (pt - jkr) dk а - j о - о и учитывая, что преобразование Лапласа от производной по времени имеет вид дne,i / дt = pnei - n(0, к), получим вместо (3.5) систему двух неоднородных уравнений

(юо i2 + A) ni (p, к) - ю о i2 ne (p, к) = (p + Vi) n (0, к), - юо i2 ni (p, к) + (юо i2 + B) ne (p, к) = Vi R-1 n (0, к), в которых частота ю заменена на ю = -jp, т.е. A и B а (3.4) имеют вид

A = p (p + v i ) + k ² V t i ²

(4.3)

(4.4)

B = v i R ^{- 1} (p - j к V e о ) + k ² V t , ².

Решения системы (4.2) записываются в виде ni (p, к) = n (0, к) [(p + vi) (1 + B / ю оi2) + viR-1] / (A + B + A B / ю о,2)

ne (p, к) = n (0, к) [v R-1 (1 + A / юо i2) + (p + vi)] / (A + B + A B / юо,2), т.е., в отличие от (3.8), мы получаем конкретные выражения для ne(p, к) и ni(p, к).

Полагая, как и в предыдущем случае, B / ю _0i ² ~ A / ю _0i ² <<  1 и пренебрегая AB / ю _0i ² по сравнению с A + B , можно, учитывая квазинейтральность неоднородности, записать

Пе (p, k) ® n (p, k) ® n (0, k) [p + Vi (1 + R) / R] / (A + B).(4.5)

Корни уравнения A + B = 0 здесь аналогичны корням (3.7), т.е. совпадают с корнями (2.15-2.17):

pi = уi + j Qi» — R [V (1 + R)]-1 { к2 Vs2 — [ k Ve о / (1 + R) ]2} + j k Ve о / (1 + R)(4.6)

Р2 = У2 + j ^2 ” - [V (1 + R)] / R + j k Ve 01 (1 + R).(4.7)

Зная эти корни, можно по теореме о вычетах сразу записать зависимость пространственного спектра концентрации (4.5) от времени t

П е, i ( k , t ) = n (0, k ) {[ p i + V (1 + R ) R ^{- 1} ]( Р 1 - Р 2 ) ^{- 1} exp( p i t ) + [p 2 + V i (1 + R ) R ^{- 1}]( p 2 - p i ) ^{- 1} exp p t )}.

Подставив сюда p 1 и p₂ из (4.6), (4.7) и учитывая, что V i (1+ R ) R ^{- 1} >>  Q >>  y 1 , получим для интересующего нас корня (4.6)

n e,i ( k , t ) ® n (0, k ) exp ( y i t + j Q i t ).                                       (4.8)

Для завершения конкретизации (4.8) нужно задать начальную форму неоднородности (4.1) и найти ее пространственный спектр n ( k , 0). Сделаем простое предположение о том, что начальная неоднородность изотропна и в точке r = 0 имеет единственный максимум

n(r) / NN = n1 (r), где n1 (0) = 1. Тогда, записав n1 (r) в виде n1 (r) = exp [ln n1 (r)] и разложив ln n1 (r) в ряд Маклорена, получим n (r) = AN exp {[n1 ‘(0) / n1 (0)] r + [n1 ‘‘(0) / 2 n1 (0)] r2 + ...}.

Поскольку первая производная n1' в точке максимума равна нулю, а вторая производная n1 ‘‘ в этой точке отрицательна, то, ограничившись квадратичным членом, придем к выражению n (r) = AN exp (- r2 / T2), в котором T 2 = 2/n‘‘(0). Иными словами, любую изотропную неоднородность с одним максимумом можно в первом приближении считать гауссоидом. Пространственный спектр гауссоида имеет вид n (к) = п3/2 AN T3 exp (- к2 T2 / 4), или в более компактной форме n (к) = f (0) exp (- к2 T2 / 4),                                   (4.9)

где f0) = п3/2 AN T3.                           (4.10)

Подстановка (4.9) в (4.8) с учетом (4.6) приводит к конкретному выражению для зависимости пространственного спектра исходной неоднородности от времени t nei(k, t) = f0) exp{(-к2T2 / 4) - [R / v(1+R)] [к2 Vs2 - [V / (1+R) ]2] t + j kVeot / (1+R)}.        (4.11)

Физический смысл этого выражения обсуждается в следующем разделе.

• 5.    Эволюция пространственного спектра неоднородности

Рассмотрим вначале эволюцию спектра (4.11) с позиций букеровской модели образования авроральных неоднородностей. Напомним, что в ней фигурируют неподвижные неоднородности, дрейфовая скорость которых Ve0 = 0. Амплитуду спектра (4.11) в этом случае можно записать в виде ne, i(k, t) = f0) exp (-к2 Tm2 / 4),                                        (5.1)

где

T экв ² = T ² + 4 [ R V s ² / V i (1 + R )] t .                               (5.2)

Эквивалентный размер неоднородности T э _кв с течением времени t здесь увеличивается, но скорость его увеличения различна для разных направлений. Это связано со специфической зависимостью параметра R (2.11) от ракурсного угла V . При ориентации волнового вектора k вдоль магнитной силовой линии ( V = 90 ° ) этот параметр имеет величину

R = ®H е Vi / ®Hi Ve >> 1(5.3)

и (5.2) приобретает вид                     Tэкв2 = T2 + 4 (VS2 / Vi) t.(5.4)

При ориентации вектора k перпендикулярно магнитной силовой линии ( V = 0 ° ) параметр R равен R = V i

Ve / Юнi Юн е ~ 0.01(5.5)

и (5.2) записывается в виде       Tэкв2 = T2 + (R VS2 / Vi) t« T2 + 0.04 (VS2 / Vi) t.(5.6)

Своеобразная зависимость R от V приводит к тому, что исходная изотропная неоднородность (4.9) с течением t превращается в анизотропную, вытянутую вдоль магнитной силовой линии.

Нас в данном случае будет интересовать зависимость спектра (5.1) от t в поперечном направлении, т.е. при Т экв , определяемом выражением (5.6). На рис. 2а показаны спектры для двух начальных размеров неоднородности T = 21 и T = 0.11 в момент t = 0. Видно что при T = 21 гармоники спектра для больших волновых чисел к имеют исчезающе малую величину (например, при к = 10, n e (10.0) ~ f( 0) 3.7 - 10 ^{- 44}), и отражения от них обычным локатором регистрироваться не могут. В другом случае T =0.11 величина гармоники при том же к = 10 составляет n e (10.0) ~ f( 0) 0.78, т.е. локатор здесь способен зарегистрировать отраженный сигнал. Поскольку при любых t >  0 размер неоднородности (5.6) увеличивается, а ширина спектра (5.1) уменьшается, то становится понятным основное требование букеровской модели: исходный размер неоднородности T в момент t = 0 должен быть меньше 0.1 1.

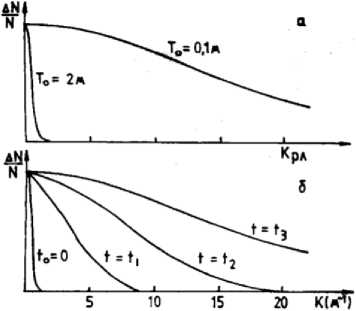
Рис. 2.     Пространственные    спектры авроральных неоднородностей.

а) Начальные       спектры       двух неоднородностей с размерами T0 = 2 м и T0 = 0,1 м в букеровской модели;

б) Эволюция спектра неоднородности с начальным размером T 0 = 2 м при

В более общем случае движущейся неоднородности (0 < V_e0 < V S ) эквивалентный размер (5.2) записывается в виде

T экв ² = T ² + 4 [ RV s ² / v i (1+ R )] [1- S ²cos² ф / (1+ R )²] t , (5.7) где S = V eo / V s и cos ф = к V eo / к V eo .

Из (5.7) видно, что в двух направлениях - вдоль магнитной силовой линии ( V = 90 ° ) и перпендикулярно вектору V_{e 0} ( V = 0 ° , ф = 90 ° ) - эквивалентный размер неоднородности увеличивается по тем же законам (5.4) и (5.6). Но в направлении вектора V_{e 0} , т.е. при V = 0 ° и ф = 0 ° , скорость увеличения эквивалентного размера уменьшается по сравнению с (5.6)

T экв ² = T ² + 4 [ R V s ² / V i (1 + R )] [1 - S ² / (1 + R )² ] t . (5.8) Это приводит к тому, что из исходной изотропной неоднородности (4.9) формируется неоднородность не с двумерной, а трехмерной анизотропией.

Принципиально иная ситуация возникает в том случае, когда S2 / (1+R)2 > 1, т.е. когда выполняется условие (2.18) развития Ф-Б неустойчивости. Эквивалентный размер (5.8) в этом случае будет с течением t не увеличиваться, а развитии Ф-Б неустойчивости. В момент уменьшаться t3 спектр совпадает с букеровским при To = 0,1 м

Tэкв2 = T2 - 4 [R Vs2 / (1 + R)] {[S2 / (1 + R)2] - 1} t, что приведет к уширению исходного спектра в направлении вдоль вектора Ve0. На рис. 2б показана эволюция такого спектра при T = 2 1, S = 2, R = 0.01, VS = 330 1п 1, vi = 103 п 1. Видно, что в момент t3 = 0.3 п этот спектр становится таким же, как спектр на рис. 2а при T =

0.1 1.

• 6.    Выводы

• 7.    Приложение

Если в букеровской модели отказаться от рассмотрения неподвижных неоднородностей и перейти к рассмотрению неоднородностей, движущихся со скоростью V_eo / V_S >  1, то в ней сразу же исчезнет проблема чрезвычайно малого размера исходной неоднородности T mm <  0.11, которую в свое время не смог преодолеть Букер. Начальный размер неоднородности Т в этой более общей модели может составлять несколько метров, а необходимый минимальный размер T mm < 0.1 1 достигается за счет развития Ф-Б неустойчивости.

Вместе с тем в этой более общей модели сохраняет свою справедливость главный вывод Букера о непригодности тепловых флуктуаций для формирования авроральных неоднородностей. В самом деле, из (4.11) видно, что Ф-Б неустойчивость развивается не в самой плазме, а в ее отдельных неоднородностях. Мы уже говорили, что любую неоднородность, порожденную тепловыми флуктуациями, можно разложить в пространственный спектр п _теп( к ). Но этот спектр существует столько времени, сколько существует сама неоднородность. Поскольку время жизни тепловых неоднородностей чрезвычайно мало (t_m ~ 10 ^{- 7} п), то за это время их размеры (5.4), (5.6) и (5.7) не могут сколько-нибудь заметно измениться. Иными словами тепловые флуктуации не способны реагировать на Ф-Б неустойчивость. Поэтому схематическая картина ее развития, изображенная на рис. 1, в действительности не реализуема.

Для формирования авроральных неоднородностей нужны другие долгоживущие мелкомасштабные неоднородности, процесс эволюции спектра которых протекает так, как изображено на рис. 2б. Букер справедливо полагал, что такие неоднородности могут возникать на высотах Е-области полярной ионосферы только в результате турбулентного распада крупномасштабных неоднородностей.

Чтобы преобразовать скалярно-векторное произведение к виду

k(Ve × H0 / H0) = ωHe νe-1 k Ve / (1 + ωHe2 νe-2 sin2 Ψ),(П.1)

ориентируем вектор H 0 вдоль оси Z . Тогда векторное произведение запишется в виде

Ve × H0 / H0 = Ve b = Vey i - Vex l,(П.2)

где i, l и b - орты декартовой системы координат. Скалярное умножение (П.2) на k дает k (Ve × H0 / H0) = kx Vey - ky Vex.(П.3)

Чтобы преобразовать правую часть (П.3) к форме (П.1), умножим исходное уравнение (2.3) векторно на k . Поскольку продольные плоские плазменные волны можно с хорошим приближением ( Гершман и др ., 1976) считать потенциальными ( k || E ), то, положив k × E = 0, получим из (2.3)

ν e k × V e + ω H e ( k × V e × H 0 / H 0 ) = 0.

Подставив в это уравнение k × Ve × H0 / H0 = Ve (k H0 / H0) - (k Ve) H0 / H0 = Vex kz i + Ve y kz l - (Ve x kx + Ve y ky) b, k × Ve = (ky Ve z - kz Ve y) i + (kz Vex - kx Ve z) l + (kx Ve y - ky Ve x) b, получим систему трех уравнений

ωH e νe  Ve x kz = - (ky Ve z - kz Ve y),(

ωH e νe  Ve y kz = - (kz Vex - kx Ve z),(П.5)

ωH e νe  (kx Ve x + ky Ve y) = kx Ve y - ky Ve x.(П.6)

Если в левую часть (П.6) добавить и отнять k_z V_ez , то его можно переписать в виде

ωH e νe k Ve - ωH e νe  kz Vez = kx Ve y - ky Ve x.(П.7)

Задача в этом случае сводится к нахождению выражения для k z V ez . Найдем V ex и V ey из (П.4) и (П.5)

V ex = V ez ( k x - ω He ν e ^{- 1} k y ) / k z (1 + ω He ² ν e ^{- 2}),

V_ey = V_ez ( ω _He ν _e  k_x + k_y ) / k_z (1 + ω _He ν _e )

и подставим их в левую часть (П.6)

ω _{H e} ν _e ^{- 1} V_ez [( k_x ² + k_y ² ) / k_z (1 + ω _{H e} ² ν _e ^{- 2} )] = k_x V_{e y} - k_y V_{e x} .

Отсюда следует ω H e ν e ^{- 1} k z V ez = ( k x V e y - k y V e x ) k z ² ( k x ² + k y ² ) ^{- 1}(1 + ω H e ² ν e ^{- 2}).

Учитывая, что ω _He ² ν _e ^{- 2} >>  1 и k_x = k cos Ψ cos ϕ , k_y = cos Ψ sin ϕ , k_z = k sin Ψ , получим для небольших Ψ

ω _{H e} ν _e k_z V_ez = ( k_x V_{e y} - k_y V_{e x} ) ω _{H e} ν _e tg Ψ ≈ ( k_x V_{e y} - k_y V_{e x} ) ω _{H e} ν _e  sin Ψ .

Подстановка этого выражения в (П.7) дает kx Ve y - ky Ve x = ωH e νe-1 k Ve / (1 + ωH e2 νe-2 sin2 Ψ)

или с учетом (П.3) - выражение (П.1).

Работа выполнена при частичной финансовой поддержки РФФИ (грант № 98-05-64144).