Автодинная интерферометрия расстояния с помощью полупроводникового лазера при токовой модуляции длины волны излучения

В работах [1, 2] приведено обоснование возможности успешного использования лазерных методов, основанных на токовой модуляции лазерного излучения, для определения расстояния до объекта. Применение полупроводниковых лазеров в качестве перестраиваемых источников когерентного излучения открывает возможности создания малогабаритных измерительных систем. Одним из вариантов таких измерителей являются полупроводниковые лазерные автодинные интерферометры с оптической обратной связью [3, 4]. С помощью таких устройств можно решать задачи определения характеристик нановибраций и микросмещений, расстояния до объекта, скорости и ускорения, в том числе с использованием токовой модуляции излучения полупроводникового лазера [5–8].

Одним из параметров, влияющих на вид автодин-ного сигнала, является уровень внешней оптической обратной связи. В автодинной системе режим, при котором автодинный сигнал аналогичен интерференционному с развязкой от источника излучения, возможен при низких уровнях обратной связи [9–11].

В [2, 5, 6] описано применение пилообразной токовой модуляции длины волны излучения полупроводникового лазера. Изменение длины волны лазера Δλ всего на 0,003 нм позволяет изменять фазу отражённого от объекта излучения на 2 радиан на расстоянии более 10 см.

В [12] было предложено использовать метод измерения расстояния, основанный на использовании модуляции длины волны лазерного излучения по гармоническому закону. Целью настоящей работы явился сравнительный анализ методов измерения расстояния с помощью полупроводникового лазера при этих различных типах токовой модуляции длины волны излучения.

• 1 . Метод, основанный на использовании пилообразной модуляции излучения лазерного автодина

Излучение лазерного автодина направляется на измеряемый объект, а часть отражённого излучения попадает в резонатор полупроводникового лазера, где оно интерферирует с исходным излучением. В силу конечности скорости света отражённое излучение приходит в резонатор лазера с задержкой по времени. Изменение мощности излучения лазерного диода фиксируется с обратной стороны резонатора лазера с помощью встроенного лавинного фотодиода. При изменении тока накачки полупроводникового лазера по пилообразному закону изменяется фаза отражённого от объекта излучения, что приводит к изменению его мощности. Благодаря этому при неподвижном объекте интерференция излучений приводит к тому, что выходной ток фотодиода периодически изменяется с частотой, определяемой модуляционной характеристикой лазерного диода и расстоянием до объекта. Сигнал с фотодетектора приобретает вид высокоамплитудной треугольной составляющей за счёт пилообразной токовой модуляции лазерного диода с наложенной на неё низкоамплитудной фазовой модуляцией, формируемой за счёт изменения фазы отражённого от объекта лазерного излучения.

На рис. 1 приведён смоделированный автодинный сигнал при изменении длины волны излучения лазера Δλ = 0,003 нм, расстоянии до объекта, равном 40 см, и уровне обратной связи С << 1.

Расстояние до объекта в случае пилообразной модуляции определяется соотношением:

L =

_λ 2 N , 2 ⋅∆λ

где L – расстояние от излучателя до объекта; N – количество пиков автодинного сигнала на участке подъёма или спада; λ – длина волны излучения лазера; Δλ – изменение длины волны на одном периоде.

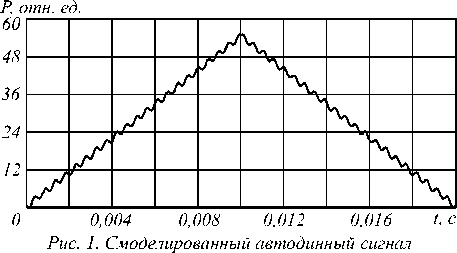
при изменении длины волны излучения лазера ∆λ = 0,003 нм и заданном расстоянии 40 см

максимальной гармоники спектра автодинного сигнала f_up . Наличие сателлитов объясняется нецелым количеством интерференционных максимумов, укладывающихся на линейном участке изменения тока лазерного диода. Таким образом, одна и та же частота с максимальной амплитудой в спектре автодинного сигнала будет соответствовать некоторому диапазону расстояний, который и определяет погрешность метода.

Результаты компьютерного моделирования для различных заданных расстояний, а также погрешность определения расстояния по модельному спектру авто-динного сигнала в процентах показана в табл. 1.

Расстояние можно также определить с помощью так называемой частоты биения автодинного сигнала, используя соотношение [4, 5]:

L =

X ² 4(d X /d t )

( f p + L . ),

где f up – частота подъема, а f down – частота спада полученного сигнала. При использовании симметричной пилообразной токовой модуляции (рис. 1), при которой время нарастания и убывания амплитуды тока выбирают одинаковыми, автодинный сигнал приобретает симметричный вид на участках подъёма и спада, и соотношение (2) при f_up = f_down принимает вид:

L = 4(d x /d 7 )² f-                             ⁽³⁾

На рис. 2 приведён спектр автодинного сигнала, изображённого на рис. 1. На низких частотах наблюдается спектр линейного нарастания или убывания пилообразной составляющей автодинного сигнала. На высоких частотах (более 200 Гц) наблюдается спектр гармонической модуляционной составляющей автодинного сигнала. В этой части спектра отчётливо выделяется частота автодинного сигнала с наибольшей амплитудой, соответствующая частоте f up .

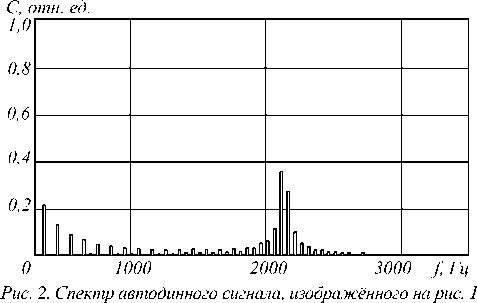
Как видно из рис. 2, при токовой модуляции длины волны лазерного излучения частота интерференционных максимумов может быть измерена с точностью, определяемой расстоянием до ближайшего сателлита

Табл. 1. Погрешность определения расстояния при пилообразной модуляции излучения лазерного автодина

Заданное расстояние до объекта, м	Рассчитанное расстояние до объекта, м	Погрешность, %
0,1	0,093	7,1
0,2	0,190	5,1
0,3	0,294	1,8
0,4	0,406	1,5
0,5	0,494	1,1
0,6	0,605	0,9

Как видно из результатов, приведённых в табл. 1, данный метод с точностью до 1,1 процента позволяет определять расстояние при значениях заданного расстояния более 50 см. При меньших расстояниях до объекта погрешность определения расстояния при пилообразной токовой модуляции возрастает до 7%.

2. Метод, основанный на использовании гармонической модуляции излучения лазерного автодина

При гармонической модуляции тока накачки полупроводникового лазерного автодина, как и в предыдущем случае, сигнал с фотодетектора приобретает вид высокоамплитудной гармонической составляющей за счёт токовой модуляции лазерного диода с наложенной на неё низкоамплитудной фазовой модуляцией, формируемой за счёт изменения фазы отражённого от объекта лазерного излучения. При воздействии отражённого излучения от объекта на лазерный диод излучаемая им мощность может быть определена в результате использования малосигнального анализа дифференциальных уравнений для комплексного электрического поля с запаздывающим аргументом и концентрации носителей заряда и записана в виде [12]:

P ( j ( t )) = P( j ( t )) + P 2 cos ( W( j ( t )) T o ( t )) ,         (4)

где P 1 ( j ( t )) – составляющая мощности, не зависящая от расстояния до внешнего отражателя, P 2 – амплитудная составляющая мощности, зависящая от фазового набега волны ω( j ( t ))τ₀( t ) в системе с внешним отражателем, τ ₀ – время обхода лазерным излучением расстояния до внешнего отражателя, ω( j ( t )) – частота излучения полупроводникового лазера, зависящая от плотности тока накачки j ( t ) и уровня обратной связи.

При модуляции длины волны излучения полупроводникового лазера частота и амплитудная составляющая мощности излучения лазера определяются соотношениями:

и ( j ( t )) = и ₀ + ® A sin(2 nv 1 t ) ,

Pi(j(t)) = 11 sin(2nvit), где ω0 – собственная частота излучения полупроводникового лазерного диода; ωA – девиация частоты излучения полупроводникового лазерного диода; ν1 – частота модуляции тока питания лазерного диода, I1 – амплитуда токовой модуляции составляющей P1( j(t)).

Таким образом, выражение для мощности излучения частотномодулированного полупроводникового лазера (4) запишется в виде:

P ( j ( t ) ) = 1 1 sin(2 nv i t ) +

+ P ₂ cos ( и ₀ t ₀ + to A T ₀ sin (2 nv 1 t )),

где стационарная фаза автодинного сигнала θ = ω0τ0, амплитуда фазы токовой модуляции σ = ωAτ0, круговая частота модуляции тока питания лазерного диода Ω = 2πν1.

Для описания низкочастотного спектра автодинно-го сигнала при гармонической модуляции длины волны излучения лазерного диода мощность автодинного сигнала может быть представлена в виде разложений в ряд по функциям Бесселя первого рода J n :

P ( t ) = 1 1 sin ( Q t ) + P ₂ cos ( 0 ) J 0 ( G ) +

+ 2 P ₂ cos ( 0 ) • £ J _{2 n} ( G ) • cos (2 n • ( Q t )) -             (6)

n = 1

M

-2P2 sin (0) • £ J2n-1 (G) • sin ((2n - 1)(Q t)), n=1

и в ряд Фурье с коэффициентами разложения a n и b n :

P ( t ) = a 0 /2 + £ ( a _{2 n} cos (2 n Q t ) - b_2n sin (2 n Q t )) + n = 1

+ E ( a 2 n —1 cos((2 n —1) Q t ) - b _{2 n} —1 sin(2 n -1) Q t )).

n = 1

Из равенства соотношений (6) и (7) можно записать выражения для амплитуд спектральных гармоник Фурье-спектра S_n , соответствующих амплитудам спектральных составляющих разложения в ряд по функциям Бесселя.

Вводя коэффициенты C n , равные по модулю чётным и нечётным спектральным составляющим разложения ряда Фурье и определяемые как

^S 2 n = V a 2 n ^{+ Ь} 2 n , ^S 2 n + 1

V a 2 n + 1 ^{+ b} 2 n + 1

выражения для амплитуд спектральных гармоник Фурье-спектра S n и S 2 n +1 , за исключением случая n = 1 для нечётных гармоник, будут иметь вид

S 2 n = 2cos( 0 ) • P 2 • J 2 n ( G ),                            (9)

S 2 n + 1 =- 2sin( 0 ) • P 2 • J 2 n + 1 ( G ).                      (10)

Моделирование автодинного сигнала с использованием данного метода проводилось при параметрах:

λ = 650 нм, амплитуда отклонения частоты излучения полупроводникового лазерного диода to А = 10¹⁰ рад/с. На рис. 3 представлена зависимость мощности излучения лазерного автодина от времени при расстоянии до объекта 40 см, а на рис. 4 – его спектр при уровне обратной связи С << 1.

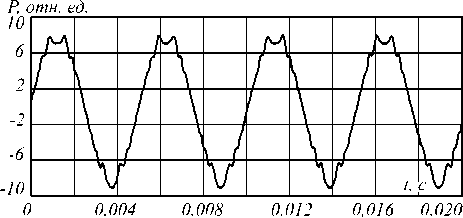
Рис. 3. Зависимость мощности излучения лазерного диода от времени

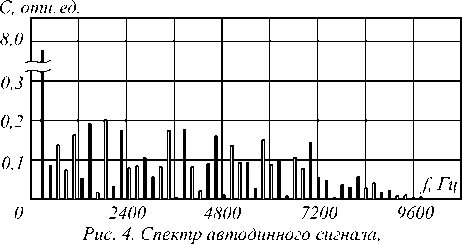
изображённого на рис. 3

Для определения расстояния до объекта L , входящего в параметр σ, используем отношение для 2 n и 2 n +2 и отношение для 2 n + 1 и 2 n + 3 спектральных гармоник:

S 2 n = J 2 n (^G) , S 2 n + 2 J 2 n + 2 ( G )

S 2 n + 1 = J 2 n + 1 ^(g)

S 2 n + 3     J 2 n + 3 ( G )

Решение полученных уравнений (11) и (12) относительно неизвестного параметра σ = ω A τ 0 требует знания параметров токовой модуляции лазерного автодина, в частности, девиации частоты излучения лазерного диода ω _A . Принимая во внимание, что τ ₀ = 2· L / c , получаем соотношение для определения расстояния до объекта:

L = C •— . (13)

• 2    to A

Как видно из рис. 4, спектр автодинного сигнала при гармонической токовой модуляции имеет более сложный характер по сравнению со спектром авто-динного сигнала при пилообразной токовой модуляции. Это обусловлено тем, что изменение фазы в методе гармонической токовой модуляции длины волны лазерного излучения происходит неравномерно, с изменяющейся частотой, формируемой из-за изменения длины волны лазерного излучения с переменной скоростью. Частоты спектральных составляющих авто- динного сигнала оказываются кратными частоте токовой модуляции. Поэтому для определения расстояния до отражателя используются амплитуды спектральных составляющих автодинного сигнала.

На измерение величины расстояния до отражателя будет существенным образом влиять точность определения амплитуд спектральных составляющих авто-динного сигнала, которая, в свою очередь, зависит от зашумлённости автодинного сигнала.

Компьютерное моделирование погрешности определения расстояния до объекта в методе с гармонической модуляцией длины волны лазерного излучения проводилось при различных расстояниях с учётом влияния шумов измерительной системы на амплитуды спектральных составляющих, входящих в соотношения (11) и (12). В расчётах задавалась 10% величина шумовой составляющей, накладываемой на моделируемый автодинный сигнал, на разных расстояниях от излучателя до отражателя. Результаты расчёта средней погрешности для различных расстояний представлены в табл. 2.

Табл. 2. Погрешность определения расстояния при гармонической модуляции излучения лазерного автодина

Заданное расстояние до объекта, м	Рассчитанное расстояние до объекта, м	Погрешность, %
0,1	0,1035	3,55
0,2	0,1957	2,17
0,3	0,2949	1,70
0,4	0,4054	1,35
0,5	0,5066	1,32
0,6	0,6079	1,33

На рис. 5 приведена зависимость средней погрешности определения расстояния до объекта при различных значениях для двух методов токовой модуля-

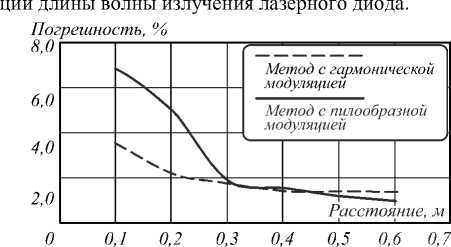
Рис. 5. Зависимость средней погрешности от измеряемого расстояния для двух методов токовой модуляции длины волны излучения лазерного диода

Заключение

Результаты компьютерного моделирования показали, что погрешность определения расстояния в методе с гармонической модуляцией уменьшается с увеличением расстояния до измеряемого объекта, однако при небольших расстояниях её величина значительно меньше, чем в методе определения расстояния при пилообразной модуляции длины волны лазерного излучения.

На рис. 5 наглядно показано, что погрешность при малых расстояниях в методе с пилообразной модуляцией тока более чем в два раза больше, чем в методе с гармонической токовой модуляцией. На расстояниях от 30 см до 50 см точность обоих методов практически идентична. С увеличением расстояния погрешность метода с пилообразной модуляцией становится меньше, чем у метода с гармонической модуляцией. Последнее объясняется тем, что при измерениях амплитуд спектральных составляющих с увеличением их числа точность не увеличивается, а при измерениях частоты количество периодов повышает точность измерений.

Таким образом, при измерениях расстояний до 30 см более высокую точность обеспечивает метод с гармонической токовой модуляцией, а при измерениях расстояний, больших 50 см, более высокую точность даёт метод с пилообразной токовой модуляцией.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ (государственное задание №8.7628.2017).