Автоколебания газа, вызванные теплотой сгорания топлива или конвективным теплоподводом

В распределенных системах гидродинамического типа ламинарно-турбулентный переход, в частности возбуждение автоколебаний, исследуется с ростом числа Рейнольдса, как правило, обусловленного увеличением средней скорости потока. В данных исследованиях одним из основных инструментом является привлечение различных бифуркационных теорем, например теоремы Андронова–Хопфа о бифуркации рождения цикла.

Отметим, что рост числа Рейнольдса может быть обусловлен также и падением вязкости, что имеет место при определенных движениях многофазных сред, структурированных и стратифицированных жидкостей, а также при подводе теплоты к жидкости или теплоотводе от нее. В жидкостях с сильной зависимостью вязкости от температуры при достаточных градиентах давления возникает явление саморазогрева, также приводящее к падению вязкости. Дестабилизирующая роль вязкости является следствием закона запаздывания в передаче действия в вязкой среде, а это запаздывание может изменить знак эффективного трения, т.е. вызвать неустойчивость. В [1] рассматривается образование отрицательного сопротивления и автоколебаний в потоке жидкости с экспоненциальной зависимостью ее вязкости от температуры, причиной которых является ее саморазогрев. В монографии [2], авторы которой провели значительное число экспериментальных исследований феномена Рийке, утверждается, что классическая модель волновых процессов не может объяснить причины самовозбуждения автоколебаний. В [3] был обоснован механизм отрицательного сопротивления на зависимости гидравлических потерь по длине трубы Рийке при постоянном тепловом потоке. Применение этого механизма позволило определить теоретически закономерности феномена Рийке [4]. Теоретическое описание феномена Рийке, в основу которого положены механизмы отрицательных сопротивлений, качественно и количественно подтверждаются результатами экспериментов [2].

По-видимому, впервые в монографии (см. с. 180 [5]) было установлено, что процесс подвода тепла вносит в поток газа особый вид сопротивления: при подогреве движущегося газа полное давление падает. Обнаруженное сопротивление Г. Н. Абрамовичем было названо «тепловым» и в [5] приведено его термодинамическое истолкование. В монографии [6] Б. В. Раушенбах получил выражение для теплового сопротивления при нагреве идеальной (невязкой) несжимаемой жидкости и привел его обоснование как механизма возбуждения вибрационного горения. С помощью полученного в [6] соотношения для теплового сопротивления Б. В. Раушенбах пытался представить качественную картину возбуждения акустических колебаний теплоподводом за счет кинетической энергии течения. Было высказано, что если теплоподвод будет колебаться около нуля, то на поток будет попеременно действовать то положительное, то отрицательное сопротивление. Если при этом увеличению скорости течения будет соответствовать уменьшение сопротивления, то система будет раскачиваться (см. с. 81 [6]).

Согласно общим представлениям механики [7] эффект «отрицательного» сопротивления или «отрицательного» трения состоит в реализации условий, когда с увеличением скорости движения механической системы ее энергия не уменьшается (например за счет сил вязкого трения, пропорциональных скорости), а, наоборот, увеличивается. Физика такого явления в различных системах своя. Однако благодаря данному явлению установившееся движение (или положение равновесия механической системы) становится неустойчивым и в системе возможно самовозбуждение автоколебаний.

Таким образом, «отрицательное» тепловое сопротивление – это формальный термин, означающий, что при выполнении определенных условий местное гидравлическое сопротивление зоны теплоподвода не возрастает с увеличением скорости движения теплоносителя, а, наоборот, уменьшается, что приводит к возникновению гидродинамической неустойчивости и возбуждению автоколебаний.

В [8] получено выражение для теплового сопротивления, возникающего при политропном подводе теплоты к одномерному движущемуся совершенному невязкому газу.

В данной работе, исходя из фундаментальных законов сохранения механики сплошной среды и базовых уравнений термодинамики, рассмотрена задача получения общего уравнения для тензора диссипации тепловой энергии, возникающего при локальном тепло-подводе к трехмерному потоку газа. В частном случае одномерного потока данный тензор вырождается в рассмотренное ранее тепловое сопротивление.

• 2.    Вывод уравнений движения при теплоподводе

Рассмотрим движение вязкой теплопроводящей сжимаемой жидкости (рис. 1) с локальным теплоподводом, распределенным вдоль некоторой поверхности X . Выделим в потоке движущейся среды в начальный момент времени t о малую область Q _t 0 , составленную из частиц среды. Тогда в момент времени t>t 0 данная область (рис. 1), деформируясь, перейдет в некоторую область Q t . Непосредственным вычислением можно проверить справедливость следующего интегрального равенства:

Ш a ^ ) d"

Q t

jjj ^ + Ц а ⁽rt ) ( V-n) Q t             d Q t

ds,

где a (r, t) — произвольная достаточно гладкая скалярная, векторная или в общем случае —      — тензорная величина, dw = dx 1 dx2 dx3 - элемент объема физического пространства, V (r, t) - скорость движения жидкости в момент времени t в точке, определяемой радиус-вектором r, n - внешняя нормаль к поверхности дQt, а ds — элемент ее площади.

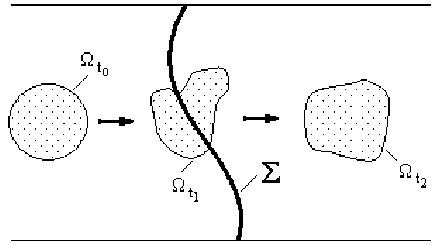
Рис. 1. Схематическое выделение в потоке среды «жидкого объема» Q t

Полагая в тождестве (1) a = p ( r ,t ) - плотность среды и используя формулу Гаусса-Остраградского:

Ң p ( r ,t ) ( V • n ) ds = JJJ div ( pV ) du,

д Q t

Q t

получаем тождество

djp n )-=f в

+ div ( pV )

dω.

Q t

Q t

В рассматриваемой задаче нет внутренних источников производства или поглощения массы. Поэтому из закона сохранения массы следует, что ddtjffp (n’t)du=0 ’

Qt и, следовательно, из (2) получается обычное уравнение неразрывности

^ + div ( pV ) =0 .

∂t

Таким образом, уравнение неразрывности (3) эквивалентно следующему, используемому нами далее уравнению, выражающему закон сохранения массы в балансной интегральной форме:

f ^ + L(ⁿ ’t ) V . n> = 0 .

Q t             д Q t

Для вывода уравнения движения поступаем следующим образом. Применяем второй закон Ньютона к подвижному «жидкому» объему Qt, рассматривая его как материальное тело, а оставшуюся часть жидкости – как действующие на него внешние силы, обусловленные вязкостью и статическим давлением. Имеем d Ш pV (r’t) d^ = Ш P (n,t) gd^ + ]J T ‘ nds + JJJ 5E (r — r^) Tт ■ nsd^,

Q t

Q t

д Q t

Q t

n

n

где g - вектор ускорения свободного падения, т - тензор напряжения, тт - тензор диссипации тепловой энергии, 5^ (r — r^) - дельта-функция Дирака, ассоциированная с поверх-n ностью теплоподвода X. Тензор тт действует на подвижный объем Qt лишь в случае его пересечения поверхности теплоподвода X. Таким образом, согласно определению дельтафункции δΣ, справедливо представление (рис. 1):

JJJ § s ( ^— - ^— s ) ^— г • n s dw = <

Q t

— тг (rs) • nS при Qt n X = 0, 0 при Qt П X = 0.

—

Далее, полагая в (1) a = pV и используя формулу Грина интегрирования по частям [9], получается тождество

IIP ^ > dw = f

Q t

Q t

^д f ^pV^ /—      —     —     —

-^+ + ( V • v) (pv ) + ( pv) div (v)

dω.

—    —

—    —

Введением [9] в рассмотрение изотропного тензора p ( r,t ) I , где I - еденичный тензор,

— — получим представление τ

—  —

—

— p ( r,t ) I + — , где - - неравновесный тензор напряжения

трения, который для ньютоновской жидкости в координатах имеет вид

∂υ i    ∂υ j

° ij = 4, dX j ⁺ dx ;

^^^^^^^^r

2 d„ k         d„ k

3 ij dx k)      ij dx k'

где μ – молекулярная вязкость, ξ – объемная (вторая) вязкость. Вновь воспользовавшись формулой Гаусса–Остраградского, получаем

jj ^— • nnds = — d Q t

Щ grad [ p ( r,t )] dw + HI div ( ^— } dw,

Q t

Q t

и, таким образом, уравнение движения (5) в балансной интегральной форме окончательно запишется в виде

f

Q t

^д (^pV) /—      —— —\

dw =

= Ш p ( ^—, t ) ^—dw — IJJ grad [ p ( r, t )] dw + jj! div ( ^— ) dw + IJJ § _S ( ^— — ^— e ) ^— г • n _S dw,

Q t

Q t

Q t

Q t

или в координатной дифференциальной форме

Ә ( pu i )

-эГ = ^pgi^—

^{9 (n} ik ^a ik ) + § s ( — — — e ) t i ^k n s , ∂x k                   ^т

где П ik = p& ik + pu i U k — тензор плотности потока импульса.

В силу уравнения неразрывности (3), с учетом явного вида компонент σ ij тензора пряжения трения и следующего тождества:

на-

dp i ) ∂t

+ ^ = /£ + „к ^ + U i д^ ∂x k         ∂t ∂x k         ∂t

d ( p„ k )          du ;       du; \

∂x k        ^ρ ∂t      ^k ∂x k ^,

уравнение (8) запишется в виде

∂υi     ∂υi p\"5i + Uk ax-J = pgi—

∂ ² υ k

dp + цa„; + U+0„ „ oxi                 3/ Oxi Ox к

+ § s ( ^— — ^— e ) T i ^k n s .

Отметим также, что при отсутствии теплоподвода для несжимаемой среды с постоянной плотностью р = const ( ^ согласно (3) ди к / дх к = 0 ) из последнего уравнения получается обычное уравнение Навье–Стокса для несжимаемой жидкости:

du i       du i =      1 др     ү^-' д ² u i

∂t     k ∂xk gi ρ ∂xi k=1 ∂x2k , где v = р/р - кинематическая вязкость.

В уравнении (8) остается неизвестной величина τтik, уравнение для которой нами далее будет получено как следствие закона сохранения энергии. Перейдем к составлению уравнения энергии в рассматриваемой нами задачи. Обозначим через u(г, t) - внутреннюю энергию единицы массы среды. Тогда полная энергия в объеме Qt определяется интегралом

E =

Ш р(и + ф)

dw . Полагая в тождестве (1) a = р

(и + Ф ).

получим

dE = Ш d^Au ⁺ V-)^{dw +} Л ^р(^{и +} V ") ( V • ^- ) ^ds. Q t        ^Х          д      Ә Q _t    ^{Х          7}

Выясним теперь, какую работу производят силы, действующие на рассматриваемый подвижный элемент среды Q _t . В единицу времени над данным элементом производится: JJ р ( v • nds - работа сил давления, JJ —с • n • Vds - работа сил вязко- д Q t ^х                                                д Q t ^х

го трения, JjJ р -д ■ V I Q t

—

—

dw - работа массовых сил, JJJ 5 s ( г — г s ) ( - _т • — s ) • Vdw - работа Q t

сил «расширения-сжатия» в окресности поверхности X . Когда объем Q t имеет непу-

стое пересечение с поверхностью теплоподвода X , внутрь его через каждый элемент поверхности Q _t QX в единицу времени передается теплота q ( г s , t ) . Суммируя с помощью дельта-функции δ Σ эти элементарные тепловые потоки, окончательно получим, что суммарное количество теплоты, получаемое подвижным объемом Q _t в единицу времени при прохождении им поверхности теплоподвода X , определяется следующим интегралом: JJ 5 s ( r — r _s ) q ( г, t ) dw .

Q t

Согласно закону сохранения энергии будем иметь

— H Р ( V • - ) ds + Ц ( с • n ) • Vds + д Q t                  д Q t

Ш дЛ^ ⁺ V) d ^{w +}Л ^р(^{и +} V ) ( ^- ) ^ds =

Q t        ^X          '      д Q t    ^{X          7}

+

j ^{р -} • V) d ^w+л

—-           —-

( r — r s ) ( т _r • n s ) • Vdw +

Q t

Q t

jjj 5 s ( r — r s ) q ( ^— ,t ) dw, Q t

или после преобразования с помощью формул Грина поверхностных интегралов в объемные

Q t

ри + ^р 2 ' ^ dw = ^ div ( с • V — pV ) dw +

Q t

+

Iffр —-i' ^dw+lff

Q t

Q t

δ Σ

- -

( r — r s ) ( т т • n s ) • Vdw +

jj! 5 s ( r — r s ) q ( r,t ) dw.

Q t

Последнее уравнение и выражает собой в балансной интегральной форме закон сохранения энергии для рассматриваемого случая (рис. 1). Упростим несколько это уравнение, с целью получения той его формы, в которой пишут уравнение энергии при формулировке первого начала термодинамики. Прежде всего, учитывая уравнение неразрывности (3), левую подынтегральную часть в (10) представим в виде

(д               р | V 1 ²А      ә / V 1 ² A -    / V 1 ² A

( at ⁺ d") ^ ^p“ ⁺ 2 ■   ^р* ^ ⁺ 2 i ^{+ dlv} V ⁺ 2 <

( |V 1 ² Әр         — d ( V | ²\

+р (u+ Ат) (s+dlv VH ) = ' t ^2,■ а также учитывая, что после прибавления ρ ddpρ

% = $ ^{+ V} grad ⁽ р ) ■ ^{dlv V} = - p ^ = р dp ■ р dp - ^dlv ( ? ^V ) = ж ■ к обеим частям уравнения (10), оно окончательно запишется в виде

I 4t(u ⁺ V "⁺ р^“ = I ^dlv ( ^T ' ^V ) ^d “ ⁺ I apd" ^{+        (11)}

Q t         ^{x                 7}         Q _t                         Q t

+ f р Q-v) d" + J 6 s ( T -

—     —

^T e ) ( ^— г • n s ) • Vd" +

Q t

Q t

HI 6 s ( r - r s ) q ( r,t ) d".

Q t

Из уравнения (11) получается уравнение для компонент тензора теплоподвода (дисси-— пации тепловой энергии) тг = || тГ^ || ^ к=13:

т ik n E U k = C - д ( O ik U i ) /дх к

-

ρg k υ k ,

где C = р -dt Ци + Й ² + Р^ - dp/dt - q ( r s ,t ) .

• 3.    Компоненты тензора диссипации тепловой энергии для одномерного установившегося течения невязкого газа

В предположении одномерного установившегося движения гидравлически идеального (невязкого) газа тензор диссипации тепловой энергии имеет одну компоненту τ _т ¹¹ и уравнение (12) принимает вид

∂E     τ11

= —— + — ■

∂x     ρρυ где E = и + ^22 + p и учтено, что в этом случае V(T) = и(x)Tr, T = x—r, grad = д/дх.

x2 τ11

Полагая Ahт = J -р-dx, q* = J pU dx, из (12) получаем уравнение энергии в форме 1-го x1

закона термодинамики для потока идеального газа:

E 1 + q * = E 2 + A h т ,

где A h _т - потери энергии из-за теплового сопротивления, q * - подводимый удельный тепловой поток. При политропном подводе теплоты, когда q * = c vn— l ( T 2 - T 1 ) , где c _v - удельная теплоемкость изохорного процесса, n и k – соответственно показатели политропы и адиабаты, с учетом того, что p 2 /р 2 - p 1 /р 1 = R ( T 2 - T 1 ) и R ( T 2 - T 1 ) = c v ( к - 1) ( T 2 - T 1 ) , уравнение (14) позволяет определить A h _т в таком виде:

к - 1А          m \ и2 - и" ²

A hт = n         cv (T2 - T1) +

\ 1 - n/ откуда, полагая hт = р 1Ahт, для теплового сопротивления, выраженного в единицах давления, получаем выражение [8]:

hт=пр 1 (k-n) cv(T2- T1)+^ [1- (T2)   ]•

При изобарном теплоподводе (n = 0) из (15) находим, что h т( Q) =

ρ 1 Q ²

2 S ^{1 2}

1 -

^T T ² 1 ^{2 ,}

где Q = и 1 S — объемный расход среды.

4. Граничная задача феномена Рийке

Простейшей динамической системой с локальным подводом теплоты, в которой при определенных условиях самовозбуждаются автоколебания, является труба Рийке. При рассмотрении труб достаточно малого диаметра, можно ограничиться одномерной постановкой задачи. При малых числах Маха M ^ 1 (т.е. при дозвуковых скоростях) в уравнениях движения можно пренебречь [10] конвективными слагаемыми υ ^∂ _∂ ^υ _x и υ _∂ ^∂ _x ^ρ . С учетом этого уравнения движения и неразрывности для одномерного движения реальной жидкости в вертикальной трубе постоянного диаметра d до зоны теплоподвода и после нее можно записать в следующей форме [10, 11]:

dG ( x,t )   2 £        ₂     dp ( x.t )        др ( x.t )    dG

ПГ + ^x (Re) a = ^-^x- ^{- p}g, -др- ⁺ dx = ⁰ .

где положено G = ри , X — коэффициент гидравлических потерь по длине гладкой трубы определяется в зависимости от режима движения из следующей зависимости

X (Re) = <

R . при Re С Re _kp ( ламинарный режим ) .

R31 , 24 . при Re >  Re _Kp ( турбулентный режим ) .

Рассматривая далее в трубе Рийке политропный теплоподвод с показателе м по литропы n и воспользовавшись уравнением состояния p/р = RT и соотношением с = V "RT , определяющим скорость звука с в среде с температурой T , из уравнения политропы ^р =

ρ ^ρ 0 ⁿ

получаем

dp = n [p of ^- )1 = "p = nRT = c. » % = (i^" dp

∂ρ ρ      ρ 0         ρ                  ∂t ∂ρ ∂t

1 dp c ² ∂t ^.

Таким образом, система (17) преобразуется в систему нелинейных телеграфных уравнений:

^{dG (} x. t ) ^{2 £}         ₂     ^d p        ^{1 d} p ⁽ x, t )    ^dG

+ ₇a (Re) ^G = ^-ix ^{- pg} . ₇2 -dp- + ix = ⁰ .

Разделим трубу Рийке (рис. 2) условно на две области: Q o - холодная нижняя часть трубы до электронагревателя и Q _T - нагретая верхняя часть трубы после электроспирали, которые пересекаются по поверхности теплоподвода X = Q o Q Q _T - зоне, в которой происходит нагрев потока электронагревателем. В каждой из областей Q o и Q _T движение воздуха описывается уравнениями (19), дополненными уравнением теплопереноса (уравнением энергии), которые также дополняются граничными условиями на входе и выходе из трубы Рийке, а также граничным условием в зоне теплоподвода X . Отметим, что при рассмотрении автоколебаний начальные условия несущественны, и мы их не рассматриваем.

Следовательно, окончательно приходим к следующей математической модели феномена Рийке (рис. 2):

p 2^ + ^и 2 дд   = - 52 - р 2 g^- дх , ^{( в} области ^ т ) ,

< 52 + Р2 тХ + U2 ^х = 0, dp2 = c2, где c2 = VkRT — скорость звука в области Пт, 'T + U2 Ц = X (T) §, X (T) - коэффициент температуропроводности воздуха, т (x) = A (Re) dр2 (x, t) и2Х), при x = £ p2 = pвх - p0g£, p1UI = Р 2 U 2,

при x = £ 1 <

W э = c п puS ( T - T 0 ) ,

p 1   p 2 — h т + h сетки, при x = 0 pвх - p 1 = kдрu2,

’ p 1 [ 1S ^{1 + u} 1 d i] = - % ^- p 1 g ^- 51 . ( в области П о ) . dp i + Р 1 дх + u 1 ⁸дх =0 ,pa . = c 1 ,c 1 = V kRT».

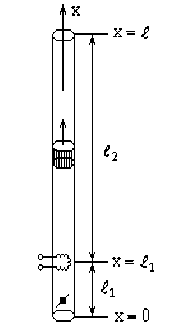
Рис. 2. Схема трубы Рийке

• 5.    Математическая модель феномена Рийке как цепочка N связанных одномерных осцилляторов

Полученную в предыдущем параграфе граничн ую зада чу (20) будем решать методом прямых (характеристик). Введем обозначения іг = 0; N - 1 , h = NN ):

G ( X i ,t ) = G i ( t ) , p ( X i ,t ) = p i ( t ) , p ( X i , t ) = p i ( t ) , T ( X i , t ) = T i ( t ) , X i = ih.

Далее заменяем дифференциальные операторы разностными:

dp I = p i +1 ⁽ t ) ^-p i ⁽ t ) + о ( һ ) , dG i Ox I_              h                     , ox I

G i ⁽ t ) —G i — 1 ⁽ t ) h

+ O ( h ) ,

дт1

dx l x = x i

P^bT-M + о (h), ■  | x x=xi

T i ( t ) - 2 T i - 1 ( t )+ T i - 2 ( t ) h ²

+ O ( h ) .

Тогда согласно (19) - (20) в области Q _T приходим к следующей системе обыкновенных дифференциальных уравнений:

' ddti + 24 X (Re) G2 = p-i^t)-      — gpi (t) , C12 dpd+l = Gi ( t ) -Gi +1( t ) , ^ i = 0; N — 1^ i                                                                          (22) dTi , Gi ГTi(t)-Ti-1(t) 1 _ (тл ГTi(t)-2Ti-1(t)+Ti-2(t) 1 dt + Pi [      h      J =x (Ti) [          h2          p pi = piRTi,Ci = nRTTi.

При каждом фиксированном значении i уравнения данной системы можно рассматривать как уравнения колебаний одномерного осциллятора. Тогда в целом вся система уравнений может быть интерпретирована как система 3 N уравнений цепочки связанных осцилляторов. Когда число таких осцилляторов стремится к бесконечности, система (22) переходит в исходную распределенную математическую модель (20) феномена Рийке в области Q _T . В нижней части трубы Рийке, т.е. в области Q q , воздух не нагретый и имеет температуру T о окружающей среды. В этой области согласно (19) - (20) движение воздуха описывается гиперболической системой, разностный аналог которой имеет вид ( г = 0; N о — 1):

^dG i    ^{2 £} 1 ,              p i ⁽ t ) ^— p i +1 ⁽ t )           ¹ dp i +1     G i ⁽ t ) ^— G i +1 ⁽ t )

— + — A (Re) G = ----- h ^{gp 0} ,       = ----- h-----,    ⁽²³⁾

где c 1 = VkRT q , k - показатель адиабаты.

Системы уравнений (22) – (23) дополняются граничными условиями и условиями в зоне электроспирали, выписанными в граничной задаче (20).

• 6.    Усреднение уравнений феномена Рийке

• 7.    Выводы

В случае малой длины £ = £ 1 + £ 2 трубы Рийке или когда достаточно ограничиться качественными соотношениями ее феномена (т.е. самовозбуждающихся автоколебаний), в полученных выше системах (22) – (23) достаточно ограничиться случаем одного осциллятора, т. е. положить N = N о = 1 . Причем из системы (22) необходимо взять лишь уравнение импульсов, а из (23) – уравнение сохранения массы. Такое усреднение исходной граничной задачи (20) приводит ее к следующей автономной диссипативной динамической системе с одной степенью свободы [3, 4]:

Ca   = Q — V (P) , La   = F (Q) — P, dt                    dt где Ca = £2c-2p-1S - акустическая гибкость трубы, La = p£2S-1 - акустическая масса нагретого столба воздуха, Q = uS - объемный расход нагретого воздуха, F (Q) = A (Q) — h^ (Q) — hт (Q) — hсетки (Q) - напорная характеристика трубы Рийке [4], A (Q) = g£2(P0 — P) - напряжение подъемной силы, h^ (Q) - вязкостные потери по длине трубы, P = p — pо, pо - давление в окружающей среде, соответственно p и p - давление и плотность воздуха в трубе Рийке, у (P) = ^P. На рис. 3 приведены зависимости для теплового сопротивления hт (Q) и вязкостных потерь h^ (Q) по длине нагретого участка трубы Рийке, а также предельный цикл и соответствующая ему форма автоколебаний давления P(t) как периодическое решение системы уравнений (24) при мощности электронагревателя Wэ = 505 кВт, и £ 1 = 1/4£, £ = 1 м, d = 0.1 м.

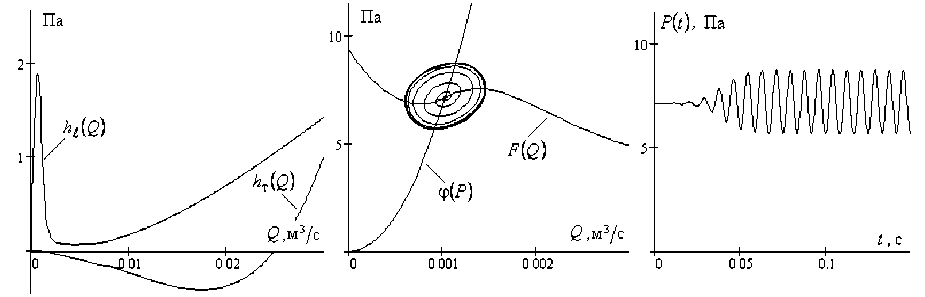
Рис. 3. Зависимости сопротивлений, предельный цикл и автоколебания в трубе Рийке

Рассмотрена задача трехмерного движения реального газа при локальном подводе к нему теплоты. Основываясь на подходе Б.В. Раушенбаха, зона теплоподвода условно аппроксимирована некоторой поверхностью, на которой терпят разрыв гидродинамические и термодинамические параметры потока газа. Вместо традиционного рассмотрения граничных условий на данной поверхности в уравнения движения с помощью обобщенной дельта-функции Дирака добавлено слагаемое в виде тензора диссипации тепловой энергии, который ассоциирован с данной поверхностью. Как следствие применения закона сохранения энергии к элементарному объему, составленному из частиц движущейся среды, получено общее уравнение для компонент тензора диссипации тепловой энергии. Рассмотрены некоторые частные случаи применения полученной общей математической модели. Для одномерного установившегося течения идеального газа тензор диссипации тепловой энергии преобразуется в тепловое сопротивление. Получена математическая модель феномена Рийке, рассматриваемая как цепочка N связанных одномерных осцилляторов. Исходя из такой интерпретации, описана процедура усреднения уравнений движения нагретого воздуха в трубе Рийке. Установлено, что ветви отрицательных сопротивлений вязкостного h e ( Q ) и теплового h _т ( Q ) при конвективном подводе теплоты в трубе Рийке составляют причину ее феномена.