Автоколебания, возбуждаемые теплоотводом от потока нагретого газа

Автоколебания в теплофизических системах, представляющие собой периодические по времени изменения гидродинамических и термодинамических параметров, являются широко распространенным явлением [1-4].

Фундаментальные исследования автоколебаний газа, в установках с источниками теплоты и массы выполнили Рэлей, Б. В. Раушенбах, М.С. Натанзон, А.Д. Марголин, С. А. Абруков, М.А. Ильгамов, В. Л. Эпштейн, К. И. Артамонов, В.Н. Подымов, В. И. Кондратьев, L. Crocco, D.T. Harrje, F.H. Reardon, H.J. Merk, A. A. Putnam, N. Rott и другие.

Неустойчивость потока, жидкости или газа, при теплоподводе или преобразовании различных форм энергии в его напор возникает во многих потенциально неустойчивых элементах теплоэнергетического оборудования. Значительные проблемы возникают перед практиками, когда, они сталкиваются с явлением возбуждения термоакустических автоколебаний

и автоколебаний вибрационного горения, возбуждающихся соответственно при конвективном теплоподводе или при сжигании топливных смесей в самых различных тепловых агрегатах - от простейших топочных устройств до камер горения воздухонагревателей доменных печей и камер сгорания мощных современных ракетных двигателей. Автоколебания давления не толвко создают большую знакопеременную механическую нагрузку на конструкцию топочного устройства, что нередко приводит к его механическому разрушению, но и изменяют условия теплообмена. В камерах сгорания, которые надежно работают в стационарном режиме, при возникновении автоколебаний резко возрастает поток теплоты в стенки, что также приводит к их термическому разрушению.

По-видимому, одна из первых авторских научных публикаций по проблеме возбуждения автоколебаний теплоподводом относится к 1859 г., когда Рийке описал ставший классическим эксперимент с трубой, получившей его имя [2]. Эксперимент был чрезвычайно прост, но не очевиден. В вертикально расположенную трубу на расстоянии четверти ее длины от нижнего основания помещалась частая сеточка. Сеточка нагревалась открытым пламенем, и, после того как пламя убиралось, возникал звук на частоте, близкой к частоте полуволнового резонанса при продольных колебаниях газа в трубе. При этом звучание продолжалось до тех пор, пока сеточка не остывала [2-3]. Несколько иначе выглядели результаты опытов тех же лет Рисса и Босша, которые помещали сеточку на расстоянии четверти длины трубы от ее верхнего основания. Автоколебания также возникали, но лишь в том случае, когда сеточка охлаждалась. В монографии [2] отмечается, что явление Рисса вполне сходно по механизму с явлением Рийке.

Если в опыте Рийке сеточка помещалась в верхней части трубы или в опытах Рисса и Босша - в нижней, то колебания не возникали. При кажущейся простоте этих опытов они до настоящего времени не имеют более или менее строгого аналитического описания, несмотря на предпринимавшиеся попытки [1-4].

Предложенный ранее механизм запаздывания сгорания топлива, предложенный Л. Крокко [3], совместно с механизмами обусловленных теплоподводом [4], проявляются в явлении «поющего» пламени Хиггинса, а также при вибрационном горении в печах и тепловых двигателях. Причем автоколебания, возбуждаемые механизмами теплоподвода, в большинстве случаев обладают диаметрально противоположными свойствами [4] в сравнении с автоколебаниями, причиной которых является запаздывание сгорания топлива.

Известно, что в ламинарном режиме движения потока причиной феномена Рийке является образование нисходящей ветви на зависимости гидравлических потерь по длине канала [5-6]. Другим механизмом данного феномена является образование «нисходящей» ветви на зависимости теплового сопротивления как функции объемного расхода воздуха [7-8]. Особенностью последнего механизма является независимость возбуждения автоколебаний от режима движения потока.

Отметим, что «нисходящие» ветви («отрицательное» сопротивление) зависимостей сопротивлений различной природы являются причиной возбуждения автоколебаний, например в электрических системах, включающих триод, при образовании вольтовой дуги, а также в различных задачах механики [9]. Однако как при теплоподводе, так и теплоотводе механизмы неустойчивости, основанные на «отрицательном» сопротивлении, оставались неизвестными.

2.    Постановка задачи

В данной работе рассматривается задача возбуждения термоакустических автоколебаний явления Рисса в установке Леманна, состоящей из вертикально расположенной трубы, в нижней части которой расположено устройство охлаждения воздуха и на ее входе присоединен рессивер (рис. 4). При этом, в отличие от классической установки Леманна [2], предполагается, что в рессивер воздух подается нагретым, а на входе в вертикальную трубу воздух локально охлаждается (эффект Босша-Рисса).

3.    Гидравлическая характеристика теплового сопротивления hT(Q) при теплоотводе

В пневмосистеме (рис. 1) вентилятором осуществляется напорное движение нагретого воздуха и между сечениями 1 - 1 и 2 - 2 осуществляется отвод теплоты.

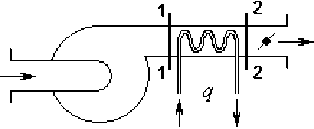
Рис. 1. Схема, пневмосистемы для определения теплового сопротивления при теплоотводе

Запишем уравнение энергии для сечений 1 - 1 и 2 - 2 (рис. 1):

+ W2 + 11 = Р-2 + W2 + . + q + Акт.(1)

Р1    2          Р22

При политропном теплоотводе с показателем политропы п для удельного теплового потока имеем следующее выражение q = с_п (Т 1 — Т 2). Далее, воспользовавшись известными формулами термодинамики идеального газа:

п ^сп = ^С У п

-

-

k

1, Р = рВТ ,

^С р ^C V    R,

111 ^— U 2 = О и ^(Т 1 ^{— Т} 2 ⁾ , — = к, ДЛ ^С У         ¹ 1

( \ п— 1

Р ; 1

а также уравнением неразрывности

Р1™1 = P2W2, из уравнения (1) получается представление

А^

w 2 — W 2

п — к         .

+ с«----г (Т1 — Т2) , п — 1

откуда для потерь давления кт = Аһтрі из-за теплового сопротивления получается выра жение

к (Q, п) = /с_т    к (Т - Т₂) + piQ [1 - ( Т) ”^-11 ,

п — 1             252       \Т2/ J где Q = wi-S - объемный расход нагретого воздуха, S - площадь поперечного сечения проточного тракта (рис. 1). Зависимости теплового сопротивления кт (Q,n) при различных значениях показателя политропы п приведены на рис. 2.

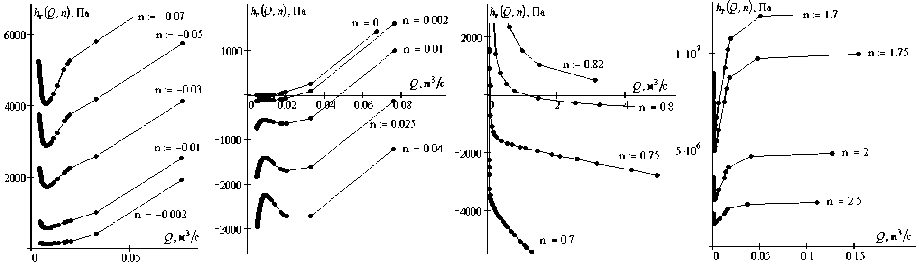
Рис. 2. Характер изменения һ_т (Q/п) при различных показателях политропы п

При изобарном теплоотводе показатель политропы п = 0. Из (1) получается следующее представление для теплового сопротивления изобарного теплоотвода:

A, (Q) = k_TQ 2 , /_V| =

s [1 - ( и )Т

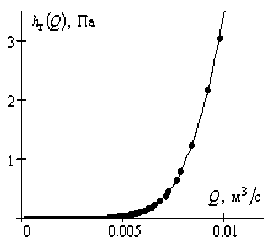
Рис. 3. График зависимости У_т (Q) при изобарном теплоотводе

Зависимость ^_т (Q) при изобарном теплоотводе (Ц > ТД в явлении Рисса представлена на рис. 3. Поскольку /д (Q) с увеличением расхода Q возрастает, то тепловое сопротивление в отличие от феномена Рийке не является механизмом возбуждения автоколебаний в явлении Рисса, когда теплоотвод осуществляется изобарно.

4.    Автоколебания в установке Леманна при теплоотводе

В экспериментальных и теоретических исследованиях термоакустичекие колебания удобно изучать в различных модельных установках, являющихся прототипами соответствующих элементов теплоэнергетического оборудования [2]. Классическая установка Леманна представляет собой трубу Рийке, в нижней части которой расположен рессивер, воздух в который подается нагнетателем [2]. В трубе Рийке автоколебания самовозбуждаются в результате потери устойчивости естественного конвективного течения нагретого воздуха. Отметим, что наличие нагнетателя в установке Леманна не является необходимым ат-трибутом для возбуждения термоакустических автоколебаний. Известно, что в установке Леманна с реверсным движением теплоносителя при достаточной емкости рессивера самовозбуждаются релаксационные автоколебания [10].

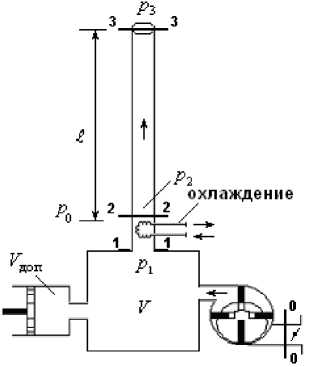
Рис. 4. Схема, установки Леманна, при теплоотводе с ротационным нагнетателем

Составим уравнения движения воздуха в установке Леманна (рис. 4). Согласно принципу Даламбера, уравнение движения воздуха, между сечениями 2 - 2 и 3 - 3 имеет следующий вид:

m2^2 = (р 2 — р з ) S — p 2 glS — F_Tp,

-t где W2 - скорость движения по тока после охлаждения. p2glS - его масса. FTp - сила, вязкостного трения. Полагая hTр = ^|Д- и используя соотношения pi — р2 = hT + һохл, где Нохл - потери давления при обтекании устройства охлаждения, и ро = рз + poglS, где ро - давление в сечении 2-2 снаружи трубы (рис. 4), уравнение (4) окончательно представим в виде

La ^Һ=f (Q2)—р, где La = ^p1    акустическая масса охлажденного столба воздуха, Р = ро

F (Q2) = A (Q2)

-

Н_т р (Q2)

-

-

Р1,

Н_ох л (Q2) — h_T (Q2) ~ напорная характеристика теплоотво-

да вертикальной трубы, A (Q2) = gl (p o — p₂) - давление подъемной силы, Q 2 = Sw₂ - объемный расход воздуха через сечение 2-2 (рис. 4).

Запишем уравнение сохранения массы между сечениями 0 - 0 и 2 - 2:

-т = (poQBх — p2Q2), где dm = Vdpi - изменение массы воздуха в объеме V = IS рессивера в единицу времени, или используя соотношение ^1 = с^, г де ci - скорость распространения звука в объеме нагретого воздуха перед его охлаждением, запишем в форме [5-6]:

dP

Ca    =Q2 . (Р) , где p (Р) = ^Qbx- обращение функции p (Р) представляет потери Р = h^ -, (QBх) при обтекании дросселя в зависимости от входящего расхода приведенного к температуре охлажденного воздуха, Са =    - акустическая гибкость объема V. При включении в работу

Р 2 С 1

ротационного нагнетателя функция p (Р ) заменяется характеристикой нагнетателя.

Таким образом, задача о возбуждении термоакустических автоколебаний явления Рисса в установке Леманна теоретически свелась к определению периодических решений нелинейной автономной системы дифференциальных уравнений (5) - (6). Периодическое автоколебательное решение этой системы определяется предельным циклом на фазовой плоскости соответствующего уравнения интегральных кривых:

C a (F (Q2) — Р ) -Р = L a (Q 2 — p (Р )) -Q 2 ,

геометрические размеры которого определяется величиной волнового сопротивления Z = ^/^ и интенсивностью ^дд²) восходящей (неустойчивой) ветви напорной характеристики F (Q2).

На рис. 5 преведены придельные циклы и соответствующие им формы автоколебаний явления Рисса в установке Леманна при естественном движении воздуха а) и при включении ротационного нагнетателя б).

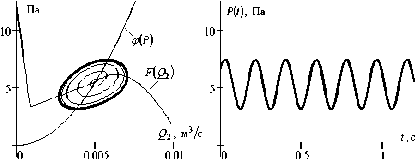
а)

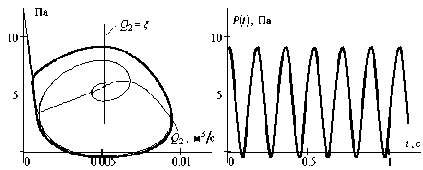
б)

Рис. 5. Автоколебания явления Рисса. в установке (рис. 4)

Рис. 6. Деформация предельного цикла, и форма, релаксационных автоколебаний неизменной амплитуды при увеличении дополнительного объема V,on

С увеличением объема V при помощи присоединенной к нему емкости изменяемого объема 1/цоп (рис. 4) снижается волновое сопротивление Z = л     , ^Р 2 ^С 1 -, и автоколебания

° ус+У.- явления Рисса переходят в релаксационные (рис. 6), амплитуда, которых от дальнейшего уменьшения Z не изменяется, а определяется лишь структурой напорной характеристики теплоотвода F (Q2Y Однако при этом уменьшается частота релаксационных автоколебаний (рис. 6).

5.    Условия самовозбуждения автоколебаний

Самовозбуждение автоколебаний происходит в результате потери устойчивости стационарного течения. Значения объёмного расхода воздуха Q2 и относительного давления Р* на. стационарном режиме определяются из системы (5) - (6), полагая в ней dQ2 dt

= 0, Q 2 —Q *

dp dt

= 0.

P—P *

Для исследования характера, устойчивости стационарного течения воздуха, рассмотрим малые возмущения

Q (t) = Q* + € ^ехР {At} , Р (t) = Р * + d exp {At} (€, d = const) .

Подставляя данные возмущения в исходную динамическую систему (5) - (6), после ее линеаризации приходим к следующему характеристическому уравнению:

A2 + (^Р — F^QpA + -1^ (1 -F ‘ (Q2>' (Р *)) =0, \ Ca       La  /     LaCa где обозначено Р‘ (Q2) = ^Йг\     , ^ (Р*) = SP\

*

^q 2 —^Q2                  ^p— ^P

Согласно критерию Рауса-Гурвица [9], условие устойчивости стационарного течения определяется положительностью коэффициентов полученного характеристического полинома. второго порядка, откуда, следует

C a F‘ (Q*) <  L a ^ (Р *), F' (Q2) ^ (Р *) < 1.

Отметим, что ^yp) >  0 при любых значениях Р >  0. Таким образом, нарушение условий (8) возможно, только когда F ‘ (Q2) > 0.

При выполнении условий самовозбуждения (8) стационарное течение является неустойчивым и в результате даже бесконечно малых возмущений переходит в автоколебательный режим движения. Амплитуда, автоколебаний определяется диаметром предельного цикла, уравнения интегральных кривых (7).

6.    Выводы