Автокомпенсация реактивной мощности в электрических сетях

Цитирование: Павлов, В. Д. Автокомпенсация реактивной мощности в электрических сетях / В. Д. Павлов // Журн. Сиб. федер. ун-та. Техника и технологии, 2021, 14(6). С. 684–688. DOI: 10.17516/1999–494X-0342

Реактивная мощность в сети – нежелательное явление [1, 2]. Ее циркуляция по проводам вызывает тепловые потери в объеме примерно 10 % ее величины. Для ее снижения используют дорогостоящие статические и динамические компенсаторы.

Цель работы – оценка влияния каскада трансформаторов и шунтирующих реакторов на реактивную мощность в сети при симметричной нагрузке.

В настоящей работе применяются электротехнические расчеты.

Самокомпенсация реактивной мощности при симметричной нагрузке

На рис. 1 представлена существенно идеализированная схема подключения вторичных обмоток трансформатора к симметричной индуктивной нагрузке [3]. Сопротивления рассеяния не показаны. Активные составляющие сопротивлений не рассматриваются. Вращающееся магнитное поле создается первичными обмотками (не показаны). Реактивная мощность в сеть не передается (гипотетически).

В части вращающегося магнитного поля и опосредованного взаимодействия его с нагрузкой схема неотличима от рассмотренной в [4], в которой вместо трансформатора использована синхронная явнополюсная машина и в которой источником возбуждения колебаний тока (индуктивного) в любой фазе служат другие (другая) фазы (фаза) нагрузки.

Подобное явление самокомпенсации реактивной мощности известно и в механических системах [5]

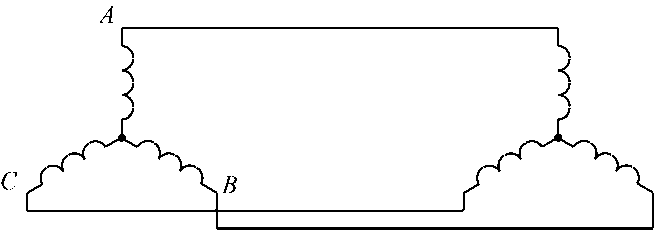
Рис. 1. Самокомпенсация реактивной мощности

Fig. 1. Self-compensation of reactive power

Мгновенные токи, напряжения и мощности (реактивные) фаз, соответственно, равны iA = / sin со/, иA = ItoL cos co/, qA =/2coZsinco/cosco/ =— ZcoZsin2co/

•    7 • С 2л)

l_R = /sin co/--

V з J uR = /coZcos co/--

I 3

1         Г      4л qR = —/"toZsin ZCO/--

2         I       3

L = / sin co/4--

I 3

uc = ItoL cos со/ h-- q, = —/"coZsin 2co/ + —

2 I 3

Здесь L - суммарная индуктивность фазы трансформатора (включая рассеяние) и нагруз- ки.

Сумма мощностей фаз В и С равна

= 2 — /coZsin 2

Чвс ^b^Qc = —/coZsinl 2со/-—I +—/coZsinl 2со/ + —1 = _ 1     . 2со/-4л/3 + 2со/ + 4л/3   2со/-4л/3-2со/-4л/3

2 — /coZsin 2со/ cos--=—/coZsin2co/

Эта величина противоположна мощности фазы А , т. е.

Чв^Чс =-q.v

Это означает, что при оговоренных условиях любая фаза является источником реактивной мощности двух других фаз.

И наоборот, любые две фазы являются источником реактивной мощности третьей фазы.

Таким образом, для данной схемы при симметричной нагрузке происходит самокомпенса-ция реактивной мощности.

Замечание о мощностях фаз

Для того чтобы последняя формула не создавала впечатление, что мощность в любом случае удовлетворяет аналогу первого закона Кирхгофа, ниже приводятся выражения для мгновенных активных мощностей фаз и их соотношение.

Pa

i 7-7 _rl + cos2co/ 1 _₉ _   1 _r

= 1 COL COS" СО/ = Г tot ----------= —/"COZ + —/"COZ COS 2(0/

2       2       2

Рв

1 т 1 т I ~ 4л

= —/"toZ+ —/"toZcOS 2со/--

2        2 I з

1 г2 _ 1 _9 _     (         4л

= — 1 toZ+ —/"toZcOS 2со/Н--

2        2 I       з

1 r2 _    1 _9 _     ( 4Л

Рв + Pc ⁼~^ COL+ —/"COLCOS 2со/--

1 r 1 г2 г             4л

+—/"coZ +—/ coZcos 2со/ н--

2        2 I 3

= I mL I toL— cos2co/-— ftoL— cos2co/ = / coZ / coZcos2co/ 2      2          2      2                 2

Рв + Pc * "Pa

Потоки реактивной мощности в каскаде трансформаторов

Каскад трансформаторов на рис. 2 представлен их упрощенными схемами замещения (без учета рассеяний). Активные сопротивления не рассматриваются.

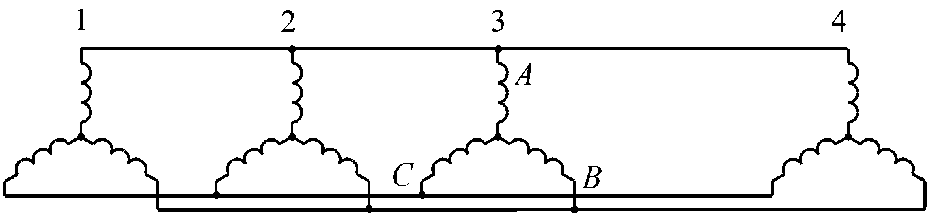
Рис. 2. Каскад трансформаторов

Fig. 2. Transformer cascade

Идеализация этой схемы меньше, чем первой, поскольку реактивная мощность второго и третьего трансформаторов передается в первичную обмотку.

Если трансформаторы идентичны, то поток реактивной мощности от нагрузки делится между ними на равные части. Поэтому поток реактивной мощности на участке 1–2 в три раза меньше, чем на участке 3–4.

В соответствии с этим в реальной сети с ростом числа трансформаторных подстанций и шунтирующих реакторов поток реактивной мощности по мере удаления от нагрузки существенно уменьшается за счет взаимной компенсации реактивной мощности фаз.