Автоматическая система взаимно инвариантного векторного управления переменными технологического состояния аппарата приготовления раствора

Введение. Наряду с совершенствованием технологии автоматизация производства является ключевой составляющей развития любой промышленности: химической, микробиологической, пищевой и др. При автоматизации промышленных производств объектом автоматизации является обычно не отдельный технологический процесс или аппарат, а некий технологический модуль, комплекс или линия со сложными взаимосвязями между его агрегатами, коммуникациями, потоками и пр. Современные системы автоматизации таких комплексов должны обладать широкими функциональными возможностями, новыми техническими характеристиками. Выполнение указанных требований позволяет обеспечить высокую надежность (живучесть) элементов управления, их информативность, функциональность, быстродействие, комфортность работы оператора и пр. [1–3].

Однако все перечисленные качества автоматизированных систем управления технологическими процессами (АСУ ТП) характеризуют не только средства и системы централизованного управления. Корни этих свойств — в так называемых локальных системах автоматического управления (ЛСАУ) [4–6]. Это обусловлено рядом причин. Во-первых, именно ЛСАУ ориентированы на работу с первичной информацией о состоянии технологического процесса. Во-вторых, они непосредственно воздействуют на исполнительные механизмы регулирующих органов управления процессом. Таким образом, именно на нижнем уровне — уровне локальных САУ формируются фундаментальные свойства АСУ ТП. К ним относится, прежде всего, быстродействие управления: очевидно, что никакая системная надстройка не повысит скорость медленно функционирующей системы, непосредственно воздействующей на объект. Постановка задачи. В настоящей статье ставится задача исследовать возможности синтеза САУ локального уровня, обеспечивающие близкое к максимальному быстродействие управления технологическим процессом.

Математическая модель аппарата приготовления раствора (АПР). Аппарат представляет собой технологическую емкость, которая оборудована трубопроводами подачи смешиваемых потоков и отвода смеси, а также эффективной мешалкой. В емкость подаются растворитель с расходом G 0 и раствор некоторого вещества высокой концентрации C 0 с расходом G C , как показано на рис. 1. Управление таким аппаратом сводится к поддержанию заданной выходной концентрации C приготавливаемого раствора и его уровня в аппарате при заданной общей производительности G .

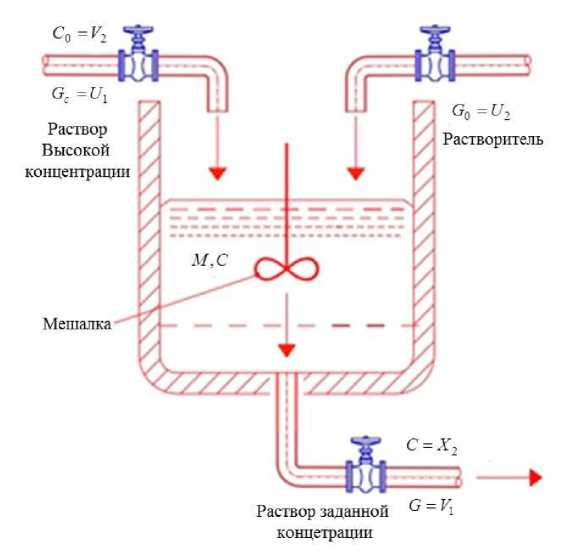
Рис. 1. Расчетная схема аппарата приготовления раствора

Достаточно адекватная математическая модель (ММ) такого аппарата как объекта управления (ОУ) может быть получена на основании закона сохранения количества вещества, применяемого как ко всем компонентам процесса в общем потоке, так и к отдельным его компонентам [7–9].

По закону сохранения количества вещества общее количество раствора в аппарате в условиях нестационарно-сти процесса будет подчиняться следующему уравнению баланса:

d_tM = ( G_o + G _c - G ) • dt ,                                            (1)

где M — количество раствора в аппарате, которое с учетом нестационарности M считается функцией времени; d t — дифференциал переменной по независимому аргументу t — времени.

По этому же закону количество вещества, находящегося в аппарате в растворенном виде, также будет подчиняться составленному для него в отдельности уравнению баланса неустановившегося процесса:

d_t ( C • M ) = ( C_o • G_C - C • G ) • dt ,                                             (2)

где C 0 , C — массовая концентрация.

Концентрация всего раствора в аппарате и концентрация выходного потока обозначаются одинаково — C .

Это обосновано гипотезой об «идеальном смешении» [7], опирающейся на предположение о высокой эффективности мешалки. Преобразуя выражения (1) и (2), получим дифференциальные уравнения (ДУ):

dM = Gc + Go - G , dt dM   dC

C --+ M — = C _o • G_c - C • G .

dt       dt ^{0 C}

Преобразование (4) подстановкой в него (3) позволяет получить корректный вид этого ДУ:

M • dC ⁼ ( C o - C ) • G c - C • G o .

В свете задачи управления технологическим процессом смешения переменными состояния (ПС) объекта следует считать уровень в емкости H = „ и выходную концентрацию C^x2, где символом « = » отмечено «равенство по обозначению». Управляющими воздействиями процесса формирования концентрации на выходе АПР будут GC об и1 и Go об и2. Естественными возмущающими воздействиями для АПР являются технологическая нагрузка на об аппарат — потребляемый технологической линией расход приготовленного раствора ( G = V1) и концентрация исполь- об зуемого сырья (C0 = v2 ).

Таким образом, для получения рабочей ММ аппарата смешения как ОУ необходимо выразить величину H через другие технологические параметры и переменные [7–10]. Это можно сделать через несложную зависимость массы раствора M от его объема V и плотности ρ , которая, в свою очередь, зависит от концентрации C и темпера- туры T :

M = V • Р = H • S • Р (C, T) = kH-1 • H,(6)

где k_H ^{- 1} = S • p ₀, считая в условиях стабилизации концентрации C и температуры T р ( C , T ) = р₀ = const .

Тогда ММ АПР как ОУ в выбранных ПС будет представлена системой ДУ в форме Коши следующего вида:

Х1 = kH • и1 + kH • и2 - kH • v1,(7)

X                      ид • v x2 = -kH • — •(u1 + и2 ) + kH • ——- .(8)

x ₁ x ₁

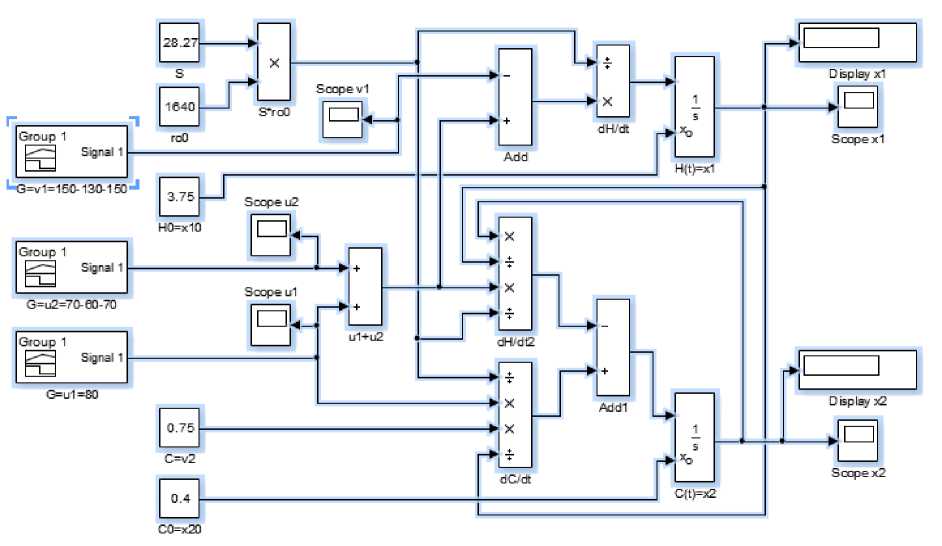
Анализ системы ДУ (7, 8) показывает, что первое ДУ (7) является линейным и определяет для канала управления уровнем свойство астатизма первого порядка. Однако второе ДУ (8) является существенно нелинейным. Поэтому динамические свойства АПР исследованы с использованием схемы имитационного моделирования, приведенной на рис. 2, а. Эта схема послужила также моделью при исследовании динамических свойств системы автоматического управления АПР.

Информатика, вычислительная техника и управление

а)

Signal 1[

(z2-x2)*2

Dis play x1

Gro up 1

Signal

Scope x1

{v2-x2)/v2

*{v2-x2)/v2

Dis play x2

Scope x2

б)

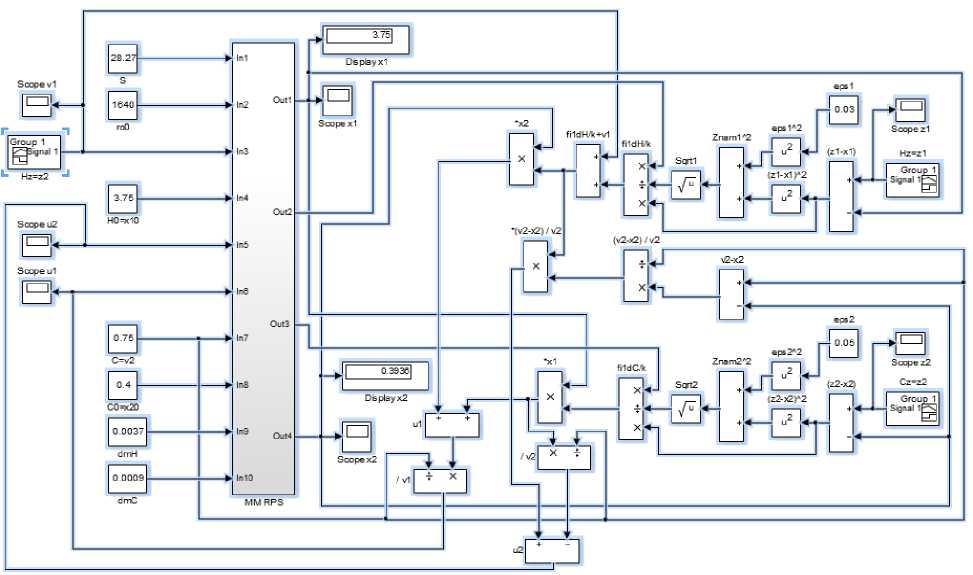
Рис. 2. Схемы имитационного моделирования: АПР как объекта управления (а); САУ АПР (б)

Очевидно, что процедура синтеза законов управления АПР при существенной нелинейности составляющей (8) его ММ неординарна и требует индивидуальных исследований. Это особенно актуально в связи с очевидными ограничениями на величины управляющих потоков G C и G 0 , существующими в реальных технологических схемах при высоких требованиях к точности поддержания концентрации и быстродействию подавления ошибок управления. Последнее обусловлено необходимостью поддержания максимальной производительности АПР в рамках реальных конструктивных и технологических ограничений [5, 8, 11].

Синтез двумерного закона квазиоптимального управления АПР. В предыдущем разделе получена ММ АПР в виде системы ДУ (7) и (8), характеризующейся сложным взаимодействием переменных состояния, управляю-

щих и возмущающих воздействий. Поскольку управлению подлежат две ПС, управление должно быть также двумерным, т.е. векторным. Для синтеза такого управления с учетом сформулированной выше постановки задачи можно воспользоваться подходами, предложенными для различных приложений в работах [5, 8, 11, 12, 13, 14, 15, 16]. Анализ представленных источников позволяет выделить два подхода. Суть первого из них состоит в формировании закона управления объектом на основе желаемой (или эталонной) ММ проектируемой САУ. Суть второго подхода состоит в формировании форсированного закона изменения производных ПС эталонной ММ САУ с гарантированным ограничением по амплитуде. Так, в соответствии с парадигмой этого подхода можно задаться системой желаемых ДУ [15, 16], причем в виде, предложенном в [13, 14]:

• x i = x 2 ;

  
  

x 2 =             a m     2      • [ z ^- ( x i + Ц • x 2 ) ] .

V [ z - ( x , ⁺ И • x 2 ) ] ^{+ 0 2}

Однако такое решение неприменимо к объекту, описываемому ММ (7), (8), т. к. ПС x 1 и x 2 имеют кардинально отличающиеся размерности. Приведение их к единой размерности требует применения размерного коэффициента, величина которого не определена. Кроме того, математическая структура системы (9) не содержит совершенно необходимой в случае управления АПР переменной — задания по уровню z 1 . Поэтому в данном случае неэффективно преобразование базовой ММ 2-го порядка в ММ открытой системы с внешним управлением по аналогии с [14] построением макропеременной, играющей в схеме роль условной комбинированной ошибки регулирования в виде x ^ ( z , x 1 , x ₂ ) = z - ( x 1 + ц₂ • x ₂ ) , где ц 2 — коэффициент согласования ПС.

В связи с этими особенностями ММ ОУ целесообразно отказаться от исходной парадигмы подхода к синтезу квазиоптимального по быстродействию управления для объектов второго порядка, сформулированной в [13, 14]. Анализ уравнений (7–8) показывает, что можно задаться системой желаемых ДУ, распадающихся на два независимых нелинейных уравнения первого порядка вида, предложенного еще в [11, 12]:

^x i =

d m • ( z i - x i )

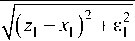
x ₂ =

d m • ( z 2 - x 2 )

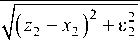
где d mH , d mC — технологические ограничения на скорость изменения уровня и концентрации соответственно; z 1 —

задание по уровню; z ₂ — задание по концентрации; £ 1 и £ 2 — так называемая степень квазиоптимальности управления [12, 13].

Это тем более целесообразно, что обе ПС (и уровень x 1 , и концентрация x 2 ) технологически независимы и быстродействие управления каждой из них желательно с точки зрения максимальной производительности АПР.

Отождествление правых частей уравнений (7) и (10) позволяет получить следующее промежуточное уравнение, связывающее оба технологически обусловленных управления с технологически обусловленной переменной состояния — уровнем x 1 , технологически заданным его значением z 1 и производительностью АПР v 1 :

dmH и + Un —--- kH

•

( z i ^{- x} 1 )

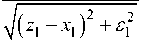
+ Ч.

Аналогично отождествление правых частей уравнений (8) и (11) позволяет получить другое промежуточное уравнение, связывающее оба технологически обусловленных управления с технологически обусловленной переменной состояния — концентрацией x 2 , технологически заданным его значением z 2 и концентрацией сырьевого потока

v ₂ :

U 1 + и ₂

C u i • ^v2    d m

— x ₂ k_H

x i       ( ^z 2 ^{- x} 2 )

-----.              == x      22

( z 2    x 2 i + о 2

Информатика, вычислительная техника и управление

Приравнивая правые части (12) и (13), можно выразить управление u 1 (сырьевой поток) в следующем виде:

Ui =-- v2

dm _Y      ^{( z} i - x )

x 2 '

k^H       ^( z i - ^x i ) 2 + ⁶ 2

. dC „      ⁽ z 2 - x 2 )

+--- X i — I

^^H      ( zz 2 - ^X 2 ) + ⁶ 2

+ V i ■ x 2

Подстановка (14) в (12) позволяет получить выражение для второго управления u 2 (потока растворителя):

и 2 = d m     ⁽ z - ^{x )}    /i - ^x )_ d m x      ^{( z} 2 - ^x 2 )    + V ^f i - ^}                  (i5)

k H  ^ ( Z i - X i ) ² + 6 2 I    ^{V 2} J   k ^{m V 2} ^ ( z 2 - x 2 ) ² + _e 2 I    ^{V 2} J

Выражения (14) и (15) задают векторный закон управления (ЗУ) для АПР по каналам задания уровня и концентрации. Схема имитационного моделирования САУ АПР приведена на рис. 2, б. На этой схеме модель самого АПР представлена блоком (Subsystem) MM RPS.

f u _i )

Существенная нелинейность и структурная громоздкость векторного управления АПР u = I I, сформиро-( u 2 J ванного в соответствии с парадигмой, заданной уравнениями (10–11), оправдывается тремя факторами.

об                                                   об

• i.    Управление обеими переменными состояния (уровнем H = x _i и концентрацией готового раствора С = x ₂) осуществляется обоими управляющими воздействиями (сырьевым потоком раствора высокой концентрации об                                         об

• 2.    Обе переменные технологического состояния x 1 и x 2 регулируются независимо друг от друга, т. е. процесс регулирования уровня не оказывает влияния на процесс стабилизации концентрации, и наоборот.

• 3.    Обе переменные технологического состояния x 1 и x 2 регулируются и стабилизируются независимо от

G_C = u _i и потоком растворителя G 0 = и ₂ ). Таким образом обеспечивается максимальное использование ресурса управления (это важно в связи с существенным ограничением величины потока в реальном трубопроводе с реальным регулирующим органом).

об нагрузки на АПР G = vi, которая представляет собой производительность аппарата, обеспечивающего раствором стабильной концентрации последующие аппараты технологической цепочки.

Эти свойства иллюстрируются рисунками 3, 4 и 5.

На верхнем скриншоте рис. 3 показана последовательная смена задания (Scope z 1) на уровень в АПР. На следующих двух скриншотах проиллюстрированы управляющие воздействия (Scope u 1, u 2), обеспечивающие смену уровня. Видно, что выход на новый уровень обеспечивается параллельным изменением смешиваемых потоков. Поэтому четвертый скриншот (Scope x1) показывает переходный процесс интенсивного изменения уровня, длящийся не более 2 минут, а последний (Scope x2) подтверждает обеспечение неизменности концентрации, т. к. векторный ЗУ f u _i )

и = I I обеспечивает изменение потоков в пропорции, обусловленной заданной концентрацией.

( u 2 J

На рис. 4 верхний скриншот (Scope z 2) показывает последовательную смену задания на концентрацию приготавливаемого раствора. Второй и третий скриншоты (Scope u 1, u 2) иллюстрируют соответствующие изменения управляющих воздействий. Четвертый скриншот (Scope x 1) подтверждает, что уровень при управлении концентрацией остается неизменным (управление обеспечивает одинаковые и противоположные по знаку изменения входных потоков). Последний скриншот (Scope x 2) демонстрирует переходный процесс изменения концентрации, также достаточно интенсивный.

Таким образом, имитационное моделирование процессов управления функционированием АПР по различным каналам подтвердило функциональность и эффективность исходной парадигмы автономного, квазиоптимального по быстродействию и согласованного управления технологическими переменными состояния.

На рис. 5 продемонстрирован эффект от введения в векторный ЗУ переменной v 1 - (Scope v 1). Управляющие воздействия u 1 и u 2 на экранах (Scope u 1) и (Scope u 2) меняются синхронно с нагрузкой v 1 и обеспечивают независимость технологического состояния аппарата от его производительности. Это иллюстрируют осциллограммы на экранах Scope x1 и Scope x2. Полученные в ходе аналитических исследований и преобразований, а также в ходе имитационного моделирования автоматической системы взаимно инвариантного векторного управления технологическим состоянием аппарата приготовления раствора результаты позволили сделать изложенные ниже выводы.

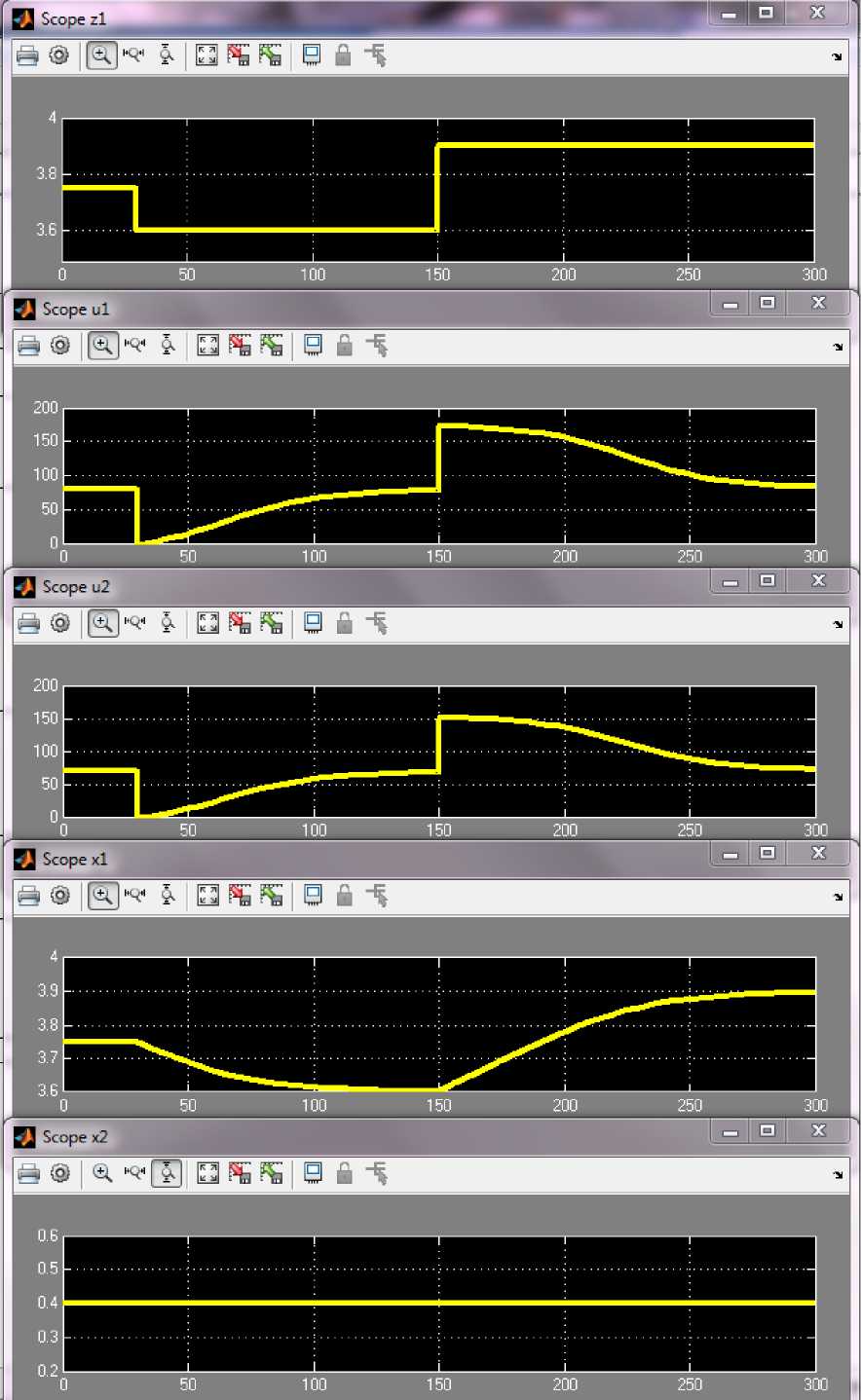
Рис. 3. Переходные процессы изменения уровня в АПР

Информатика, вычислительная техника и управление

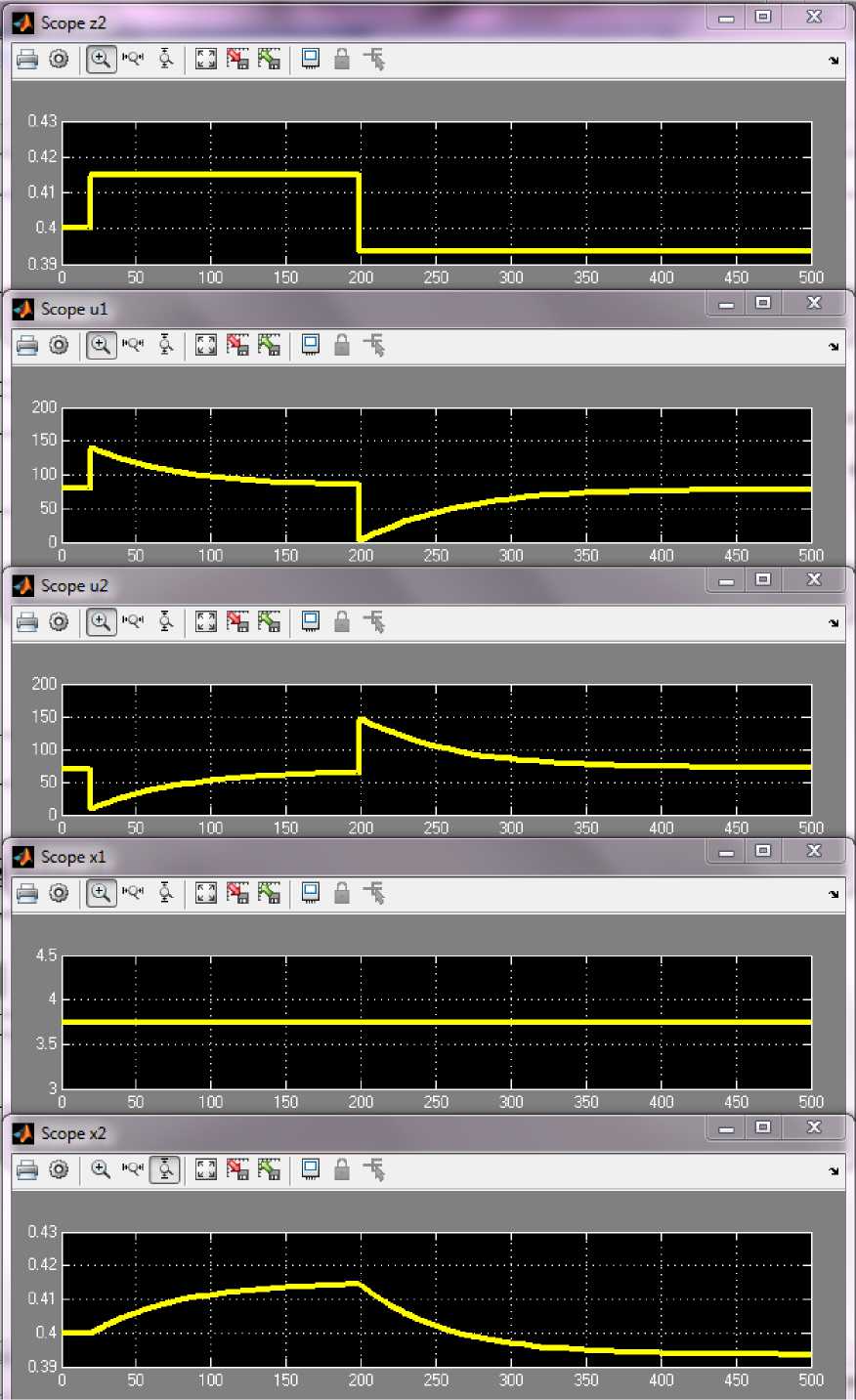
Рис. 4. Переходные процессы изменения концентрации в АПР

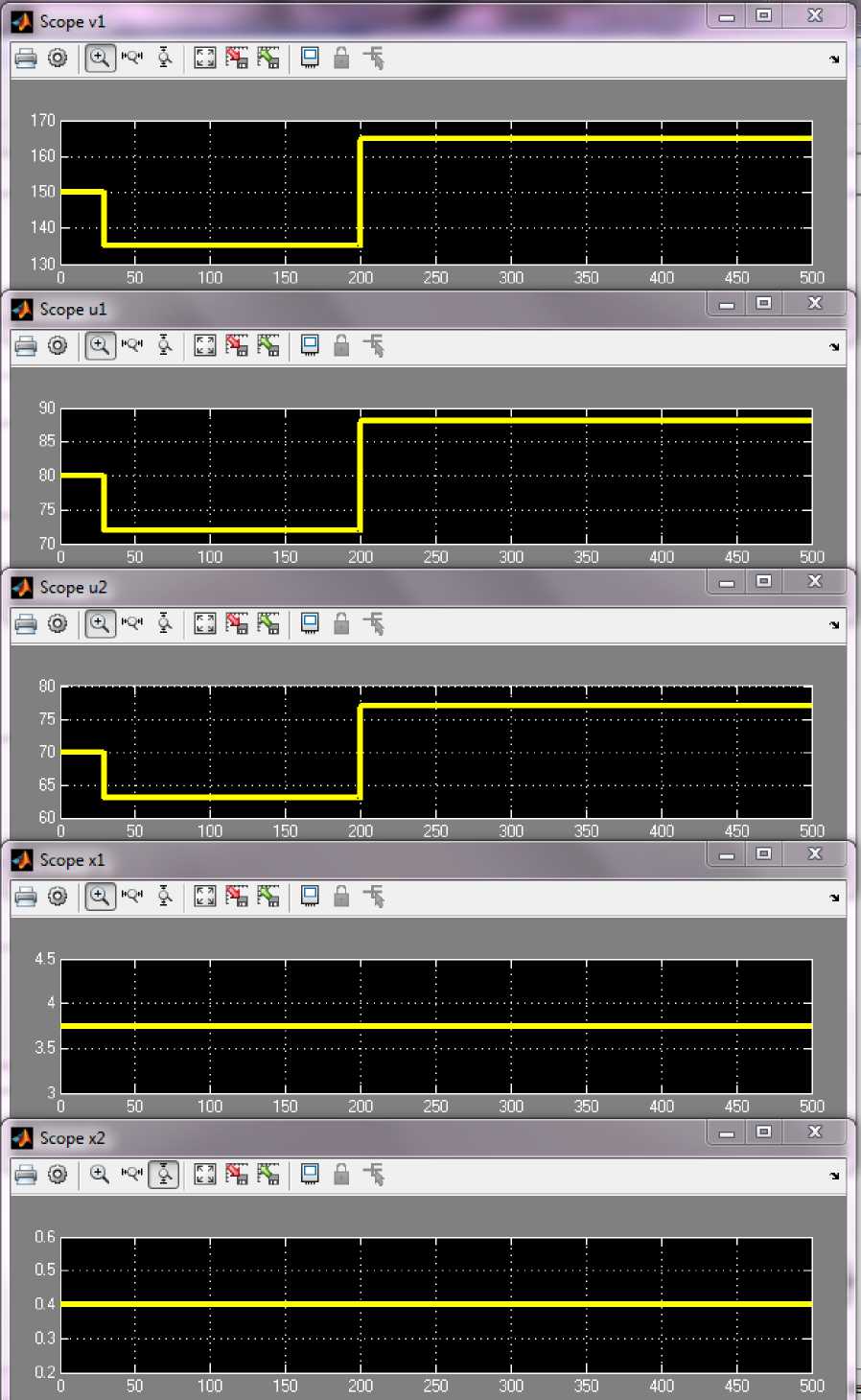
Рис. 5. Переходные процессы при изменении производительности АПР

Информатика, вычислительная техника и управление

Выводы.

• 1.    Полученный в ходе проведенной работы векторный двухвходовый закон управления показал высокую эффективность решения задачи управления основными переменными технологического состояния аппарата приготовления раствора. Удалось достичь следующих результатов:

• —    более полное, по сравнению с одноконтурными системами регулирования, использование ресурса управления за счет одновременного и согласованного воздействия на управляемую переменную по каналам всех влияющих входов;

• —    обеспечение независимости контуров управления переменными технологического состояния аппарата приготовления раствора — как друг от друга, так и от внешних возмущений.

• 2.    Сочетание идеологии синтеза законов управления на основе желаемых или эталонных математических моделей проектируемых систем с идеологией квазиоптимизации быстродействия управления можно считать перспективным подходом к задачам построения систем векторного управления многосвязными нелинейными объектами для обеспечения взаимной независимости и высокой интенсивности управления их переменными состояния.