Автоматический способ оценки состояния геомагнитного поля

Работа направлена на создание теоретических и программных средств анализа параметров геомагнитного поля и выделения возмущений в период повышенной активности Солнца. Известно, что изучение вариаций магнитного поля Земли является основой оценки свойств и состояния электромагнитных полей в околоземном космическом пространстве [1]. В результате воздействия солнечной активности на околоземное космическое пространство происходят магнитосферные возмущения различного масштаба и длительности, которые негативно воздействуют на современные технологические системы [1, 2]. В магнитном поле также могут проявляться катастрофические природные события или процессы на стадии их подготовки [2].

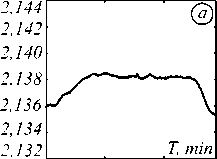
Наблюдения за магнитным полем осуществляются более чем в 70 странах. Для этого традиционно используются наземные магнитометры. Особенно важны наблюдения в высокоширотных областях, а прогноз космической погоды необходим для надёжной работы технической инфраструктуры Арктического региона. Регистрируемые вариации геомагнитного поля имеют сложную нестационарную структуру. На рис. 1 в качестве примера показаны горизонтальные компоненты геомагнитного поля в спокойный период и во время магнитной бури. В ночное время геомагнитная активность возрастает, а во время магнитных бурь могут наблюдаться резкие выбросы и колебания [1, 3, 4]. Помимо суточного хода, геомагнитные данные имеют сезонный, вековой ход и подвержены влиянию 11-летнего цикла солнечной активности [1].

Сложная структура вариаций геомагнитного поля существенно усложняет процесс их изучения и делает малоэффективными для решения поставленной задачи классические методы анализа данных [1, 4–6], которые не позволяют выявлять некоторые закономерности и приводят к потере важной информации. Не- достатком используемых классических методов и подходов также является недостаточная степень их автоматизации, что весьма важно в задачах оперативной обработки данных околоземного пространства и прогноза космической погоды.

Н^<104. пТ

О 500 1000

2,144 2.142

2,140

2,138

2,136 2,134 2,132

Т, min

0    500 1000

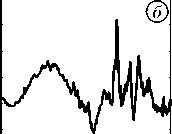
Рис. 1. H-компоненты магнитного поля Земли:

• а)    спокойная суточная вариация;

• б)    возмущённая суточная вариация

Как показывают последние исследования [4, 7– 17], естественным и наиболее эффективным способом описания таких данных являются нелинейные адаптивные аппроксимирующие схемы. Основанные на этом подходе методы декомпозиции на эмпирические моды (ДЭМ) [16, 17] и адаптивные вейвлет-разложе-ния [4, 8–15] получают в настоящее время интенсивное развитие в обработке и анализе сложных структур данных [4, 8–15]. Оба этих метода учитывают особенности структуры сигнала и позволяют описывать процессы со сложной структурой [18, 19]. Достоинством вейвлет-анализа является большое число ортогональных базисов с компактными носителями и наличие быстрых вычислительных алгоритмов [19]. Основной сложностью при его использовании является неочевидность выбора базиса для решения конкретной задачи [19–21]. В то же время для задач аппроксимации функции предложены критерии выбора вейвлет-базиса и построены вычислительные алгоритмы, позволяющие адаптивно подобрать базис и минимизировать погрешность получаемой аппрокси- мации [19, 21]. В отличие от вейвлет-преобразования в методе ДЭМ функции базиса определяются непосредственно из данных и построенный базис апосте-риорен [20, 22]. Поэтому в большинстве случаев извлекаемые аппроксимирующие компоненты могут эффективно применяться только для обработки того сигнала, из которого они были извлечены. Такой базис является эмпирическим и для аппроксимации вариаций геомагнитного поля с непрерывно изменяющейся структурой не является достаточно эффективным. Недостатком ДЭМ также является не полностью разработанная теоретическая база [18, 20]. В частности, линейная независимость аппроксимирующих компонентов не доказана математически, и свойство ортогональности выделенных эмпирических мод может быть проверено только апостериорно [23]. В свою очередь, вейвлет-анализ имеет хорошо разработанный математический аппарат и получает широкое распространение в области геофизики. На основе вейвлет-преобразования предложены способы анализа особенностей, возникающих в геомагнитном поле в периоды мощных солнечных вспышек [24, 25], разработаны алгоритмы автоматического определения периодов начальной фазы бури [26], созданы алгоритмы удаления шума и исключения периодической компоненты, вызванной вращением Земли [27, 28]. В данной работе вейвлет-анализ применялся совместно с нейронными сетями. Аппарат нейронных сетей широко применяется в задачах распознавания образов и анализа данных [29-31]. Нейронные сети также показали свою эффективность и в области геофизики [14, 32, 33]. Этот аппарат позволяет воспроизводить сложные нелинейные зависимости данных [32-34], выявлять скрытые закономерности в данных и легко реализуем в автоматическом режиме [35, 36].

В основе разработанного авторами способа лежат кратномасштабное вейвлет-разложение (КМА) [19] и радиальные нейронные сети [36]. На основе КМА в работе выполняется декомпозиция вариаций геомагнитного поля на разномасштабные компоненты, ха-растеризующие возмущённость поля, и подавляется шум. Выделенные компоненты поступают в радиальные нейронные сети, выполняющие оценку степени их возмущённости. Детальное изучение структуры геомагнитных данных (на примере горизонтальной компоненты магнитного поля Земли (Н-компоненты)), выполненное на основе КМА, позволило выделить признаки возмущённости поля и на их основе сформировать образы классов для радиальных слоёв нейронных сетей. Это повысило качество решения задачи на основе нейронных сетей и, в отличие от традиционной архитектуры, позволило существенно уменьшить количество используемых примеров в их радиальном слое.

Для решения задачи в данной работе сформированы шесть радиальных нейронных сетей, объединённых в коллектив электронных экспертов. Формирование заключения о состоянии геомагнитного поля вы- полняется на основе решающего правила, использующего комбинации решений экспертов коллектива.

Для апробации способа использовались геомагнитные данные станции «Паратунка» (с. Паратунка, Камчатский край, регистрацию выполняет ИКИР ДВО РАН) за период 2002-2008 гг. Выполненный анализ данных в периоды повышенной геомагнитной активности показал перспективность применения разработанного способа и возможность его использования в задачах прогноза космической погоды и предсказания сильных магнитных бурь.

Описание способа

Декомпозиция вариаций геомагнитного поля на разномасштабные компоненты

В качестве базового пространства регистрируемых дискретных данных f₀ ( t ) рассматривается замкнутое пространство с разрешением j = 0:

V = clos, _2f12 ⁰ ф (2 ⁰ t - k )): k g Z ), L ⁽ R )

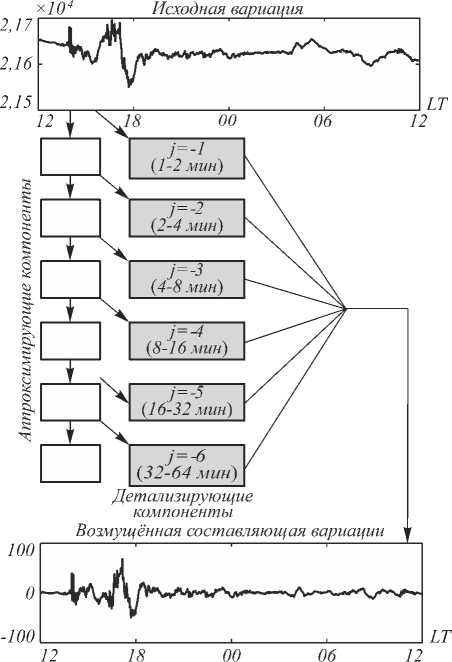
порождённое скэйлинг-функцией фG L ² ( R ) [19]. На основе кратномасштабного вейвлет-разложения до уровня m можно получить представление данных в виде суммы аппроксимирующей и детализирующих компонент:

f , ( t ) = J 1 g [ 2 j t ] + f [ 2 ^- m t ] ,                     (1)

где g [2jt ] g Wj, Wj - пространство с разрешением j, порождённое вейвлет-базисом Тjn (t) = 2j/2 T(2j t - n), разномасштабные детализирующие компоненты g [2j t] = I djnnTj n(t), dj n = (f, T j,n), j - масштаб; ап-n проксимирующая компонента

f [2-mt 1 = c .ф .(t), c ,=( f ,ф .V

L ] k -m , k 1 - m , k     , - m , k       , ^ф- m , k /

В данной работе использовались вейвлеты Т j _n ( t )

и скэйлинг-функция ф m , _k ( t ) Добеши порядка 3.

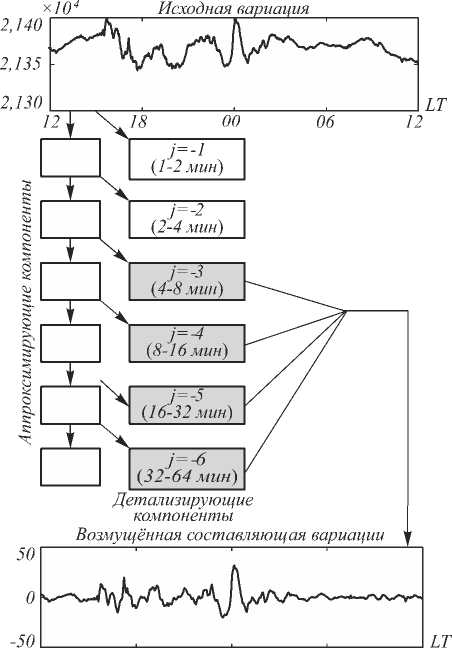
Схема представления данных на основе отображения (1) показана на рис. 2.

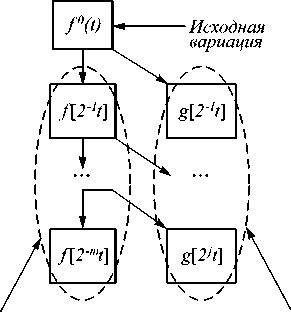
Аппроксимируюгцие компоненты'

Детатзнрующие компоненты

Рис. 2. Схема разложения данных до уровня m

Введение классов состояний геомагнитного поля и определение их признаков

Характеристикой состояния геомагнитного поля является индекс геомагнитной активности K [1]. В работе рассматривались три возможных состояния геомагнитного поля, и было принято:

• 1)    «спокойное» состояние ( 1-й класс ), если суммарный за сутки индекс геомагнитной активности Z к <  10;

• 2)    «слабовозмущённое» состояние ( 2-й класс ), если 10 <  Z к <  18;

• 3)    «возмущённое» состояние ( 3-й класс ), если Z K >  18.

Детальное изучение структуры геомагнитных данных показало [4, 14, 15, 37, 38], что коэффициенты d j_,n детализирующих компонент g [ 2^jt ] масштабов j = -1, -2,…, -6 характеризуют возмущённость поля и в периоды повышения геомагнитной активности существенно возрастают их абсолютные значения. На рис. 3 в качестве примера, показаны детализирующие компоненты вариаций геомагнитного поля масштаба j = -4 в периоды «спокойного» и «возмущённого» состояний поля. Следуя данным результатам, абсолютные значения коэффициентов компонент d_{j , n} примем за меру их геомагнитной возмущённости . За меру геомагнитной возмущённости компоненты g [ 2^jt ] примем максимум абсолютных значений её коэффициентов: V = max d .

g_{j           n}         j , n

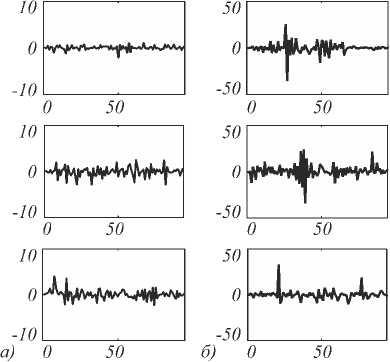
Рис. 3. Детализирующие компоненты вариаций геомагнитного поля масштаба j = -4, полученные с помощью вейвлета Добеши 3-го порядка: а) периоды «спокойного» состояния поля, б) периоды «возмущённого» состояния поля

В соответствии с рассматриваемыми состояниями поля будем считать, что компонента g [ 2^jt ] может иметь одно из трёх возможных состояний – «спокойное», «слабовозмущённое» или «возмущённое». Выше показано, что состояние компонент g [ 2^jt ], j = -1, -2,…, -6 определяет состояние геомагнитного поля. Для оценки его состояния введём следующее решающее правило :

• 1)    если все компоненты имеют «спокойное» состояние либо только одна из компонент имеет «слабовозмущённое» состояние, то геомагнитное поле имеет «спокойное» состояние (1-й класс);

• 2)    если хотя бы одна из компонент имеет «возмущённое» состояние, то геомагнитное поле имеет «возмущённое» состояние (3-й класс);

• 3)    в остальных случаях считается, что поле имеет «слабовозмущённое» состояние (2-й класс).

Оценку состояния каждой из 6 выделенных компонент будем выполнять на основе радиальных нейронных сетей, способ формирования которых описан ниже.

Формирование радиального слоя нейронной сети

Радиальные нейронные сети традиционно имеют три слоя [36]: входной слой; скрытый слой примеров (радиальный слой), содержащий признаки классов; выходной линейный слой, определяющий принадлежность входного образа к классу.

В радиальном слое выполняется следующее преобразование входных данных [36]:

• 1.    Оценка состояния нейронов на основе функции взвешивания r = | p -- w^b , где p - вектор входа, w – вектор примера, b – смещение.

• 2.    Используя пороговую функцию активации, оценка меры близости входного вектора и примера.

Когда расстояние r между вектором примера w и входным вектором p уменьшается, выход функции активации приближается к значению «1», в противном случае — к значению «0».

В соответствии с постановкой задачи входным вектором нейронной сети является компонента g[2jt]. Задачей нейронной сети является определение её состояния. Мерой геомагнитной возмущённости компоненты g[2jt] является введённая выше величина Vg = max dj,n|. Представленные на рис. 4 значения величин V и V , определённые для компонент в g-2          g-6

периоды «спокойного», «слабовозмущённого» и «возмущённого» состояний поля, показывают, что диапазоны их значений имеют существенное наложение. Это обусловлено сложным характером процесса и отсутствием чётких границ между рассматриваемыми классами. Учитывая данные особенности процесса, введём следующие подклассы состояний компонент :

• 1)    для «спокойного» состояния - подкласс « а -спокойных» ( K 1 ):max | d jn | <  T j и « в - спокойных» ( к₂ ): j <  max| d j„ | <  T»' ;

• 2)    для «слабовозмущённого» состояния - подкласс « а -слабовозмущённых» ( к ₃): T j ¹<  max| d j , n | <  T j ² и « в -слабовозмущённых» ( к₄ ): T j ² <  max| d j , n | <  T j ²;

• 3)    для «возмущённого» состояния - подкласс « а - возмущённых » ( к₅ ): T j ²<  max| d j , n | <  T j“³ и « в - возмущённых »( к₆ ): max| d j , n | >  T^¹ .

При обучении нейронной сети пороги T j¹ , Tj ¹ , T j¹ , Tj², Tp , определяющие принадлежность входного признака подклассу, могут быть оценены путём минимизации ошибки сети на множестве обучающих векторов.

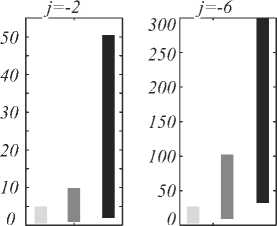
"Спокойное ” состояние

■ "Слабовозмущённое " состояние

■ "Возмущённое ’’состояние

Рис. 4. Значения величин V и V , определённые для

S - 2         S - 6

компонент в периоды «спокойного», «слабовозмущённого» и «возмущённого» состояний поля (в оценках использовалось 100 «спокойных» вариаций поля,

190 «слабовозмущённых» вариаций поля и 86 «возмущённых» вариаций поля)

Введённые выше меры геомагнитной возмущён-ности определяют признаки рассматриваемых подклассов. Используя меру возмущённости коэффициента – его абсолютное значение d_{j , n} , для каждого введённого подкласса к i в радиальном слое нейронной сети создадим один пример P_{j K} i по правилу :

J

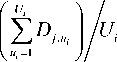
– номер компо-

нитного поля основано на решениях нейронных сетей коллектива и выполняется с помощью введённого выше решающего правила.

О

Примеры: --------;---х

—□- <.<а-спокойный»

—■- «^-спокойный»

—А- «а-слабо«озму-щённый»'

—▲- <ф-слабовозму-щённый»'

-О- «а-возмущённыи» ^^^^^з^-возмущённыиу^

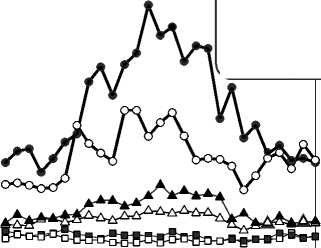
12       18       00      06      12

Рис. 5. Примеры подклассов радиального слоя нейронной сети для масштаба j = -6

LT

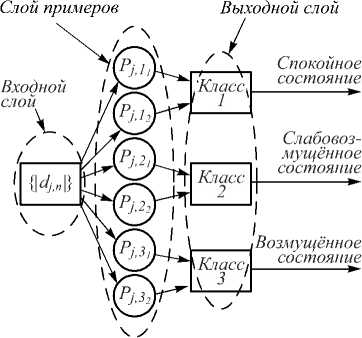
Рис. 6. Архитектура нейронной сети

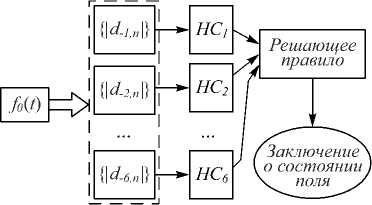
Рис. 7. Структура коллектива нейронных сетей

Оценка эффективности способа

С помощью построенного коллектива нейронных сетей выполнена оценка состояния вариаций геомагнитного поля, полученных на станции «Паратунка» (Камчатский край) за период 2002–2008 гг. Результаты работы коллектива представлены в табл. 1. Для оценки эффективности предлагаемого способа выполнено сравнение полученных результатов с результатами работы традиционной радиальной нейронной сети, на вход которой подавались исходные вариации геомагнитного поля (без применения вейвлет-преобразования). Примеры-образы радиального слоя такой сети, в соответствии с процедурой (2), создавались следующим образом:

p =

Результаты работы традиционной нейронной сети, представленные в табл. 1 (правый столбец), подтверждают эффективность предлагаемого способа и возможность его использования для автоматического определения степени возмущённости регистрируемых вариаций геомагнитного поля.

Табл. 1. Погрешность работы нейронных сетей

Анализируемый период	Погрешность коллектива сетей, %	Погрешность традиционной сети, %
2002 г.	18,58	48,82
2003 г.	11,96	71,4
2004 г.	19,89	51,16
2005 г.	18,39	54,52
2006 г.	18,57	55,7
2007 г.	23,01	60
2008 г.	18,85	54,37

Анализ работы разработанного коллектива нейронных сетей в периоды повышенной геомагнитной активности показал, что более чем в 70 % случаев накануне сильных и умеренных магнитных бурь фиксируются слабые возмущения геомагнитного поля (было проанализировано 97 событий). На рис. 8, 9 в качестве примера показаны результаты работы коллектива в периоды двух событий – магнитной бури с резким началом 02 октября 2013 г. и магнитной бури с постепенным началом 20 апреля 2005 г. За двое суток до момента начала первой магнитной бури, 29 сентября, на Солнце произошла протонная вспышка класса С1.2 продолжительностью 200 мин., максимум которой наблюдался в 23:39 UT. Скорость солнечного ветра 1 октября плавно выросла c 250 до 400 км/с, в высоких широтах было зарегистрировано постепенное начало бури в 07.48 UT [39]. В верхней части рис. 8 показаны значения индексов геомагнитной активности K (K-индексы), ниже изображены вариации геомагнитного поля (H-компоненты). В нижней части рис. 8 показаны результаты оценки состояния вариаций геомагнитного поля с помощью построенного коллектива. Видно, что накануне магнитной бури, 1 октября, коллективом нейронных сетей зафиксированы слабые возмущения. На анализируемых средних широтах внезапное начало магнитной бури было зарегистрировано 2 октября примерно в 01:52 UT [39].

Постепенное начало второй анализируемой магнитной бури было зарегистрировано на средних широтах 20 апреля примерно в 03:00 UT. Скорость солнечного ветра с начала суток возросла с 380 до 540 м/с. Как показывает анализ рис. 9, за двое суток до события коллективом нейронных сетей зафиксированы слабые возмущения геомагнитного поля.

Полученные результаты согласуются с результатами работ [13, 14] и важны для прогноза состояния околоземного космического пространства и предсказания сильных магнитных бурь.

К-индекс: 21100000 01212122 56432333 20000211 10000000

НхЮ4, пТ

_________________________________________________I__________________________________________________I__________________________________________________I__________________________________________________I_________________________________________________ 30.09.13 01.10.13 02.10.13 03.10.13 04.10.13

Спокойное

Слабовозмущённое

Возмущённое

Спокойное

Спокойное

Рис. 8. Результаты оценки состояния вариаций геомагнитного поля за период 30.09.2013–04.10.2013

К-индекс: 32212012 33313211 21222222 25344222 01110101 НхЮ4. пТ 2,140 2,135 2,130

17.04.05 18.04.05 19.04.05 20.04.05 21.04.05

Спокойное

Слабовозмущённое

Слабовозмущённое

Возмущённое

Спокойное

Рис. 9. Результаты оценки состояния вариаций геомагнитного поля за период 17.04.2005–21.04.2005 гг.

Детальный анализ спектрально-временных характеристик вариаций поля в периоды магнитных бурь показал, что в большинстве случаев геомагнитные возмущения попадают в различные детализирующие компоненты. На рис. 10, 12 показаны деревья вейв-лет-разложения вариаций геомагнитного поля для рассматриваемых магнитных бурь, серым цветом отмечены компоненты, которые были определены нейронными сетями как «возмущённые». Видно, что в первом случае геомагнитные возмущения зафиксированы во всех компонентах, что говорит о сложном спектре вариаций и многомасштабном характере процесса. Во втором случае отклонения зафиксированы в детализирующих компонентах 3 – 6-го масштабов. Также на рис. 10, 12 показаны исходные вариации геомагнитного поля и их возмущённые составляющие, полученные путём восстановления «возмущённых» детализирующих компонент. Построенные вейвлет-спектры возмущённых составляющих вариаций поля, показанные на рис. 11 и 13, подтверждают сложный многомасштабный характер анализируемых процессов.

Заключение

В работе описан автоматический способ оценки состояния геомагнитного поля, основанный на совмещении вейвлет-преобразования с радиальными нейронными сетями. Анализ работы построенного коллектива нейронных сетей подтвердил эффективность предлагаемого способа. Исследование спектрально-временных характеристик магнитных бурь (проанализировано 86 событий) показало, что возникающие в геомагнитном поле возмущения в своём большинстве имеют сложную спектральную структуру и проявляются в различных компонентах вариаций поля. Замечено, что накануне бурь предлагаемым способом фиксируются слабые возмущения геомагнитного поля, что важно для прогноза состояния око-

Камчатский край (регистрацию данных выполняет ИКИР ДВО РАН).

лоземного космического пространства и предсказания сильных магнитных бурь.

В экспериментах использовались вариации геомагнитного поля, полученные на станции «Паратунка»,

Рис. 10. Вариации геомагнитного поля в период магнитной бури 02 октября 2013 г. и её возмущённая составляющая

12        18         00         06        12

Рис. 12. Вариации геомагнитного поля в период магнитной

12     18      00      06     12

Рис. 11. Вейвлет-спектр возмущённой составляющей вариации геомагнитного поля в период магнитной бури 02 октября 2013 г.

Рис. 13. Вейвлет-спектр возмущённой составляющей вариации геомагнитного поля в период магнитной бури 20 апреля 2005 г.

Работа выполнена при финансовой поддержке Российского научного фонда, проект № 14-11-00194, а также Фонда содействия развитию малых форм предприятий в научно-технической сфере (программа «УМНИК») договор № 4024ГУ1/2014 и частичной поддержке Министерства образования и науки Российской федерации в рамках договора № 02.G25.31.0058 от 12.02.2013.