Автоматизация инженерных расчётов

Эмуляция – «Emulation», имитация функционирования одного устройства посредством другого устройства или устройств вычислительной машины, при которой имитирующее устройство воспринимает те же данные, выполняет ту же программу и достигает того же

Справочник позволяет в автоматизированном режиме:

• -    строить эпюры продольных сил N(z) и перемещений W(z);

• -    рассматривать стержни постоянного, ступенчатого, переменного, в том числе заданного графически сечения;

• -    загружать стержни как постоянными и переменными, распределенными по заданному закону нагрузками;

• -    рассматривать стержни с упругими опорами и решать задачи растяжения-сжатия стержней в упругой среде;

• -    выполнять проверочные и проектные расчеты, подбирать сечения по условиям прочности или жесткости.

Размещение эмулятора в книге Exel

Для создания эмулятора используем язык программирования Visual Basic for Application (VBA), так как в Excel уже встроена специальный редактор для создания программ в Excel.

• 1.    Запускаем Excel.

• 2.    Выполняем блиц-команду (зажимаем две клавиши) «Alt» и «F11».

  

  Рисунок 1. Окно создания документа «Наш шаблон»

  
  
  

  Рисунок.2. Этап создания шаблона

  
  

• 3.    Создаём шаблон и сохраняем его.

• 4.    После чего записываем три строчки, при этом строчка, которая начинается с апострофа, является комментарием. Слово «Sub» указывает на начало программы, «program ()» - название программы, которое можно изменить, например на «Макрос ()».

Шаблон представляет собой лист книги Excel.

Рисунок.3. Панель инструментов

Формулы прописываются с помощью языка программирования Visual Basic, или встроенных функций электронных таблиц Exel.

Шаблон состоит из полей «Исходные данные», «Расчётная схема» и «Таблица расчётов».

Также в шаблоне имеются поля построении диаграмм продольных сил, продольных перемещений, диаграммы площади поперченного сечения и нормальных напряжений.

В поле «Исходные данные» размещены размеры бруса (L), длина участков – а, сечения участков–А1, А2 …Аi, активные продольные силы – Р, распределенная нагрузка q, модуль упругости Е.

Постановка задачи и ввод исходных данных

Зададим условия исследования «Растяжение-сжатие стержня ступенчатого сечения сосредоточенной силой и переменной по линейному закону распределенной нагрузкой с кинематическим граничным условием».

Дано: двухсоставной стальной стержень, имеющий геометрические координаты L=500 мм и а=200 мм; площади поперечного сечения А1 =250 мм2, и А2=200 мм2; модуль упругости Е; продольная сила Р1=8000 Н.

Необходимо определить силу Р2, которая вызовет перемещения стержня W(l) на ∆ =0,1 мм.

Для решения задач с использованием предлагаемого эмулятора необходимо составить расчётную схему, выполнить её можно в любом графическом редакторе (в данной работе расчётная схема или математическая модель) выполнена в программе Sketch up – построения исследовательские.

Таблица 1

Наименование	Обозначение	Ед. изм.
Длина стержня	L	мм
Сосредоточенная сила	P	Н, кН
Распределенная нагрузка, изменяющаяся в общем случае по определенному закону	q(z)	Н/мм
Текущая координата поперечного сечения	z	мм
Нормальная (продольная сила) в поперечном сечении z, (равнодействующая поперечных сил в сечении сил в сечении): N(z) =σ(z)×А(z); N, σ> 0 - стержень растянут, N, σ <0 - стержень сжат.	Nz	Н, кН
Площадь поперечного сечения	Az	2 мм
Нормальное напряжение в точках поперечного сечения, при растяжении–сжатии σ(z)=N(z)/А(z).	σ(z),	Н/мм2 МПа
Продольное  перемещение  поперечного  сечения  с координатой z;	W(z)	мм
Относительное удлинение (линейная деформация) точек поперечного сечения z;	εz(z)
Модуль упругости материала стержня	Е	МПа
Расчетное  сопротивление,  допускаемые  нормальные напряжения материала стержня	Ry, [σр], [σсж],	Н/мм2
Допускаемое продольное перемещение.	W	2 мм

Таблица 2

Наименование	Обозначение	Ед. изм.
Уравнение равновесия элемента стержня, выделенного двумя сечениями на бесконечно малом расстоянии dz	dN = ± q × dz ± P	мм
Геометрическое соотношение (формула Коши)	ε(z) = dW / dz
Физическое соотношение (закон Гука):	ε(z) = σ(z) / E;
Зависимость между продольными силами и перемещениями
В дифференциальном виде	N' = – q, W' = N/EA	Н

	dN = - q(z)xdz - P, dW/dz = N(z) / EA(z)		Н
W[z(i+1)] = W[z(i)] + N[z(i)]xAL / (ExA[z(i)]),
Шаг разбиения длины стержня при численном интегрировании	AL		мм
Граничные условия, промежуточные упругие опоры, упругая среда
Свободный конец	N(z=0) = 0 N(z=L) = 0		Н
Жестко закрепленный конец	W(z=0) = 0 W(z=L) = 0		Н
Упруго закрепленный конец	N(z=0) = W(z=0) /δ = W(z=0) ×c; N(z=L) = - W(z=L) /5 = - W(z=L)xc
Упругая промежуточная опора в сечении, z = d	N(d+AL) = N(d) + W(d)/5 = N(d) + W(d)xc
Упругая промежуточная опора в сечении z = d может моделироваться внешней нагрузкой	P(d)=-W(d)xc
Податливость опоры	5	мм/Н
Жесткость опоры	1/5	н/мм
Упругая среда может моделироваться наличием внешней распределенной нагрузки	q(z) = -W(z)xe
Заданная податливость среды	в	(Н/мм)/мм
Расчет на прочность и жесткость
Проверочный расчет: при заданных нагрузках, размерах и материале стержня проверить
Условия прочности	o(z)max < [o] (Ry),	Н/мм2
Условия жесткости	Wmax < [W].	Н

Моделирование исследовательского решения

Задачу предлагается решить в два этапа

Ввести исходные данные указанные в условии.

B12        ’ ; | X ✓ Z =(B11 B10)/((B4 B5}/B16)

А В C D_______E_______F

1 Раздел 1.1 РАСТЯЖЕНИЕ-СЖАТИЕ СТЕРЖНЕЙ С ПРЯМОЙ С

Растяжение-сжатие стержня ступенчатого сечения сосредоточенной с распределенной наг| Исходные данные чным условием Расчетная схеш

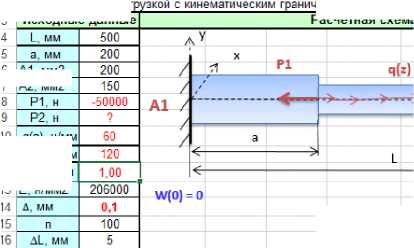
Рисунок 5. Ввод исходных данных

6 |А1, мм2

7 IA2. мм2

10 qi'a'l, н/мм

11 | q(L), н/мм I2 1 Ад, н/мм 13 1е. н/мм2

О 1_ 0 X 7 Ф Q. Ф С О Е

Л ЕС га ? О R С

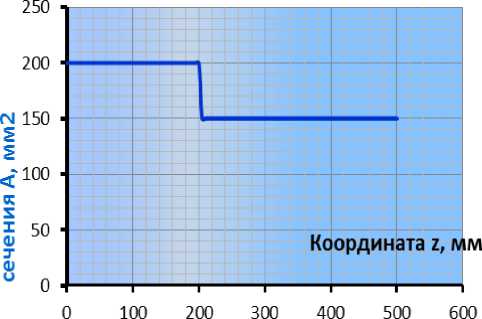
Рисунок.6. Диаграмма поперечного сечения

На первом этапе вводим допущение, что продольная нагрузка Р2 и найдем реальное перемещение бруса

Формирование решения с помощью справочника:

• -    продольное перемещение в начале жестко закрепленного бруса W(0)=0 (рис. 5), подтверждаем в ячейке G22, рис. 7;

• -    реакция в опоре не известна, поэтому ячейка Nz – лоббируемая (F22);

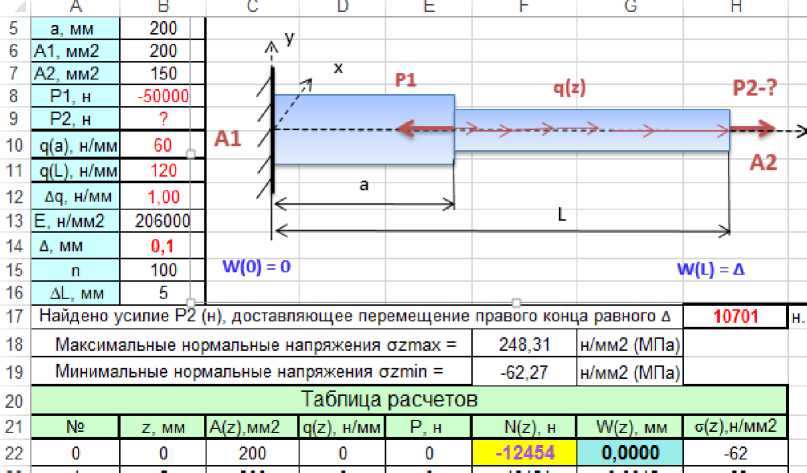
Рисунок 7. Продольное перемещение и реакция в опоре

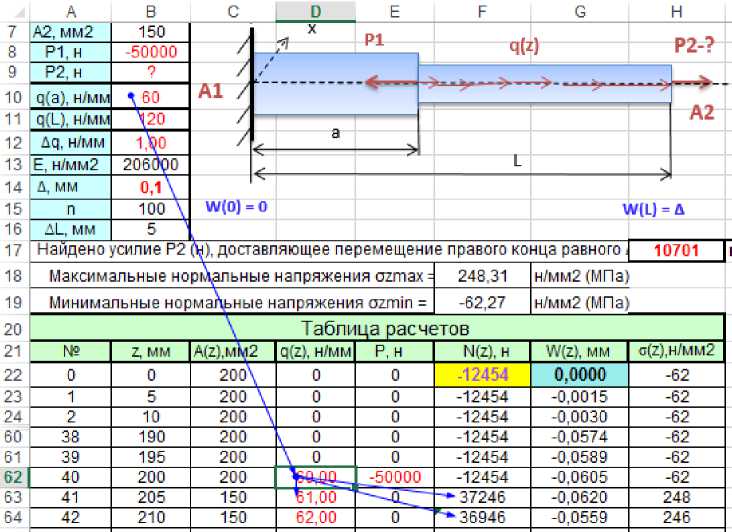
Рисунок 8. Распределение нагрузки по брусу

При вводе исходных данных построена диаграмма поперечного сечения рис. 6.

• -    заполняем данные электронной таблицы – на первом участке площадь поперечного сечения и на втором участке соответственно;

• -    на рисунке 8 через зависимые и влияющие ячейки видно рассредоточение распределенной нагрузки, начиная с принятой длины участка 200 мм (B10–D62), далее организовано приращение до значения = 120 Н×м;

  - шаг дифференцирования n=100 (В15);

  - столбец F, начиная с F22 приращение реакции опоры, в зависимости

от линейного размера бруса и действующих на него сил»

• -    Колонка q в таблице протянута до конца и в конце должна быть

величина 120, соответствующая длине 500 мм.

__ А

4 L, мм

В 500

5 а. мм

6 А1, мм2

7 А2, мм2

8    Р1, н

9   Р2, н

10 д(а), н/мм

11 q(L), н/мм

12 aq. н/мм

13 Е, н/мм2

-50000

P2-?

(1.00

lOOO

Условные обозначения

Математические зависимости

14 Д. мм

W(0) = о

w(l) = a

16 I 4L, мм

17 Найдено усилй^(н).до^вляющее перемещение правого конца равного] 10701

18 Максимальные н

!ьные напряжения azmax

248,31

н/мм2 (МПа)

19 Минимальные норм

!Ё№4гапряжрния azmin

-62,27

н/мм2 (МПа)

Z мм

60,00

61.00

,а расчетов

^®5

N(Z), Н

-12454

-12454

' \X454

W(Z), мм

0,0000

-0,0589

-0,0605

c(Z).H/MM2

1211    99

122 |   100

'20,00

-0,0620

1,1829

123|   №

Z мм

A(z),mm2

q(z), н/мм

W(z), мм

-(z).h/mm2

Рисунок. 9. Распределение нагрузки при Р 2 =0

• -    Показываем сосредоточенные силы Р₁(Е62), которая приложена в конце первого стержня

Формирование и поиск решения

При заданных условиях, что Р2 равна нулю должны добиться того, чтобы в сила N на диаграмма равнялась 0.

Исходя из построенных диаграмм видно, что перемещение свободного конца составит –0,1 мм.

Продольная сила на конце бруса, при длине его 500 мм будет равна 0

Ставим следующее условие: найти значение Р2, при ∆=0,1 мм (В14)

Необходимо записать значение Р2 в колонку внешних нагрузок, учитывать, что продольная нагрузка учитывает значение предыдущей нагрузки.

Принимаемая нагрузка для дальнейшего расчёта может быть заложена в ячейку Е120 (рис.11)

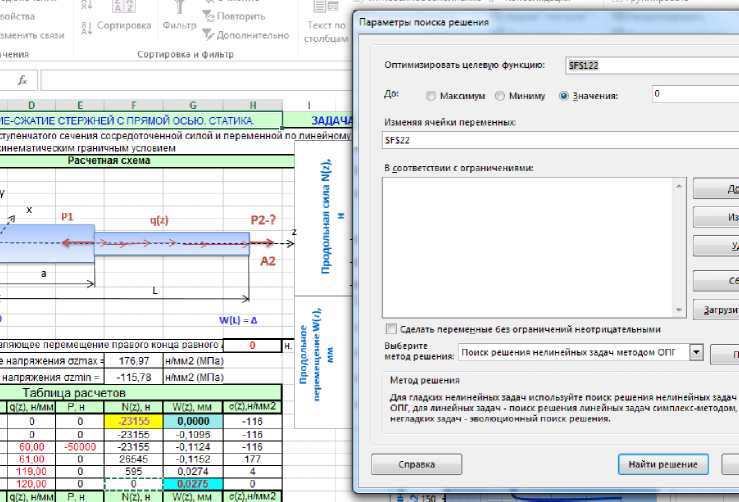
Рисунок 10. Параметры поиска решения

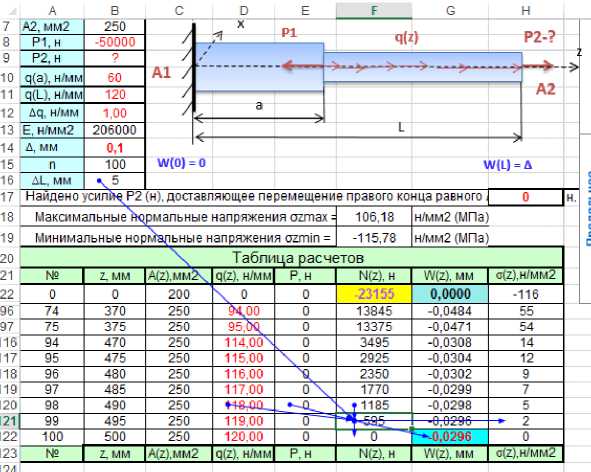
Рисунок. 11. Учет предыдущей нагрузки.

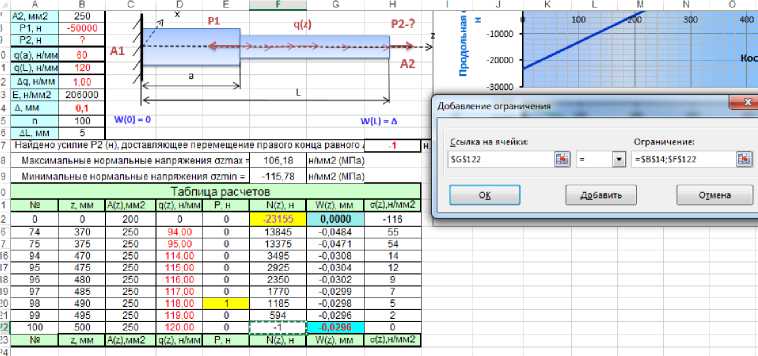
Таблица расчетов

A(z),mm2

q(a), н/мм q(L), н/мм

W(S. ММ 0,0000

N(z), н -23155

| А2, мм2

J Р1, н

3 Е, н/мм2

7 Найдено усилие Р2

iL, мм

(н), доставляющее перемещение правого конца равного^ 1   ~[н

Максимальные нормальные напряжения azmax

106,18

Минимальные нормальные напряжения ozmin

-115,78

95,00

117,00

н/мм2 (МПа)

н/мм2 (МПа)

-U;,h/mm2

-0,0299

0,0296

W(z), мм

g(z),h/mm2

Добавить |        | Отмена

W(O) = о

W(L) = Д

Добавление ограничения

Ограничение:

500      250

z мм A(z),mm2

120,00     0

дИ, н/мм| Р, н

N(z), н

’ | = SBS14;SFS122

Р2-?

Рисунок. 12. Нахождение силы Р 2 при ∆=0,1 мм

Активируем вкладку «Поиск решения».

Добавив все ограничения и ссылки соответственно на $G$122, задавая ограничения =$B$14; $F$122

Расчетная схема

L мм

6 А1 мм2

10 q(a). н/мм

2 Исходные данные

Растяжение-сжатие стержня ступенчатого сечения сосредоточенной силой и переменной по линейному закону 2 распределенной нагрузкой с кинематическим граничным условием

5 а мм

7 А2 мм2

8 Р1.н

9   Р2. н

224 52 н/мм2 (МПа)

Максимальные нормальные напряжения azmax = Минимальные нормальные напряжения ozmm =

11 q(L). н/мм

12 Дд н/мм

13 Е. н/мм2

14 Д мм

15 л

16 ЛЬ мм

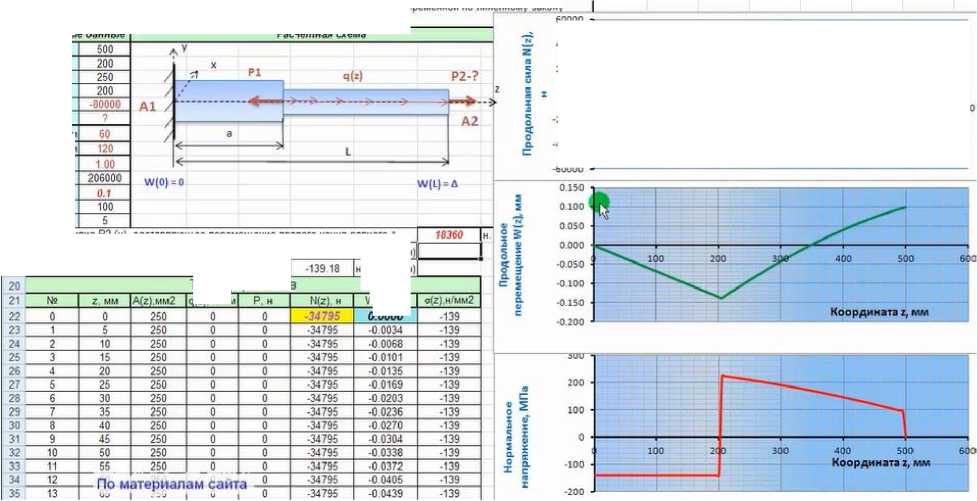
Таблица расчетов q(z) н/мм

Рисунок. 13. Окончательное решение

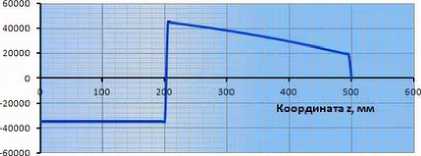
17 Найти усилие Р2 (н) доставляющее перемещение правого конца равного д

н/мм2 (МПа)

W(z) мм 0.0000

Сумма продольных сил на конце бруса (диаграмма продольных перемещений) равна 0.

Перемещение на конце бруса (диаграмма перемещений) = 0,1 мм

Сила Р2 (Н17) = 18360 Н.

Задача решена.