Автоматизация оцифровки и аппроксимации изображений графиков функций

Введение. Перед любым инженером или студентом технической специальности нередко возникает задача переноса данных графиков с бумажных носителей в цифровую систему. Введение данных вручную отнимает много времени и влечет за собой высокую степень погрешности.

Цель исследования. Стоит задача сформировать алгоритм, детектирующий координатные оси, точки графика функции и на их основе, строящий аппроксимирующий полином.

Первичная обработка изображения. Исходное изображение — это фотография графика на бумаге, пример на рисунке 1. Пользователь указывается рамкой первичную область поиска графика. Стоит увеличить контрастность и резкость изображения, чтобы были лучше видны координатные оси.

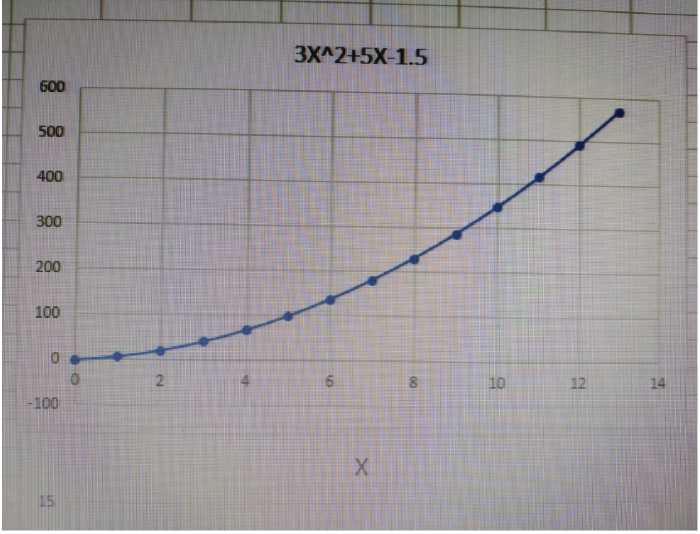
Рис. 1 Фотография графика

Вершины направляющих линий найдем следующим образом. Поиск начинается с левого верхнего угла изображения черных пикселей, самый первый является N-ой отметкой P n , запишем ее координаты на изображении как (0,0) используем поиск в глубину и составим скелет граничных точек.

Постоим вектор от Pn точки до каждой найденной по следующему принципу:

если существует непрерывная цепочка точек из исходного массива, то запишем координаты последней точки цепи как (0,1). Далее алгоритм разворачивается на 90 градусов и начинает поиск с крайней правой точки, ища направляющую оси абсцисс. В итоге мы получим область графика в прямоугольнике с координатами вершин, изображенных на рисунке 2.

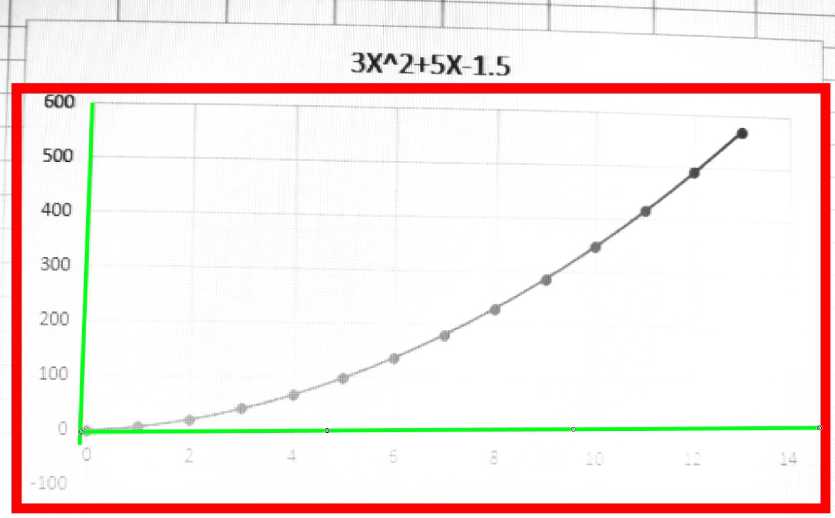
Рис. 2 Обнаружение осей графика

Поиск точек графика. Зная расположение осей в области поиска, удалим их из исходного массива пикселей, присвоим им значение 0 – белый цвет. В области поиска останется только погрешности фотографии и искомый график. Избавиться от погрешностей и случайных точек можно построив графы G = (V, Е). Каждая вершина V ,означает пиксель на изображении, а ребро Е = 1 (const). для каждого соседнего пикселя черного цвета. В итоге получим K графов, включающих в себя по N последовательно соединенных точек. [1] Найдем среди них MAX(G^ = {Max(G t ), i £ 1.. N; }. по количеству вершин. Далее используем алгоритм Краскала для поиска остовного дерева в графе G_max ., тем самым получим список L. всех пикселей, лежащих в области нашего графика, рисунок 3.

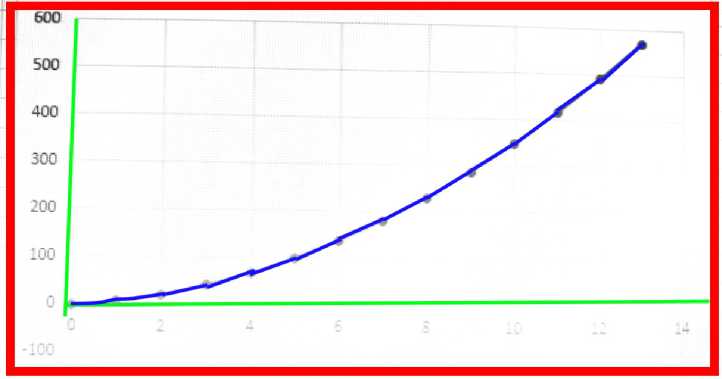
Рис. 3 Остовное дерево

Следующий шаг определение масштаба. Поскольку все наши точки лежат в области [0;1], то необходимо запросить у пользователя значение граничных меток на координатных осях ScaleX и ScaleY соответственно. Тогда координаты точки Р ^ в списке L будет определятся как Р ^ (%,у) = P_t(x * ScaleX;y * ScaleY); Сформируем матрицу М = {'TjVT j = P_t(x * ScaleX;y * ScaleY); i G 1.../V}, где N число пикселей в области поиска. Полученные данные не являются точными и могу содержать неровности и пробелы, рисунок 4. Необходимо аппроксимировать полученные данные и построить график аппроксимирующей функции.

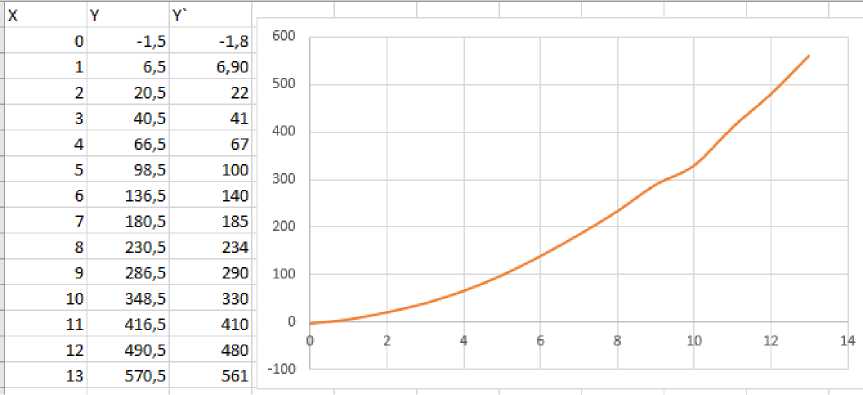
Рис. 4 График матрицы M

Аппроксимация. Способ аппроксимации будет выбран системой автоматически, как имеющий наименьшую погрешность. Рассмотрим в качестве примера метод наименьших квадратов [2]. Как видно на рисунке 5 мы получили следующий полином и построили его график. Полученные данные теперь можно экспортировать в удобную среду для расчетов.

Least-squares best fits:

-0.0725524 x⁴ + 1.43234 x³ - 6.62442 X² + 31.098 x - 24.4444 (quartic)

-0.308923 x³ +7.85498 x² - 17.2842 x + 28.9127 (cubic)

2.29437x2 + 12.4342 x- 15.9429 (quadratic)

Рис. 5 Варианты аппроксимирующих функций

Анализ погрешности показывает лучшую точность у полинома второй степени. Выберем его и построим график, рисунок 6.

Аппроксимирующая функция\Оригинал

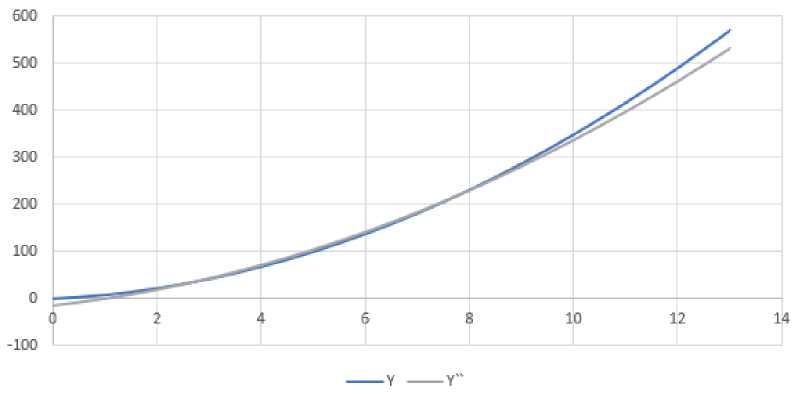
Рис. 6 Варианты аппроксимирующих функций

Заключение. По итогам проведенной работы мы получили алгоритм для автоматической оцифровки графиков функций и построения аппроксимирующей функции. Сложность алгоритма линейно зависит от размера изображения и его качества. Алгоритм требует доработки для изоляции шумов, погрешностей и ускорения быстродействия.