Автоматизация тепломассообменных расчетов в пористых вставках

В статье представлено общее описание и результаты подробного тестирования программного комплекса для решения системы нестационарных дифференциальных уравнений, описывающих сопряженный тепломассообмен в пористых телах в двумерной расчетной области произвольной формы. Рассмотрены составленные автором тестовые задачи.

This paper presents general description and results of detailed testing of program complex for solution of the whole system of nonstandard differential equations, describing conjugate heat and mass transfer in porous bodies in double-measured calculating area of free form. The author offers test problems worked out by him.

При анализе большого числа научных работ легко прослеживается тенденция все более частого использования разнообразных пористых материалов в теплообменных аппаратах. Значительное многообразие конструкций теплообменников [1] с пористым наполнителем и номенклатуры [2] пористых материалов не дают возможность выработать единую методику их расчета или выделить единый критерий для сопоставления. В то же самое время множество математических моделей гидродинамики и теплообмена в пористых средах позволяет получить надежные расчетные данные [1]. Поэтому возникает потребность в автоматизации таких расчетов и объединении различных математических моделей в одном программном комплексе. Эта задача была успешно решена в МГТУ им. Н.Э. Баумана. Созданный программный комплекс предназначен для решения системы нестационарных дифференциальных уравнений, описывающих сопряженный тепломассообмен в пористых вставках в двумерной расчетной области произвольной формы в декартовой или цилиндрической системах координат. При его тестировании были решены несколько составленных автором задач, имеющих аналитическое решение, часть из которых рассмотрены в данной статье.

Задача 1 . Изотермическая проницаемость через плоскую пористую стенку. Плоская пористая стенка толщиной δ имеет вязкостный α и инерционный β коэффициенты сопротивления. На левой границе стенки поддерживается давление воздуха P₁, на правой – P₂. Температура фильтруемого сквозь стенку воздуха Т неизменна. Необходимо определить распределение давления по толщине стенки и расход газа.

Для этого случая аналитическое решение для значений давления P при значениях координаты x определяется так:

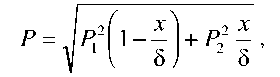
а для расхода газа G записывается следующее соотношение:

G

2в где μ – динамическая вязкость воздуха, R – универсальная газовая постоянная.

Задача 2. Изотермическая проницаемость через цилиндрическую пористую стенку. Цилиндрическая пористая стенка с внутренним радиусом r 1 и внешним радиусом r 2 имеет вязкостный α и инерционный β коэффициенты сопротивления. На внутренней и внешней поверхностях цилиндра поддерживается давление воздуха P 1 и P 2 соответственно. Температура фильтрующегося сквозь стенку воздуха Т неизменна. Определить распределение давления по радиусу цилиндра и расход воздуха.

При аналитическом решении расход газа G определяется так:

G =

—

αμr r ln

( - )

V ri j

2в(r2 — rl )

+

( -ац - riln —

V ri J 2e(—2 — rl )

+ —2 -, (Pi2 — P )

2 p RT(r2 — r,) ’

V             J а распределение значений давления P в зависимости от значения радиуса r описывается следующим выражением:

P2 = P2 — 2ац GRTln

< A

r

V rl J

— 2p G2 RT-

^— r i

rr

.

Важно отметить, что в математической модели для численного решения этой задачи учтено уравнение неразрывности.

Задача 3. Температурное состояние обогреваемой сплошной стенки с пористым охлаждением. Сплошная стенка толщиной h и длиной L покрыта с внешней стороны пористым каркасом длиной L и высотой δ. Схема расчетной области представлена на рис.1.

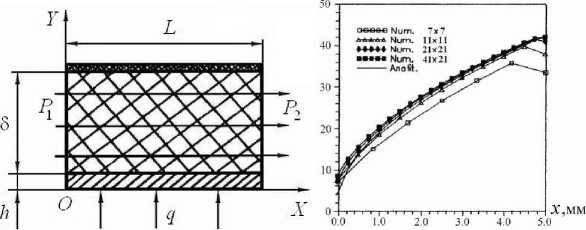
Рис.1. Расчетная область       Рис.2. Результаты решений для задачи 3                      задачи 3

Стенка нагревается продуктами сгорания с плотностью теплового потока q со стороны сплошной поверхности. Хладагент вводится в пористую вставку равномерно распределенным по поверхности, перпендикулярной направлению его движения. Расход хладагента G, плотность – ρ, теплопроводность – λG и теплоемкость – cp. Теплопроводность каркаса λ1 вдоль оси Oх и λ2 вдоль оси Оу. Гидравлическое сопротивление пористой вставки определяется вязкостным α и инерционным β коэффициентами сопротивления. Давление и температура хладагента на входе в пористую матрицу P1 и T1, давление его на выходе из пористой вставки – P2. Объемный коэффициент теплоотдачи от каркаса пористой вставки к хладагенту – αv. Необходимо рассчитать распределение температуры Tw на поверхности сплошной стенки, покрытой пористой структурой.

В этой задаче режим теплообмена можно считать форсированным [3], поэтому влияние продольного переноса теплоты теплопроводностью в пористой структуре и хладагенте можно не учитывать. В этом случае распределение температуры на поверхности сплошной стенки, соприкасающейся с пористой структурой, рассчитывается по известному уравнению [3]. Итоги численных решений задачи выявили хорошее соответствие с аналитическим решением, что показано на рис.2, отражающем результаты аналитического и численных решений с различным числом узлов в расчетных сетках.

Финалом тестирования работоспособности программного комплекса послужило сопоставление расчетных данных с результатами экспериментов. Для этого осуществлялось численное моделирование натурных экспериментов с пористыми вставками длиной 5 мм, 10 мм и 15 мм, показанными на рис.3.

Рис.3. Экспериментальные пористые образцы

Натурные испытания проводились на специализированном экспериментальном стенде. Вид экспериментальной установки приведен на рис.4. Конструкция экспериментального участка разработана автором и подробно описана в работе [4]. Расчетная область для задачи математического моделирования натурных экспериментов показана на рис.5. По границе FE подводится тепловой поток q, в области GHCD движется теплоноситель, на границе АВ учитывается теплообмен с окружающей средой, происходящий по закону Ньютона-Рихмана.

Удовлетворительное совпадение расчетных и экспериментальных данных окончательно подтвердило корректную работу программного комплекса, что позволяет в дальнейшем перейти от проведения довольно дорогостоящих огневых испытаний с использованием трудоемких в изготовлении экспериментальных образцов к численному моделированию процессов гидродинамики и теплообмена.

Рис.4. Экспериментальная установка Рис.5. Расчетная область

Более того, с помощью описанного программного обеспечения можно автоматизировать как расчет большинства параметров в прогнозируемой конструкции, так и выбор самой конструкции теплообменника еще на этапе его проектирования. Автоматизация расчетов всех параметров в теплообменных аппаратах любого вида позволяет существенно сократить материальные и временные затраты при их разработках, что прогнозирует значительный экономический эффект.