Автоматизированная модель статистического анализа в сравнительном подходе к оценке недвижимости
Автор: Ахметов О.А., Мжельский М.Б.
Журнал: Имущественные отношения в Российской Федерации @iovrf
Рубрика: Блокнот практика
Статья в выпуске: 10 (61), 2006 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/170151385
IDR: 170151385
Текст статьи Автоматизированная модель статистического анализа в сравнительном подходе к оценке недвижимости
В статье «Региональные базы данных для оценочной деятельности и их математическое обеспечение»1 рассматривались проблемы организации аналитического обеспечения практической деятельности оценщика. При этом были затронуты два основных вопроса:
-
1) наличие непротиворечивых стандартов и методик, достаточных для обеспечения обоснованности принимаемых на их основе решений, возникающих в процессе работы;
-
2) необходимость постоянного мониторинга и грамотной обработки рыночных данных.
Большая часть статьи была посвящена обсуждению первого вопроса. Рассмотрение второго вопроса в основном сводилось к формулированию задач, требующих скорейшего разрешения, в том числе статистическая обработка данных, включающих качественные (нечисловые) значения факторов, выявление достаточного количества ценообразующих факторов и т. д. В той же статье был приведен перечень обязательных задач, решение которых должно быть в определенной степени стандартизировано. К таким задачам относятся следующие:
-
• определение ценообразующих факторов по данным однородной выборки;
-
• определение значимости (весовых коэффициентов) факторов по данным однородной выборки;
-
• определение стоимости объекта оценки и арендных ставок с помощью многофакторных регрессионных моделей;
-
• определение ставки капитализации с помощью обработки баз данных рынка аренды и рынка продаж.
В настоящей работе рассматриваются некоторые способы решения, сформулированных нами задач.
Многофакторные регрессионные модели
Знание аналитических зависимостей между функцией и аргументами позволяет без труда отвечать на сформулированные выше вопросы. Но такие зависимости в явном виде для рынка коммерческой недвижимости получить практически невозможно, поэтому для нахождения аналитических связей используется регрессионный анализ. Однако прямое использование методов регрессионного анализа сопряжено с рядом трудностей: это и зависимость точности результата от оцифровки качественных факторов, и невозможность представить аналитически функциональную зависимость между факторами и значением функции, и т. д. С целью преодоления указанных проблем были использованы методы стохастического моделирования построения системы линейных регрессионных уравнений. В этом
Таблица 1
В качестве примера рассмотрим выборку по продажам складов в Кировском районе города Новосибирска (табл. 1).
Предположим, что по имеющимся данным необходимо построить систему регрессионных уравнений оценки стоимости складских помещений при условии, что максимальная ошибка не превысит 20 процентов. Результат представлен в таблице 3, на которой показано, что все множество представленных в выборке складских помещений оказалось разбитым на четыре группы, для каждой из которых получены соответствующие оцифровки нечисловых факторов и регрессионные уравнения.
Необходимо сделать одно существенное замечание. Использование метода стохастического моделирования, кроме очевидных преимуществ, имеет и негативные стороны. Так, при повторном построении системы уравнений мы можем получить (и, скорее всего, получим) другие уравнения и, возможно, другие интервалы разбиения, но при соблюдении обязательного требования к предельной ошибке результата. С этим приходится мириться хотя бы потому, что в предложенном методе моделирования находят отражение неопределенность и неоднозначность, являющиеся неотъемлемой частью рынка недвижимости.
Теперь оценим по выборке (табл. 1) стоимость одного квадратного метра площади продаваемых складских площадей, соответствующих первой строке выборки. Тогда оцифровка для такого объекта оценки будет выглядеть так, как показано в таблице 2.
Таблица 2
Оцифровка факторов для объекта оценки
|
Фактор |
Значение |
Оцифровка (модуль) |
X(i) |
|
Адрес |
Кировский район |
982,21897 |
X (1) |
|
Общая площадь, м2 |
3 600 |
11 212,74878 |
X (2) |
|
Теплое или холодное |
холодное |
1 277,92599 |
X (3) |
|
Техническое состояние |
удовлетв. |
968,56453 |
X (4) |
|
Подъездные пути |
авто |
770,68926 |
X (5) |
|
Наличие грузоподъемного оборудования |
есть |
4 849,13956 |
X (6) |
|
Наличие мощностей |
есть |
431,53185 |
X (7) |
Соответствующее уравнение удельной стоимости для оценки имеет следующий вид:
Y = –23 6619 776 933 434 + 181 957 253 237,387 X (1) – 0,27709 X (2) –
– 5,65428 X (3) – 181 957 253 297,091 X (4) + 100 033 254 058,914 X (5) + (*)
+ 0,67076 X (6) + 363 914 506 530,123 X (7).
Если подставить в полученное уравнение значения факторов (оцифровки), то стоимость одного квадратного метра площади рассматриваемого складского помещения будет равна 1 488 рублям. Ошибка составит 16 процентов, что ниже максимальной заявленной ошибки.
Несмотря на то, что регрессионное уравнение удовлетворяет наложенным ограни- чениям по точности, обращают на себя внимание неестественно большие значения коэффициентов при факторах и свободного члена. Это наводит на мысль о том, что приведенная выборка может содержать заведомо неценообразующие факторы, которые необходимо выявить и исключить.
Ценообразующие факторы
Анализ различных баз данных показал, что регрессионные уравнения принимают наиболее естественный вид в том случае, когда из всех факторов, включенных в выборку, учитываются лишь ценообразующие. Поэтому в самом начале работы с базой данных полезно определить список этих факторов.
Говоря о ценообразующих факторах, обычно имеют в виду те из них, влиянием которых на стоимость пренебречь нельзя. Иначе говоря, ценообразующие факторы в основном определяют значение и изменение величины стоимости объекта.
Поэтому определение ценообразующих факторов связано с изучением степени влияния конкретного фактора на изменение стоимости. Если говорить о регрессионных уравнениях, то это влияние описывается соответствующими коэффициентами при Хi . Следовательно, определение ценообразующих факторов из числа отслеживаемых в представленной выборке можно проводить по соответствующим регрессионным уравнениям. Нетрудно понять, что в регрессионном уравнении степень ценооб-разуемости характеризуется произведением коэффициента на соответствующее числовое значение фактора (далее – вклад).
Предлагаемый метод стохастического моделирования при оцифровке и построении регрессионных уравнений дает большой выбор регрессионных уравнений и, соответственно, множество значений интересующих коэффициентов. Соответственно, вклад характеризуется своим средним значением, средним квадратическим отклонением (СКО) и коэффициентом вариации (ν). Учитывая последнее замечание, в качестве критериев степени «ценообразуемости» можно выбрать следующие:
-
1) коэффициент вариации вклада не должен быть больше остальных;
-
2) среднее значение собственно вклада должно быть достаточно большим.
Смысл первого критерия состоит в том, что величина вклада при ценообразующем факторе не может сильно изменять свои значения. Это вызвано тем, что свойство ценообразуемости не связано ни с конкретными оцифровками факторов, ни с конкретными версиями уравнений. Следовательно, на первом этапе факторы, для которых соответствующие вклады имеют большие значения вариации (ν) (по крайней мере больше единицы), должны быть исключены из числа ценообразующих. Здесь же необходимо отметить, что если какой-либо фактор сохраняет постоянное или почти постоянное значение во всей выборке, то в системе уравнений метода наименьших квадратов главный определитель будет равен или практически равен нулю. А это неизбежно приведет к появлению коэффициентов, имеющих неразумно большое абсолютное значение и значение СКО. Указанное положение (очень большие значения коэффициентов и их СКО) также является поводом для исключения таких факторов.
Второй критерий определяет рейтинг цено-образуемости среди факторов, удовлетворяющих первому критерию. По своей сути такой рейтинг является вероятностным и определение этого рейтинга можно сформулировать несколько иначе: среди ценообразующих факторов наиболее значимым будет тот, вклад которого будет максимальным, но с учетом вероятности, как случайной величины. После того как среди рассматриваемых ценообразующих факторов выделен наиболее значимый, этот подход последовательно применяется для определения степени значимости остальных значимых факторов.
Таким образом, на множестве ценообразующих факторов определяется естественная упорядоченность по степени ценообра-зуемости. Этот рейтинг определяет важность факторов по отношению друг к другу, что может помочь при анализе допустимой ошибки, объединении оценок и т. д.
Вернемся к полученному нами результату и виду регрессионного уравнения применительно к продажам складских помещений. Как уже отмечалось, неудачный вид уравнения связан с тем, что среди факторов имеются факторы, не являющиеся ценообразующими для конкретной выборки. Это подтверждает проверка числовых значений критериев для вкладов: средних значений, СКО и вариаций факторов (табл. 4).
Таблица 3
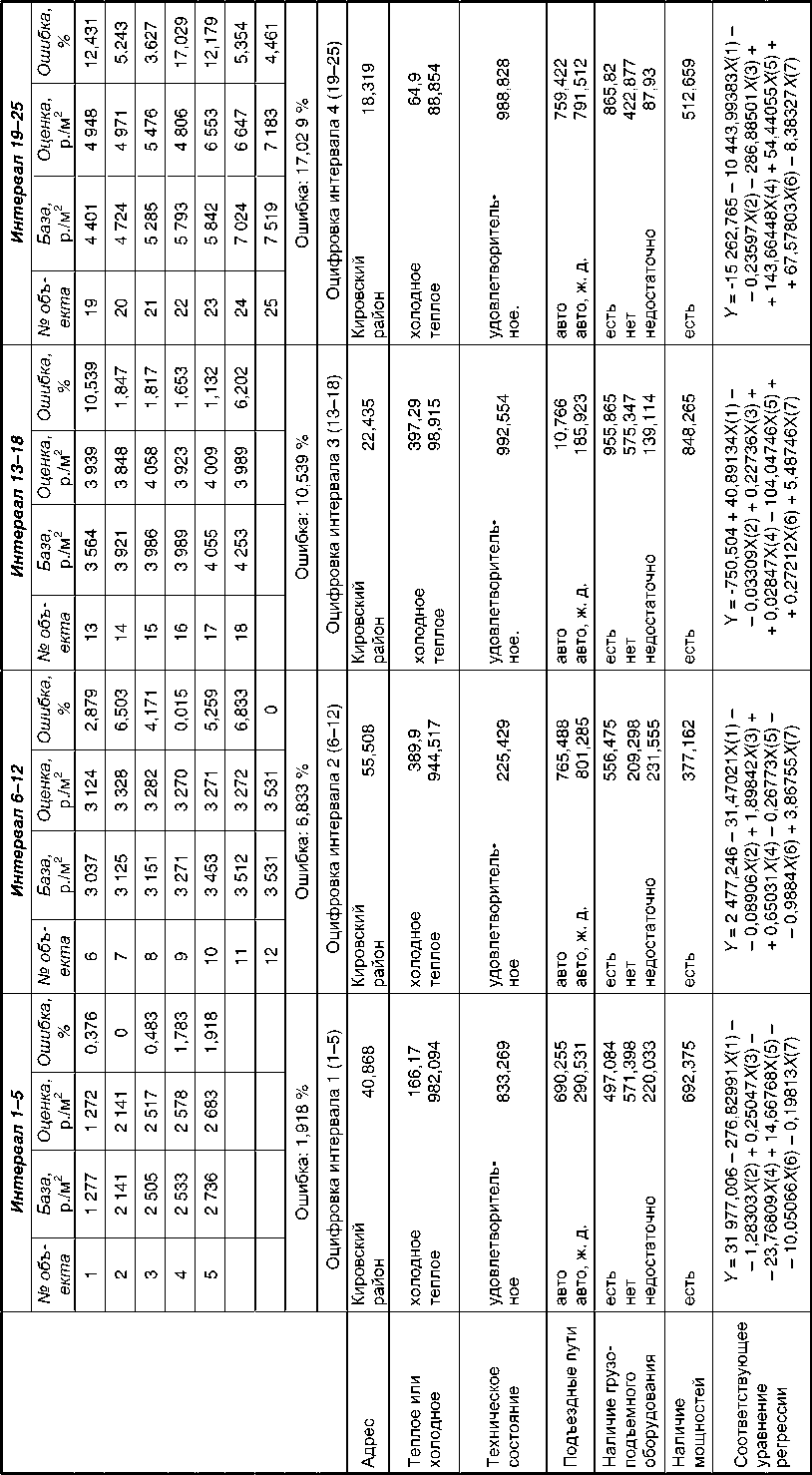
Таблица 4
Значение критериев рассматриваемых факторов
|
Показатель |
Адрес |
Общая площадь, м2 |
Теплое или холодное помещение |
Техническое состояние |
Подъездные пути |
Наличие грузоподъемного оборудования |
Наличие мощностей |
|
Среднее значение вклада |
1,79E + 14 |
3 106,957 |
7 225,747 |
1,76E + 14 |
7,71E + 13 |
3 252,629 |
1,57E + 14 |
|
СКО |
5,36E + 14 |
1 013,68 |
1 1567,41 |
5,29E + 14 |
2,31E + 14 |
1 856,772 |
4,71E + 14 |
|
Вариация |
3 |
0,326 |
1,601 |
3 |
3 |
0,571 |
3 |
Видно, что у четырех факторов вариация очень большая. Удаляя эти факторы, получим модифицированную выборку.
Тогда список факторов и их оцифровка будут выглядеть так, как показано в таблице 5.
Таблица 5
Параметры модифицированной выборки
|
Фактор |
Значение |
Оцифровка |
X(i) |
|
Общая площадь, м2 |
3 600 |
8 846,80799 |
X (1) |
|
Теплое или холодное помещение |
холодное |
4 409,47177 |
X (2) |
|
Наличие грузоподъемного оборудования |
есть |
3 850,18836 |
X (3) |
Оценка по модифицированной выборке стоимости одного квадратного метра площади продаваемых складских площадей, соответствующих первой строке базы данных, составит 1 295 рублей. Ошибка уменьшилась с 16 до 1,5 процента.
Повышение точности – не единственное преимущество, полученное посредством совершенного преобразования. По сравнению с вариантом (*) уравнение принимает гораздо более простой и естественный вид, а именно:
Y = 2 791,65551 – 0,45774 X (1) –
– 0,66508 X (2) – 0,83108 X (3).
Таблица, содержащая значения вклада, СКО и вариации для оставшихся факторов, тоже значительно упрощается (табл. 6).
Таблица 6
Параметры ценообразующих факторов
|
Показатель |
Общая площадь, м2 |
Теплое или холодное помещение |
Наличие грузоподъемного оборудования |
|
Среднее значение вклада |
4 049,573 |
2 932,665 |
3 199,809 |
|
СКО |
1 318,825 |
1 994,291 |
2 284,37 |
|
Вариация |
0,326 |
0,68 |
0,714 |
Как показывает коэффициент вариации, среди оставшихся факторов нет явных факторов, требующих удаления.
Хочется отметить еще одно свойство модифицированной базы. В курсе эконометрики указано, что в регрессионных линейных уравнениях коэффициенты при переменных имеют простой экономический смысл: они показывают изменение функции, приходящееся на единицу изменения данного аргумента. Но в любом учебнике написано, что свободный член уравнения, как правило, не имеет простого смысла. В случае оценки недвижимости мы имеем дело с приятным исключением: построив большое количество регрессионных уравнений для конкретного объекта и взяв из их числа среднее значение свободных членов, мы получим среднерыночное значение стоимости строительства одного квадратного метра площади для объектов, сведения о которых имеются в базе данных. Для приведенного примера многократное построение регрессионных уравнений (несколько тысяч) и усреднение значений свободных членов построенных уравнений дает оценку средней стоимости строительства одного квадратного метра площади складских помещений в городе Новосибирске, равную 7 400 р./м2.
Проверка выборки на нормальность
Важным элементом работы с выборкой является проверка на нормальность. Такая проверка повышает достоверность того, что полученная в дальнейшем оценка будет соответствовать стандарту. Сложность этой проверки, несмотря на большое количество разработанных в статистике критериев, состоит в том, что все значения стоимостей отнесены к разным объектам недвижимости, а на нормальность должно проверяться распределение стоимости (на конкретном рыночном сегменте), приведенное к одному объекту. В связи с этим перед проведением стандартных процедур по идентификации вида распреде- ления необходимо свести все разнообразие объектов недвижимости к одному конкретному объекту.
Выделим любой базовый объект с параметрами ( Xi0 ) и стоимостью ( Y0 ) и в соответствии с регрессионным уравнением ( Y0 )′= b + ∑ ai Xi0 . Выделим также произвольный объект параметрами ( Xi1 ) и стоимостью ( Y1 ). Тогда после приведения произвольного объекта к базовому получим величину стоимости произвольного объекта, если бы он обладал теми же свойствами как и базовый:
( Y0 )* = Y1 + ∑ a i ( X i 0 – X i 1 ).
Учитывая, что линейное преобразование не изменяет тип распределения, и убедившись, что после приведения всей выборки к базовому объекту стоимости последнего подчиняются нормальному распределению с заданным уровнем достоверности, можно распространить это утверждение на всю выборку. Причем нетрудно проверить, что последнее утверждение не зависит от базового объекта.
В качестве примера рассмотрим выборку по продаже складских помещений в Кировском районе города Новосибирска. В качестве базового элемента выберем первый элемент в выборке. Тогда пересчет стоимостей в соответствии с приведенными соотношениями даст последовательность стоимостей, представленную в таблице 7.
Предположим, что в качестве доверительного уровня (α) выбрано 95 процентов, тогда нетрудно определить остальные параметры статистического непараметрического критерия Уилкоксона (Вил-коксона). В этом случае критическое значение критерия Вилкоксона ( U α) равно 94, а соответствующее значение, полученное по выборке, равно 25. Это означает, что отвергнуть гипотезу о нормальном распределении на уровне 95 процентов нельзя (25 < 94). Практически можно принять, что стоимостные значения этой выборки подчиняются нормальному закону распределения.
Таблица 7
Проверка выборки на нормальность
|
Величины, соответствующие нормальному распределению |
Данные выборки |
||||||
|
1 |
1 020 |
13 |
5 286 |
1 |
2 103 |
13 |
4 789 |
|
2 |
1 835 |
14 |
2 805 |
2 |
2 779 |
14 |
1 875 |
|
3 |
1 715 |
15 |
3 123 |
3 |
2 733 |
15 |
2 024 |
|
4 |
1 937 |
16 |
2 145 |
4 |
-617 |
16 |
2 624 |
|
5 |
2 211 |
17 |
2 584 |
5 |
540 |
17 |
2 607 |
|
6 |
1 380 |
18 |
3 455 |
6 |
3 547 |
18 |
4 143 |
|
7 |
1 613 |
19 |
3 738 |
7 |
4 275 |
19 |
3 180 |
|
8 |
1 787 |
20 |
3 439 |
8 |
2 793 |
20 |
3 482 |
|
9 |
1 965 |
21 |
5 088 |
9 |
4 400 |
21 |
1 361 |
|
10 |
2 021 |
22 |
4 284 |
10 |
5 239 |
22 |
2 529 |
|
11 |
2 244 |
23 |
5 305 |
11 |
1 302 |
23 |
1 634 |
|
12 |
2 497 |
24 |
4 889 |
12 |
3 406 |
24 |
2 418 |


