Автоматизированное проектирование вычислительных сетей крупных проектных организаций

Проектирование сложных технических систем, таких как локальные, корпоративные и теле-коммуникационныевычислительныесети–слож-ный многоуровневый процесс. Он заключается в построении оптимальной системы, максимально использующей свои ресурсы. В процессе проектирования необходимо моделирование проектируемой сети для проверки ее эффективности и выявления ошибок. При моделировании действующей сети в процессе ее модернизации проектировщик обладает рядом статистических данных, после обработки которых, он может внести изменения в ее конфигурацию. При проектировании новой сети таких данных нет, и проектировщик может лишь предвидеть, прогнозировать, как будет загружен тот или иной сетевой канал, насколько велик будет объем вычислений, производимых тем или иным узлом сети. Подобные прогнозы представляют собой некоторые лингвистические формулировки, которыми можно оперировать, используя аппарат нечетких вероятностных величин. В процессе проектирования необходимо учесть и будущее назначение сети, для чего нужно построить имитационную модель тех процессов, которые будут в ней происходить. Только осознавая круг задач проектирования сети, можно построить ее наиболее эффективно. Модель прикладного уровня должна содержать прогнозные данные о сети, которые используются при ее дальнейшей оптимизации.

Первоначально необходимо создавать проект сети с возможностью моделировать и оптимизировать его до того, как начаты работы по созданию физической сети. Однако среди существующих программных пакетов не представлены подобные решения. Не осознан до конца и сам процесс подобного проектирования, его этапы и методика. Основные методы моделирования и перестроения сетей построены на том, что с существующей сети путем многократных статистических измерений снимаются данные о трафике, вычислительной загрузке узлов. Затем эти данные анализируются, и эксперт выдает рекомендации по перестроению отдельных сегментов или всей сети в целом. Зачастую в этом процессе не учитывается структура потоков данных на предприятии, структура его прикладных процессов, которые и являются основными источниками трафика и вычислительной загрузки системы. Кроме этого, при проектировании сети с нуля измерений для анализа не имеется, и проектировщик может оперировать лишь прогнозами. Следовательно, необходимо в систему проектирования вводить описания прикладных процессов, которые позволят даже на основании прогнозных данных вырабатывать оптимальные решения.

Обзор состояния исследований

В литературе моделирование вычислительных сетей рассматривается с нескольких точек зрения. С одной стороны моделируется структура вычислительной сети при помощи языков имитационного моделирования (ИМ). Отдельно описываются модели рабочих станций, файл-серверов, коммутаторов и концентраторов. Применение ИМ позволяет изучить их поведение как отдельно взятых объектов.

Исследования, связанные с математическим моделированием вычислительных сетей, в основном направлены на изучение какого-либо одного параметра сети. Обычно это надежность, отказоустойчивость и трафик. В моделировании надежности применяется теория графов [2-7]. Использование нечетких величин при моделировании трафика рассмотрено в работах [1; 10].

Исследование потоков данных на сегодняшний момент существует как отдельный аспект моделирования вычислительных сетей. Моделирование потоков и их динамики производится путем составления и решения систем дифференциальных уравнений. Этот вопрос освещен в работах [3; 8].

Трафик как нечеткая вероятностная величина

Основными характеристиками для сети являются трафик и вычислительная загрузка узлов. Трафик указывает на количество передаваемой по каналам сети информации, а вычислительная загрузка – на занятость вычислительной машины как узла сети.

Необходимо учитывать нечеткую и вероятностную природу этих двух параметров. Когда речь идет о проектировании сети с чистого листа, сетевой администратор не обладает никакой информацией о трафике и вычислительной загрузке и работает в условиях полной неопределенности. Однако он может делать прогнозы трафика и вычислительной загрузки для каждого из будущих узлов сети. Трафик и вычислительная загрузка как физические величины по природе своей непостоянны и зависят от множества внешних и внутренних факторов. В связи с этим, оценивать трафик в единичный момент времени нельзя; можно лишь давать интервальную, нечеткую оценку, оперируя такими нечеткими понятиями как «трафик высокий» или «трафик низкий». В том же случае, когда человек не просто оценивает трафик существующей системы, а прогнозирует его значение в условиях неопределенности, нечеткой оценки недостаточно; необходимо и к ней добавить вероятностную оценку. Например, наиболее приближенными к реальным условиям проектирования будут прогнозы вида «трафик скорее высокий» или «трафик точно низкий». Первое слово в подобном прогнозе отражает вероятность, а второе – интервальную оценку прогноза трафика или вычислительной загрузки.

Математически обрабатывать такие вероятностные нечеткие величины возможно с использованием математического аппарата, предложенного в работах [9, 11].

В общем случае дискретная нечеткая случайная величина (НСВ) имеет вид:

Поскольку при проектировании вычислительной сети человек выдает прогноз с помощью лингвистического термина, набор вероятностей P 1 , P ₂ ,....P _n можно также перевести в лингвистическую форму. Для этого вводится понятие «степень уверенности НСВ». Каждый вектор вероятностей кодирует степень уверенности НСВ, которая представляет собой лингвистическую оценку вида «точно», «скорее всего» («скорее»), «наверное» («возможно»). Каждую такую оценку можно представить в виде функции распределения НСВ.

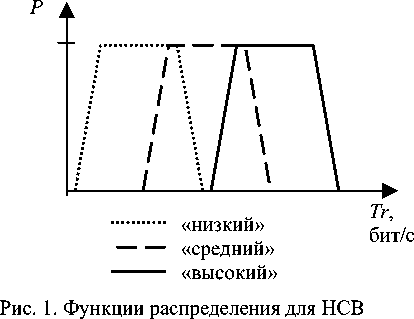
В данной работе принято три нечетких значения сетевого трафика: «высокий», «средний» и «низкий», которые определяются трапецеидальными функциями принадлежности. В связи с этим трафик можно записать так:

Tr = {" низкий" / P 1 ," средний" / P 2 ," высокий" / P 3 }

Здесь нечеткие множества заданы трапецеидальными функциями распределения (см. рис. 1). Причем основные параметры функций принадлежности задаются экспертно.

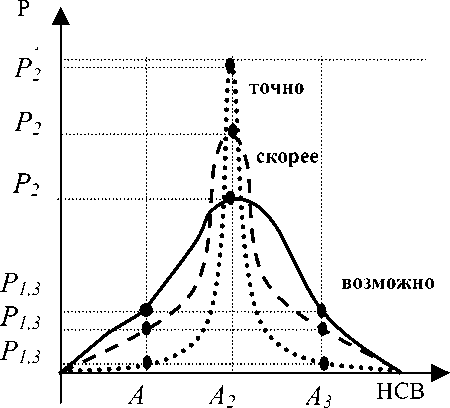
Рис. 2. Представление степени уверенности для 3-х значной СВ

Степень уверенности кодируется в этом случае, как указано рис. 2, векторами вероятностей, представленными в таблице 1.

Методика проектирования ВС

Начинать проектирование следует с создания функциональной модели прикладных процессов сети. Параллельно создается структурная модель сети; затем происходит слияние двух этих моделей с целью получения оптимального проектного результата.

Таблица 1. Представление векторов вероятностей

Степень уверенности НСВ	низкий	средний	высокий
«точно»	{1,0,0}	{0,1,0}	{0,0,1}
«скорее»	{0.75,0.25, 0}	{0.125, 0.75, 0.125}	{0,0.25, 0.75}
«возможно»	{0.5, 0.35, 0.15}	{0.25,0.5,0.2 5}	{0.15, 0.35, 0.5}

Для функционального моделирования прикладных процессов выбран язык потоковых диаграмм Data Flow Diagram, для которого предложен ряд дополнений. Поскольку любой узел сети работает как генератор сетевого трафика и вычислительной загрузки, то из всех сущностей языка DFD предлагается использовать только сущность «процесс» (рис. 3).

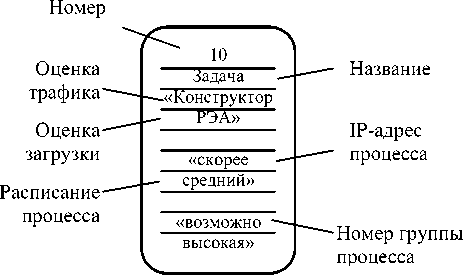
Рис. 3. Изображение процесса DFD

К ее обычным свойствам необходимо добавить нечеткие вероятностные оценки сетевого трафика и вычислительной загрузки, а так же расписание работы данного процесса. Последнее является необходимым в связи с тем, что узлы сети генерируют трафик непостоянно; их сетевая и вычислительная загруженность привязана к временным интервалам, связанным с режимом работы данного рабочего места.

Структурная модель вычислительной сети формируется диаграммой, где присутствуют такие категории как «узел», «коммутатор», «концентратор», «маршрутизатор».

Слияние функциональной и структурной моделей на основе генетической оптимизации

Слияние функциональной и структурной моделей проектируемой сети предлагается производить методом стандартного генетического алгоритма (СГА) для получения оптимального результата уже на начальных стадиях проектирования.

Хромосома для данного приложения СГА состоит из двух частей – изменяемой и неизменяемой. В качестве изменяемой части выбрана кодировка структурной модели, а в изменяемой части кодируется функциональная модель. Фактически СГА отыскивает оптимальное расположение блоков спроектированной функциональной диаграммы на структурной модели сети.

Расчет качества каждой хромосомы как варианта слияния функциональной и структурной моделей производится при помощи имитационного моделирования. В каждом случае прорабатывается вероятностная составляющая суммарной оценки трафика или вычислительной загрузки сети.

Целевая функция СГА является аддитивной и состоит из трех слагаемых:

F = График + F B3 + F rp

Первая часть целевой функции отвечает за распределение трафика:

F_трафик = m _i in ma _j x Tr_i^j , где i – номер текущей хромосомы СГА, j – номер сетевого канала, а Tr – суммарный трафик на одном канале.

Вторая часть функции отвечает за распределение вычислительной загрузки в сети:

FВЗ = min maxVzij , ij где i – – номер текущей хромосомы СГА, j – номер узла сети, Vz – – суммарная вычислительная загрузка на узле сети.

Третья часть целевой функции отвечает за качество группировки блоков диаграммы на физической структуре сети. Вычисление F гр происходит в несколько этапов. Вначале определяется общее количество групп, заданных проектировщиком – i. Затем для каждой из групп строится массив IP-адресов. В этом массиве вычисляется максимальное количество повторяющихся элементов – N _i . Значение F гр вычисляется как:

∑ N i

Fгр = i , общ где - Nобщ – общее число узлов сети.

Наиболее удобной реализацией предлагаемой методики проектирования является возможность параллельного проектирования функциональной и структурной модели.

Программная реализация системы проектирования и моделирования ВС

Интерфейс системы состоит из двух графических редакторов. В первом создается функциональная модель прикладных процессов, происходящих в сети. Пользователю дается возможность расставлять блоки на рабочем поле, соединять их потоками, а так же указывать прогнозные оценки трафика и вычислительной загрузки (ВЗ). Здесь же проектировщик формирует расписание работы каждого узла в отдельности.

Параллельно производится работа во втором графическом редакторе, предназначенном для построения структурной модели физической сети. Здесь проектировщик выстраивает узлы, коммутирующие элементы и маршрутизаторы, соединяя их каналами. Здесь же отлаживается таблица маршрутизации. Как и при построении реальной сети, администратор назначает каждому проектируемому узлу свой IP-адрес c назначением основного шлюза. На маршрутизаторах выстраивается таблица маршрутизации. Корректная настройка маршрутизации очень важна, так как она используется при трассировке связей DFD-диаграммы по физической модели сети.

Финальным этапом построения проекта сети является поиск оптимального расположения узлов диаграммы прикладных процессов по структуре физической сети при помощи стандартного генетического алгоритма (СГА). В системе имеется возможность настройки СГА по параметрам размера популяции, порога стабильности и количества шагов эволюционного времени. Хромосомой для СГА является единичный вариант расположения блоков диаграммы процессов относительно узлов проектируемой сети. Алгоритм работы СГА представлен на рис 4.

При работе СГА качественный параметр хромосомы тем лучше, чем он меньше, то есть F ¹ → min . Оценка качества хромосомы происходит по алгоритму, представленному на рис 5.

Таким образом, СГА осуществляет поиск того варианта, в котором сетевой трафик и вычислительная загрузка узлов наиболее распределены по системе.

Адаптация СГА к данной задаче заключается в построении хромосомы. В реализованной системе хромосома состоит из 2-х частей – изменяемой и неизменяемой. В неизменяемой части по порядку указаны порядковые номера узлов сети, назначающиеся системой автоматически. В изменяемой части хромосомы располагаются порядковые номера блоков бизнес-диаграммы. Операции рекомбинации и мутации производятся с изменяемой частью, причем в процессе обработки популяции перед расчетом качества хромосом происходит их проверка на корректность. Поскольку блоки диаграммы являются уникальными – их повторение в изменяемой части хромосомы недопустимо. Проверка на корректность отсеивает те хромосомы в изменяемой части, в которых присутствуют повторяющиеся блоки. При начальной генерации популяции так же происходит отсеивание таких хромосом.

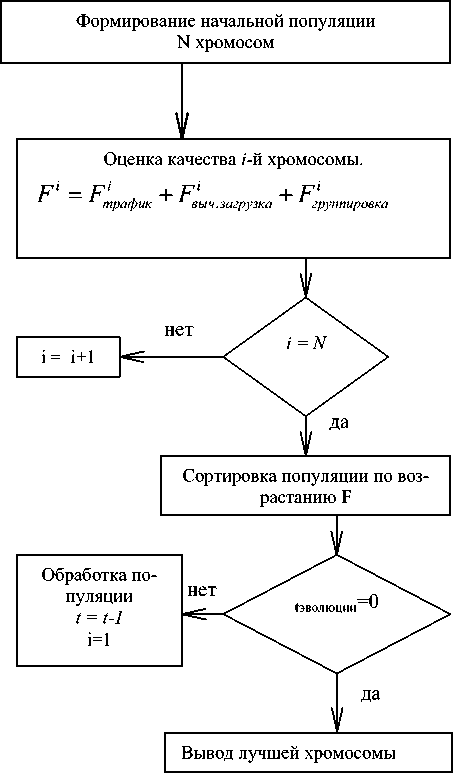
Рис. 4. Стандартный генетический алгоритм

Программная реализация построена с использованием объектно-ориентированного программирования.

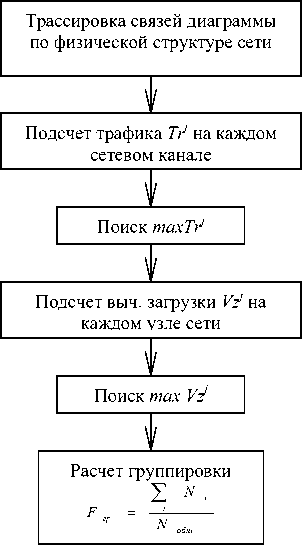
Рис.5. Алгоритм СГА

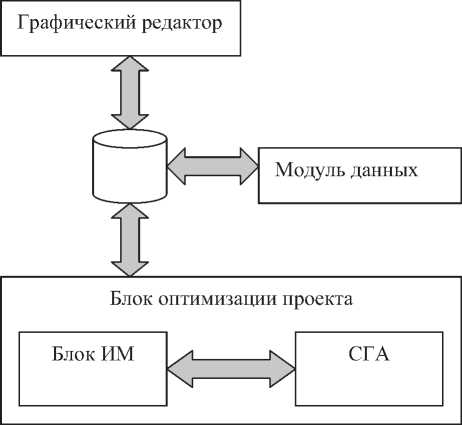
Рис. 6. Общая структурная схема программы

Интерфейс построен на основных визуальных компонентах Windows в среде Delphi 5.0.

Оценка результатов моделирования реальной ВС на основе разработанного программного инструментария

Примером моделирования послужила ВС крупного проектного предприятия. ОАО Ульяновское конструкторское бюро приборостроения (УКБП) – крупное предприятие, имеющее локальную сеть на 300 вычислительных машин. При помощи предлагаемой САПР ВС было произведено начальное проектирование корпоратив- ной вычислительной сети, а затем в связи с быстрым ростом числа приобретаемых предприятием компьютеров и полное перепроектирование.

Во всех вычислительных экспериментах СГА находил решение с одним и тем же значением целевой функции. Результирующий график сходимости СГА приведен на рис.7. Эксперименты по эволюционному поиску проводились на типовом компьютере класса Pentium 4 с частотой процессора 2200 Мгц, и объемом оперативной памяти 256 Мбайт. Длительность расчетов приведена в таблице 2.

Таблица 2. Длительность вычислительных экспериментов

Параметры СГА	Время оптимизации
P=100, Элита=10,Мутация 0,9	2 мин
P=500, Элита=100, Мутация 0,4	11 мин
P=5000, Элита =2000, Мутация 0,4	2 ч 20мин
P=100, Элита=10, Мутация 0,4	2 мин
P=10000, Элита=3000, Мутация 0,4	14 ч 40 мин
P=50000, Элита=5000, Мутация 0,5	34 ч 20 мин

При помощи созданного программного средства была произведена оптимизация проекта сети ОАО «УКБП» с выдачей рекомендаций по внесению в него соответствующих изменений. Существующая корпоративная ВС была описана на входном языке программной системы, в которой было произведено несколько вычислительных экспериментов.

Оптимизация выполнялась с различными наборами параметров СГА, для каждого из которых снимались показатели сходимости. Кроме этого снимались временные затраты на проведение этапов оптимизации.

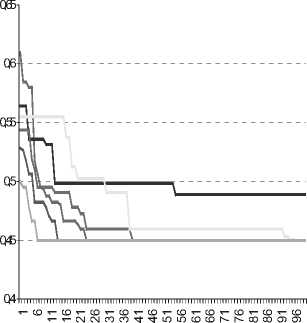
Рис. 7. Результаты эволюционного поиска для проекта сети ОАО «УКПБ»

Полученный в результате обработки проект сети ОАО «УКБП» был предложен в качестве исходного для дальнейшего развития и модернизации реально существующей сети.

Заключение

Автоматизированное проектирование ВС требует в качестве обязательной компоненты моделирования сети. Сеть представляет собой топологию узлов, каналов и коммуникационного оборудования. Природа трафика – нечеткая случайная величина. Взаимодействие узлов на прикладном уровне описывается на уровне прикладных процессов, например модифицированными DFD-диаграммами (дополненными расписанием работы ВС).

Для решения задач АП важны задачи оптимизации, в частности эффективна генетическая оптимизация для генерации транспортной схемы ВС, достаточной для организации процессов прикладного уровня.