Автоматизированное решение задачи размещения балансировочных грузов в отсеках космических аппаратов

Необходимость обеспечения минимальных отклонений массово-центровочных и инерционных характеристик (МЦИХ) космических аппаратов (КА) от заданных значений часто приводит к необходимости перекомпоновки бортовой аппаратуры (БА) и грузов в отсеках. Однако далеко не всегда удаётся обеспечить допускаемые отклонения центра масс (ЦМ) изделия за счёт рационального размещения БА и грузов, поэтому приходится проводить его балансировку при помощи добавочной балансировочной массы, являющейся совокупностью балансировочных грузов (БГ) разной конфигурации.

Поскольку процесс решения задачи размещения БГ и последующей оценки МЦИХ изделия довольно длительный и рутинный, целесообразна автоматизация этого процесса для повышения производительности труда инженера-конструктора.

Для этого в РКК «Энергия» была разработана и до недавнего момента использовалась, при участии автора, программа «Автоматизированная система балансировки изделия» для спускаемых аппаратов (АСБИ СА). Однако при попытке переноса программы на операционную систему (ОС) Windows 2010 и тестировании программы выяснилось, что она способна корректно функционировать лишь на устаревшей ОС Windows XP 2001. Вслед за этим был установлен факт утраты документации на АСБИ СА, где могли быть описаны математическая модель и метод решения задачи размещения БГ на лобовом теплозащитном экране (ЛТЭ) и между металлическими оболочками днища СА, а также листингов исходного кода программы.

Цель настоящей статьи — описание процесса воссоздания математической модели и программного обеспечения взамен устаревшей программы АСБИ СА с обобщением методики автоматизированного решения задачи размещения БГ для различных КА.

В рамках данной работы описаны математическая модель и метод решения задачи размещения БГ. Для верификации модели использовались фактические результаты балансировки ряда СА транспортного пилотируемого корабля (ТПК) «Союз МС». Программная реализация алгоритма осуществлена при помощи MS Office Excel 2010 , написан код для макросов фильтров, приведены фактически полученные результаты расчётов, их сравнение со значениями исходной версии программы АСБИ СА, приведён анализ причин расхождения результатов и путей достижения лучшей сходимости.

Общие сведения

Существует два основных вида балансировки: статическая и динамическая . Целью статической балансировки для КА, снабжённого двигателем, является совмещение ЦМ с продольной осью, совпадающей с линией результирующей тяги, чтобы обеспечить лучшие манёвренные возможности системы. Целью динамической балансировки КА является совмещение главных осей инерции с геометрическими осями изделия, чтобы минимизировать моменты дисбаланса от вращения и колебаний конструкции [1].

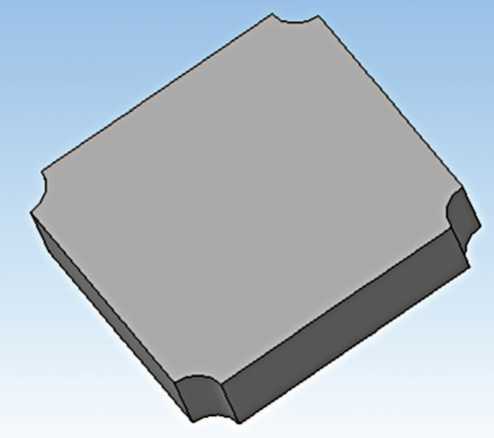
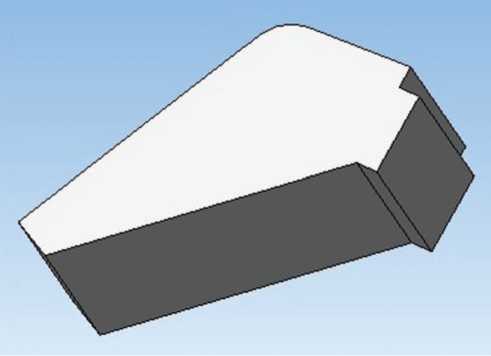
Балансировочные грузы представляют собой свинцовые квадратные или прямоугольные плитки с обратными вырезами в вершинах под конструкционные отверстия для базирования в случае клеевого соединения или для закрепления в случае болтового соединения, как показано на рис. 1. Альтернативным вариантом БГ могут быть более тяжёлые отливки с кронштейнами для их установки. Производятся БГ преимущественно штамповкой или литьём [2].

а)

б)

Рис. 1. Примеры твердотельных 3D-моделей балансировочных грузов: а — балансировочный груз на сферической части лобового теплозащитного экрана; б — балансировочный груз в зоне стыка лобового теплозащитного экрана с обечайкой корпуса спускаемого аппарата (рисунок создан автором)

Стоит отметить, что в ряде случаев ЦМ отсека КА может находиться вне продольной геометрической оси (например, у СА ТПК «Союз МС»,

КА «Фотон-М») для обеспечения специальных аэродинамических, термодинамических, гравитационных либо электромагнитных требований [3].

Кроме того, распределение балансировочной массы в выбранной зоне размещения должно обеспечить равно-прочность конструкции, а её количество не должно превышать допустимой доли от резерва главного конструктора. Это контролируется при разработке расчёта масс, центров масс и моментов инерции КА с подробной разбивкой по БА. В исключительных случаях балансировочную массу возможно включить в состав изделия за счёт снижения массы полезной нагрузки [4].

Математическое обеспечение

Существуют две основные концепции моделирования задачи размещения БГ в отсеке. Первая основывается на том, что массы БГ заранее стандартизованы и известны, поэтому необходимо определить координаты ЦМ БГ для монтажа. Вторая концепция основывается на том, что координаты ЦМ БГ заранее стандартизованы и известны, так что необходимо выбрать минимальное количество мест для их установки и подобрать массы.

Для решения задачи моделирования на основе первой концепции используются метод перебора компоновок [5], метод случайного поиска [6], маршевый метод смещений [3], метод базирования по направляющим [7]. Они являются численными методами расчёта координат ЦМ БГ.

При неавтоматизированном решении задачи большей популярностью пользуется вторая концепция по той причине, что она менее трудоёмкая. Её применение эффективно в случаях, когда предприятие занимается серийным выпуском КА, когда общая компоновка одного изделия слабо отличается от компоновки другого. Возможность предусмотреть в каждом случае стандартную зону размещения БГ позволяет впоследствии разработать типовой процесс монтажа БГ. Из таких соображений этот подход имеет приоритет и в данной работе. При реинжиниринге кода исходной версии программы АСБИ СА было выяснено, что именно вторая концепция была заложена в алгоритм решения задачи.

Если координаты ЦМ БГ стандартизованы, а их порядковые номера привязаны к массам, то математическая модель балансировочной массы может быть представлена в виде задачи линейного программирования.

В качестве целевой функции принимается сумма масс БГ, для которой нужно минимизировать функционал:

^N БГ

^M БГ = E m БГ j ^ ^{min, (1)} j = 1

где j — порядковый номер БГ, j = 1, N _БГ ; N _БГ — максимально возможное количество БГ; m _{БГ j} — варьируемая масса БГ.

В качестве краевых условий рассматриваются ограничения по массам БГ (2) и по центровке КА (3) в виде соответствующих неравенств:

0 ≤ m _{БГ j} ≤ max m _{БГ j} ,

где max m _{БГ j} — максимальная допускаемая масса j -го БГ;

N _БГ

T T

КА rКА = mБГj rБГj min TКА <--------Nr------^ max Ta’ (3)

MКА + E m бгj j = 1

где M _КА — масса КА без БГ; г К _А — вектор координат ЦМ КА, г КА = [ x _КА у _КА z _КА ]^Т; г БГ . — вектор координат ЦМ БГ, ⁷ БГ = ^[ x БГ У БГ z БГ^ min ⁷ КА и max ⁷ КА — векторы граничных допускаемых значений координат ЦМ КА.

Задача линейного программирования решается любым подходящим численным методом. Так, в исходной версии программы АСБИ СА использовался многопараметрический метод Ньютона [8], основная формула которого выражается следующим образом:

[ m БГ j ]^T k +1 = [ m БГ j ] k ^T – H k ^–1( M БГ ) ∇ k ^T( M БГ ), (4) где k = 1, 400 — порядковый номер расчётной итерации; H_k ^–1( M _БГ ) — обратная матрица Гёссе целевой функции; ∇ _k ^T( M _БГ ) — оператор набла целевой функции.

Следует отметить, что при переносе программы на современную ОС для решения задачи был выбран симплекс-метод, так как из стандартной библиотеки решателя ( Solver ) метод Ньютона был исключён её разработчиками.

Программное обеспечение

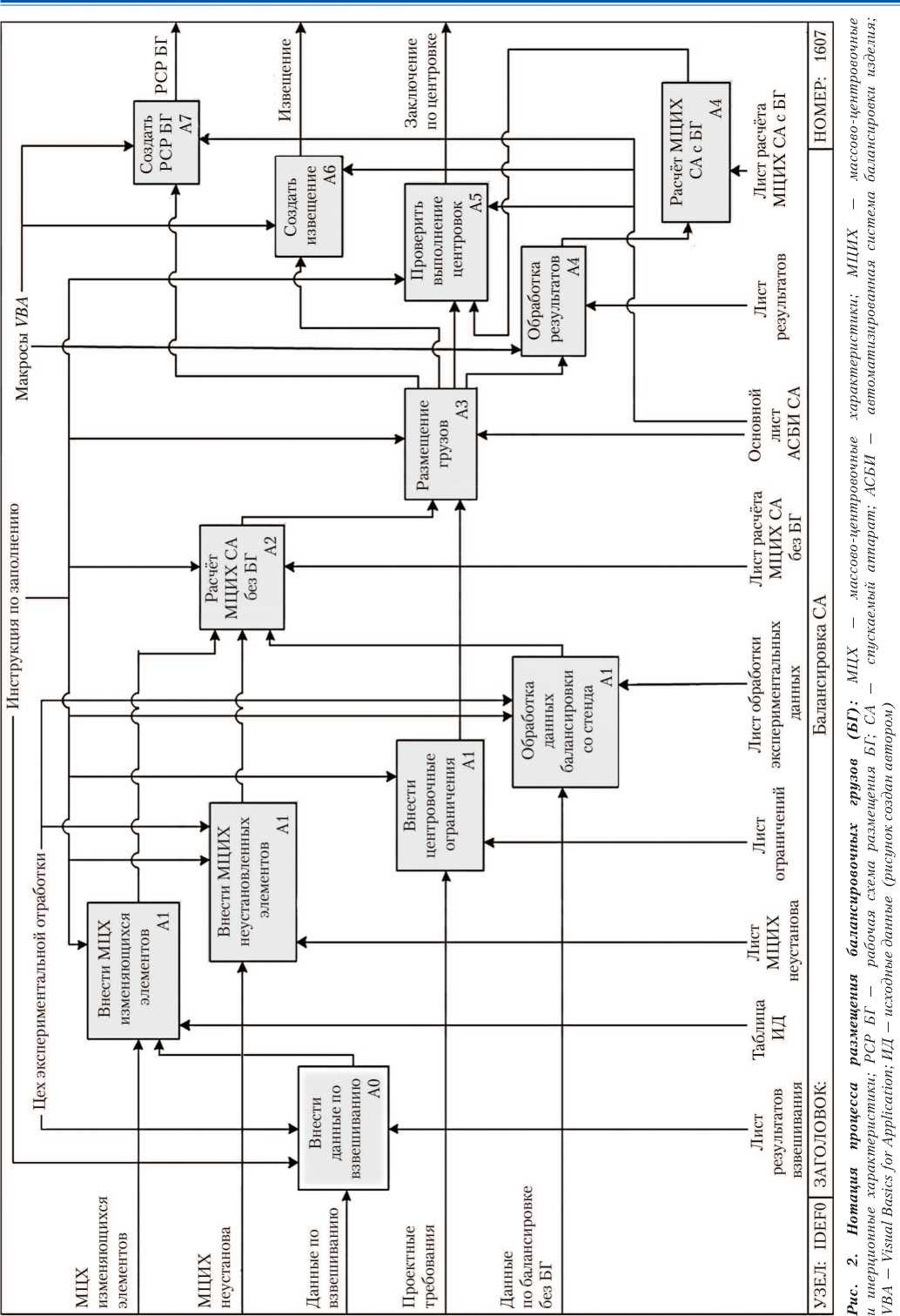
Программная реализация алгоритма решения задачи размещения БГ, а также расчёт масс, центров масс и моментов инерции для АСБИ СА были восстановлены средствами MS Office Excel 2010 с поддержкой макросов на языке программирования Visual Basic . Логика работы программы и маршруты обмена данными между разными стадиями процесса общего решения задачи балансировки представлены на рис. 2.

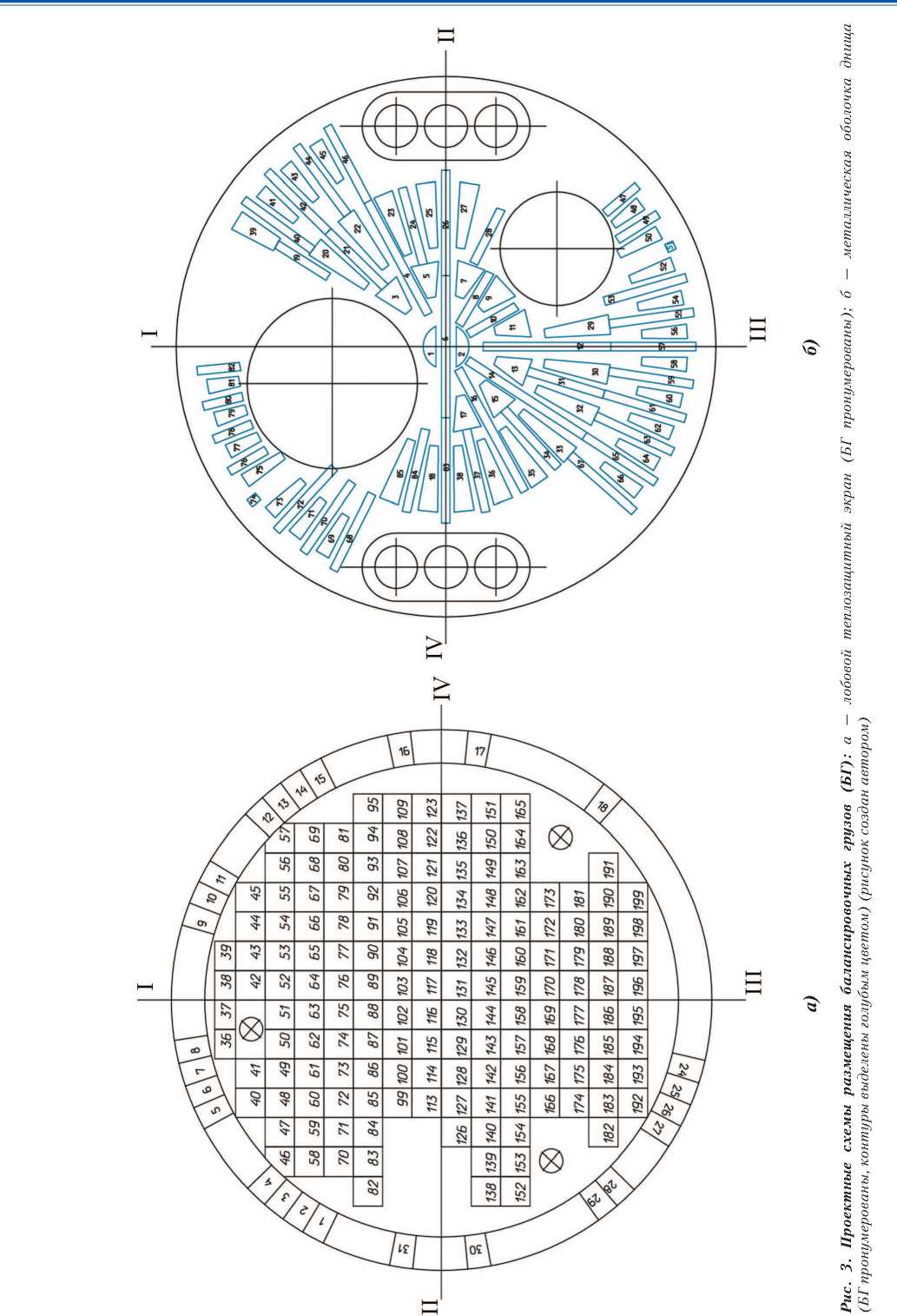
Виды проектных схем размещения БГ на ЛТЭ СА и между металлическими оболочками днища показаны на рис. 3. Их генерация возможна, если не заблокированы библиотеки AutoCAD 2013 Type Library и AutoCAD Focus Control for VBA Type Library. Также был восстановлен фильтр, который «подрезает» некоторые взятые БГ в соответствии со следующими условиями:

	/ 0, если 0 ≤ m БГ j ≤ 0,3;
m БГ j =	m БГ j , если 0,3 ≤ m БГ j ≤ max m БГ j – 0,3;        (5)
	max m БГ j , если max m БГ j – 0,3 ≤ m БГ j ≤ max m БГ j .

Применение процедуры вида (5) необходимо для того, чтобы обеспечить минимальный срок изготовления БГ. Статистически установлено, что варьирование массы БГ в пределах 0,3 кг практически не оказывает влияния на изменение МЦИХ КА массой свыше 2 000 кг.

Данное положение требует пересмотра при использовании методики для КА меньшей массы. Этот вопрос может быть дополнительно исследован при анализе номенклатуры изготавливаемых БГ.

Тестовая модель Так как АСБИ СА предназначена для балансировки СА ТПК «Союз МС», то для него характерно несколько расчётных случаев с различными массово-центровочными и инерционными характеристиками, представленными в таблице. Требования к массово-центровочным и инерциальным характеристикам спускаемого аппарата					Требования к обобщённой погрешности определения МЦИХ СА: по массе                            ±3 кг; по координате X                 ±3 мм; по координате Y                 ±3 мм; по координате Z                  ±3 мм; по осевым моментам инерции       ±5%; по центробежным моментам инерции                ±5%. Базовая система координат СА, относительно которой проводятся все расчёты, показана на рис. 4. В соответствии с общими формулами (1)–(3), математическая модель для задачи размещения БГ на ЛТЭ и между металлическими оболочками СА имеет следующий вид: 107 M БГ = X m БГЛТЭ + m БГ108 + j = 1 193 + Е m бгмо ; ^ min,                    (6) j = 109 где m БГЛТЭ j — масса БГ на ЛТЭ; m БГ108 — масса клея; m БГМО j — масса БГ между металлическими оболочками.
Параметры	Этапы
	Вход в атмосферу	Отстрел крышки ОСП	Посадка на ДМП
M , кг	2 880 ± 100	2 820 ± 100	2 270 ± 100
X , мм	–825 ± 5	–832 ± 5	–905 ± 15
Y , мм	85 ± 11	76 ± 8	0 ± 15
Z , мм	0 ± 7	0 ± 7	–20 ± 15
Ixx , кг·м2	1 400 ± 200	1 400 ± 200	1 200 ± 200
Iyy , кг·м2	1 680 ± 250	1 670 ± 250	1 400 ± 200
Izz , кг·м2	1 790 ± 250	1 770 ± 250	1 450 ± 200
Ixy , кг·м2	50 ± 15	50 ± 15	25 ± 15		<	0 ≤ m БГ j ≤ 8 при j = 1, 16; 0 ≤ m БГ j ≤ 1,5 при j = 17, 20;
Iyz , кг·м2	0 ± 25	0 ± 25	–30 ± 15
Ixz , кг·м2	0 ± 25	0 ± 25	40 ± 15
Примечание . ОСП — основная система парашютирования; ДМП — двигатели мягкой посадки; M — масса спускаемого аппарата (СА) с балансировочными грузами (БГ); X , Y , Z — координаты центра масс СА с БГ; Ixx , Iyy , Izz — собственные моменты инерции СА с БГ; Ixy , Iyz , Ixz — центробежные моменты инерции СА с БГ.						0 ≤ m БГ j ≤ 2,55 при j = 21, 48;         (7) 0 ≤ m БГ j ≤ 1,25 при j = 49, 107; 0 ≤ m БГ j ≤ 8 при j = 108; 0 ≤ m БГ j ≤ max m БГ j при j = 109, 193;

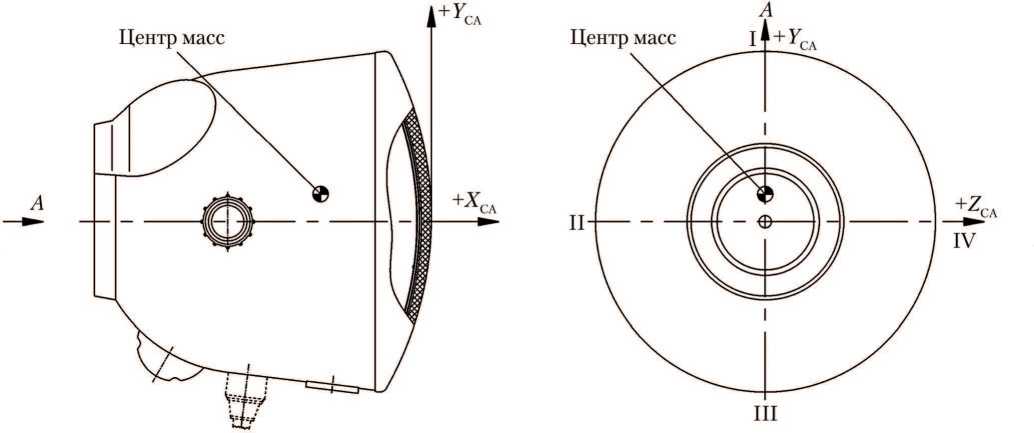
Рис. 4. Система координат и расположение базовых плоскостей спускаемого аппарата (рисунок создан автором)

min ^Г СА <

^M СА ^Г СА ⁺ 2 1 ^m БГ j ^Г БГ j

MСА + S mбг j = 1

≤ max r _СА , (8)

где M _СА — масса СА без Б Г; г СА = = [ x _СА y _СА z _СА ] ^T — вектор координат ЦМ СА; min 7 СА и max 7 СА — векторы граничных допускаемых значений координат ЦМ СА.

Из восемнадцати уравнений, получаемых по формуле (8), для первого расчётного случая необходимы ограничения по осям Y и Z , для второго — по оси X , для третьего — по всем трём осям. Сокращение ограничений вида (8) до двенадцати уравнений относительно нуля связано с тем, что, согласно документации на изделие, а также исследованиям по моделированию движения при спуске возвращаемых аппаратов [9, 10], для выполнения массово-центровочных и инерционных требований важен контроль отклонений ЦМ СА лишь по определённым осям. Стоит отметить, что на полигоне может быть принято решение о замене экипажа. На тот момент доступ к зонам размещения БГ уже заблокирован, поэтому для компенсации разницы масс основного и дублирующего экипажей за спинками изделий «Казбек-УМ» устанавливают дополнительные легковесные БГ. В таком случае они включаются в массу СА в ограничениях (8) как часть массы дублирующего экипажа и не учитываются в целевой функции (6).

Верификация модели и анализ результатов

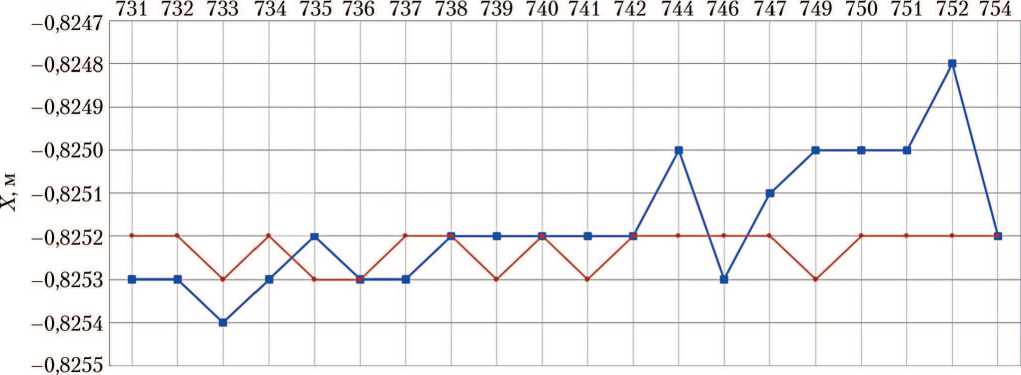
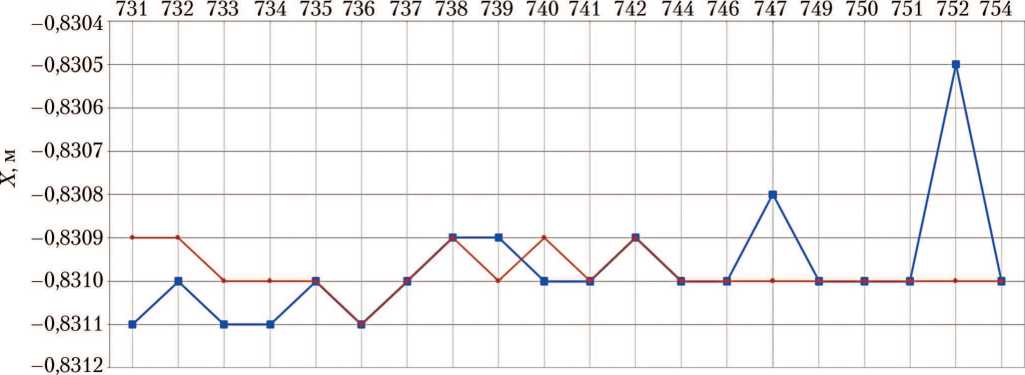
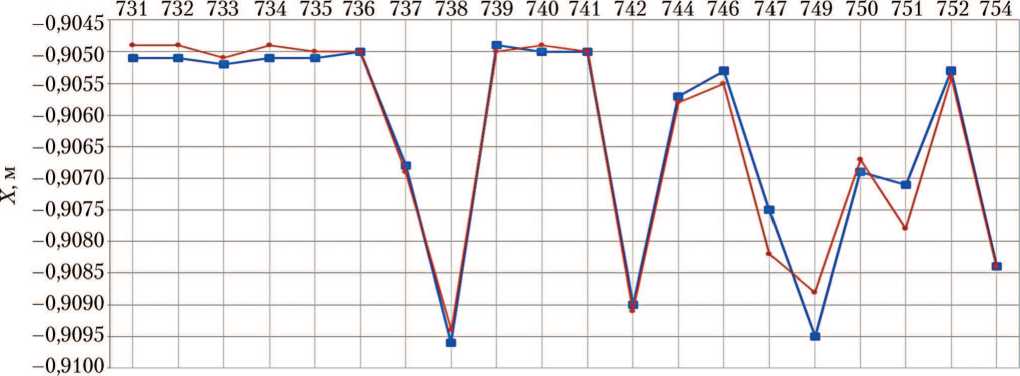
Решение целевой функции (6) найдено при граничных условиях (7), (8) симплекс-методом с учётом условий фильтрации (5). На рис. 5–7 представлены результаты для всех рассмотренных расчётных случаев. Расчёты проводились для СА № 731–754.

По графикам на рис. 5–7 можно видеть, что тестовые решения симплекс-методом новой версии АСБИ СА близки к решениям многопараметрическим методом Ньютона прежней версии АСБИ СА. Отклонения результатов от оптимальных значений в обоих случаях для всех СА не превышают погрешностей, приведённых на с. 20. Кроме того, тестовые решения более устойчивые в сравнении с прежними, судя по меньшему количеству и величине отклонений от оптимальных значений, приведённых в таблице.

Расхождения результатов по координатам ЦМ СА связаны с расхождениями по массам СА. Это объясняется тем, что при одинаковой компоновке СА в тестовом и прежнем решениях используется разное количество балансировочной массы. Такое расхождение в балансировочных массах является следствием разницы в количестве и массе БГ, размещённых на ЛТЭ и днище СА. В свою очередь, это обусловлено разными подходами метода Ньютона и симплекс-метода к поиску решения. Задачам компоновки объектов (БГ, БА, полезной нагрузки) в отсеках свойственно наличие множества допускаемых решений при заданных ограничениях. Поэтому допускаемыми считаются такие решения, которые удовлетворяют заданным требованиям.

На рис. 8 представлены результаты определения балансировочной массы для всех рассматриваемых СА. Если красная линия находится ниже синей, то расстояние между ними характеризует выигрыш в балансировочной массе, и наоборот.

Для более подробной оценки причин расхождений в моделях можно использовать метод Бруевича [2] или его модификацию, применённую в работе [11], чтобы оценить влияние различных факторов обработки данных на точность расчётов:

N БГ дм_кг

Е бг

∆ m _{БГ j} , (9)

j = 1 дт бгj где ∆mБГj — первичные погрешности масс БГ.

Функция (9) в данном случае представляет собой векторную сумму, потому что первичные погрешности являются векторами по количеству БГ для каждого СА. Здесь можно заметить, что абсолютная погрешность характеризуется ещё и передаточными отношениями масс БГ (производными), которые описывают механизм протекания процесса поиска решения задачи размещения БГ в зависимости от взаимовлияния масс.

Номер СА

а)

б)

в)

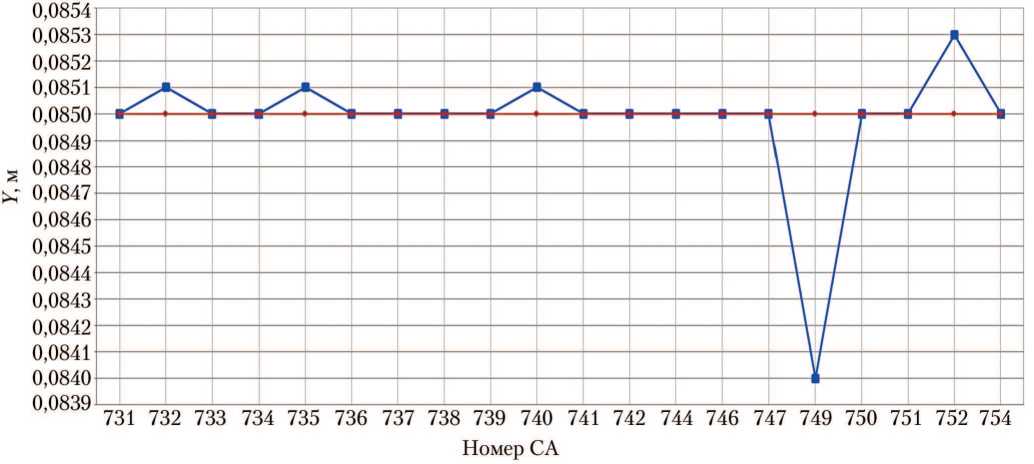
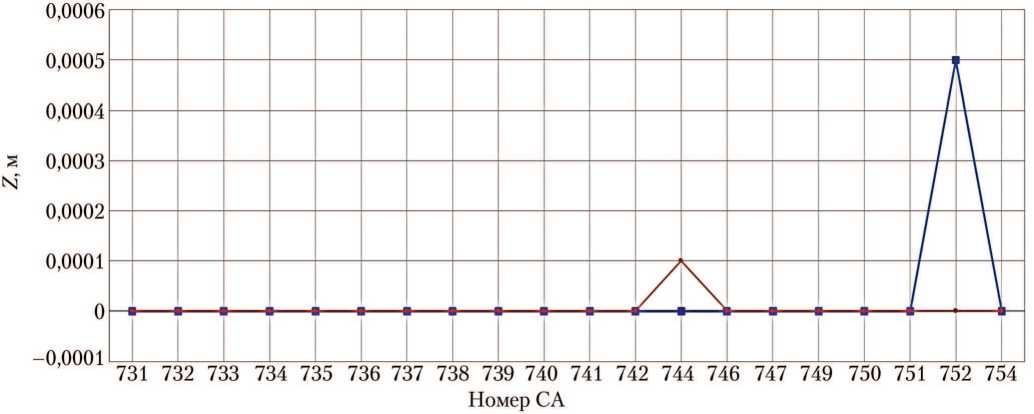
Рис. 5. Центровки спускаемых аппаратов при входе в атмосферу: а — координата по оси X; б — координата по оси Y; в — координата по оси Z; —■— — результаты исходной версии программы АСБИ СА; —•— — тестовые расчёты новой версии АСБИ на ОС Windows 2010 (рисунки созданы автором)

Номер СА

а)

б)

в)

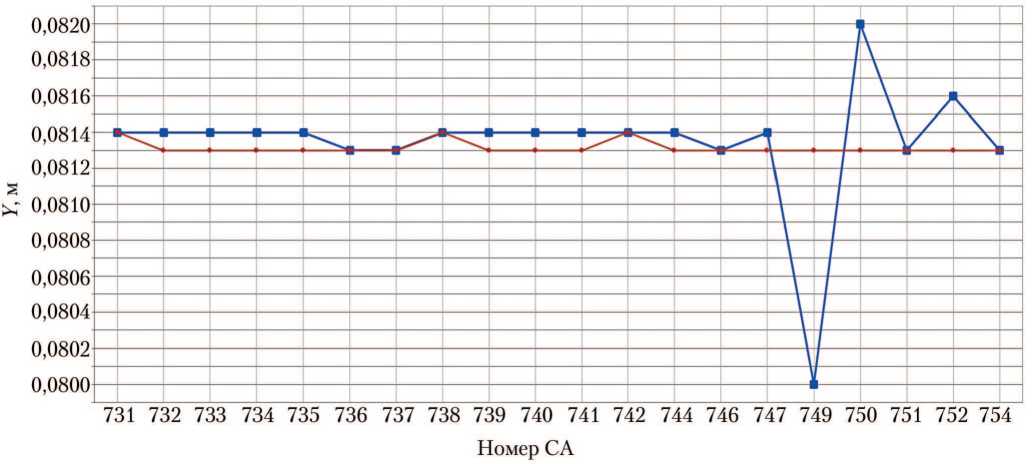
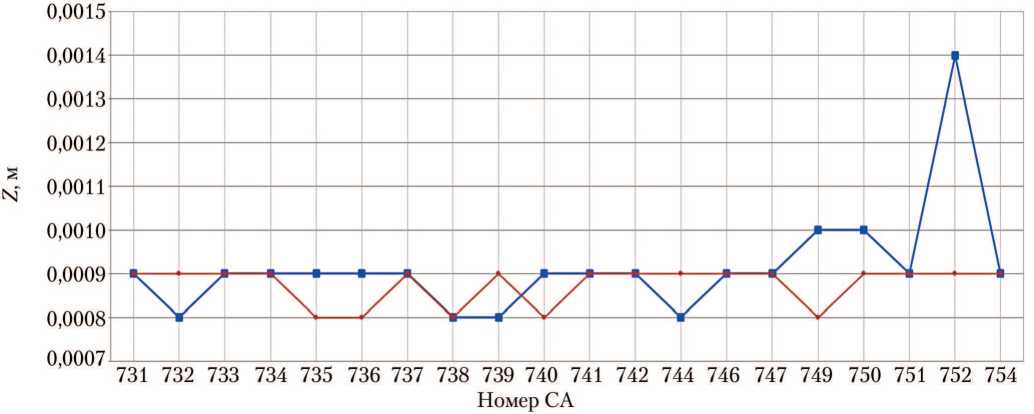
Рис. 6. Центровки спускаемых аппаратов при отстреле крышки контейнера основной системы парашютирования: а — координата по оси X; б — координата по оси Y; в — координата по оси Z; -■ результаты исходной версии программы АСБИ СА; ■*■ — тестовые расчёты новой версии АСБИ на ОС Windows 2010 (рисунки созданы автором)

Номер СА

а)

Номер СА

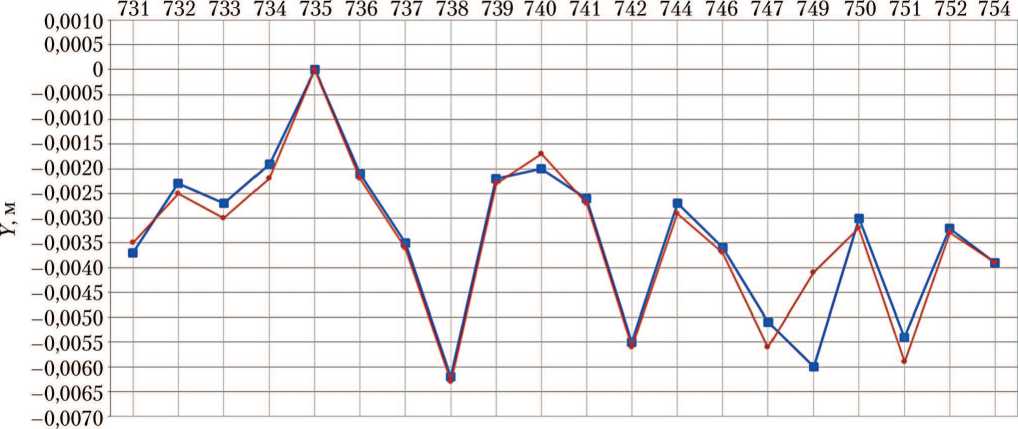
б)

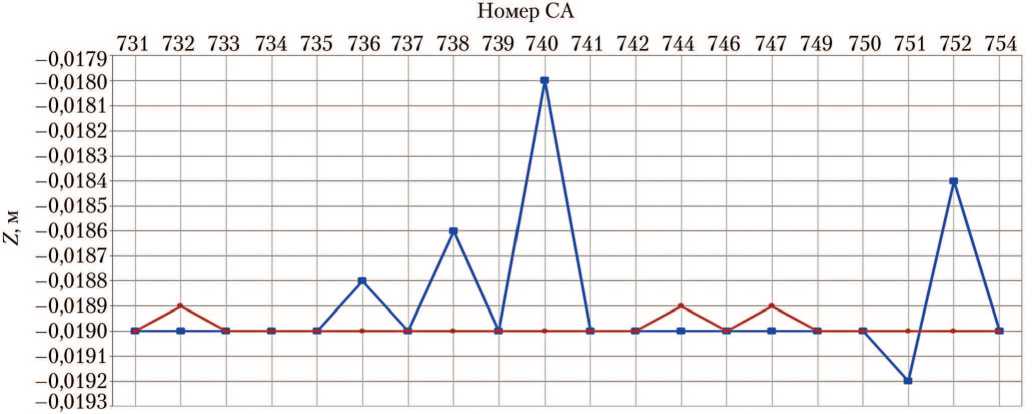
в)

Рис. 7. Центровки спускаемых аппаратов при посадке на двигателях мягкой посадки: а — координата по оси X; б — координата по оси Y; в — координата по оси Z; -■ результаты исходной версии программы АСБИ СА; -•- — тестовые расчёты новой версии АСБИ на ОС Windows 2010 (рисунки созданы автором)

На рис. 9 представлен график численного расчёта функции (9) для всех СА, использовавшихся при тестировании новой АСБИ СА на ОС Windows 2010.

Анализируя график на рис. 9, можно сделать вывод, что расхождения носят несистематический характер, так как отсутствует закономерность в изменении значений массы БГ. С целью повышения вычислительной эффективности в моделях используются барьер [система ограничений вида (2)] и фильтр [система ограничений вида (5)]. Это даёт возможность уменьшать количество итераций для поиска решения с заданной точностью.

Следует учесть, что результаты исходной версии программы АСБИ СА тоже имеют отклонения от оптимальных значений. Поэтому при переносе её на современную ОС и восстановлении математического и программного обеспечения сохраняются все прежние источники возникновения погрешностей модели (см. рис. 2):

• •    точность всех исходных данных для программы,

• •    точность обработки результатов с балансировочного стенда,

• •    точность расчёта МЦИХ СА до и после размещения БГ,

• •    точность определения масс и количества БГ (для метода Ньютона 10^–5, для симплекс-метода 10^–6).

  

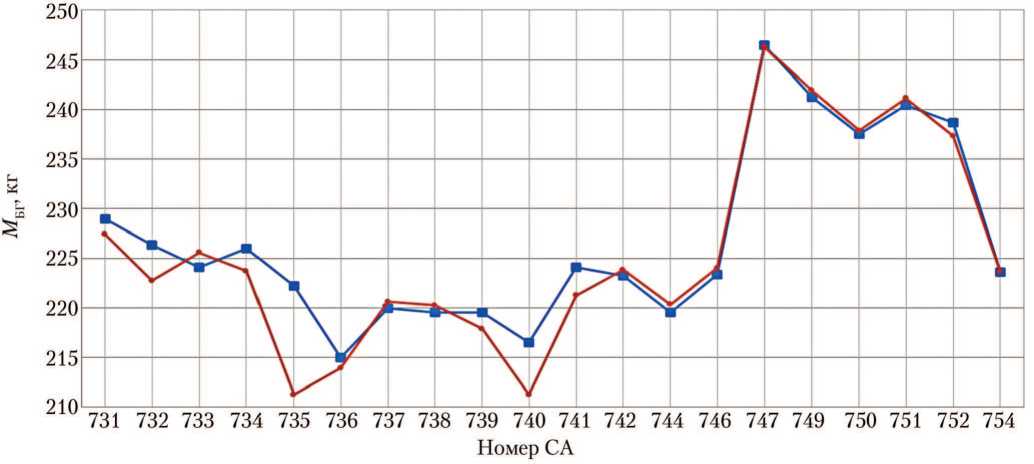
  Рис. 8. Балансировочные массы для различных спускаемых аппаратов: -■- — результаты исходной версии программы АСБИ СА; -•- — тестовые расчёты новой версии АСБИ на ОС Windows 2010 (рисунок создан автором)

  
  
  

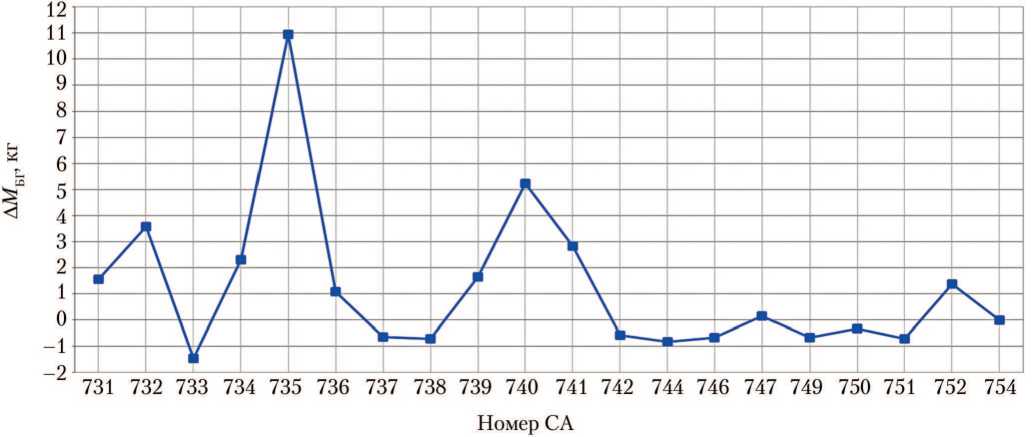
  Рис. 9. Расхождения в балансировочных массах для различных спускаемых аппаратов (рисунок создан автором)