Автомодельная редукция дифференциально-разностного уравнения для изучения его асимптотики

В моделях нового экономического роста, главным движущим фактором экономики является технологический прогресс. В концепции шумпетеровской инновационной динамики совершенствование новых технологий происходит путём их создания (инновационный процесс) и заимствования (имитационный процесс). В работе [1] приводится обзор моделей эндогенного роста, которые, в зависимости от сделанных предположений о механике процессов инновации и имитации, сводятся к исследованию различных уравнений математической физики и их дифференциально-разностных аналогов. В этих моделях конъюнктурную неоднородность описывают эволюцией распределения фирм-производителей по уровням технологической эффективности. В качестве ранжируемого по уровням показателя эффективности может браться, например, общая факторная производительность фирм, их рентабельность, капиталовооружённость и т. д. Мы будем рассматривать эволюцию, описываемую дифференциально-разностным аналогом уравнения Кортевега-де Фриза-Бюргерса, в постановке [2], которая является модификацией модели, впервые предложенной В.М. Полтеровичем и Г. М. Хенкиным в работе [3].

«Московский физико-технический институт (национальный исследовательский университет)», 2020

Пусть F_n(t^ — доля фирм, находящихся на уровне не выше п в момент времени t. Не будем конкретизировать, как именно технологические уровни различаются. Предполагается, что фирма может переходить только на более высокий уровень технологической эффективности. Убывание Ғ_п(^ происходит за счёт перехода фирм с п-го уровня (их доля равна F n (t — Ғ_п-і(^ на (п + 1)-й. Скорость убывания складывается из интенсивности инновационного процесса а и интенсивности имитационного процесса 3 (F_n+i — F_—), которая пропорциональна доле фирм уровнем выше — в данной модели реализована возможность заимствования только у ближайших передовых фирм. Экзогенные параметры а > 0 и 3 >  0 считаются одинаковым и для каждого уровня п. Они не определяются статистически — вопрос об их идентификации стоит отдельно. Например, в [4] предложили определять коэффициенты инновации и имитации косвенно, в предположении об их пропорциональности расходам на исследования и разработки, через параметры модели распространения новых технологий. Итак, имеем следующее уравнение:

^ ^{— — (а + 3(F} - +1 ^{— F} n f) ^(F - ^{— f}t -- i ) •

Поскольку, в силу сделанных предположений, распределение со временем сдвигается по п вправо, естественно считать, что отрицательные технологические уровни отсутствуют. Граничные и монотонные начальные условия имеют вид

Fo(t) = 0, 0 k-i (0) k (0) < 1,1 k (0) — 1,k > N.        (2)

В работе [2] показано, что асимптотикой решения задачи (1), (2) при а — 0 является цепочка Ленгмюра-Вольтерра. В общей постановке вопрос об асимптотике решения этой задачи остается открытым [4].

• 2.    Автомодельная редукция

Перейдём к разностям f _n — F_n — F_n-i, обозначающим долю фирм, которые находятся ровно на уровне п, и перепишем уравнение (1) в новых обозначениях:

• -^t- — —(а + 3f-+1)f- + (а + 3fn) fn-i —(Г)

• ^{— —a(f} n ^{— f} n -1) ^{— 3 (f} n +1 ^{— f} n -1^)f n •

Начальные и краевые условия (2) перейдут в fo(t) = 0, f-(0) > 0, п — 1,...,N, f-(0) —0,n>N•(2 )

Считая, что ж G Z, мы можем переписать (Г) в эквивалентном виде:

• dfде,3) — -a^f(^,t) -f(ж — h,t)] — 3[f(ж + h,t) —f (ж — h,t)]f(ж,t), h> 0.(3)

Если ж принимает только целочисленные значения и шаг h — 1, то система (2) совпадает с (Г). Однако её целесообразно рассматривать для любых, в том числе и вещественных, значений ж. В случае, когда функция f гладкая, система (Г) достаточно близко описывается системой (2). Будем сопоставлять решение (Г), (2’) с решением дифференциального уравнения (2) с неотрицательными начальными условиями f (ж, 0) —Уо(ж).                                             (4)

Считая шаг h малым, разложим f (ж ± h,t) в окрестности точки ж до второго порядка малости:

df (ж, t)    1 ₂d2f (ж,е)

f (ж ± h,t) — f (ж, t) ± h ———+ 2 h —дж2—+ °(h )•

Автомодельная редукция Ферми-Улама дифференциально-разностного уравнения (2) даёт его непрерывный аналог:

f t + ahf x + 23hf x f = 2 ah²f_xx.

Преобразование ж = 23hy + aht приводит уравнение (5) к вязкостному уравнению Бюргерса:

a

U t + uu - = ц^у, ц 8^2 •

Начальное условие (4) перейдет в

∞

u(y, 0) = uo(y) = fo(23hy),    У uo(y)dy = M.

-∞

Для решения задачи Коши (6), (7) известен асимптотический ряд [5]. Нам будет достаточно взять только первый его член, который был найден ещё в работе [6]:

■^■уЛ) = У

ц t + 1

exp {—.. ■•!

∞

VТ   I г-32

м--+ J е 3 df е 2г — 1

2УТТТг)

Этот асимптотический член также является решением уравнения (6).

Теорема сходимости формулируется в переменных подобия s = ln (t + 1), £ = y/Vt + 1, w(^,s) = Vt + 1u(y,t), действие группы преобразований которого переводит (6) в

1 2   1                           a

(6’)

w+ ( 2W - 2^WJ = ц^, ц = 8^2 • и не изменяет момент распределения

w

∞

(£, 0)=wg(^),   У

-∞

■ыем = м.

(7’)

Теорема 1 (см. [5]). Пусть w — решение задачи Коши (6’), (7’) с ц > 0 и wo Е L1 П U” ∞ обладает моментом распределения J wo(£)d£ = M. Тогда

-∞

^w(^^,s) ^

ДЦ exp {-^2/4ц} при s ^ то

∞

Т             —22

3    + J е ^{3 d}6

^{е 2Г}-¹ ^

поточечно и о L^P(R), 1 <  р <  то.

В терминах задачи (5), (4) асимптотика решения имеет вид

f(^,t) = у

a 83²(t + 1)

( x — aht )² 1

^eXP t- 2ah 2 (t+1) j

∞

Т                    —0 2

4^2M   + J е   dC е a — 1      x — aHt h^2a(t + V)

и обладает моментом

∞

У f (xpt^dx = 23hM.

-∞

Численный эксперимент позволяет увидеть, насколько хорошо асимптотика (9) решения задачи Коши (5), (4) описывает асимптотику решения задачи (2), (4) дифференциальноразностного уравнения с теми же начальными условиями.

3. Сравнение асимптотик

Решение уравнения (6) становится одноэкстремальным по ж за конечное время, вне зависимости от вида начальных условий (7). Оказывается, то же верно и для дифференциальноразностного уравнения (2). Как видно из рис. 1, мультимодальность начальной плотности распределения у решения не сохраняется. Здесь и далее расчёты проводились для трёх наборов параметров: a = 1, /3 = 0.01, когда в уравнении преобладает линейная составляющая; a = 0.5,3 = 0.5, когда и линейная, и диффузионная составляющие существенны; a = 0.01,3 = 1, когда преобладает диффузионная составляющая (случай, близкий к [2]). Шаг Һ влияет только на скорость распростри.пения волны, его везде брали равным 0.01. В качестве начальных условий бралась функция 0.3/^(5,₁)(ж)+0.4_/Д(₁о,₂)(ж)+0.3_/Д(15,1) (ж).

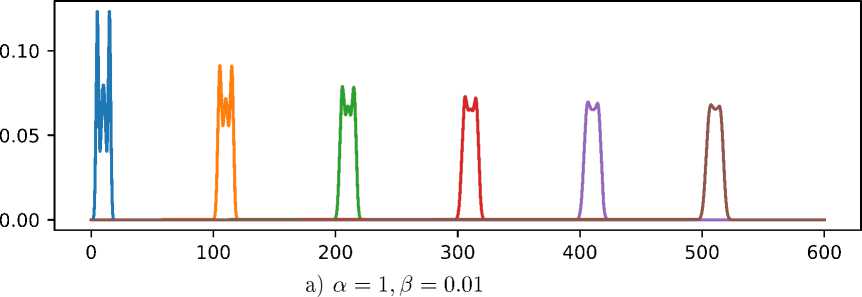
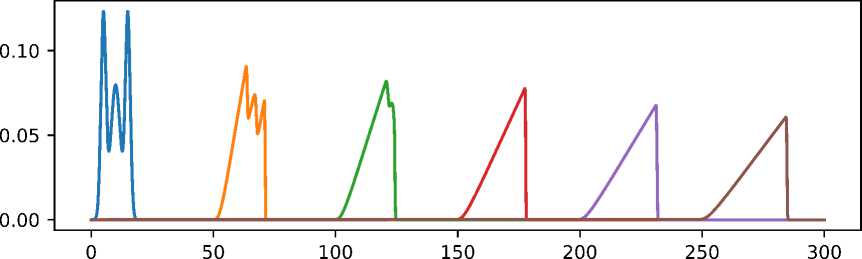
б) a = 0.5,3 = 0.5

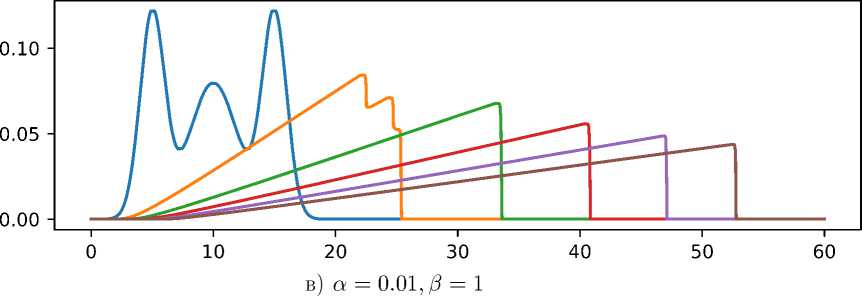
Рис. 1. /(ж, 1) по оси ж при разных параметрах а и 3 в одни и те же моменты времени

Итак, решение дифференциально-разностного уравнения (2) становится одноэкстремальным за конечное время, как и решение (6), что позволяет нам использовать их максимумы для характеристики их асимптотического поведения. Теперь в качестве начальных условий (4) для численных расчётов решения задачи Коши (2), (4) бралась плотность Я (0,1), обладающая моментом 23ҺМ = 1. Соответственно для расчёта асимптотики решения задачи (5), (4) по формуле (9) использовалось значение М = 1/23^ в зависимости от выбранных параметров а,3, ^-

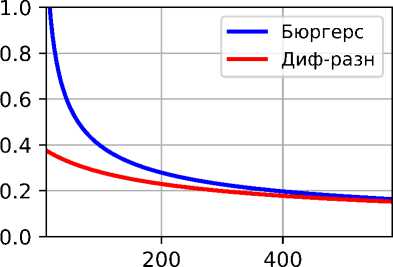
a) max / (x,t) по оси ж со временем

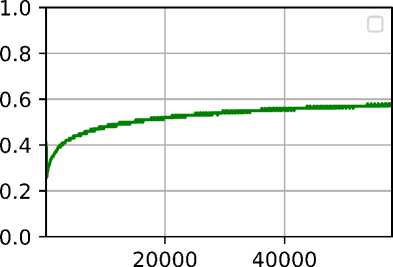
• б)    Расстояние между максимумами по оси t

  

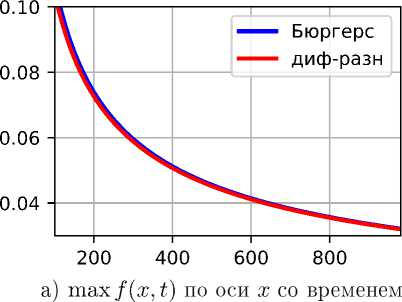
  Рис. 3. Расчёт для значений а = 0.5, 3 = 0.5, Һ = 0.01, М = 100

  
  

  Рис. 2. Расчёт для значений а = 1,3 = 0.01, Һ = 0.01, М = 5000

  
  
  

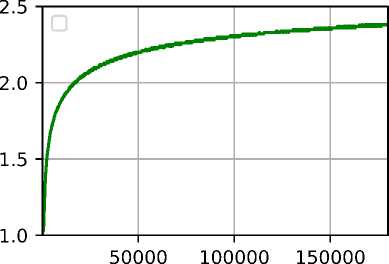
  б) Расстояние между максимумами по оси t

  
  
  

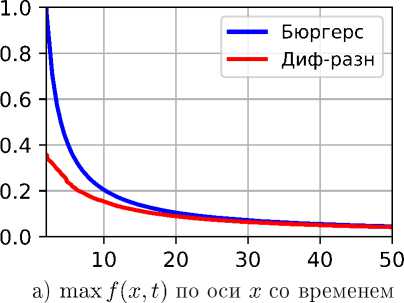
  Рис. 4. Расчёт для значений а = 0.01,3 = 1Д = 0.01, М = 50

  
  
  

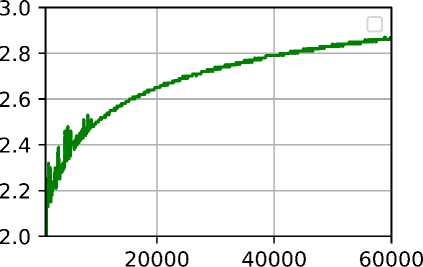
  б) Расстояние между максимумами по оси t

  
  

Как видно из графиков рис. 2—4а для всех трёх наборов параметров максимумы плотностей распределений со временем начинают совпадать. Причём, чем больше а, тем быстрее стабилизируется процесс. Графики рис. 2—46 дают представление о длительности установления фиксированной разности фаз.

Меру схожести двух асимптотик по времени можно оценить и в Li-норме как J \Jb(x, t) — fn(x,t)| dx, где Jb — асимптотика решения уравнения Бюргерса (5), fn — R решение дифференциально-разностного уравнения (2), с одинаковыми начальными условиями (4).

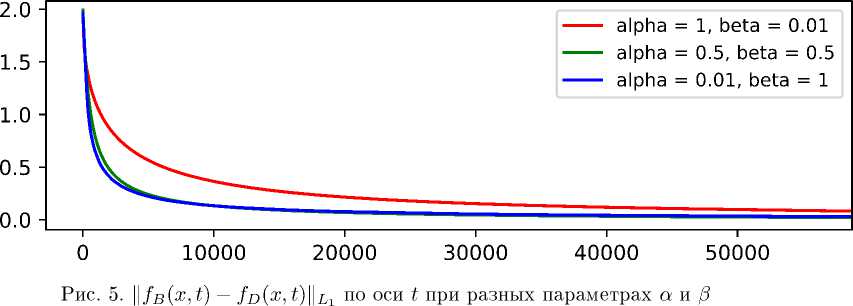
Приведённые вычисления позволяют высказать гипотезу о том, что асимптотика решения дифференциально-разностного аналога уравнения Кортевега-де Фриза-Бюргерса имеет тот же вид, что и асимптотика решения уравнения Бюргерса, к которому сводится первое после автомодельной редукции.

Работа выполнена при поддержке гранта РФФИ, проект № 17-07-00507.