Автомодельные и неавтомодельные течения вязкого газа, истекающего из вершины конуса

Научная значимость точных решений ни у кого не вызывает сомнений, а. их практическая ценность сохранилась и до нашего времени компьютерных технологий. Такого рода решения нелинейных уравнений даже в случае несжимаемой вязкой жидкости найдены для немногих задач. Особое место среди них занимает решение Джеффри—Гамеля об источнике, истекающем из линии пересечения двух плоских стенок, наклоненных друг к другу под углом. Оказывается, что исходную систему уравнений Навье—Стокса, в этом случае удается упростить и найти решение, имеющее физический смысл. Заметим, однако, что решение

Джеффри—Гамеля относится к числу наиболее нетривиальных, и его полное исследование требует значительных усилий, связанных с исследованием эллиптических функций [1,2]. Известно также, что аналогичное точное решение в осесимметричном случае найти не удается. Для течения в конусе Акербергу [3] удалось построить решение в двух асимптотических пределах: приближении Стокса (число Рейнольдса, Re ^ 0) и приближении пограничного слоя Прандтля (Re ^ то).

Что касается точных решений уравнений Навье—Стокса, описывающих течение вязкого теплопроводного газа, то они представляют собой большую редкость. В связи с этим упомянем работу [4], в которой получено точное решение для сжимаемого течения Куэтта.

Течения типа Джеффери—Гамеля для случая вязкого сжимаемого теплопроводного газа изучались ранее в работах [5-11]. В работе [5] рассмотрена возможность построения автомодельных решений типа Джеффри—Гамеля для плоского течения вязкого газа в клине. Оказалось, что в отличие от несжимаемой жидкости критерий существования автомодельного решения в этом случае не определяется соображениями размерности. В частных случаях, когда температура газа постоянна вдоль линий тока, а коэффициенты переноса являются степенными функциями температуры, для течения в клине построены аналитические решения. В [5] также установлено, что такое течение существует не всегда, а зависит от граничных условий на температуру стенок, модели газа и типа течения (сходящееся или расходящееся).

Наиболее близкими к проведенному ниже исследованию являются работы [6-8]. В [6] дано численное решение задачи об истечении газа из осесимметричного источника в канале с отводом/притоком массы и заданной температурой стенок при значении показателя степенной зависимости коэффициентов переноса от температуры к = 0.76. В работе [7] решена аналогичная задача для течения газа с граничным условием проскальзывания и температурного скачка на поверхности конуса. В недавно опубликованной работе авторов [8] рассмотрено автомодельное течение в конусе с непроницаемой границей от источника с известным расходом. В случае заданной температуры стенок были установлены критерии существования автомодельных решений и найдены критические значения определяющих параметров задачи. Для течения в тонком конусе построено аналитическое решение.

В настоящей работе на основе верифицированного численного кода решения уравнений Навье—Стокса изучаются особенности перехода неавтомодельных режимов течения Джеффри—Гамеля в автомодельные.

2.    Автомодельные течения вязкого сжимаемого газа в конусе

Следуя [8], рассмотрим радиальное течение вязкого сжимаемого газа в конусе с углом полураствора а. На рис. 1 изображена схема течения (истечение газа с расходом Q происходит из вершины конуса).

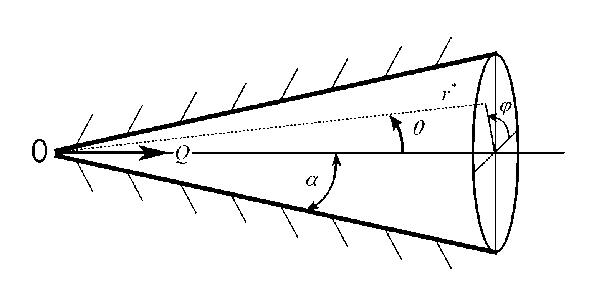
Рис. 1. Схема, течения Джеффери—Гамеля в конусе

В сферических координатах (г*, 0, у) уравнения движения имеют вид:

dr^ = 0,(D dr*

_ Эр* +   1 d(r*²CTrr ) + 1 Г 1 д ( ст гө sin Ө) _     _     1 = * * du*

dr*   r*²    dr*      r*² sin Ө дӨ       ^аӨӨ   ^^ ^{P П} dr*¹

• 1 др*      1 8(Т'*^СТгӨ) , 1 Г д^ӨӨ

• ^_ r* 8өө ⁺ Г * з   dr*   ⁺ r*   8ө~ ^{+ (}°^ӨӨ -  - ^{g Ө} = ⁰

• _р._т -u- ^ = Д а (^ 8Т* А +  1 а /* _sm өД* А ₊

• dr*    r*2 dr*        dr*     r*2 sin Ө dӨdӨ

⁺ 2р* [^CTrr ^{+ ст}2Ө ^{+ ст}2Д ^{+ 2а}2Ө ^]

Здесь использованы стандартные обозначения для термодинамических переменных ( р*, Т *, р*, S* — плотность, температура, давление и энтропия единицы массы) и коэффициентов переноса ( р* — коэффициент сд битовой вязкости, к* — коэффициент теплопроводности). Течение в конусе предполагается радиальным, так что вектор скорости V* = (u* 0, 0). Компоненты тензора напряжений ст определяются следующими соотношениями:

4р* * d   u*\

^CTrr = T ^r dr* v) , ^ст өө = " ■ ■ =

-

2р* * d U.A     _ р* du*

3     dr* r* / ^{1 СТгӨ}    r* dӨ

Перейдем теперь к безразмерным переменным р, u, Т, р, г. В качестве масштаба выберем значения р*, u0, Т* в некоторой произвольной точке р* = р* и Ө = 0, к примеру u = u*/u*. Величину r* можно условно назвать «радиусом источника». В задаче встречаются безразмерные параметры подобия: число Прандтля, отношение теплоемкостей у = с_р/с_у, число Рейнольдса Re* = p*u* г*/р*, число Маха M* = u*/ ^у RT*, а также дополнительный геометрический параметр подобия а. Здесь R - универсальная газовая постоянная, а через р* обозначено значение вязкости при Т * = Т *.

Коэффициент объемной вязкости £ будем считать равным нулю. Исследование общего случая ( = 0 не вносит ничего принципиально нового и оказывается просто более громоздким. Заметим также, что в тех случаях, когда изучается одноатомный газ, необходимость в предшествующем предположении отпадает, поскольку равенство £ = 0 является известным следствием кинетической теории [12]. Кроме того, число Прандтля Pr = с_рр*/к* в одноатомном газе близко, а для максвелловских молекул в точности равно 2/3 [12]. Поэтому далее газ будем предполагать одноатомным, подчиняющимся уравнению состояния р* = р*RT *, тогда р*/к* = 4/15R.

Коэффициенты переноса предполагаем зависящими от температуры по степенному закону р*,к* ~ Т*к. В случае более сложной зависимости коэффициентов переноса от температуры, например, при выполнении закона Сазерленда, точного решения отыскать не удается. Таким образом, автомодельное решение ищем в виде u = u(Ө) р=      р = Рт-2р(Ө) Т = ТМр= (ТМА2 р= у р рт 1 Р   рт+21 Р        Р 1       р2т р [ р2т    1 Pr(1  у )р

При подстановке соотношений (6) в уравнения (1) - (5) приходим к необходимому условию согласования:

2тк = 11

а исходные уравнения редуцируются к системе обыкновенных дифференциальных уравнений (ОДУ) [8]:

1 й (грк ^^^о , 4/ ^*         к ,   Re0 Г/ ,            21 _ п			(7)
sin Ө йӨ	йӨ     +3(m
	Reo dp = (1 -(7M*)k йӨ	m)T к ^ + 2(1+ m) 4, (uTк ), йӨ 3       йӨ	(8)

Reo (7M*)k PU (2  m l) = Pl   n[4m*T 1+k + - flafl(T к   sin Ө) I +      (9) \      7 — 1) Pr(7 — 1) [            sin Ө йӨ \ йӨ     /J + [3(m + WTк +Tк (У)* с краевыми условиями на оси, Ө = 0:

^u = р = 1, Т = р = -1-2

(Ю)

(И)

7м*

и на поверхности конуса, Ө = а:

u = 0, Т = T_w .

Краевая задача (7) - (11) была исследована численно в работе [8] для случая течения газа твердых сфер (см., например, [12,13]), т.е. при к = 1/2, m = 1. Там же было найдено, что автомоделвное решение не существует при произвольной комбинации определяющих параметров ( а, Reo, Mo, T_w, Q\ а только при задании каких-либо двух. Кроме того обнаружено, что для рассматриваемого течения имеет место ограничение на величину угла полураствора конуса а и значение числа Маха Mo. Установлено, что при угле а > а* ~ 0.9 (~ 52 град) нарушается условие сплошности среды, а максимальное число Маха M_max ~ 2.2 достигается на оси конуса при а ^ 0.

3.    Прямое численное моделирование течения вязкого газа в конусе

Для численного моделирования течения Джеффри—Гамеля рассматривается ламинарное течение вязкого теплопроводного совершенного газа в расширяющемся усеченном конусе. Схема данного течения представлена на рис. 2.

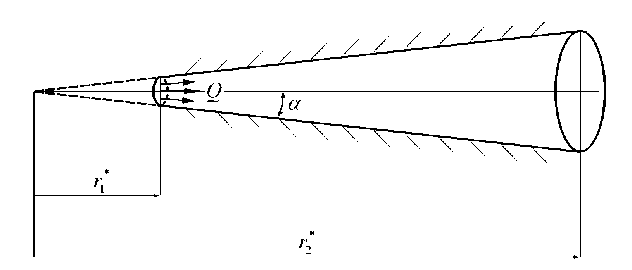
Рис. 2. Схема, течения в усеченном конусе

Здесь г* — расстояние от вершины конуса до входного сечения канала, г* — длина конуса. от вершины до выходного сечения. Расчеты при различных значениях определяющих параметров задачи проведены с помощью численного решения уравнений Навье—Стокса, в двумерной осесимметричной постановке для трех различных конусов, геометрические параметры которых приведены в таблице.

№	a (рад)	т* (м)	т2 (м)
1	0.01	0.1	0.8
2	0.05	0.05	0.4
3	0.1	0.05	0.4

Рассматривается течение одноатомного газа — гелия с коэффициентами переноса, зависящими степенным образом от температуры по закону (T*)1/2. В соответствии с соотношениями (6) для газа твердых сфер основные газодинамические параметры в автомоделвном течении должны изменяться по закону

* п

- _т ,t * - _т12, р*

∼

1     .*

—т , Р т*3

∼

т* 1

а числа M и Re должны сохраняться на линиях Ө = const [8].

Ниже точность выполнения этих законов на автомодельных режимах течения и степень отклонения от них на неавтомодельных режимах проверяется численно. Заметим, что данная процедура является одновременно и верификацией численных расчетов, поскольку результаты расчетов на автомодельных режимах сравниваются с точными автомодельными решениями.

Как уже отмечалось, автомодельные решения существуют только при определенной комбинации определяющих параметров (a, Reo, Mo, T_w , Q), которая найдена в [8] в результате анализа краевой задачи (7) - (11). К примеру, установлено, что для каждого угла a полураствора конуса достаточно задать безразмерный расход Q, а чпела Mo и Reo при этом определяются единственным образом.

3.1.    Результаты численных расчетов автомодельных режимов течения

Для реализации автомодельного течения в усеченном конусе необходимо задать специальный (автомодельный) закон распределения температуры на стенке — T* = (T* МЛ/т*)², а также особым образом подобрать параметры течения во входном при т* = т* и выходном сечениях канала, т* = т*. На входе задаются: скорость п*, плотность р* и размерный расход Qo, а на выходе: давление р2 и температура T* (см. рис. 2).

Вначале рассмотрим течение в канале с углом полураствора a = 0.01. Параметры потока на входной и выходной границах: расход газа: Qo = 6.25 • 10^-6 к г/с, п* = 308 м/с, р* = 8.75 • 10^-3 к г/м³ и р* =4 П a, T* = 4 К. Столь малые значения давления и температуры на правой границе обусловлены быстрым законом убывания газодинамических параметров (12).

Расчеты показывают, что в рассматриваемом случае величина Mo на оси резко возрастает от значения Mo ~ 0.4 в начальном сечении до Mo = 1 в сечении т* = т* + А, и далее выходит на константу в области длиной А_авт ~ 0.54 м; за этой областью, Mo снова слегка возрастает, что обусловлено концевыми эффектами на границе расчетной области (см. рис. 3).

Заметим, что течение в области постоянного Mo соответствует автомодельному режиму, на который решение выходит довольно быстро. Число Reo в области автомодельности — Reo ~ 13500 примерно на 5% отличается от соответствующего точного «автомодельного» значения, полученного в [8]. Распределения скорости, плотности, давления и температуры на оси конуса в логарифмических координатах представлены на рис. 4.

На представленных на рис. 4 кривых наблюдается прямолинейный участок, начинающийся от значения 1д(т*/т*) ~ 0.2. Этот участок функционально можно представить в виде lg(/*/Л**) = const - ™ 1д(т*/т*), где /* = {'*, Т*, Р*, Р*}- С помощью полученных зависимостей можно определить показатель степенной зависимости п для основных газодинамических параметров. Так для скорости как функции т* на участке Аавт получаем п = 0.96; аналогичный показатель степенной зависимости m в автомодельном точном решении: m = 1; для температуры соответственно имеем п = 1.94 и 2m = 2; для давления — п = 2.98 и 2 + m = 3, а для плотности — п = 1.06 и 2 — m = 1. Это означает, что, начиная с некоторого значения А + т* = 100.2 ~ 0.16м, зависимость газодинамических параметров от расстояния т* с точностью до 6% соответствует автомодельному режиму (12).

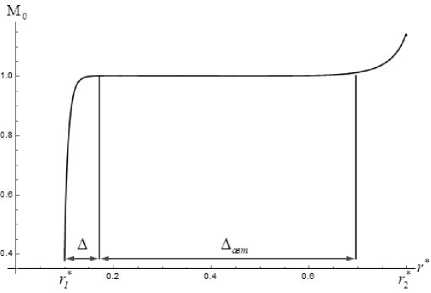
Рис. 3. Зависимость числа Маха на оси конуса а = 0.01 от расетояиия т*

Аналогичные расчеты проведены для конусов с углами полураствора а = 0.05 и 0.1. При а = 0.05 автомодельные законы (12) выполнены с точностью до 6%, а при а = 0.1 — до 7%. Как видно из приведенных выше результатов, автомодельный характер течения реализуется в некоторой внутренней области канала, в которой при заданном расходе и угле полураствора конуса, числа Маха и Рейнольдса, оказываются близкими к найденным в точном решении [8].

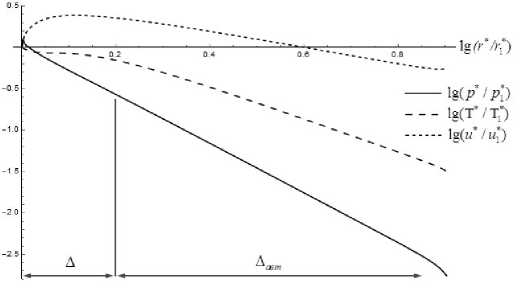
Рис. 4. Зависимость газодинамических параметров на оси конуса а = 0.01 от расетояиия т*

Интересно изучить вопрос, связанный с возможностью образования местных сверхзвуковых зон. Естественно предположить, что для заданного а при величине расхода Qo, большем некоторого критического значения, в окрестности оси конуса должна возникнуть сверхзвуковая область. Действительно, расчеты показывают, что в конусе с углом полура-свора а = 0.1 при Qo ~ 3.98 • 10^-6 к г/с возникает сверхзвуковая зона (см. рис. 5).

Видно, что в центре канала образуется коническая область с углом полураствора 3 < а, в которой Mo > 1. Результаты систематических расчетов показывают, что при различных значениях а и фиксировайном числе Mo, отношение 3/а остается примерно постоянным. Для конусов с углами а = 0.01, 0.05, 0.1 и 0.2 при Mo = 1.1 это отношение приблизительно равно 0.32, а при Mo = 1.2 отношение 3/а ~ 0.44.

Рис. 5. Поле чисел M0 для конуса a = 0.1

3.2.    Результаты численных расчетов неавтомодельных режимов течения

Рассмотрим теперь неавтомодельные режимы течения. Для этого во входном сечении зададим граничные условия, соответствующие автомодельному режиму, а в выходном сечении — отличающееся от автомодельного. В качестве примера рассмотрим течение в конусе с углом полураствора a = 0.01.

Во входном сечении профили скорости и температуры записываются в автомодельном виде: -1 = u*ax^{(1 -}(У/а)²), Т* = ^Т* ax^-(Ө/а^)2(Т*ax^- Т* ) [8], где Ө - угол между осью конуса и лучом, проведенным из вершины (см. рис. 1). В расчетах для -*_ax, Т*_ax и 7^ приняты следующие значения: -*_ax = 2631 м/с, Т*_ax = 2000 К и Д* = 1400 К. На правой границе расчетной области: Т2* = (Т*_ax — (Ө/а)²(Т*_ax — Т))(г*/г*). Давление, в зависимости от режима, варьировалось от значения р2 = 0.21 Па, соответствующего автомодельному режиму течения, до значений, отличных от автомодельного: р2 = 2, 5 и 20 Па. Зависимость числа Маха на оси конуса для разных режимов представлена на рис. 6.

— Автомодельный режим

• -    Неавтомодельный режим, р,=2Па

• ■    - Неавтомодельный режим, р_г =5Па

• -    Неавтомодельный режим, р^ = 20 Па

Рис. 6. Распределение числа M0 для ко нуса с a = 0.1 при различных режимах течения

На рис. 7 построено распределение давления на оси в автомодельном и неавтомодельном режимах. Видно, что до некоторой точки г *_вт давление р* ведет себя согласно (12) и далее выходит на константу, совпадающую с давлением в выходном сечении. Отсюда можно сделать вывод, что размер автомодельной области определяется отношением давлений во входном и выходном сечении. Это отношение можно приближенно аппроксимировать следующей зависимостью:

Г*в т = Г* (р1 /Р2 )1/3.

Заметим, что в том случае, когда р2 близ ко к р1, значение давления остается практически постоянным по всей длине канала; остальные газодинамические параметры, измеренные на оси, убывают по степенному закону, но с другими показателями степенной зависимости.

— — Автомодельный режим

-----Неавтомодельный режим, р2=5Па

...... Н еавтомодельный режим, р2 = ^0 Па

----Неавтомодельный режим, р₂ я й

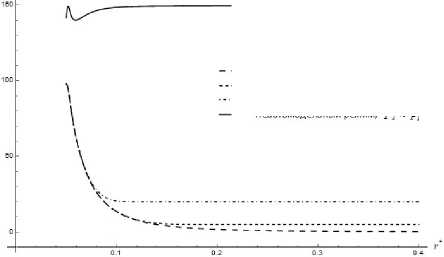
Рис. 7. Распределение р* для ко нуса с а = 0.1 в различных режимах течения

4.    Заключение

Проведен численный анализ задачи о стационарном течении вязкого сжимаемого теплопроводного газа, твердых сфер в расширяющемся канале с заданной температурой стенок. Рассмотрены как автомодельные, так и неавтомодельные режимы течения. С помощью численного моделирования уравнений Навье-Стокса установлено, что автомодельные режимы течения действительно реализуются при задании определяющих параметров в форме комбинаций, найденных ранее в результате точного автомодельного решения задачи [8].

Обнаружены решения, соответствующие смешанному характеру течения в конусе, когда, в окрестности оси возникает местная сверхзвуковая зона. Отметим, что относительный размер этой зоны практически не зависит от угла а, а зависит только от величины числа Мо на оси конуса.

Численное исследование неавтомодельных режимов течения в том случае, когда, граничные условия отличаются от автомодельных, показало, что и в этом случае в решении наблюдается некоторая область автомодельности. Размер этой области примерно пропорционален кубическому корню из отношения давлений на левой и правой границах расчетной области.