Автомодельные течения газа Абеля - Нобля в плоском диффузоре

Рассматривается течение типа. Джеффри - Гамеля вязкого газа. Абеля - Нобля в плоском клиновидном канале. Классическое решение Джеффри - Гамеля описывает плоское течение несжимаемой вязкой жидкости в пространстве между двумя стенками, наклоненными под некоторым углом друг к другу [1]. Это одно из немногих известных точных решений уравнений Навье - Стокса, выражающееся через эллиптические функции.

Автомодельные течения вязкого совершенного газа, в плоских и осесимметричных каналах впервые были изучены в работах [2-7]. Точное аналитическое решение задачи о ламинарном течении газа, от источника, массы в клине получено в работе [8], а. в [9] приведено аналогичное точное решение для плоской струи вязкого газа, от линейного источника, импульса. Более общее решение для случая течения совершенного газа, при произвольной зависимости коэффициентов вязкости и теплопроводности от температуры дано в работе [10], а. в [11] рассмотрены несимметричные режимы течения.

Задача Джеффери - Гамеля в несжимаемой жидкости при фиксированном расходе изучалась в работе [12], в которой определены точки бифуркации и области существования течений в плоском диффузоре. Заметим, что исследование в рамках уравнений Навье -Стокса, отдельных иных задач также сводится к решению Джеффери - Гамеля. Например,

в работе [13] показано, что на большом удалении от твердой границы ламинарное течение, индуцированное пространственной пристеночной струей, соответствует течению типа Джеффери - Гамеля около развернутого угла. Турбулентным автомодельным течениям типа Джеффри - Гамеля в рамках классической модели Прандтля посвящена недавняя работа [14].

Во всех упомянутых выше работах газ предполагался совершенным, подчиняющимся стандартному уравнению состояния. В настоящей статье изучается возможность построения автомодельных решений для газа, который подчиняется более общему уравнению состояния Абеля - Нобля [15].

Функциональная зависимость между плотностью р, давлением р и температурой Т является экспериментально установленным фактом, который подтверждается кинетической теорией газов. В газодинамике при обычных условиях, как привило, используется уравнение состояния совершенного газа, которое имеет вид р = рКТ, где R — газовая постоянная. Более общая форма уравнения состояния газов при достаточно высокой температуре и низком давлении может быть записана в виде вириального уравнения состояния [16]:

= 1 + В(Т )р + С ( т )р² +..., pR!

где В(Т ), С(Т ) и т.д. — функции только температуры и не зависят от давления и плотности. Первое приближение, В(Т ) = С(Т ) и т.д.= 0, соответствует стандартному уравнению состояния совершенного газа. Если во втором приближении функцию представить в виде

В(Т ) = b —

bi

RТ,

а С(Т ) и другие члены положить равными нулю, то получим известное уравнение состояния Ван-дер-Ваальса:

р + bip2 = pRТ (1 + bp), описывающее свойства жидкости как в газообразной, так и в жидкой фазах. При bi = 0 и малых значениях параметра b > 0 приходим к уравнению состояния газа Абеля — Нобля, которое с удовлетворительной точностью применимо к течениям газа при давлениях от 50 до 2000 МПа. В практических приложениях модель газа Абеля — Нобля используется во внутренней баллистике оружейных каналов, а также при расчете течения газа в различных ракетных установках [15].

2.    Основные термодинамические соотношения для газа Абеля — Нобля

Будем считать, что газ подчиняется уравнению состояния Абеля — Нобля:

р(1 - bp) = pRТ, где постоянные Rub для простоты записи отнесены к молярной массе р. Вводя обозначение для «эффективной плотности» R = р/(1 — bp), имеем р = RRТ.

Заметим, что при b >  0 эффективна я плотность R всегда больше p. Внутренняя энергия такого газа совпадает с внутренней энергией совершенного газа е = с ^ Т, а энтальпия Һ находится по формуле

Һ = е + р/р = е + р(Ь + ^-) = е + RT + Ьр.

р

Откуда заключаем, что удельная теплоемкость при постоянном давлении ср совпадает с удельной теплоемкостью совершенного газа:

дҺ

Ср =      р =с+ R’ а формула для энтальпии принимает вид

Һ = с_рТ + Ьр.

Найдем выражение для скорости звука a = у/ (др/др) _s в газе Абе ля-Нобля; s — энтропия. Нам это потребуется в дальнейшем для нахождения числа Маха. Запишем полный дифференциал энергии в следующей форме:

de = Tds - pdV = Tds + 4 dp.

Р2

Выберем в качестве независимых переменных р и р, тогда выражение для de можно представить в виде de =

(др), ^{dp +} (др) р ^dp■

Приравнивая правые части (1) и (2), находим выражение для dp:

₌    ^Tds     р/р^{2 - (де/}др') р

р   (де/др)р +    (де/др)р

Предполагая, что давление является функцией энтропии и плотности, р = p(s,p), имеем dp = (4 р ds+(4, dp■

Сравнивая формулы (3) и (4), получаем

( др \ = р/р2 - (де/др)р др ,       (де/др)р’ откуда окончательно находим выражение для квадрата скорости звука:

s

- In ^, R A

^с р Т = —

Су

При условии, что энтропия постоянна, р/R?1 = const, вновь находим квадрат скорости звука:

a = (др), - теR T р^_р + 1А.)

= И 7 = (И )2TRT

Откуда a/a = R/р, г де a — скорость звука в совершенном газе. Из полученной формулы следует, что при одинаковой температуре скорость звука в газе Абеля — Нобля больше скорости звука в совершенном газе.

3.    Вывод определяющих уравнений автомодельного течения

Рассмотрим течение вязкого газа Абеля — Нобля в плоском клиновидном диффузоре (рис. 1).

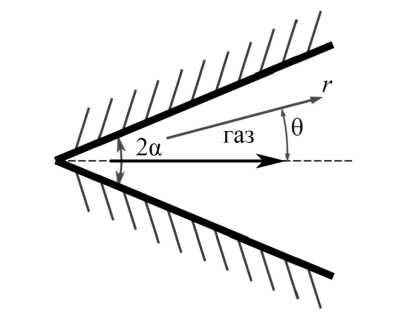
Рис. 1. Схема течения газа в клине

Течение описывается уравнениями Навье — Стокса, которые в цилиндрических координатах имеют вид дһ    Эр 1

Р дг    дг т

1Э / ЭТ\ ГэГ у™!*

1 д ( дТ

+ Г2 ЭӨ V90 ) +

+²р [(^Err)2 + (E gg ⁾² + ²⁽6_r g )²] ^-

2ц /1 д (ru) \ ² 3 r дг )

•

д ЭГ (гРи) = 0,	(6)
ри? = -ЭР + 1 [? (rarr) + Ә4i g -a gg 1 , дг     дг r дг         ЭӨ	(7)
0 = -1 э р + £ д ( 2  1 + 1 дa gg г ЭӨ г2 дг     rg' r ЭӨ ’	(8)

Здесь для термодинамических переменных использованы стандартные обозначения, а символами ц и к обозначены коэффициенты сдвиговой вязкости и теплопроводности соответственно.

Течение в клине предполагается радиальным, так что вектор скорости V = (и(г , Ө), 0). Компоненты тензора напряжений а определяются следующими выражениями:

• a„- = 2це„. - 2^^- (ги) ;   a gg = 2pE gg - 2^ (ги) ;   a_r g = a gr = 2pE_r g ,

3r Эг                      3r Эг ди        и         1 ди

Err =    ; Egg = _; Erg = у зу • дг         r         2r ЭӨ

В качестве характерных масштабов газодинамических параметров выберем значения ро, ио, ТО в некоторой произвольной точке r = Го на оси клина Ө = 0 и перейдем к безразмерным переменным:

- Р - ^и         Р ^т Т _ р _ и

Р = —, и = —, Р = --о, Т = —, ц = —, к = —•

Ро        ио         Рои2         То        цо        ко

В уравнение энергии (9) , записанное в этих переменных, входит число Маха, которое с учетом (5), в отличие от работ, где рассматривалось течение совершенного газа, вычисляется по формуле

M0 = "  = (1 - Р0Ь)2-Ң- = (1 - роф²М2.

^0                   'T'-f^G

Здесь M q = u_q/q_q ^- число Маха в совершенном газе. Тогда уравнения (6) — (9) в безразмерных переменных, помеченных черточкой сверху, принимают следующий вид:

(три) = 0, дт

(Ю)

(П)

__Эи Эр     1   Г д__ д<_тӨ puд_ = -дт + TRQ [д?_)+ "әө" - _өө

0 = -1 др .    1   д ,_2_  х  +   1  д_өө т дӨ   _2Reo д_   СТгӨ    _Reo дӨ 1

__ д ( Т ,   \   _др рн-лт              ' 5Р0 р = н+ дт Ы2 (т -1)      ) дт

1         1 д (__дТ 1 д д_ӘТ

⁺М2(т - 1)Re_oPro № V ^кд^ ⁺ Т² әө (^кдӨ  ⁺

⁺RP [(з,Д + («⁾²     ө⁾²]- ^R q (Т)².

Уравнение состояния в этом случае записывается в форме TM2р(1 - Ьрор) = рТ, где Reo = ропого/ро — число Рейнольдса; Pro решения уравнений (10) — (13), как и ранее сфер [8], будем искать в виде

= Ро c_p/k q — число Прандтля. Автомодельные

для модели совершенного газа сверхтвердых

-    ^н(Ө)     -     7 АХ    -   Р^(Ө)

^{u ;} Р = Р^(Ө);    р ₂ ^;

т

Т (Ө).

¹       т2 ^;

р = const; к = const.

Легко видеть, что уравнение неразрывности в этом случае выполняется автоматически. При иной зависимости коэффициентов переноса р и к от температуры (модель газа твердых сфер, максвелловского газа или газа, подчиняющегося закону Сазерленда) автомодельные решения для газа Абеля — Нобля найти не удается. После подстановки (14) в (10) — (13) получим следующую систему обыкновенных дифференциальных уравнений, где штрихами обозначены производные по Ө:

2р + ри2 +    = 0,

Re0

о= -р' л² -

Re0

-2рн

Т

(T - 1)!П2

+ Ьр_ор

-2ир +

4Т + Т''        4u ² + (u ' ) ²

]М2 (т - 1)Re0Pr      Reo

Уравнение состояния для переменных р(Ө), Т (Ө) и р(Ө) имеет вид

7мор(Ө)(1 - 5рор(Ө))= р(Ө)Т(Ө).

С учетом уравнения состояния, уравнение энергии упрощается. Тогда полученную систему дифференциальных уравнений можно переписать в более компактной форме:

2р + рП2

п’’

+     = О,

Reo

0 = -р + ІТ" -

Reo

1 — bop

0 = 2 пр---— + у — 1

4Т + Т ‘‘

ТдЗ ЛГУТ+

Mo (у - 1)ReoPr

4п2 + (п‘)2 Reo

с граничными условиями прилипания и заданной температуры на стенке:

п(±а) = 0, Т (±а) = Тш и условиями нормировки на оси клина:

п(0) = 1, Т(0) = 1, р(0)= ^2 1     , где введено обозначение bo = bpo.

Будем искать симметричные решения системы уравнений (15) — (17), такие, что для всех газодинамических переменных будет выполняться условие d/dӨ = 0 пр и Ө = 0. Проинтегрируем уравнение (17) с учетом граничных условий и условий нормировки. В результате получаем

2(п — 1) +         1

Re0     уМ 2(1 — bo) ’

Откуда видно, что при больших числах Reo и умеренных значениях Mo давление оказывается практически постоянным по всей ширине канала.

• 4.    Течение в тонком клиновидном диффузоре

Рассмотрим частный случай дозвукового, Mo ^ 1, течения газа Абеля — Нобля в тонком клине, а ^ 1. Будем предполагать, что для основных параметров течения выполняются следующие оценки:

уМ2(1 — bo)

a2Reo ^ 1’

В этом случае давление можно считать постоянным во всем поле течения:

1 р = —------ = const.

Введем новое обозначение для независимой переменной, Ө = Ө/a. С учетом условий симметрии из уравнения (15) в нулевом приближении находим a2Reo        -2

уМ o(1 — bo)         ’

Из условия нормировки определяем необходимое условие автомодельного течения:

a2 Reo уМ o(1 — bo)

Решая уравнение энергии, с учетом условия (18), для скорости и температуры в нулевом приближении окончательно получаем и = 1 - Ө2, Т = 1.

Как и для течения совершенного газа в узком клине, полученное решение по форме оказывается совпадающим с известным решением Пуазейля [10]. Заметим, что в нулевом приближении полученный резулвтат отличается от соответствующего решения для совершенного газа толвко значением критических параметров, связанных соотношением (18).

5.    Численное решение задачи автомодельного течения газаАбеля — Нобля в клиновидном диффузоре

Для нахождения численного решения удобно переписать систему (15) — (17) относительно плотности р;

2рТ

₇М2(1 - bop)

+ Рп2 +    = 0,

Reo

рТ = 2(и - 1) +        1

7M2(1 - bop)     ^Re0     7M2(1 - bo)

2 рТи         4Т + Т"      4и² + (и’)²

7M0(7 - 1)   M0(7 - 1)ReoPr      Reo

Полученную систему ОДУ можно решать как задачу Коши с начальными условиями [11]:

и(0) = 1, Т (0) = 1, р(0) = 1

и условиями симметрии:

du dd

= 0, 9=0

dТ dd

= 0.

9=0

Для этого вначале задаются некоторые значения параметров подобия Reo и Mo. Затем численное интегрирование продолжается до тех пор, пока скорость на стенке и(Ө_п) не обратится в ноль. Отсюда находится полуугол раствора клина а = Ө_п и температура на стенке: Т_№ = Т (ӨД.

При проведении расчетов с использованием неявного метода Эйлера и метода Рунге — Кутты для решения системы (19) — (21) существенной разницы в результатах не выявлено. В практических расчетах удобнее задавать число Маха Mo, рассчитанное по формуле для совершенного газа. Значение числа Маха Mo в газе Абеля - Нобля связанно с Mo простым соотношением:

Mo = (1 - bo)Mo.

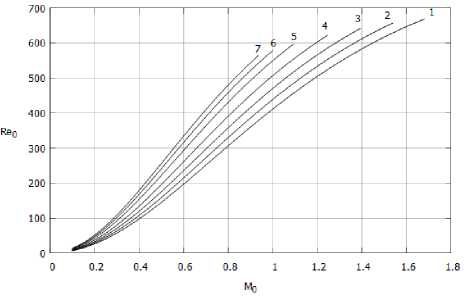
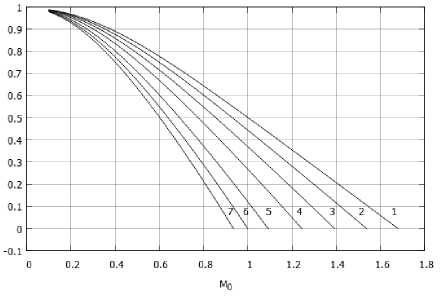
Зависимости Reo (Mo) и Т_ш (Mo) для течения одноатомного газа в клине с полууглом раствора а = 0.0 рад при различных значениях параметра bo приведены на рис. 2а, 26. Из рис. 26 видно, что при некотором критическом значении M* температура на стенке обращается в ноль, и автомодельное решение перестает существовать [10,11,14].

Как отмечалось ранее, уравнение состояния газа Абеля — Нобля справедливо при небольших значениях bo- При bo ^ 1 происходит фазовый переход в иное агрегатное состояние. Напомним, что значение bo = 0 соответствует течению совершенного газа. Отметим также, что при увеличении параметра bo скорость звука возрастает и при значении bo ~ 0.4592 сверхзвуковое течение газа Абеля - Нобля в клине становится невозможным, что хорошо видно на кривой зависимости максимально возможного M* от bo (рис. 3).

а)

Рис. 2. Зависимость числа, а) Рейнольдса, б) температуры на стейке от числа. Маха, на оси клипа. a = 0.05 рад

1. Ь о = 0.0; 2. Ь о = 0.1; 3. Ь о = 0.2; 4. Ь о = 0.3; 5. Ь о = 0.4; 6. Ь о = 0.4592; 7. Ь о = 0.5

б)

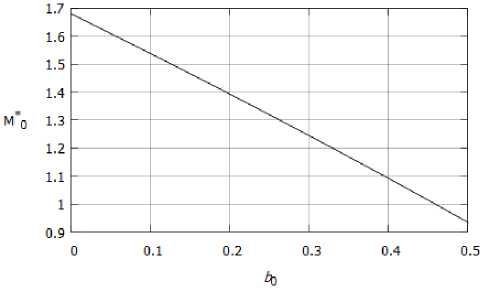
Рис. 3. Зависимость максимально возможного числа Маха от параметра Ьо в клине a = 0.05 рад

Проведем сравнение основных параметров течения газа. Абеля — Нобля и совершенного газа. Для этого рассмотрим течение нитроглицерина [15] в узком клине a = 0.02 рад при следующих условиях: ро = 150 к г/м 3, ро = 215.1 МПа, Ь = 0.001413 м³/кг (Ьо = 0.21195), 7 = 1.18. Расход газа в клине находим по формуле

/ а                   га

р(Ө)и(Ө) ДӨ = 7оReo / р(Ө')п(Ө') ДӨ = poReoQo,

- а                         J —а где Qo — безразмерное значение расхода. Как было установлено выше, в автомодельных течениях коэффициент вязкости ро не зависит от температуры. Поэтому равенство расходов для течения газа. Абеля — Нобля и совершенного газа, достигается при выполнении следующего условия:

ReiQi = Re2 Q2.

Здесь Rei, Qi — число Рейнольдса и безразмерный расход для течения газа Абеля - Нобля, Rei, Qi — соответственно для совершенного газа. Указанное равенство выполняется, например, для следующей комбинации параметров: Rei = 2687.35, Qi = 0.0147883 при Mi = 1.1 и Re2 = 2584.2, Q2 = 0.0153786 при M2 = 1.20577.

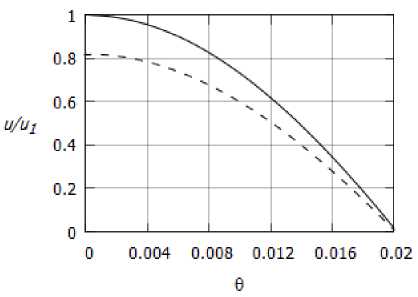
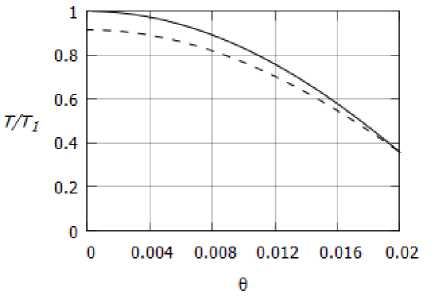
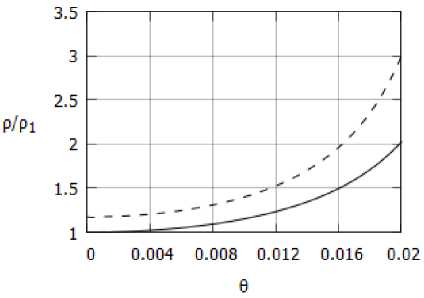
Сравнение распределения скорости, температуры и плотности в канале приведено на. рис. 4а, 46 и 4в соответственно. Численные величины отнесены к значениям газодинамических переменных в газе Абеля — Нобля на. оси симметрии.

Из приведенных рисунков можно сделать вывод, что при одинаковом расходе и температуре стенки скорость и температура, в газе Абеля — Нобля оказываются выше, чем в соответствующем течении совершенного газа. Из рис. 4в видно, что значение плотности в совершенном газе, особенно вблизи стенки, заметно выше, чем в газе Абеля — Нобля. Откуда следует, что тот же расход в совершенном газе достигается при меньшей скорости потока, чем в газе Абеля — Нобля (рис. 4а).

а)                                                         б)

в)

Рис. 4. Распределение а) скорости, б) температуры, в) плотности; пунктир — совершенный газ, сплошная линия — газ Абеля — Нобля

6.    Заключение

Рассмотрено течение типа Джеффри — Гамеля в плоском диффузоре для вязкого газа, подчиняющегося уравнению состояния Абеля — Нобля. Показано, что система уравнений Навье — Стокса в этом случае сводится к системе обыкновенных дифференциальных уравнений при условии постоянства коэффициентов вязкости и теплопроводности, что имеет место в случае модели газа сверхтвердых сфер.

Аналитически рассмотрен случай течения газа в тонком клине а ^ 1 при малых дозвуковых скоростях. Полученное решение по форме оказалось совпадающим с известным течением Пуазейля. В общем случае система автомодельных уравнений решена численно. Показано, что при одинаковом расходе скорость и температура в совершенном газе меньше, чем в газе Абеля — Нобля. Установлено, что при значениях параметра Ьо, превышающих некоторую критическую величину, сверхзвуковое автомодельное течение в клиновидном диффузоре становится невозможным.