Автомодельные турбулентные течения вязкого газа в клине

Течение Джеффери-Гамеля от источника, массы (стационарное движение жидкости между двумя плоскими стенками, наклоненными под углом друг к другу) представляет собой один из немногих классических случаев, в котором удается построить точное решение уравнений Навье-Стокса. в вязкой несжимаемой жидкости [1]. В работах [2-6] впервые установлена, возможность построения точного решения для случая ламинарного течения вязкого сжимаемого газа, в клине и конусе. В [2] численно решена, задача, о течении газа, в конусе с граничными условиями проскальзывания для температуры и скорости, а. в [4,5] решена, аналогичная задача, с граничными условиями отсоса/вдува. на. стенках. В работе [6] задача решена как в автомодельной, так и в неавтомодельной постановке. Установлено, что автомодельные режимы течения могут быть реализованы в некоторой внутренней области конуса, конечной длины. В [7] получено аналитическое решение задачи о ламинарном течении газа, в клине, а. в работе [8] получено аналогичное точное решение для плоской струи

вязкого газа от линейного источника импульса. В частном случае, когда температура газа постоянна вдоль линий тока, а коэффициенты переноса - степенные функции температуры, построены аналитические решения. В [9] впервые рассматривается автомодельное турбулентное течение вязкого газа в конусе. Проведено численное решение системы нелинейных обыкновенных дифференциальных уравнений, описывающих автомодельное турбулентное течение; полученные результаты сравниваются с аналогичным ламинарным течением [10].

В настоящей работе изучается возможность построения автомодельных решений для случая турбулентного течения сжимаемого газа в клине. Показано, что при определенной комбинации определяющих параметров задачи уравнения Навье-Стокса, осредненные по Фавру, могут быть сведены к системе обыкновенных нелинейных дифференциальных уравнений.

2.    Постановка задачи

Рассмотрим стационарное турбулентное течение вязкого сжимаемого газа от источника массы, расположенного в вершине клина с полууглом раствора а (рис. 1).

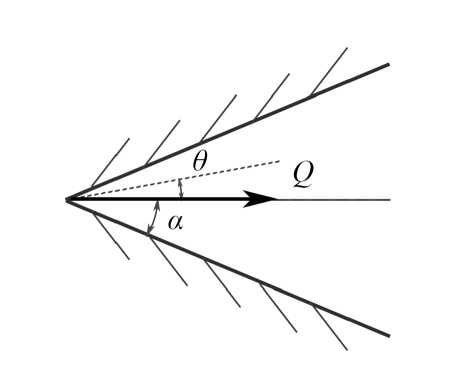
Рис. 1. Схема течения газа в клине

В полярных координатах (г, 0) уравнения Навье-Стокса, осредненные по Фавру, имеют вид [11]:

9 (грн) 9г

= 0,

р«^ = - ^ +1 Г9 г ст■ ^)) + 9 .. .. + о^) _ өө , 9г 9г г        9т9г

1 9р + 1 9 (г2 (атӨ + отгө)) + 1 9 (стөө + сттөө) г 90   г2       9гг 90

рТиіг =1 f Ак+ктНТ)+4 Т ((”+кт)+<

9г г 9г у         9г}   г2 9090 у

, 0 ⁺ 0т. 22 , q 2 ,    21   ²⁽0 + 0т ) / 1 ^{9 (гИ}) V

+    2 L^rr + SӨӨ + 2^гӨ 1        3 I г ~г^•

Здесь использованы стандартные обозначения для термодинамических переменных: р, Т, р, S — соответственно плотность, давление, температура и энтропия единицы массы; 0 — коэффициент сдвиговой вязкости, к — коэффициент теплопроводности. Течение в конусе предполагается радиальным, так что вектор скорости V = (и, 0). Компоненты тензора напряжений ст определяются следующими соотношениями:

ст _Тт = р S _тт — 2^-1- (ru); ст өө = р Sөө — ^ту- (ru); ст _тө = р S _гө , 3r dr                   3r dr

S„ = 2 £ ;Sөө = 2 ^u;S„ =1 Or         r        r OU

Тензор турбулентных напряжений стт и турбулентный тепловой поток qт согласно гипотезе Буссинеска [11,12] представляются в следующем виде:

стттт = ^ t S _Tt —     уг (ru); сттөө = РтSөө - ²г^д~(ru); сттгө = РтS_rө ,

3r dr                     3r dr qт = —кт VT.

В соответствии с теорией пути смешения Прандтля, коэффициент турбулентной вязкости р_т, определяется по формуле:

pt2

Рт = — r

Эи дө

где I — длина пути смешения. Турбулентный коэффициент теплопроводности кт связан с рт известным соотношением:

Число Прандтля Pr в одноатомном газе близко к 2/3 [13], поэтому далее принимаем р/к = 4/15R, где R — универсальная газовая постоянная. Турбулентное число Прандтля Ргт для простоты будем считать постоянным и равным Ргт = 1. Отметим также, что коэффициенты переноса предполагаются степенными функциями от температуры. В случае более сложной зависимости коэффициентов переноса от температуры, например, при выполнении закона Сазерленда, автомодельного решения отыскать не удается.

Выберем в качестве масштабов значения газодинамических параметров po, uo, To в некоторой произвольной точке на оси конуса r = ro, Ө = 0 и перейдем к безразмерным переменным: pi, к, T, р, r. Полученные уравнения движения содержат следующие параметры: число Прандтля, отношение теплоемкостей у = Ср/с^, число Рейнольдса Reo = pouoro/po іі число Маха, Mo = uo/VyRTo. где ^тісрсз po обозначено значение вязкости при T = To. Р = po(T/To)^k.

3.    Вывод определяющих уравнений

В общем случае автомодельное решение для осесимметричного турбулентного течения газа, по аналогии с «ламинарным» случаем будем искать в виде [7]:

u(U) _    р(Ө)                          T (Ө) _    /T (Ө)\k _ у u = ---; р = ——у; p = rm p(U); T =  —; p = ( I ; к = ——-----p.   (6)

)m ’ ¹     r^m+1  '          r\ n       r2m ^{1 1}    \ )2m / ’ Pr(1 _ У )       ^V

Показатель степени переменной к в (6) для плотности подбирался так, чтобы уравнение неразрывности (1) выполнялось автоматически, а. для давления степень определялась из уравнений импульсов (2) и (3):

__du   Эр 1

pu— « — « Я-гл-dr   dr   r^m+²

Показатель степени r для температуры подбирался из уравнения состояния, записанного с учетом выбора, масштабов:

?М2р(ө) = р(ө)Т ( ө ) .

В выражении (5) присутствует неизвестный параметр I. В плоском радиальном течении выражение для длины пути смешения согласно теории Прандтля принимает вид [11,12]:

I = _Xr(a - | Ө | ) .

В формуле (8) х ^— некоторый коэффициент, числовое значение которого определяется с использованием экспериментальных данных. Окончательно выражение (5) можно переписать в следующей форме:

W = р ( Ө ) х ²( « — | Ө | )²

Ои(ө) аө

откуда заключаем, что слагаемые в уравнениях (2) - (4), отвечающие за турбулентную вязкость, имеют порядок:

ст 1

— « ^ , О .

Г     г^т+²

Оценим теперь порядок «вязких» членов в уравнениях (2) - (4):

a

∝ г

1     1

г2тк гт+2 ‘

(И)

Легко видеть, что выражения (7), (10) и (11) имеют одинаковую степень г при выполнении условия:

2тк = 0 .

После подстановки соотношений (6), (8) в уравнения (2) - (4) получим следующую нелинейную систему обыкновенных дифференциальных уравнений:

^{(т + 1)}р + ттгрп ² +      [^4(т2 - ¹⁾ п^Тк + -° ^ТТ^к 1 +

Reo [3                аӨ у аӨ/J

⁺ х ² 3 ⁽ т ^{2 - 1)}р⁽а ^{-| ө | ) 2} и

адө ) аө

⁺ аө f^{p(a - | ө | )}2 аө у

dti(W) du\ аө ай)

=0

dp 1

аө Re o

+ х ² [ (1 — т ) р ( "-К^

du 2 .        . d

^{(1 - т)Т} Тө ⁺ з ^{(т + 2)} Тө^ ^{к и}) ⁺

+ 2 ⁽ т + 2)d» '" -і ө )² " 1 и)1 3 аө у             аө у

up (1 - ^ M        И ^к +1 + Цт.%) ] +

+     Т^ки² ( т ² + т + 1) +     ( du У +

3Re o                    Re o у dӨ

+              [4т2Тр(" - |ө|)2 ^иіө) +   (р(„ - |ө|)2 ^ ОТ 11 + могіт(^ — 1)                    оө оө у            оө оө у

+ х2р(а -|ө|)2 уу) [4и2(т2+т+1) + (аи 11 аө з                   уаөу с граничными условиями:

и(0) = 1; и(а) = 0; Т(0) = 1; Т(а) = T_w ; р(0) =

7 М2 ‘

Для практических расчетов требуется знать числовое значение параметра у. В работах [14,15] для осесимметричных турбулентных течений сжимаемого газа принято у = 0.4. С учетом этого окончательно получаем замкнутую краевую задачу (13) - (16), которая описывает автомодельные турбулентные течения вязкого газа в клине.

4.    Течение в тонком клине

Рассмотрим подробнее частный случай течения в тонком клине, когда полуугол раствора а ^ 1. В этом случае исходную систему уравнений (13) - (16) удается существенно упростить. Действительно, пусть Мд к а ^ 1 и Reg к 1, так чтобы выполнялось условие сплошной среды, а именно число Кнудсена Kn = Mg/Reg ^ 1. Представим основные газодинамические параметры в виде рядов по степеням а:

и(Ө, а) = ид(Ө) + аи1(Ө) + ...,

^^^^.

Р^{(0, а)}

ид(Ө) + аи1(Ө) + ... 7Мд

—             —          —

Т(Ө, а) = Тд(Ө) + аТі(Ө) + ..., где Ө = Ө/а. После подстановки этих выражений в (13) - (16) для нулевого приближения получим следующую систему обыкновенных дифференциальных уравнений:

^рд ।      ¹    '•      ₀. "^р о- '^/2/ м

7М2 + а2Reg d02 ~ 0; ДӨ ~ 0;  d02 ~ 0’ решение которой с учетом граничных условий (16) имеет простой вид:

рд = 1; Тд = 1; ид = 1 -

Ө2.

При этом должно быть выполнено следующее условие автомодельности:

Rega2 _ 7 М2 =2.

Заметим, что аналогичное условие Reg/7М2 = 4/3+1/(1-сова), полученное в работе [7] для произвольного угла в «ламинарном» случае, при а ^ 0 в точности совпадает с условием (17). Решение для следующих членов разложения имеет вид ui = y2Reg [4/3(Ө3 - 1) - 2(Ө4 - 1) + 4/5(Ө5 - 1)] ; Ті = 0; рі = 0, а условие автомодельности принимает форму: Reg(a2/27M2 - 2ау2/15) = 1.

Отметим, что для тонкого клина в нулевом приближении отсутствует зависимость решения от параметра турбулентности у, поэтому оно совпадает с соответствующим решением (типа Пуазейля) для ламинарного течения [7]. Влияние турбулентности начинается с первого приближения.

5.    Численное исследование автомодельного решения

Систему нелинейных дифференциальных уравнений (13) - (16) решить аналитически в случае произвольного полуугла а не представляется возможным. Далее мы будем рассматривать систему (13) - (16) при к = 0 и т = 0. При этих значениях параметров к и m в случае ламинарного течения имеется достаточно простое аналитическое решение [7]. Численный метод [16], с успехом примененный к задаче турбулентного течения газа в конусе [9], может быть также использован и для системы (13) - (16), решение которой зависит от чисел Mo и Reo на оси клина, температуры стенки Т,_ш и полуугла раствора клина а. Для каждого значения а задавался некоторый набор значений чисел Mo, а значения Reo и Т,_ш подбирались таким образом, чтобы выполнялись граничные условия (16).

Оказалось, что в «турбулентном» случае в отличие от «ламинарного» автомодельное течение существует только в ограниченном диапазоне значений числа Mo. Обратимся к зависимости Reo = Reo(Mo) и T_w = T_w (Mo) при фиксированном а = 0.1 рад (см., соответственно рис. 2а, рис. 26). При значениях Mo, превышающих некоторое критическое значение, решение найти не удается. График зависимости M*(а) представлен на рис. 3. Заметим, что ограничение на значения полуугла а имеет место как в ламинарном, так и в турбулентном случае. При а ^ т/2 давление газа становится отрицательным, что противоречит термодинамическому условию р > 0. Аналогичное поведение решения при а ^ ^/2 наблюдалось и в ламинарном течении [7], которое в отличие от турбулентного существует при сколь угодно больших Mo.

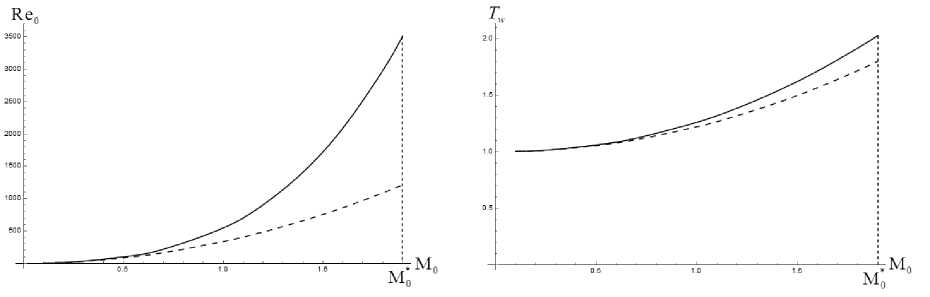
а)                                                         б)

Рис. 2. Зависимость Reo и Tw от числа Маха на оси клипа в турбулентном (сплошная линия) и ламинарном (штриховая линия) случаях

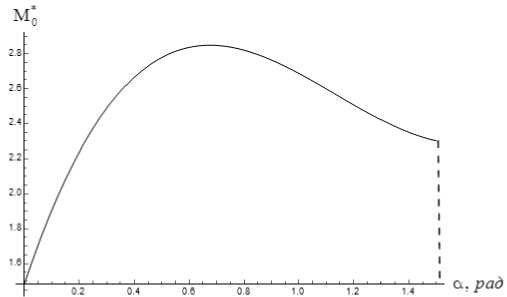
Рис. 3. Зависимость критического числа Маха M0 на оси клипа от полуугла раствора а

Сравним профили скорости и температуры ламинарного и турбулентного течений при одинаковом расходе на примере клина с полууглом раствора а ~ 60. Расход газа вычисляется по формуле:

Q = роиого • L • р^и^сІӨ = ReoTyo • L • Qo. J —a

Здесь L — «ширина канала», которую для простоты будем считать равной единице. Для сравнения выберем ламинарный режим с параметрами: Q o l = 5.57 • 10^-2, Mol = 1.8, ReoL = 1088, T _wl /T o l = 1.72, и соответствующий, близкий к нему, турбулентный режим: Q o t = 6.69 • 10^-2, MoT = 1.2, ReoT = 904, Т_шТ/Тот = 1.39. Отсюда можно получить отношение скоростей потока турбулентного и ламинарного режимов течения: ит /b- l ~ 0.74. Графики полученных зависимостей представлены на рис. 4а, рис. 46.

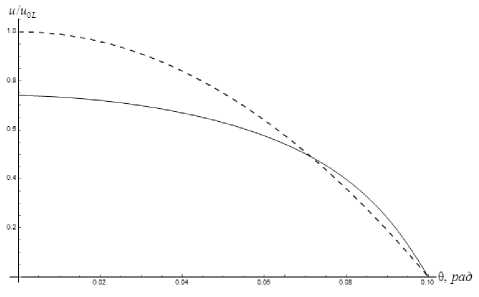
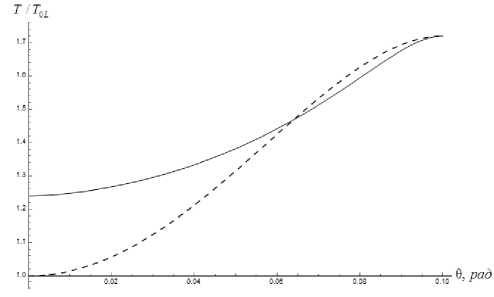
а)                                                         б)

Рис. 4. Профили скорости и температуры в турбулентном (сплошная линия) и ламинарном (штриховая линия) случаях

Как видно из представленных зависимостей, усредненная скорость в турбулентном течении ниже, чем в ламинарном, а усредненная температура выше. Это можно объяснить тем, что в турбулентном течении часть кинетической энергии переходит в энергию турбулентных пульсаций. Дальнейшая диссипация энергии приводит к увеличению средней температуры турбулентного потока.

6.    Заключение

Установлена возможность построения автомодельных решений для стационарного турбулентного течения газа от источника массы в клине. Для случая течения в тонком клине получено асимптотическое решение. В общем случае произвольного угла раствора клина проведено численное исследование. В результате установлено, что в отличие от ламинарного случая, для турбулентного течения газа решение существует лишь в ограниченном диапазоне определяющих параметров. Максимально возможное число Маха приближенно равно Mo ~ 2.8.