Автомодельные закономерности стадийности разрушения и степенные законы роста усталостных трещин

ВЕСТНИК ПНИПУ. МЕХАНИКА № 5, 2024PNRPU MECHANICS BULLETIN

Положения механики разрушения, основанные на введении структурных масштабов, характеризующих формирование областей разрушения в вершинах трещин (Finite Fracture Mechanics – FFM, Theory of Critical Distances – TCD) [1], рассматриваются на основе развитых представлений о закономерностях стадийности переходов к разрушению в поврежденной среде как специального типа критических явлений в средах с дефектами – структурно-скейлинговые переходы [2]. Эти сингулярности представляют собой промежуточноасимптотические автомодельные решения и могут быть предложены в качестве физической основы для интерпретации предположений «механики конечных разрушений», теории критических дистанций, эффектов не-локальности в стадийности развития поврежденности, зарождения малых трещин и распространения трещины при ее взаимодействии с областями локализации по-врежденности (дочерними трещинами) в когезионной зоне (Process Zone) [3]. Критические дистанции при этом определяются как характерные масштабы локализации повреждений, связанные с коррелированной динамикой автомодельных коллективных мод дефектов [4].

Два типа автомодельных решений, связанных с сингулярностью напряжений Ирвина (коэффициент интен- сивности напряжений) и кинетикой локализации повреждений в виде коллективных мод в ансамбле дефектов, рассматриваются как «внутренние» и «внешние» механизмы, обеспечивающие сценарий развития разрушения при различных режимах нагружения [5]. Внутренние механизмы определяются свойствами материала, обусловленными универсальностью сценария локализации повреждений в окрестности вершины трещины [6]. Они контролируют кинетику поврежденности в когезионной зоне, включая локализацию поврежденности, формирование «дочерних трещин», взаимодействие последних с основной трещиной и ее распространение.

Характерной особенностью образования усталостной трещины является ее чувствительность как к внутренним (кинетика поврежденности), так и к внешним механизмам, определяющим особенности напряженного состояния в вершине трещины. Для описания механизмов роста усталостных трещин для пластичных и квазихрупких материалов предлагаются феноменологические кинетические уравнения, отражающие степенные закономерности роста трещин da / dN от приращения ∆K или максимального значения K max коэффициента интенсивности напряжений в вершине трещины [7].

dN = ^C ( ^K max ) n ( ^ K ) m ,

где C – кинетический коэффициент; показатели степени n и m отражают различную чувствительность к ∆K для вязких материалов и к K max для квазихрупких материалов. В рамках механики разрушения эта зависимость используется для прогнозирования долговечности материала при известном напряженном состоянии в терминах напряжений σ (коэффициента интенсивности напряжений K ), начального a размера трещины, геометрии и свойств материала (предела текучести σ y и тре-щиностойкости K 1 c ).

В модели разрушения [7] пространственные масштабы вводятся двумя методами: (1) как физические масштабы, связанные с микроструктурой материалов (размеры зерен, включений), и (2) как масштаб когезионной зоны (зоны процесса), характеризующий масштаб локализации поврежденности, определяющий распространение трещины. Обычно используемый масштаб когезионной зоны L определяется как

L = 1 [ K c-} ^П1° u )

,

здесь K c – вязкость разрушения материала, σ u – предел прочности при растяжении.

Задачи на исследование усталости материалов включают аналогичное кинетическое уравнение с использованием материальных констант с соответствующими циклическими параметрами: вместо σu и Kc используются значение порогового коэффициента интенсивности напряжений ∆Kth и значение критического коэффициента интенсивности напряжений ∆Kc. Константа L применяется в соответствии с методами, основанными на определении напряжений или интенсивности напряжений при данных условиях нагружения [2]. В этих моделях разрушение происходит при достижении трещиной длин, при которых значение коэффициента интенсивности напряжений достигает значения критической интенсивности напряжений ∆Kc при достижении длины L. Основанием для введения критического масштаба L в единицах коэффициента интенсивности напряжений является существование промежуточного автомодельного решения (по Ирвину) для поля напряжений в вершине трещины упругого материала, ∆Kth и ∆Kc. Однако оба предельных значения являются следствием двух различных механизмов в зоне процесса вблизи вершины трещины, обеспечивающих распространение трещины по сценариям «вязкого» и «ква-зихрупкого» разрушения. «Вязкий» сценарий соответствует развитию трещины по закону Пэриса с соответствующим степенным показателем (близким к четырем). «Квазихрупкие» разрушения характеризуются более высоким степенным показателем. Существует связь между пороговыми значениями ∆Kth и ∆Kc, величиной показателя степени и механизмами, управляющими стадиями развития усталостной трещины. Показатели степени связаны с «ведущими» механизмами, обеспечивающими «высвобождение» свободной энер- гии в когезионной зоне в процессе накопления повре-жденности. При «вязком сценарии» возникают многочисленные полосы скольжения (PSB), кинетика зарождения и взаимодействие между которыми определяют пороговое значение ∆Kth и величину степенного показателя в законе Пэриса. Исчерпание «пластического ресурса» в когезионной зоне приводит к зарождению микротрещин, формированию «дочерних трещин» и распространению основной трещины. Кинетика ее распространения определяется пороговым значением ∆Kc с более высокими показателями степени. Коррелированное поведение PSB и областей локализации повреждений (усталостных бороздок) [7; 8] отражает автомодельные закономерности распространения трещин в соответствии с характерными показателями степени для ∆Kth и ∆Kc. Степенные кинетические законы, характеризующие стадийность распространения трещин, являются следствием автомодельных решений, определяющих распределение напряжений в вершине трещин (в терминах коэффициента интенсивности напряжений) и кинетику накопления по-врежденности в когезионной зоне.

Структурные масштабы L , определяющие критические условия распространения трещины, могут быть выявлены на основе соотношений баланса энергии [3]

£ 2 L K ² da = K ] ■ 2 L . (3)

Соотношение (3) отражает теоретическую концепцию «Механики конечного разрушения» и «Теории критических дистанций» [1] основанную на введении конечного масштаба «зоны процесса», определяемого микроструктурой и напряженным состоянием материала [2]. Для металлов в условиях усталости L соответствует длине зоны процесса, связана с микроструктурными свойствами (например, с размером зерна), влияющими на локализацию пластической деформации (формирование ансамбля PSB), и ее трансформацию в зоны разрушения. Для квазихрупких материалов и композитов L приближается к размеру зоны локализации повреждений [4; 8; 9]. Концепции «Механики конечного разрушения» и «Теории критических дистанций», основанные на введении масштаба L и σ 0 (σ 0 >> σ u ) в качестве характеристики прочности материалов, обеспечили более глубокое понимание закономерностей разрушения с учетом моделей когезионных зон и эффектов нелокальности в рамках традиционных феноменологических переменных и их критических значений.

2. Интерпретация диаграммы Батиаса – Пэриса

Особенностью сверхмногоцикловой (гикацикловой) [10] усталости является образование трещины внутри материала, что делает её особенно опасной, например в лопатках турбин авиадвигателей [12–15]. Внутренние трещины не диагностируются традиционными методами неразрушающего контроля, и когда они достигают критических размеров, происходит внезапное разруше- ние конструкции [15]. Роль сингулярностей, связанных с промежуточно-асимптотическими решениями, можно проиллюстрировать диаграммой роста усталостной трещины Батиаса – Пэриса [16; 17], представленной на рис. 1, где показаны оба сценария перехода от повреждения к разрушению, в терминах приложенных напряжений и интенсивности напряжения.

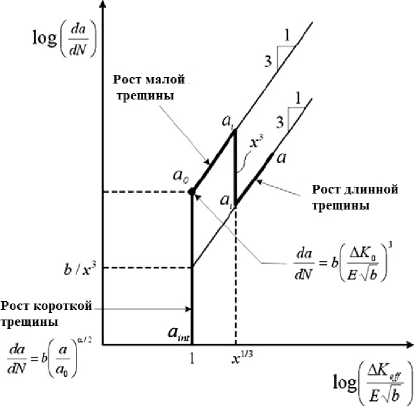
Рис. 1. Диаграмма распространения трещины в HCF [14; 15]: b – вектор Бюргерса, ∆K 0 и ∆K eff – коэффициенты интенсивности напряжений, соответствующие длинам трещин a 0 и a 1

Fig. 1. Crack advance diagram in HCF [14; 15]: b is the Burgers vector, ∆K 0 and ∆K eff ΔKeffare stress intensity factors corresponding to the crack lengths a 0 and a 1

На диаграмме видно, что рост «малых» трещин определяется кинетическим уравнением Херцберга, которое чувствительно к структурному параметру – вектору Бюргерса, а развитие основной трещины Пэриса определяется кинетическим уравнением Пэриса (4). Параметр x определяет точку перехода между сценариями роста «малых трещин», роста трещин Пэриса и зависит от условий нагружения, размера трещин, кинетики (стадийности) поврежденности, определяемых зарождением и взаимодействием зон локализации пластической деформации (PSB) и поврежденности. В [18] показана связь стадийности поврежденности с двумя типами автомодельных решений для параметра поврежденности (деформации, индуцированной дефектами), имеющими природу автосолитонных мод и диссипативных структур обострения. Кинетика зарождения, распространения и трансформации этих мод связана с качественными изменениями неравновесного (метастабильного) термодинамического потенциала (неравновесной свободной энергии) материала с дефектами, следствием которых является формирование коллективных мод дефектов (автосолитонной и обостряющейся природы), локализованных на соответствующих масштабах. Это позволяет объяснить переход от зарождения и роста малых трещин к инициированию и распространению усталостной трещины с использованием двух критериальных значений ∆Kth и ∆Kc. Эти значения отражают определяющую роль двух различных механизмов в «зоне процесса» вблизи вершины трещины, обусловливающих распространение трещины по «вязкому» и «квазихрупкому» сценариям. «Вязкий» сценарий соответствует росту трещины по закону Пэриса с соответствующим (близким к 4) показателем степени. «Квазихрупкий» сценарий с более высоким показателем степени характерен для последней стадии развития усталостной трещины «охрупченного» материала. Существует связь между критическими значениями ∆Kth и ∆Kc, величиной показателя степени и механизмами, определяющими стадии усталостного разрушения. Показатели степени связаны с «ведущими» механизмами, обеспечивающими «высвобождение свободной энергии» (free energy release) в зоне процесса. При «вязком сценарии» наблюдаются многочисленные полосы скольжения PSB с автосолитонной кинетикой дислокаций. Их коррелированное поведение феноменологически связано с величиной ∆Kth и соответствует показателю четвертой степени в законе Пэриса. Последующая трансформация PSB в ансамбли микротрещин и их коррелированное поведение соответствует достижению порогового сценария ∆Kc распространения усталостной трещины с более высокими показателями степени. Согласованное поведение PSB и областей локализации повреждений объясняется трансформацией коллективных мод дефектов и соответствующих им автомодельных решений при качественном изменении типов метастабильности неравновесной свободной энергии материала с дефектами, которые критериально связаны с пороговыми значениями ∆Kth и ∆Kc и характерными показателями степени.

Область зарождения усталостной трещины, не зависящая от ∆K, соответствует «обостряющейся» кинетике локализации повреждений и переходам от структурно зависимых масштабов дефектов aint к «малым трещинам» с размерами a0, который совпадает с масштабом локализации коллективной моды дефектов – «структуры обострения» Lc. Степенной закон da/dn=b(a/a0)n/2 отражает автомодельную (взрывную) стадию кинетики повреждений на масштабе Lc, что позволяет определить a0 ~ Lc. Начиная с масштабов a0, кинетика разрушения определяется «дуальностью сингулярностей», связанных с коэффициентом интенсивности напряжений ∆K, и сингулярностями, определяющими зарождение PSB в виде автоволновых структур локализованной пластичности и «обостряющихся» структур локализованной поврежденности, описывающих зарождение «дочерних» трещин в когезионной зоне. Уменьшение скорости распространения трещины является следствием зависимости кинетики трещины от коэффициента интенсивности напряжений ∆K согласно закону Пэриса. Масштаб зоны процесса в этом случае связан с масштабами локализации множественных PSB c переходом к образованию очагов («дочерних трещин») с кинетикой режимов «с обострением» на спектре пространственных масшта- бов LH ~ к Lc (к = 1, 2, …). При этом основным «диссипативным» фактором для пластичных материалов является формирование множественных PSB.

Закономерности перехода от усталостного повреждения к распространению усталостной трещины, определяемые обсуждаемыми типами автомодельных решений, отражаются на морфологии поверхности разрушения и могут быть идентифицированы на основе вычисления масштабных инвариантов соответствующих областей поверхности разрушения. Методика вычисления масштабных инвариантов представлена в работах авторов [18–20] по данным профилометрии поверхности разрушения в терминах показателя Херста и соответствующих масштабов: расстоянием между дефектами l sc (близкого к вектору Бюргерса b на диаграмме Батиаса – Пэриса) и длины зоны процесса L pz. Эти длины соответствуют диапазону масштабов [ l sc , L pz ], соответствующих постоянным значения показателя Херста и характеризующих коррелированное поведение дефектов в зоне процесса L pz .

С учетом отношения -c^- << 1, характерного для LPZ неполной автомодельности, промежуточное асимптотическое уравнение для скорости трещины da/dN можно записать в виде [19]:

ские свойства: твердость 317 HB, предел текучести 970 МПа, предел прочности при растяжении 1018 МПа, модуль Юнга 211 ГПа, при комнатной температуре имеет предел усталости 600 МПа после 106 циклов при частоте 10 Гц.

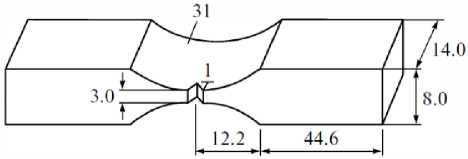
Усталостное симметричное растяжение – сжатие образцов из высокопрочной стали R5 (рис. 2, а ) проводилось на ультразвуковой усталостной испытательной машине при частоте 20 кГц. Испытательная установка (рис. 2, b ) состояла из следующих основных узлов: генератора, преобразующего колебания частотой 50 Гц в ультразвуковой электрический синусоидальный сигнал частотой 20 кГц; пьезоэлектрического преобразователя, генерирующего продольные ультразвуковые волны и оказывающего механическое воздействие на частоте 20 кГц; ультразвукового волновода, увеличивающего амплитуду механических напряжений в (рабочей) центральной области образца. Для предотвращения перегрева образца используется система воздушного охлаждения. Напряжение в центре образца задается программно управляемым перемещением свободного конца образца. Длина трещины измеряется с помощью оптической цифровой камеры.

da. = l ^к - Т ^dN sc [ Ej _?

^ K eff

= ^ K

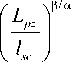
а

где α – показатель степени для области 2 (см. рис. 1) в диапазоне масштабов [ l sc , L pz ], соответствующей многомасштабной корреляции шероховатости, индуцированной дефектами, K th ~ E√l sc .

Масштабная инвариантность роста усталостных трещин в режиме сверхмногоцикловой усталости

b

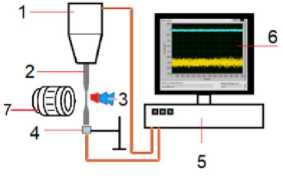
Рис. 2. Схематическое изображение образца (длина в мм): a – экспериментальной установки; b : 1 – волновод, 2 – образец, 3 – система охлаждения, 4 – датчик перемещения, 5 – система управления и    аналого-цифрового    преобразователя,

6 – программное обеспечение для анализа, 7 – объектив камеры для измерения длины трещины

Количественная фрактография представляет собой метод исследования поверхностей разрушения материалов, позволяющий получить количественные данные о процессе разрушения, из которых можно определить скорость роста трещин и дать оценку усталостной долговечности материалов [21]. В данной работе на основе морфологии поверхности разрушения определялись масштабные инварианты, связывающие степенные законы роста малых трещин и трещин Пэриса.

Испытания на рост усталостных трещин проводились на горячекатаной низколегированной стали R5 при симметричном растяжении (R = -1) в режиме I по методике, аналогичной стандарту ASTM E647. Материал представляет собой сталь, полученную после двойной закалки в воде на первом этапе при температуре 920 °C и на втором этапе при 880 °C, а затем выдержке при 650 °C с охлаждением водой. После такой термообработки материал демонстрирует следующие механиче-

Fig. 2. Schematic picture of the specimen with lengths in mm: a – and experimental setup; b : 1 – horn, 2 – specimen, 3 – cooling system, 4 – displacement sensor, 5 – controlling and analog-digital converter system, 6 – analyzing software, 7 – camera lens for measuring crack length

На первом этапе зарождалась усталостная трещина длиной ~1,5 мм и ее последующий рост контролировался путем изменения приращения интенсивности напряжения ΔK , рассчитанного по формуле для амплитуды нагрузки:

A K =   ^ №A o Y ( a / w ),         (5)

(1 -v2) \ a где E – модуль Юнга, ν – коэффициент Пуассона, A0 – амплитуда колебаний, Y – полиноминальный фактор, w – ширина образца. Полиноминальный фактор для заданной геометрии образца (см. рис. 2, а) был следующим:

Y ( a / w ) = 0,635( a / w ) + 1,731( a / w ) 2 -- 3,979( a / w ) ³ + 1,963( a / w ) 4 .

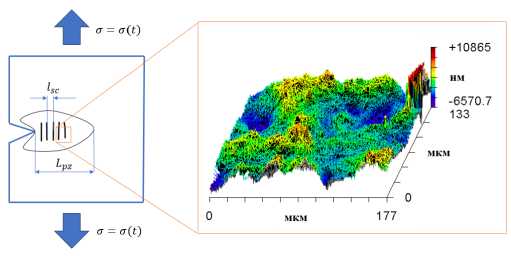
Рис. 4. Схематическое изображение зоны процесса у вершины трещины и типичное изображение шероховатости поверхности

После завершения эксперимента образцы подвергались охлаждению в жидком азоте с последующем вскрытием поверхности разрушения. Ее изображение представлено на рис. 3, где также приведены изображения областей продвижения трещины, полученные в результате изменения коэффициента интенсивности напряжения. Изменение коэффициента интенсивности напряжения привело к появлению тонкого следа на поверхности трещины, что позволило разделить ее на три области: 1 – область распространения малой трещины, 2 – область распространения длинной трещины Пэриса, 3 – область начальной трещины.

Рис. 3. Изображение поверхности разрушения (электронная микроскопия) стали R5, отражающее стадии развития трещины: 1 – область роста малой трещины, 2 – область роста длинной трещины, 3 – область начальной трещины

Fig. 4. Schematic image of the process zone at the crack tip and typical image of the surface roughness

Масштабный инвариант, выраженный через показатель Херста H , оценивался путем усреднения разности размеров шероховатостей z ( x ) на поверхности зоны процесса по формуле [20–22]:

(1/2)

C ( r ) = (Zz ( ^x + r ) — z ( x ))       « r^H .          (7)

x

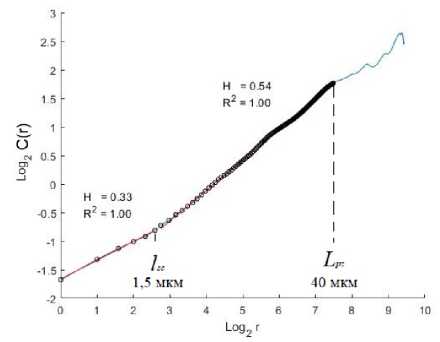
Логарифмический график log 2 C ( r ) ~ log 2 ( r ) позволил оценить показатель шероховатости как пространственный инвариант, соответствующий постоянному наклону в соответствующем диапазоне масштабов [ l sc , L pz ] (рис. 5).

Fig. 3. Fracture surface image (electronic microscopy) of the R5 st eel reflecting the crack advance staging: 1 – area of small crack growth, 2 – area of long crack growth, 3 – area of initial crack

Для определения масштабных инвариантов шероховатости, вызванной дефектами в зоне процесса (рис. 4), морфология поверхности излома исследовалась с помощью 3D-профилометра высокого разрешения (New View 5010) с разрешением по координате z 0,1 нм и по координатам x и y 0,5 мкм. Предполагается, что морфология поверхности излома может быть охарактеризована двумя масштабами. Первый, l sc , связан с длиной, на которой дефекты взаимодействуют друг с другом, образуя рельеф усталостной трещины, а второй, L pz – с размером зоны, в которой происходит это взаимодействие.

На каждом этапе распространения трещины были сделаны трехмерные изображения поверхности размером 133×177 мкм и проанализированы 13 одномерных профилей.

b

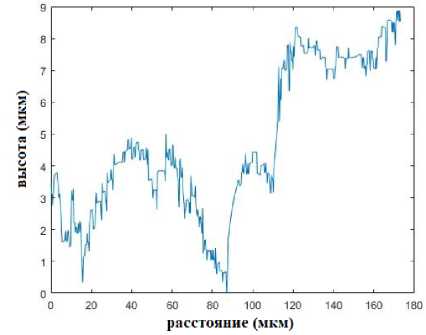
Рис. 5. Одномерный профиль шероховатости поверхности ( a ), График зависимости log 2 C ( r ) от log 2 ( r ) ( b )

Fig. 5. The one-dimensional surface roughness profile ( a ), the log 2 C ( r ) vs log 2 ( r ) plot ( b )

Разрешающая способность профилометра New View позволяет определить верхнюю и нижнюю границу степенного закона корреляции шероховатости. Значение нижней границы линейного участка функции C ( r ) принималось за величину критического масштаба l sc , то есть минимального пространственного масштаба в зоне процесса, на котором масштабно-инвариантные закономерности проявляются как масштаб, обусловленный дефектами структуры, a значение верхней границы L pz принималось как длина, связанная с максимальным масштабом коррелированного поведения дефектов, отраженная в шероховатости поверхности. Длина l sc определяет точку перехода от кинетики накопления повреждений к кинетике, соответствующей закону Пэриса и формированием критического расстояния (CD) длиной L pz (рис. 5, b ). Средние значения характерных величин l sc и L pz , полученные по измерениям одномерных профилей поперечного сечения на различных этапах распространения трещины, представлены в табл. 1

Таблица 1

Условия испытаний, характерные масштабы l sc , L pz и показатель Херста H на различных стадиях развития трещины

Table 1

Test conditions, characteristic scales l sc , L pz and the Hurst exponent H for different stages of crack advance

∆ K , MPa m	∆ a , m	D N , циклы	l sc , мкм	L pz , мкм	H
6,200	6,80^10-4	2,05^106	1,7 ± 0,8	28,2 ± 7,5	0,41 ± 0,04
5,890	2,00^10-4	2,82^106	0,9 ± 0,3	38,1 ± 7,1	0,49 ± 0,03
5,596	3,20^10-4	4,74^105	1,7 ± 0,7	34,1 ± 8,6	0,41 ± 0,04
5,316	2,20^10-4	4,22^105	0,9 ± 0,3	38,2 ± 11,9	0,43 ± 0,03
5,050	2,60^10-4	7,37^105	1,3 ± 0,5	34,1 ± 7,3	0,44 ± 0,03
4,797	1,60^10-4	2,75^105	1,3 ± 0,5	42,2 ± 10,9	0,50 ± 0,02
4,558	3,20^10-4	7,13^105	1,4 ± 0,5	31,1 ± 4,7	0,52 ± 0,02
4,330	4,93^10-4	4,33^107	1,3 ± 0,5	39,5 ± 6,8	0,47 ± 0,03

Данные по шероховатости, полученные с помощью 3D New View (см. рис. 5), показали наличие двух характерных масштабов – масштаба зоны процесса L pz и корреляционной длины l sc , то есть масштаба, соответствующего началу корреляционного поведения, обусловленной дефектом шероховатости. Подстановка масштабов l sc и L pz из табл. 1, в уравнение (4) позволяет оценить показатель степенного закона на различных стадиях развития трещины. Показатель α ~2,51 соответствует линейному наклону для небольшого роста трещины, определяемого в основном окружной зоной повреждения (рис. 6). Показатель α ~3,88 характерен для трещины, растущей по закону Пэриса, и определяемой в основном асимптотой интенсивности напряжений.

Критическое расстояние при усталостном нагружении стали R5 соответствует значению L eff ~ L pz ≈ 38 мкм для трещины по закону Пэриса и пороговому коэффициенту интенсивности напряжений ∆ K th ≈ 4,33 МПа√м. Подставив экспериментальные данные для L pz и ∆ K th в уравнение (2), можно найти значение предела усталости для стали R5.

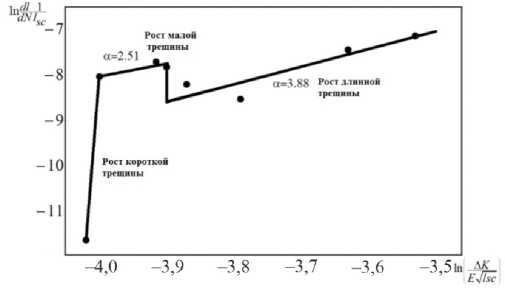
Рис. 6. Характерные графики зависимости ln от <  dNl sc J

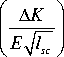
для различных стадий распространения трещины

( dl 1 I , I A X

Fig. 6. Characteristic plots In vs lnl---=

I dNlsc J     [ E^^^

for different staging of crack advance

Предел усталости, полученный по этой формуле для стали R5, равен σ o ≈ 396 МПа, что на 4 % больше экспериментально найденного предела усталости при испытаниях на сверхмногоцикловую усталость, представленном в [25] (σ o ≈381 МПа, R =-1, на воздухе и при комнатной температуре, N c ~10⁹ циклов). Высокочастотные условия нагружения дают уникальную возможность изучить роль различных факторов и механизмов локализации повреждений и распространения трещины. Качественное отличие малой трещины и трещины, растущей по закону Пэриса, отражается в значениях показателей степени и соответствующих основных механизмах, ответственных за локализацию повреждений в области зоны процесса. Показатель степени α~2,51 определяет ведущую роль автомодельного решения в виде структур «обострения» для кинетики малой трещины, а значительные изменения основных механизмов и показателя степени α~3,88 – для трещины Пэриса, когда локализация повреждений в зоне процесса является следствием коэффициента интенсивности напряжений в области вершины трещины.

Кинетические закономерности роста усталостных трещин в алюминиевом сплаве АМг6 при комбинированном динамическом и последующем сверхмногоцикловом нагружении

Влияние случайных статических или динамических нагрузок на долговечность материалов в условиях сверхмногоцикловой усталости вызывает в настоящее время большой интерес в авиационном моторостроении в связи с необходимостью решения проблемы надежности (долговечности) в условиях эксплуатации лопаток газотурбинных двигателей при соударении с твердыми частицами, получившую в западной литературе определение foreign object damage [26–30].

Предварительное нагружение образцов из сплава АМг6 осуществлялось динамическим растяжением на разрезном стержне Гопкинсона – Кольского [31] при скоростях деформации до ~10³ c^-1 с последующим сверхмногоцикловым нагружением на ультразвуковой испытательной машине Shimadzu USF-2000 (см. рис. 2, b ) и количественным анализом фрактографии изломов на основе данных профилометрии.

Образцы, подвергнутые предварительному динамическому деформированию, приводились к необходимой геометрии в соответствие с методикой испытаний сверхмногоциклового нагружения. Усталостное нагружение с частотой 20 кГц осуществлялось при уровнях напряжений 105–162 МПа с коэффициентом асимметрии R=-1.

Циклическое нагружение при указанных режимах на базе ~109 циклов до разрушения показало снижение до ~25 % предельного напряжения разрушения предварительно нагруженного сплава АМг6 (112 МПа), по сравнению с исходным материалом (152 МПа в исходном недеформированном состоянии).

При усталостных испытаниях сплава АМг6 наблюдались два типа разрушения образцов. Первый, когда образцы разрушались непосредственно во время эксперимента. Второй, когда образцы, обладающие явными признаками разрушения (сильное изменение резонансной частоты испытаний, выход усталостной трещины на поверхность), уже были не способны продолжать выдерживать усталостную нагрузку на резонансной частоте. Поверхность разрушения образцов первого и второго типов «вскрывалась» охлаждением образцов жидким азотом при последующем «доломе». Предполагалось, что поверхность разрушения в режиме гигацикловой усталости уже сформировалась в процессе эксперимента и занимает большую часть поверхности разрушения, что сопровождается изменением резонансной частоты испытаний.

При разрушении цилиндрических образцов за число циклов, соответствующих базе многоцикловой усталости (106–107), трещина образуется с поверхности образца. При разрушении предварительно нагруженных образцов из сплава АМг6 на базе 108 циклов и более наблюдалось формирование трещины внутри образца, и на поверхности разрушения видна характерная для такого режима усталости область излома – «рыбий глаз» (fish-eye), в центре которой находится очаг разрушения, окруженный областью с фрагментированной (субмикрокристаллической) структурой (светлая область) (рис. 7).

Количественный анализ морфологии поверхностей разрушения проводился на интерферометре-профилометре New-View 5010. Области сканирования распределялись по зоне роста усталостной трещины (рис. 8) и анализировались одномерные образы-срезы рельефа поверхности в радиальном направлении по отношению к границе раздела между зонами 1 и 3.

Ряд одномерных «срезов» анализировался в пределах каждого «окна», обеспечивая представительность данных о структуре рельефа, индуцированного дефектами, с вертикальным разрешением ~ 0,1 нм и горизонтальным ~ 0,1 мкм.

а

b

Рис. 7. Характерный рельеф поверхности зоны усталостного разрушения сплава АМг6: а – образец №2 (σ a =120 МПа, N = 7,82 ⋅ 10⁸); b – образец №1 (σ a =138 МПа, N = 7,51 ⋅ 10⁸)

Fig. 7. Characteristic relief of the surface of the fatigue fracture zone of the AMg6 alloy: a – specimen No. 2 (σ a =120 MPa, N = 7.82 ⋅ 10⁸); b – specimen No. 1 (σ a =138 MPa, N = 7.51 ⋅ 10⁸)

Для определения минимального (критического) масштаба l sc , соответствующему установлению длиннокорреляционных взаимодействий в ансамблях дефектов, использовался метод определения показателя Херста. По одномерным профилям рельефа поверхности разрушения вычислялась функция C ( r ) по формуле (7).

Сравнение масштабов коррелированного поведения шероховатости рельефа поверхностей разрушения образцов, нагруженных в условиях много- и гигацикловой уста- лости, позволило установить существенное уменьшение верхней границы пространственных масштабов, на которой показатель Херста остается постоянным для динамически преднагруженных образцов в зоне fish-eye (рис. 9).

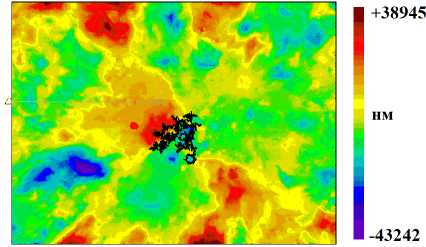
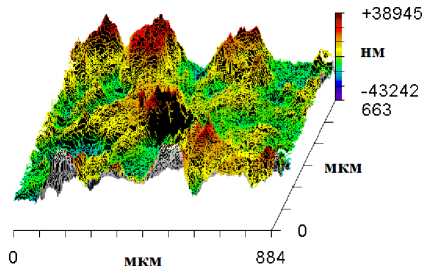
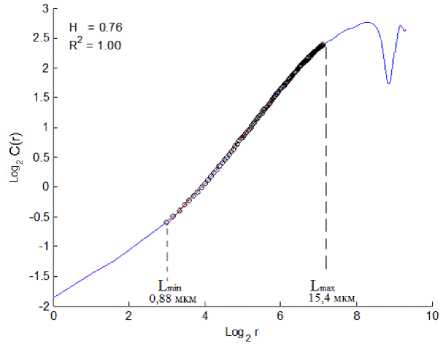
b

Рис. 8. Морфология поверхности разрушения (увеличение ×80), образец АМг6 №2 (σ a =120 МПа, N = 7,82 ⋅ 10⁸): а – карта высот; b – 3D-образ рельефа

b

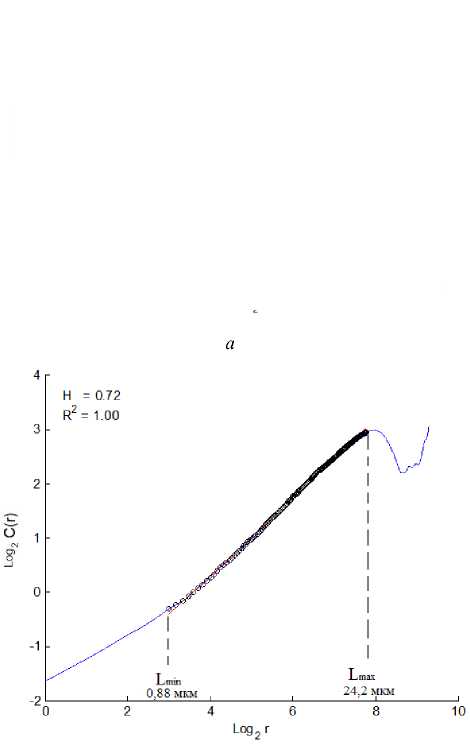
Рис. 9. Характерный вид зависимости log 2 C ( r ) от log 2 ( r ) образец АМг6 №2 (σ a =120 МПа, N = 7,82 ⋅ 10⁸): а – внутри fish-eye; b – вне fish-eye

Fig. 8. Morphology of the fracture surface (magnification ×80), specimen AMg6 No.2 (σ a =120 MPa, N = 7.82 ⋅ 10⁸): a – elevation map; b – 3D relief image

На поверхности разрушения можно выделить три характерные области: 1 – очаг разрушения, 2 – зона роста трещины внутри fish-eye, 3 – зона ускоренного роста трещины (см. рис. 7).

Радиусы соответствующих областей были измерены при помощи оптического микроскопа Hirox. Для образца № 10 (см. рис. 7, а ) они принимают следующие значения: зона 1 – l 0 = 76 мкм, зона 2 – l i = 270 мкм, зона 3 – l k = 2679 мкм.

Для разделения числа циклов, определяющих разные стадии, была применена методика анализа спектра колебаний свободного торца [19; 33]. Данная методика заключается в разделении сигнала с помощью быстрого преобразования Фурье по частотам колебаний и определению относительного коэффициента нелинейности βe, зависящего от амплитуды второй гармоники, которая связана с дефектной структурой [33; 34]. Чувствительность индукционного датчика перемещений позволяет уловить такие изменения в амплитуде колебаний, которые могут предсказать начало зарождения трещины (рис. 10).

Fig. 9. The characteristic type of dependence on the specimen AMg6 No.2 (σ a =120 MPa, N = 7.82 ⋅ 10⁸): a – inside the "fish-eye"; b – outside the "fish-eye"

Резкий всплеск амплитуды второй гармоники сигнализирует об образовании fish-eye, а её дальнейший рост связан с ростом усталостной трещины, как было показано с помощью рентгеновской томографии в работе [35]. На основе этой гипотезы сигнал разделили на три части, отделенные на рис. 10 разными цветами: синим выделено N1=7,43∙10⁸ число циклов, за которое сформировался очаг трещины, стадия формирования которого отделена резким скачком амплитуды второй гармоники. Число циклов, на протяжении которых трещина росла в зоне 2 (см. рис. 7, b ) отмечено зеленым цветом – это время между первым и вторым пиками на рис. 10, т.е. примерно N 2=1,4 ∙10⁶ циклов. Оставшиеся N 3=6,6 ∙10⁶ циклов трещина развивалась в режиме ускоренного роста трещины (зона 3 на рис. 7).

Во всех трёх зонах (см. рис. 7) при помощи интерферометра-профилометра NewView 5010 были вычислены значения l sc и L pz (табл. 2).

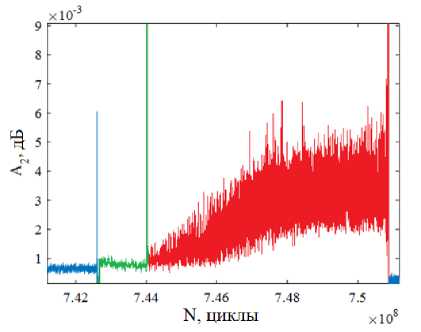
Рис. 10. Амплитуда второй гармоники для образца № 1. Синий цвет ( N = 7,426∙10⁸ циклов) – накопление повреждений и зарождение очага усталостной трещины. Зеленый цвет ( N = 1,4∙10⁶ циклов) – трещина росла внутри зоны 2, образовался fish-eye . Красный цвет ( N = 6,7∙10⁶) – трещина росла по закону Пэриса

N3 =

2

a

1 -

a

-

a-2

(1 к-в Lpz к lsc J

п

a

-a

Ac

l sc

. (10)

Константы α и β выбираются таким образом, чтобы при их значениях выражения (8)–(10) стали тождествами. В уравнениях (8)–(10) используются значения l sc и L pz , соответствующие областям 1 , 2 и 3 . Для нахождения α и β решаются задачи оптимизации численно в программном пакете Wolfram Mathematica:

N 1

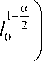
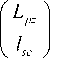
a п 2

Ac

a - 2

l sc

^ min, (11)

a > 0, в > 0

Fig. 10. The amplitude of the second harmonic for specimen No. 1. Blue color ( N = 7.426∙10⁸ cycles) – accumulation of damage and the emergence of a fatigue crack. Green ( N = 1.4∙10⁶ cycles – the crack was growing inside zone 2, a "fish-eye" was formed.

Red color ( N = 6.7∙10⁶) – the crack grew according to Paris' law

Таблица 2

Значения показателя Херста H и критических масштабов L pz и l sc для образцов с fish-eye

Table 2

The values of the Hurst index H and the critical scales L pz and l sc for samples with "fish-eye"

Номер образца	s, МПа	D N , циклы	Номер зоны	l , мкм sc ,	L pz , мкм	H
			1	0,6 ± 0,2	17,2 ± 2,2	0,63 ± 0,02
2	120	7,82^108	2	0,9 ± 0,2	26,3 ± 1,9	0,62 ± 0,02
			3	0,5 ± 0,2	26,2 ± 6,1	0,49 ± 0,02
			1	0,8 ± 0,2	11,6 ± 2,2	0,49 ± 0,02
1	138	7,51^108	2	2,2 ± 0,9	28,4 ± 3,5	0,51 ± 0,02
			3	0,4 ± 0,2	16,6 ± 1,7	0,60 ± 0,02

Для нахождения неизвестных констант α и β в уравнении (4) выполнялась следующая процедура. Подставим в уравнение (4) известные константы и число циклов до разрушения. Проделаем эту процедуру для образца № 1 для всех трёх ранее выделенных областей. Получим выражения для зарождения трещины (8) и её роста в области 2 (9) и области 3 (10):

a

2 0 ² - 1 0 2

- aV L

Л—в

a

-a

pz

a

l0

N 2

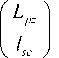
Ac

a - 2                 l_sc

a > 0, в > 0

N 3

^^^в

^ min, (12)

Ni =

к

a-2

a

^{2 1} 0

-

l

J к Scc J

a

l i ²

( L pz

к-в

п

к

l sc

a

Ac

El sc

-a

, (8)

N 2

к

J

к l sc J

п

к

Ac

El sc

J

a- 2

l sc

, (9)

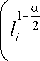
a - 2

a > 0, в > 0

L pz

l sc

-

в

a

(

п

к

l sc

Ac

к-a

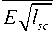
J

^ min . (13)

Значения α и β получились следующие: зона 1: α = = 2,82, β = 0,45; зона 2: α = 3,56, β =1,19; зона 3: α = = 6,25, β=1,38.

График скорости роста усталостной трещины от размера l 0 до l k изображён на рис. 11, а – для образца № 1, на рис. 11, b – для образца № 2.

Из данных рис. 11 видно, что предложенный подход позволяет описать эффект изменения скорости роста усталостной трещины при переходе от одной характерной области к другой. Константы, определённые для одного из образцов (образец № 1), дают удовлетворительное предсказание количества циклов до разрушения для других образцов. Например, для образца № 2: экспериментальное число циклов до разрушения – 7,82∙10⁸, предсказанное – 6,92∙10⁸ (относительная погрешность 11 %). Результаты расчёта для образца № 2 с константами α и β, полученными на образце № 1, дают качественно непротиворечивые результаты по числу циклов, ушедших на зарождение и рост трещины: 6,91∙10⁸ – на зарождение; 0,56∙10⁶ – на рост в зоне 2 ; 0,58∙10⁶ – на рост в зоне 3 .

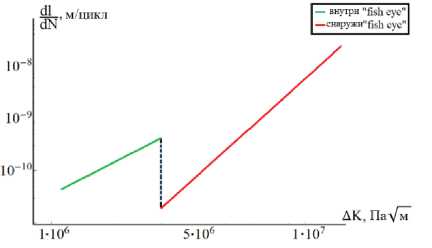
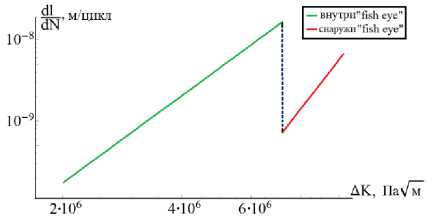
b

Рис. 11. Кинетическая диаграмма для: а – образец № 1; b – образец № 2

Fig. 11. Kinetic diagram for: a – specimen No. 1;

b – specimen No. 2

Заключение

Подходы механики «конечного» разрушения (Finite Fracture Mechanics), учитывающие масштаб когезионной зоны в окрестности вершины распространяющихся трещин, основаны на установленных закономерностях критичности стадийности поврежденности и перехода к разрушению. Закономерности критичности связываются с проявлениями дуальности механизмов, отражающих внешние (особенности напряженного состояния в вершине трещины) и внутренние (кинетика поврежден-ности формирование когезионной зоны) факторы. Дуальность механизмов связана с наличием двух автомодельных решений: автомодельное решение для распределения поля напряжений в вершине трещины (решение Ирвина) и промежуточно-асимптотические решения, описывающие стадийность развития поврежденности в «зоне процесса» как пространственно-временную сингулярную динамику локализации деформации при формировании автоволновых структур в ансамбле дефектов