Автомодельный характер полей вблизи вершины разреза в процессе ползучести в условиях аугментации поврежденности

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2025PNRPU MECHANICS BULLETIN

Введение. Современные численные методы реализации моделей процессов аккумуляции поврежденности при ползучести в материалах. Обзор

Ползучесть - важное и сложное явление, часто наблюдаемое при анализе разрушения инженерных материалов и компонент, работающих при высоких температурах, включая материалы, используемые в аэрокосмических и авиационных двигателях, конструкциях энергетической промышленности [1-7]. В инженерных и научных исследованиях понимание и прогнозирование явлений ползучести имеют решающее значение для обеспечения безопасности, надежности и срока службы конструкций и материалов [1-7]. Сложность механики ползучести обусловлена разнообразием ее физических основ. Микроструктура и организация материалов, диффузия атомов, дефекты кристаллической решетки, движение дислокаций и многие другие факторы играют важную роль в процессе ползучести. Эти сложные физические процессы приводят к нелинейности и временной зависимости деформации ползучести, что затрудняет создание точных механических моделей и соответствующих им расчетных схем. При описании деформации ползучести принято выделять первую, вторую и третью стадии ползучести. Наряду с этим для учета тесного взаимодействия различных механизмов и их взаимосвязей в последнее время уделяется большое внимание интеракции ползучести и усталости и их влиянию на процессы разрушения. На накопленную деформацию и развитие поврежденности при ползучести в значительной мере оказывают влияние температура, напряжение, время и внешние факторы - окружающая среда. Численное моделирование аугментации повреждений при ползучести в твердых телах создает значительные трудности из-за присущей этим явлениям сложности и зависимости от времени [1-7]. Повреждения при ползучести, характеризующиеся постепенной деформацией материалов под действием постоянного напряжения, особенно важны в инженерных приложениях, где важна долговременная целостность конструкции [1-7]. За последние десятилетия численные методы получили существенное развитие и нашли успешное применение в инженерных задачах [1-7].

Стремительное развитие компьютерных технологий и программного обеспечения значительно расширило применение методов численного моделирования в исследованиях разрушения при ползучести. Начиная с метода конечных элементов (МКЭ), постоянные инновации в различных методах и технологиях численного моделирования позволили исследователям более точно моделировать и прогнозировать сложные процессы разрушения при ползучести [8-18]. Эти достижения значительно снизили затраты на прогнозирование разрушения при ползучести и продолжают совершенствоваться, повышая точность и эффективность моделирования и стимулируя постоянное развитие исследований механизмов и процессов разрушения при ползучести. Компьютерное моделирование, основанное на методе конечных элементов, остается одним из базисных подходов для симуляции роста повреждений [8-18]. Наряду с хорошо разработанными и апробированными подхода- ми, предлагаются и развиваются принципиально новые приемы вычислений [8; 9]. Например, в [8] предложена усовершенствованная перидинамическая модель для моделирования вязкоупругой деформации и повреждений при ползучести. Ключевые элементы предлагаемой формулировки включают в себя перидинамические конституциональные уравнения зависящей от времени определяющей модели и неявную дискретизацию пери-динамических уравнений. Перидинамическое моделирование деформации ползучести и повреждений, в котором векторы плотности сил в уравнениях равновесия перидинамики (ПД) получены путем рассмотрения модели ползучести Лю и Мураками с параметром повреждения, выполнено в [9]. Градиент деформации определяется с помощью дифференциального оператора перидинамики. Граничные условия сцепления и перемещения непосредственно задаются с помощью новой стратегии при решении уравнений равновесия ПД. ПД-форма элементов сцепления позволяет создавать условия сцепления в реальной области «пограничного слоя» без каких-либо нефизических перегибов вблизи границ. Этот подход был проверен для случаев одноосного и двухосного нагружений с учетом деформации ползучести, вызванной постоянными напряжениями при высоких температурах. Авторы показывают [9], что предсказания деформации при ползучести находятся в отличном согласии с экспериментальными данными и аналитическими решениями.

Франкфорт и Мариго [10] усовершенствовали энергетическую теорию разрушения и предложили вариационную модель линейного упругого разрушения, которая разлагает общую энергию конструкции на сумму энергии деформации при деформировании и энергии разрушения при распространении трещины. В ней утверждается, что ранее существовавшие трещины и дефекты в материале будут расширяться под воздействием внешних нагрузок, что приведет к снижению общей энергии системы. На основе этой модели было разработано дополнительное скалярное фазовое поле, вводимое для описания процесса эволюции повреждений в материале через его вариации, что позволило сформировать основу метода фазового поля разрушения (МФП). Реализация дискретного расчета МФП обычно основана на МКЭ, но процесс генерации сетки в традиционном МКЭ является громоздким и часто использует полигональные сетки для дискретизации геометрических структур [11]. Это неизбежно приводит к геометрическим ошибкам, которые снижают точность расчетов напряжений и деформаций при обработке сложных траекторий трещин и детальных геометрических характеристик. Изогеометрический анализ напрямую использует геометрические модели автоматизированного проектирования для анализа и вычислений и позволяет избежать внесения геометрических ошибок и обеспечивая более точное геометрическое представление. Кроме того, МФП может легко удовлетворить требования к непрерывности более высокого порядка, что делает его весьма подходящим для моделирования тонких вариаций геометрии и сложных структур. Исследование [12] обеспечивает формирование и расчетно-экспериментальное обоснование подхода для прогнозирования живучести и долговечности элементов конструкций, базирующегося на принципах допустимой поврежденности и имитационного моделирования. Авторы [12] дополнительно отмечают, что подходы и методы, используемые в исследовании, тесно взаимосвязаны и в значительной степени дополняют друг друга. Несомненной инновационной новизной результатов является комплексный подход к оценке целостности конструкции, который сочетает в себе формулировку определяющих уравнений с функциями повреждения, численное моделирование на основе МКЭ и метода фазового поля разрушения, экспериментальные исследования усталости и роста трещин с прямыми измерениями полей деформаций с использованием метода DIC. Авторы [12] еще раз показывают, что численное моделирование имеет особое значение для практического применения, поскольку устраняет недостатки натурных испытаний конструкций, которые не обладают необходимой статистической надежностью и ограничены для прямых измерений процессов накопления и роста повреждений в процессе эксплуатации.

Одним из быстро развивающихся направлений исследований является учет особенностей совместного влияния циклического нагружения и накопления деформаций ползучести [13; 14]. В [13] предложена модель накопления усталостных повреждений на третьей стадии ползучести, учитывающая и описывающая двустороннее влияние усталостных повреждений и повреждений, аккумулируемых при ползучести в элементах конструкций, работающих в режимах периодического (циклического) нагружения при повышенных температурах. Экспериментально-численная модель на основе выбранного эволюционного закона накопления повреждений Лангеберга [13] при ползучести, скомбинированной с усталостными повреждениями, применена для прогнозирования срока службы однонаправленных ламинатов с произвольными углами ориентации [13]. Следовательно, модель, развитая в [13], учитывает 1) воздействие температуры на прирост поврежденности при ползучести и 2) аккрецию повреждений при ползучести в различных условиях действия циклических нагрузок при повышенных температурах (т.е. при одновременном протекании процессов усталости и ползучести). Обзор современных вычислительных подходов может быть найден в [15], где детально описаны применяемые в самое последнее время численные методы механики разрушения и поврежденности. В этой работе представлено введение в популярные вычислительные модели механики повреждений и механики трещин, а также основные достижения и современное состояние применения вычислительных технологий в инженерии. Однако, несмотря на новейшие вычислительные подходы, обеспечивающие точное численное описание про- цессов деформирования и разрушения, занявшие доминирующее положение в исследованиях явлениях разрушения на различных масштабных уровнях, классический метод конечных элементов позволяет пролить свет на структуру аналитических решений задач механики разрушения и поврежденности.

В настоящей работе для моделирования и анализа процессов накопления поврежденности применяется пользовательская процедура UMAT конечноэлементного комплекса SIMULIA Abaqus [16–20], встраивающая кинетическое уравнение накопления повреждений и степенной закон ползучести, соединяющий скорость деформации ползучести с истинными напряжениями в деформируемом теле, в вычислительный сценарий МКЭ, что дает возможность численно рассмотреть и оценить два обоюдных процесса: 1) развитие поврежденности и эффекты его влияния на напряженно-деформированное состояние и 2) воздействие эволюции напряженно-деформированного состояния в условиях ползучести на рост повреждений в материале. В целом идея внедрения пользовательских процедур в вычислительную реализацию МКЭ не нова и активно применяется для расчета поля поврежденно-сти у концентраторов напряжений [16–20]. В отличие от подходов, осуществленных в [16–20] и предыдущих работах авторов [21–25], ниже, на основании КЭ-подхода с применением пользовательской утилиты UMAT, выявлен автомодельный характер процесса накопления повреждений. Опираясь на полученное МКЭ-решение, нам удалось обнаружить диапазоны изменения расстояния от вершины дефекта и временные интервалы, на которых справедливо автомодельное представление решения задачи о накоплении повре-жденности у вершины трещины в условиях ползучести, подчиняющемся степенному эволюционному уравнению для среды со степенными конституциональными соотношениями.

Компьютерная симуляция процессов аккумуляции повреждений

Процессы накопления повреждений в материале существенно влияют на прочностные характеристики изделия, его ресурс и характер разрушения [1–7]. Чтобы воспроизвести механизмы накопления повреждаемости в условиях высокотемпературной ползучести на стадии проектирования изделия, требуются математические модели аккумуляции повреждений. Континуальная теория поврежденности является популярным и эффективным подходом к описанию накопления повреждений в условиях ползучести материала [27–31]. Несмотря на то что многие коммерческие МКЭ-пакеты имеют значительное количество встроенных моделей материалов, которые могут быть использованы в расчетах, они все еще немного отстают от достижений в области технологий материаловедения. Но благодаря расширенным возможностям такого программного продукта, как

Simulia Abaqus, а именно использование пользовательских процедур, все же существует способ учета в расчетах требуемого поведения материала, включая процессы накопления в нем повреждений.

Пользовательские процедуры, или подпрограммы UMAT, представляют собой программный код языка Fortran, описывающий поведение материала. Совместимость созданной пользователем подпрограммы UMAT с остальными библиотеками программного комплекса осуществляется с помощью определения входных и выходных данных. В зависимости от задачи к таким данным можно отнести механические и физические свойства материала (модуль Юнга, коэффициента Пуассона, плотность и т.д.), компоненты тензора напряжений и деформаций, его упругую и пластическую составляющие и др. Полная информация о создании пользовательских процедур приведена в руководстве программного продукта Simulia Abaqus [26]. Таким образом, Abaqus UMATs – это подпрограммы в кодировке Fortran, которые вычисляют определяющие уравнения на каждой итерации. Входные данные для задачи механики включают в себя значения приращения деформации (DSTRAN), суммарные значения деформации в конце предыдущего приращения (STRAN), напряжения при предыдущем значении приращения напряжения и свойства материала (PROPS). Приращения времени определяются в переменной DTIME вместе с текущим значением времени (TIME), а набор переменных состояния передается в виде вектора в STATEV. После вычисления определяющих уравнений ключевыми выходными данными в конце приращения времени являются обновленный вектор напряжений STRESS, согласованная матрица DDSDDE и обновленный вектор переменных состояния STATEV.

В настоящей работе реализовано включение модели Качанова – Работнова, являющейся, с одной стороны, пионерской работой [30; 31] и, с другой стороны, широко используемой в самое последнее время [27–29], в численные алгоритмы МКЭ с помощью пользовательской утилиты UMAT. Исследование полученного многопараметрического МКЭ-решения (вычислений для различных материалов с разными показателями степеней кинетического и определяющего уравнений) и проведенный анализ характера временного поведения напряжений и сплошности вблизи вершины разреза позволили идентифицировать отрезки изменения радиальной координаты и временные интервалы, для которых имеет место автомодельный характер распределения напряжений и поврежденности. В методических целях в следующем параграфе приводятся основные уравнения задачи, анализ размерностей величин, входящих в математическую постановку задачи, и вывод автомодельного представления задачи. В четвертом параграфе приводятся результаты МКЭ-анализа решения задачи об одноосном растяжении пластины с центральным разрезом в условиях ползучести.

Основополагающие соотношения.Анализ размерностей и автомодельное представление решения

лизу размерностей величин [36-38] и переходят к следующим безразмерным переменным:

° kl =° kl / ° B , ^£ kl = ^£ kl / ^£ B , t = t / T , r = r / L , V = V , ⁽⁴⁾

Для установления и последующего анализа распределений поврежденности и напряжений вблизи кончика разреза в растягиваемой по нормали к плоскости разреза пластине на стадии установившейся ползучести с учетом аугментации повреждений была избрана ключевая модель КР [30; 31]. Поведение материала под нагрузкой задается конституциональными соотношениями, сформулированными на основе апробированного и вошедшего в вычислительную практику степенного закона Бейли-Нортона:

где ° _B - некоторое характерное значение напряжения, £ _B - некоторое характерное значение скорости деформации ползучести, L - некоторая характерная длина, T - характерное время. Введение безразмерных величин (4) соотношения (1)-(3) принимают вид:

3 £„£„ = - B °'

B kl 2 ^j

n

Л \ n -1

° e

L v J

Л skl

,

V

£

- 3 «I Я е kl Bⁿ I

2 IV

n - 1

s_kl ,

V

° B ° и

^

I C *

х 1/( n + 1)

Л

BI n Lr

° kl ⁽ ф , ⁿ ),

где £ _kl - компоненты тензора скоростей деформаций ползучести; V — параметр сплошности Качанова; s_kl = ° ki — ° pp $ ki /3 - компоненты тензора девиатора напряжений; ° _kl - компоненты напряжения; ° _е = у] 3 s _kl s _ki / 2 - интенсивность касательных напряжений (второй инвариант тензора напряжений); B , n -постоянные материала, значения которых для современных металлов и сплавов могут быть найдены в [32]. Граничное условие в бесконечно удаленной точке ( r ^ и ) представляет собой условие асимптотического сближения с решением Хатчинсона, Райса и Розенгрена (HRR-асимптотикой) [33-35] (с использованием аналогии Хоффа): при условии отсутствия процесса развития повреждений ( V = 1) для всех n >  1 справедливо следующее представление

d V

dt

d V 1

Л _ dt T

- A ° ^m B

° е

L v J

.

Следовательно, масштаб £ _B может быть выражен через ° _B посредством равенства: £ _B = B ° _B , где в силу (5) масштаб ° _B определяется через характерную длину L :

° b = ( C * / ( BI n L )f n ^{+ 1)}.                 (6)

Введенный временной масштаб T , согласно (5), удовлетворяет соотношению:

I C * х 1/( n + 1)_

° kl ⁽ r , Ф , t ) ^ I I       ° kl ⁽ Ф , n )^,

I ^BI n r J

где С * - не зависящий от пути инвариантый интеграл теории установившейся ползучести [33-35]; I n ( n ) -функция, зависящая от n и определяемая как безразмерный С * -интеграл; ° ki ( ф , n ) - безразмерные функции, зависящие от полярного угла ф и показателя нелинейности материала определяемые решением Хатчинсона, Райса и Розенгрена [33-35], r - расстояние от вершины разреза, t - время. Кинетическое уравнение имеет вид:

1/ T = A ° B ,                    (7)

которое с учетом (6) приобретает вид:

m /( n + 1)

C / ( BI _n L ) )       .          (8)

В соответствии с вышеприведенным анализом размерностей величин безразмерные напряжения ° _kl как функции от введенных безразмерных переменных допускают представление:

° kl = ² kl ( ^r / ^L , t / T , Ф , ⁿ , ^m ) =

/            / * /        \\^m /( n + 1)            \           ⁽⁹⁾

= 2_и ( r / L , tA ( C * / ( B^L ) )       , ф , n , m ) .

d v = A \°l dt L V

где A, m - постоянные кинетического уравнения, определяемые экспериментально. Для выяснения возможности введения автомодельной переменной и автомодельного представления решения обращаются к ана-

Решение (9) не должно зависеть от неизвестного характерного линейного размера L , отсутствующего в постановке задаче. Иначе, можно сказать, принимается предположение, что характерный размер тела много больше длины трещины, т.е. этот параметр стремится к бесконечности, и мы приходим к вырожденной постановке задачи и параметр характерная длина L исключается путем введения автомодельной переменной R [36-38]:

R = r /

n + 1

k ( n ) ( At ) m

k ( n ) = C * / ( Bi n ) . (10)

Тогда справедливо автомодельное представление напряжений

° kl ( r , ф , t ) = 6 kl V B = ( At )^{- 1} / m ^S ki ( R , ф ) .       (11)

Граничные условия при r ^® также могут быть сформулированы в обобщающей соотношения (2) форме:

a ki ( r , ф , t ) ^ Cr s С у ( ф , n ).              (12)

С учетом введенных безразмерных параметров соотношение (12) приобретает вид:

с kl ( r , ф , t ) = с B S kl ( r / L , t / T , ф ) = Ck t a ^ ( R , ф ). (13) где автомодельная радиальная переменная определяется выражением

m -|1/(sm)                m \-1/(sm)                 m X -1/(sm)

R = r\tAC I , k = (AC I , k = (AC ) .(14)

В результате получено автомодельное решение, обладающее структурой:

^a kl (^r, ф , t ) = ( At )^{- 1} / m ^S kl ( ^R , ф ) , _m 1/( sm )         (15)

ф ( r , ф , t ) = T ( R , ф ) , R = r I tAC I .

В (15) S _kl ( R , ф ) и T ( R , ф ) - безразмерные функции от двух безразмерных величин R , ф . Эти функции подлежат определению при решении задач с конкретными граничными условиями.

Вычислительная процедура и результаты

Для численного нахождения и анализа образования, роста и слияния повреждений вблизи вершины разреза в режиме ползучести развита программа UMAT, моделирующая степенные соотношения (1) и (3) в КЭ-вычислениях. Для выполнения КЭ-расчета с созданной пользовательской подпрограммой необходимо идентифицировать ее в SIMULIA Abaqus в расчетной задаче. Для этого создается материал через меню программного комплекса SIMULIA Abaqus Materials дерева проекта. Постоянные материалы задаются в меню Mechanical Constants. В коде UMAT они описаны в меню ELASTIC PROPERTIES. Во время расчета UMAT вызывается для каждой материальной точки на каждой итерации расчетного временного шага. В рамках вычислительного эксперимента проведено компьютерное КЭ-моделирование одноосного нагружения пластины с центральным разрезом. КЭ-модель пластины имеет размеры 0,1×0,1м. Трещина моделируется разрезом с закругленными вершинами, длина и радиус которых составляют соответственно 10 ^{- 2} м и 10 - 6 м (рис. 1).

КЭ-модель пластины выполнена преимущественно квадратными элементами первого порядка, т.е. элементами, не имеющими промежуточных (срединных) уз- лов. У вершины трещины в исследуемой зоне сетка структурированная, количество конечных элементов, характерный размер которых равен 2 -10-4 мм, на четверть окружности у закругления выреза равно 18. Построение геометрии модели и КЭ-сетки осуществлялось с максимальным измельчением сетки, исходя из возможностей программного комплекса SIMULIA Abaqus. Вид сетки у вершины дефекта представлен на рис. 2.

Рис.1. Геометрическое представление пластины с закругленным вырезом в МКЭ-пакете

Fig. 1. Geometry of a plate model with a rounded crack in the FEM platform

Рис. 2. КЭ-сетка: типичный пример КЭ-разбиения вблизи закругленного выреза

Fig. 2. FEM mesh: standard example of FEM: the structured grid near the rounded notch

Для расчетов были выбраны материалы со значениями материальных констант B и n согласно данным таблицы.

Материальные постоянные

Material constants

n	m	B , (Н/мм 2 ) -n (ч) -1	Модуль Юнга, МПа	Коэффициент Пуассона
5	3,5	2.2 10 -17	121000	0,34
7	4,9	1.9 10 -22	121000	0,34
9	6,9	1.6 10 -27	121000	0,34

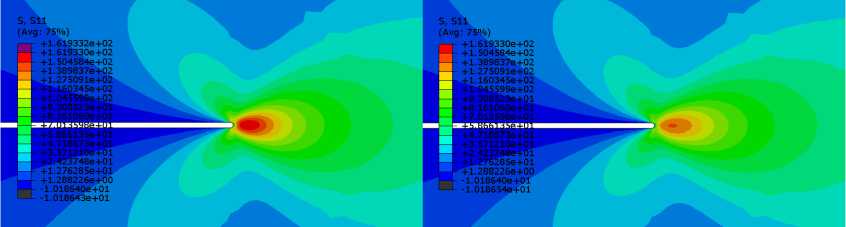
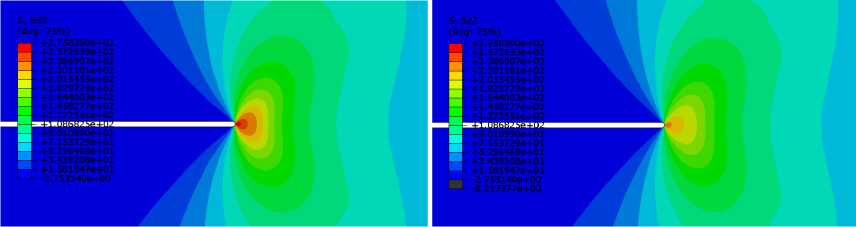
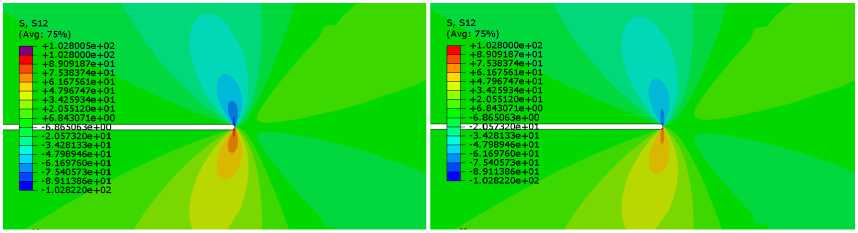
Валидация результатов, полученных для данной модели, проводилась с помощью сравнения с известным аналитическим решением Хатчинсона – Райса – Розенгрена [33–35]. Хорошая сходимость позволила использовать данную КЭМ для дальнейшего исследования. Для большого ряда значений материальных постоянных кинетического уравнения (3) и конститу- циональных уравнений (1) найдены механические поля вблизи закругленного кончика разреза. На рис. 3 представлены результаты расчета с показателем ползучести n = 7 и двух моментов времени: 4000 и 10000 ч, а также приведено распределение полей напряжений.

Распределение интенсивности деформаций ползучести представлено на рис. 4.

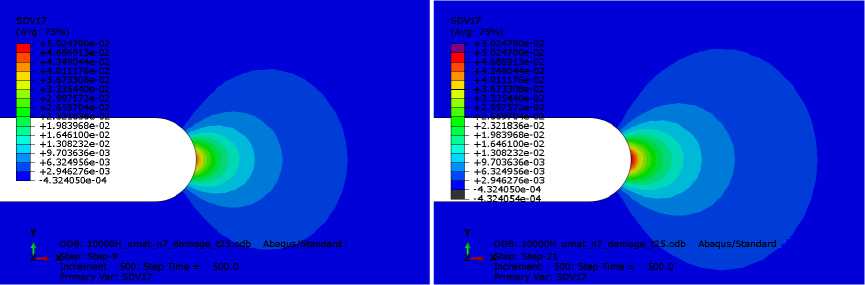
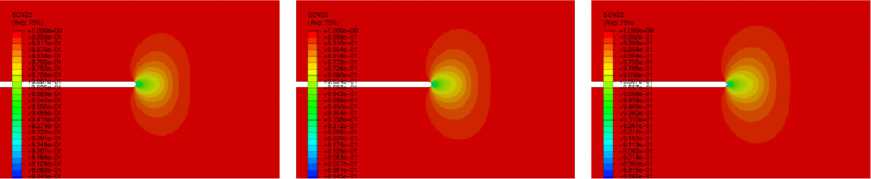
На рис. 5 изображены картины распределений параметра сплошности (линии равных значений сплошности) для значения показателя степени определяющих соотношений n = 7 с течением времени.

b

c                                                 d

f

e

g

h

Рис. 3. Распределение поля напряжений: a – интенсивность напряжений, 4000 ч; b – интенсивность напряжений, 10000 ч; c - компонента 3 11 , 4000 ч; d - компонента 3 11 , 10000 ч; e - компонента <3 22 , 4000 ч; f - компонента 3 22 , 10000 ч;

g - компонента 3 12 ,4000 ч; h -компонента 3 12 ,10000 ч

Fig. 3. Stress field distribution: a – stress intensity, 4000 h; b – stress intensity, 10000 h; c – component, 4000 h; d – component, 10000 h; e – component, 4000 h; f – component, 10000 h; g – component, 4000 h; h – component, 10000 h

а

b

Рис.4. Распределение интенсивности деформаций ползучести для 4000 ч ( а ) и 10000 ч ( b )

Fig. 4. Equivalent creep strain distributions for 4000 h ( a ) and 10000 h ( b )

a                                  b                                c

d

g

Рис. 5. Распределение параметра сплошности у вершины трещины: a – 500 ч; b – 2000 ч; c – 4000 ч; d – 6000 ч; e – 8000 ч; g –10000 ч

Fig. 5. Distribution of the continuity parameter at the crack tip: a – 500 h; b – 2000 h; c – 4000 h; d – 6000 h;

e – 8000 h; g –10000 h

Для показателей ползучести n = 5 и n = 9 были получены аналогичные картины.

Извлеченные из численных КЭ-результатов распределения компоненты тензора напряжений а22 вдоль линии продолжения разреза, соответствующей радиальной траектории ф = 0 , отображены на рис. 6 в двойных логарифмических координатах для различных значений времени для n = 5, n = 7 и n = 9. Анализируя полученные кривые, можно сделать вывод, что в КЭ-расчетах с принятием во внимание процесса накопления повреждений в зоне ползучести наблюдается выход на асимптотическое поведение напряжений: прямые красные линии на графиках (см. рис. 6), аппроксимирующие значения компоненты тензора напряжений а22 для указанных моментов времени. На рис. 6 все кривые совпадают для упругого участка деформирования (см. рис. 6, слева на каждой иллюстрации). На рис. 6 справа показано, что все кривые в области развитой ползучести имеют одинаковый наклон, что отвечает выходу на степенную асимптотику.

Полученные из численного расчета средние значения коэффициента наклона этих прямых равны: для n = 5 значение коэффициента наклона l = -s = 0,4 ; для n = 7 значение коэффициента наклона l = -s = -0,33; для n = 9 значение коэффициента наклона l = -s = 0,3. Ранее было показано [39; 40], что уравнения задачи (1)– (3) допускают автомодельное представление решения (15) с промежуточной автомодельной переменной (14), где показатель степени s находится из решения краевой задачи. Поэтому дальнейший анализ КЭ-решения был нацелен на определение показателя степени s , а также интервалов изменения радиальной и временной координат, для которых справедливо представление (14). На рис. 7–9 изображены кривые зависимости компоненты напряжения а22 (r, ф = 0) (отнесенного к приложенной растягивающей нагрузке) от автомодельной переменной, показанные в двойных логарифмиче- ских координатах. В автомодельных координатах m 1/(sm)

П22 = с22(r,ф = 0,t)(At) m иПR = R = rI tAC I все расчетные точки ложатся на единую кривую П 22 =П22(R, ф = 0).

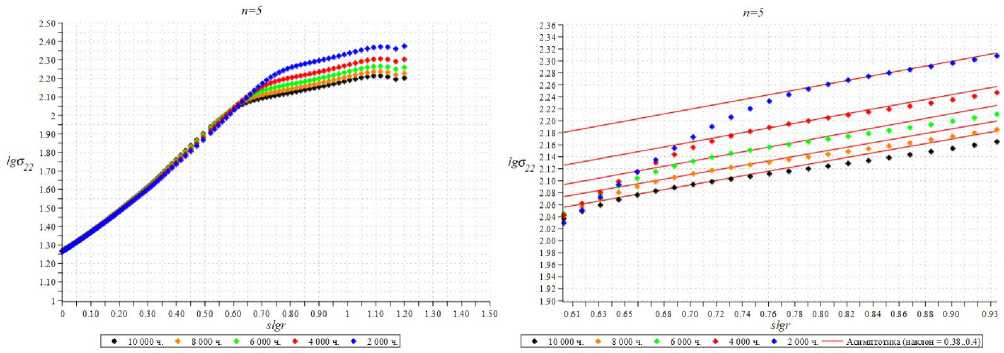
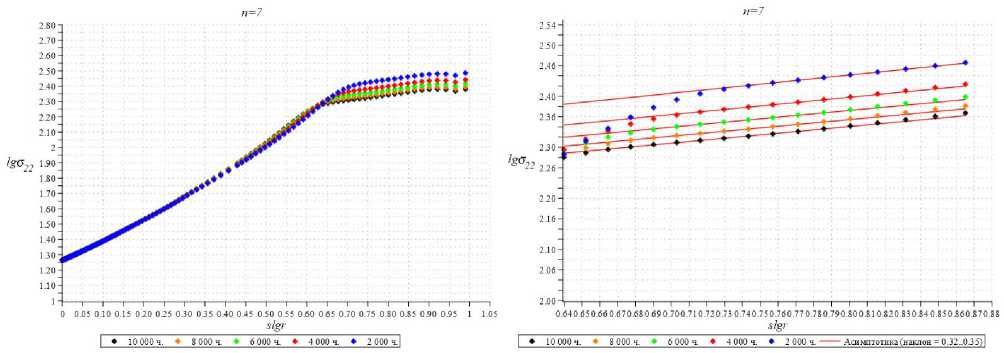
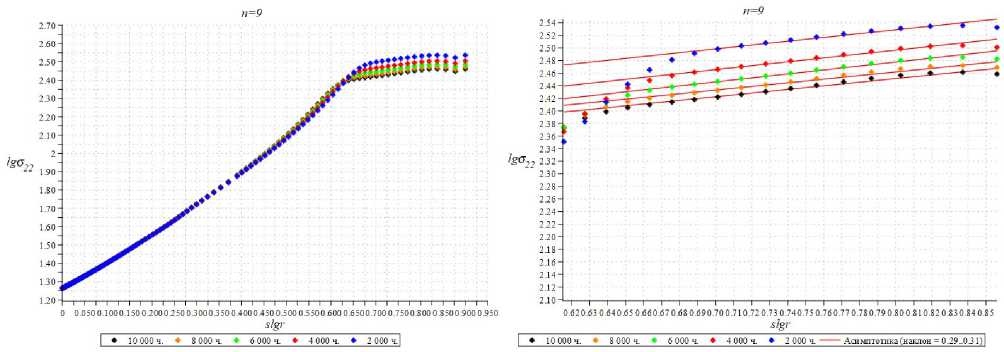
Рис. 6. Распределение компоненты тензора напряжений G 22 у вершины трещины

Fig. 6. Distribution of the stress tensor component a ₂₂ at the crack tip

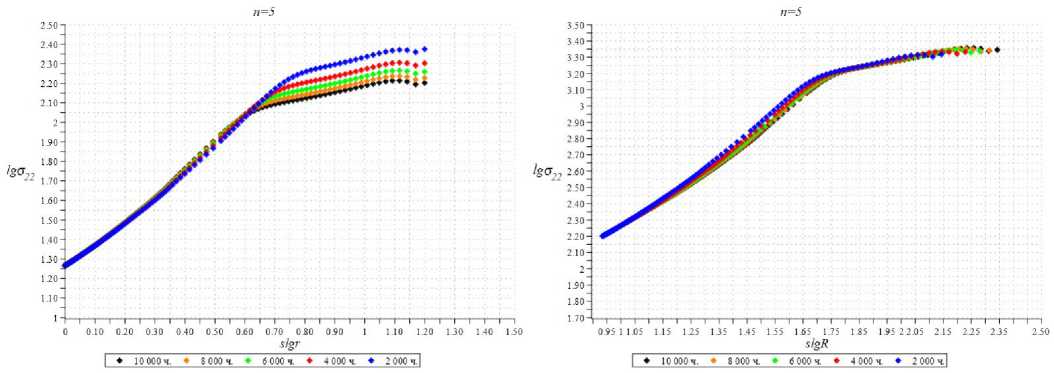
Рис. 7. Нормальная компонента тензора напряжений а ₂₂ как функция расстояния от кончика разреза для показателя ползучести n = 5 в двойных логарифмических координатах: кривые зависимости безразмерного напряжения а ₂₂ ( r , ф = 0) (отнесенного к приложенной нагрузке) от расстояния от кончика разреза r для различных времен (слева) и кривая зависимости безразмерного напряжения С ₂₂ ( R , ф = 0 ) (нормированного в соответствии с формулами (14)) от автомодельной переменной R (справа)

Fig. 7. Normal components of the stress tensor a ₂₂ as a function of the distance from the crack tip for the creep index n = 5 in log-log coordinates: curves of dependence of the dimensionless stress a ₂₂ ( r , ф = 0) (related to the applied load) on the distance from the crack tip r for different times (left) and the curve of dependence of the dimensionless stress a ₂₂ ( R , ф = 0 ) normalized according to the eqn.(14) on the self-similar variable R (the scaled coordinates in accordance with eqn. (14)), (right)

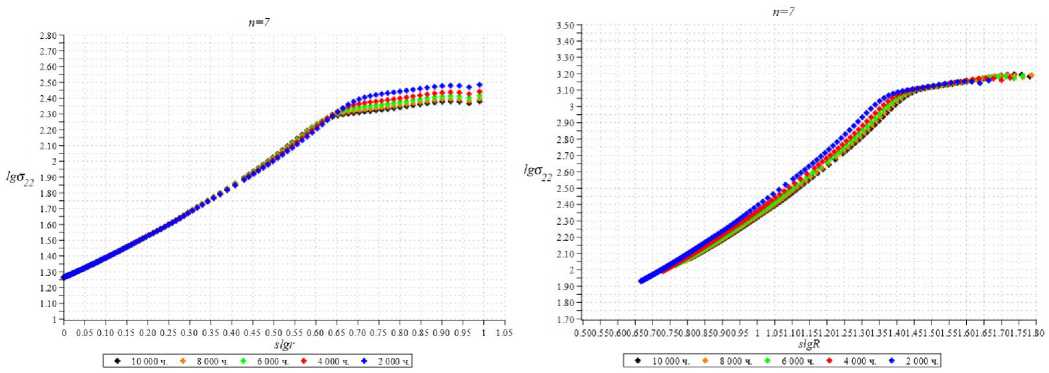
Рис. 8. Нормальная компонента тензора напряжений а ₂₂ как функция расстояния от кончика разреза для показателя ползучести n = 7 в двойных логарифмических координатах: кривые зависимости безразмерного напряжения а ₂₂( r , ф = 0) (отнесенного к приложенной нагрузке) от расстояния от кончика разреза r для различных времен (слева) и кривая зависимости безразмерного напряжения а ₂₂ ( R , ф = 0 ) (нормированного в соответствии с формулами (14)) от автомодельной переменной R (справа)

Fig. 8. Normal components of stress tensor a ₂₂ as a function of the distance from the crack tip for the creep index n = 7 in log-log coordinates: curves of dependence of the dimensionless stress a ₂₂ ( r , ф = 0) (related to the applied load) on the distance from the crack tip r for different times (left) and the curve of dependence of the dimensionless stress a ₂₂ ( R , ф = 0 ) normalized according to the eqn.(14) on the self-similar variable R (the scaled coordinates in accordance with eqn. (14)), (right)

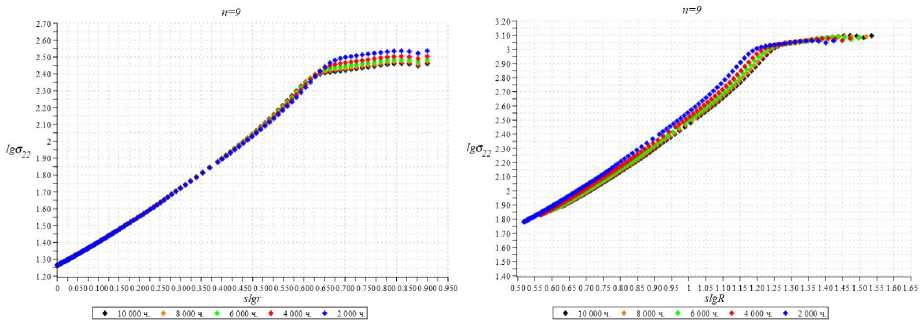
Рис. 9. Нормальная компонента тензора напряжений <522 как функция расстояния от кончика разреза для показателя ползучести n = 9 в двойных логарифмических координатах: кривые зависимости безразмерного напряжения 5 22 ( r , ф = 0) (отнесенного к приложенной нагрузке) от расстояния от кончика разреза r для различных времен (слева) и кривая зависимости безразмерного напряжения 5 22 ( R , ф = 0 ) (нормированного в соответствии с формулами (14)) от автомодельной переменной R (справа)

Fig. 9. Normal components of the stress tensor 6 22 as a function of the distance from the crack tip for the creep index n = 9 in log-log coordinates: curves of dependence of the dimensionless stress 6 22 ( r , ф = 0) (related to the applied load) on the distance from the crack tip r for different times (left) and the curve of dependence of the dimensionless stress 6 22 ( R , ф = 0 ) normalized according to the eqn.(14) on the self-similar variable R (the scaled coordinates in accordance with eqn. (14)), (right)

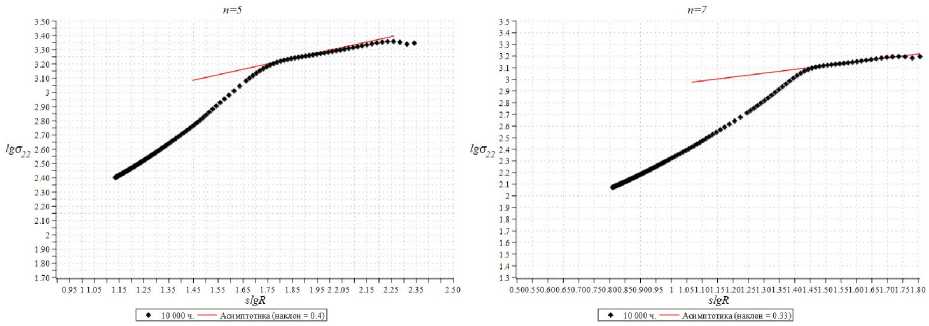
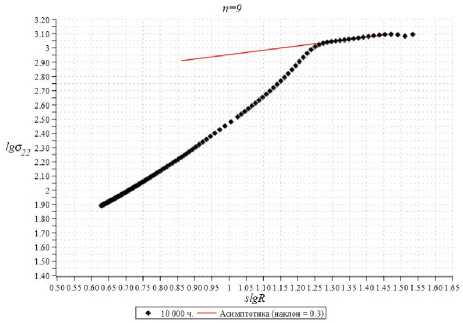
Рис. 10. Кривые зависимости безразмерного напряжения 6 22 от автомодельной радиальной координаты R .

Асимптотика в зоне ползучести

Fig. 10. Curve of dependence of the dimensionless stress 6 22 on the self-similar radial coordinate R .

Asymptotics in the creep zone

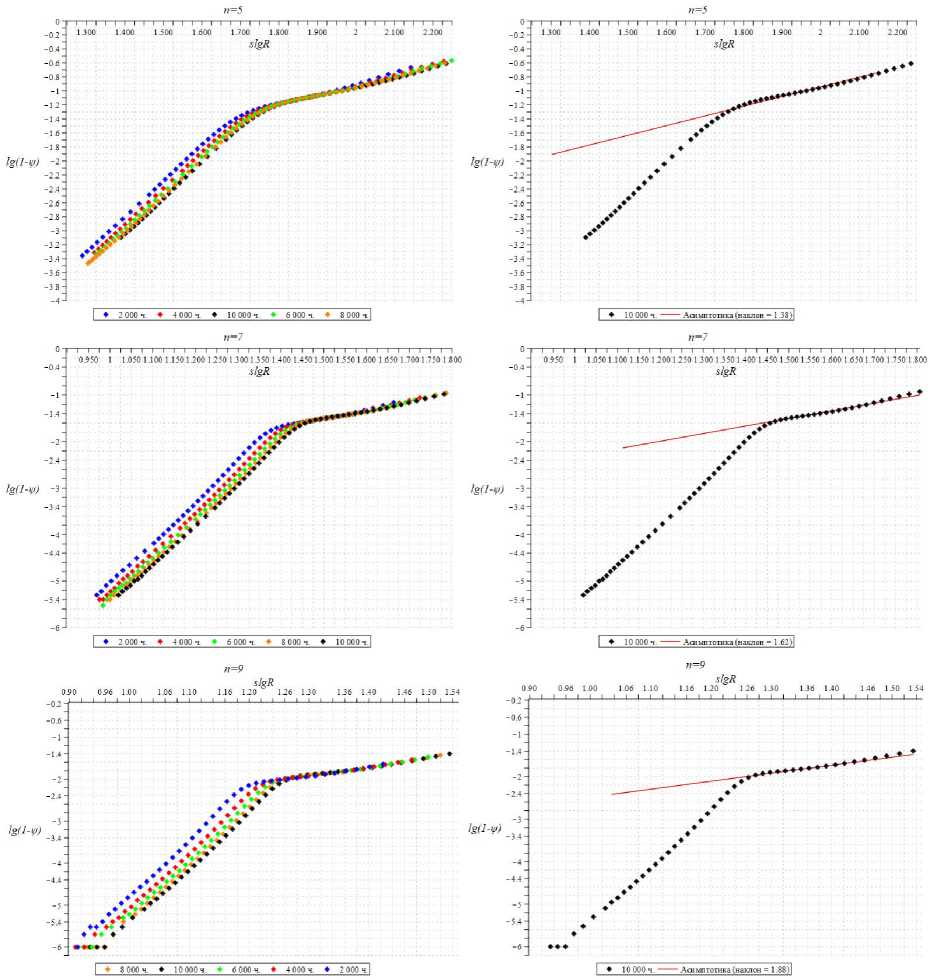
Рис. 11. Кривые зависимости параметра поврежденности 1 - у от автомодельной переменной R . Асимптотика в зоне ползучести

Fig.11. Curve of dependence of the damage parameter 1 — у on the self-similar radial coordinate R . Asymptotics in the creep zone

Из рис. 7–9, справа, отчетливо видно, что кривые, отвечающие различным временам, объединяются в единую кривую в диапазоне автомодельной переменной, отвечающем временам и расстояниям от кончика трещины, для которых развивается ползучесть и процесс накопления повреждений, что ясно свидетельствует об автомодельном характере распределения напряжений. Данное автомодельное решение можно интерпретировать как автомодельное решение второго рода, поскольку искомые степени в автомодельном представлении решения разыскиваются численно для рассмотренных в МКЭ-анализе показателей нелинейности степенного определяющего закона ползучести (1) и степенного эволюционного уравнения (3). Для случая n = 5 показатель степени приближенно равен

0,4; для n = 7: 0,33; для n = 9: 0,3. Полученные значения степеней совпадают с коэффициентами наклона кривых зависимости безразмерного напряжения а ₂₂ от автомодельной радиальной координаты в двойных логарифмических координатах (рис. 10), а также с коэффициентами наклона кривых, соответствующих распределению компонент тензора напряжений а ₂₂, представленных на рис. 6.

Полученные значения показатели степеней в автомодельном представлении решения s < 0, значит, из кинетического уравнения (3) следует, что у = 1 — Rmg (ф), lg(1 — у) = sm lg R + lg g (ф), (16)

где m = 0,7 n .

Кривые зависимости параметра поврежденности 1 - у от автомодельной промежуточной переменной R (при ф = 0), изображенные в двойных логарифмических координатах, приведены на рис. 11, на которых определенно видно, что кривые, отвечающие различным моментам временам, также объединяются в единую кривую  (совпадают)  в зоне  ползучести.

В автомодельных координатах Пу = 1 - ф(R, ф = 0) и m 1/(sm)

ПR = R = г I tAC I все расчетные точки ложатся на единую кривую Пу = Пу (R), причем на тех же самых расстояниях, что и кривые зависимости безразмерного напряжения а22 от промежуточной автомодельной переменной (см. рис. 7–9).

Наклон этих кривых в зоне ползучести (см. рис.11) равен приближенно 1,38; 1,62; 1,88, что совпадает со значениями, получаемыми по формуле k = - sm . Для случая n = 5 : k = - sm = 0,4 ■ (5 ■ 0,7) = 1,4; при n = 7: k = - sm = 0,33 ■ (7 ■ 0,7) = 1,62; при n = 9: k = - sm = 0,3 ■ (9 ■ 0,7) = 1,89.

Заключение

На основе вычислений, проведенных с помощью пользовательской процедуры UMAT, добавляющей кинетическое степенное уравнение накопления поврежде- ний и степенной конституциональный закон с истинными напряжениями в конечно-элементный анализ, выявлено свойство автомодельности распределений напряжений и поврежденности вблизи закругленной вершины трещины в поврежденной среде в процессе ползучести. Полученные и проанализированные радиальные зависимости напряжений и сплошности позволяют выявить асимптотику дальнего и ближнего полей напряжений и сплошности. Акцент в настоящем исследовании сделан на асимптотике дальнего поля, для которого для ряда значений материальных констант даны оценки показателей степеней автомодельной промежуточной асимптотики и степеней в автомодельном представлении решения. Новизной выполненного теоретикочисленного анализа, базирующегося на МКЭ, является выделение промежуточной автомодельной структуры решения и диапазонов изменения радиальной и временных координат, для которых справедлива выделенная автомодельная структура решения.