Автомодуляция одномерных волн на основе нелинейного уравнения Шредингера с некерровской нелинейностью

Перечень физических приложений стандартного нелинейного уравнения Шредингера (НУШ) i ду / д t + д ² у / д x ² + 2 п| У² у = 0 , описывающего в общем случае эволюцию огибающей несущей ква-зимонохроматической волны в слабонелинейной системе, и связанных с ним нелинейных урав нений в настоящ ее время чрезвычайно обширен, и вряд ли мо жно сомневаться в их физической значимости. Нелинейный кубический член у² у в различных физич еских моделя х, описываемых этим уравнением, возникает об ычно из степенно -го разло жения некоторой физич еско й величины n_NL , зависящей от интенсивности I = у ². Это разложение имеет вид:

n NL ( I ) = П 2 1 + П 4 1 ² + .... = П 2 У + n 4 У +.....

К примеру, в нелинейной оптике n_NL - нелинейная часть показателя преломления n = n₀ + n NL . Стандартный безразмерный вид НУШ, приведенный выше, записан при учете наинизшего члена разложения n_NL = n ₂ I = n ₂ У ². При этом коэффициент нелинейности п пропорционален n₂ .

Функция нелинейного отклика системы n_NL ( I) на внешнее воздействие несущей квазимонохро-матич еско й волны в общем случ ае имеет сло жный вид, определяемый конкретным ф изическим механизмом взаимод ействия системы с по лем несущей волны . Для нахо жд ения явного вида n NL ( I ) часто требуется квантовомеханический расч ет, не позволяющий определить аналитическую зависимость функции отклика от интенсивности в широ-ком д иапазо не. Функция отклика должна об лад ать двумя очевидными свойствами, а именно: об ра-щаться в ноль при I = 0 и выходить на насыщение при I >>1. Степенное разложение, указанное выше, применимо при малых значениях интенсивно -сти, но даже в этом случ ае, если ось I является правой касательной к графику функции n_NL ( I ) в

нуле, то разло жение начинается то лько с члена n ₄ 1 ² = n ₄ У ⁴ , что приводит к НУШ

i ду / д t + д ² у / д x ² + 2 ^У| ⁴у = 0 с нелинейностью пятой степени.

Чтобы включить в решение и керровскую нелинейность третьей степени, рассмотрим более общее уравнение i ду / д t + д 2у / дx 2 + 2п|У ^'У = 0.            (1)

При v = 1 уравнение (1) очень хорошо изучено [1] и его решение имеет вид

у = A

exp

{'[ ш /2 + ( u ² - u ²) t /4 + ф ₀ ]}

u ch — (x - x0 - ut)

где u = 2 A П ■ Здесь A, u ,x ₀, ф ₀ - свободные параметры.

Основной формализм

Целью данной работы является решение уравнения (1) при произвольном v > 0 (не обязательно целом) прямым методом, основанном на теории дифференциальных уравнений в частны х производных первого порядка и теории гамильтоновых систем.

Подстановка полевой функции у вида

у = V I exp { i ( x u / 2 - 1 5 + ф ₀ ) } ,

где u , 5 , ф ₀ - свободные параметры, в (1) приводит после отделения мнимой и веществ енной частей к

двум уравнениям

д I д I _ — + u— = 0 , д t д x

2 1 ^4 д x²

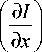
2 г 2

= a I

- 8 n I ^{v + 2},

где

a ² = u ² - 4 5 .                                 (5)

Уравнение (3) является линейным однородным уравнением первого порядка с детально разработан-

ной теорией [2]. Как известно из теории таких уравнений, общим решением (3) является любая дифференцируемая функция I = и ( 5 ( x , t ) ) , где 5 ( x , t ) - левая часть первого интеграла уравнения характеристик, имеющая, как легко проверить, вид 5 = X - X ₀ - U t .

Подстановка I = и ( 5 ) в (4) приводит к обыкновенному дифференциальному уравнению второго порядка

2 и ( 5 ) и ‘ ( 5 ) - и' ²( 5 ) = a ² и ²( 5 ) - 8^ ^{+ 2}( 5 ) . (6)

производящей функции F = 2 qArth 4 p f - q ? . Из уравнений (9) след ует явный вид преобразований:

f = 8 qch

2 p + т

1 p f = 4 th

p + т

,

а из (10) явный вид функции Гамильтона:

H = ⁽M1 ch 2( v + 1) B l! .

v + 1           2

Упрощающее масштабное преобразование 1/v f (т), Т = а5 приводит (6) к виду

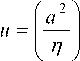
2 ff - f ² = f ² - 8 f ^{v + 2},                    (7)

На заключительном этапе совершим второе преобразование от { q , p , H } к { q , P , H = 0 } , откуда следует, что Q = con5t ; P = con5t , а производящая функция преобразования F ( p , Q, т ) удовлетворяет уравнению H ( д F / д p , p, т ) = д F / дт .

где f = df ( Т )/ d т .

Как легко проверить, (7) следует из нормальной системы гамильтоновых уравнений f = д H / д p f- , p f = -д H / д f с функцией Гамиль-

Теперь соотношения q = д F / д p , P = д F / д Q

в неявной форме задают первые интегралы гамильтоновой системы

тона

= д H / д p ; p = -д H / д q .

f 1       7 )

H=-f k -2 p f I+f k 8       7

v + 1

/( v + 1).

Уравнение для производящей фун кции с учетом (12) имеет вид

Решение уравнения (7) можно провести с помощью канонических преобразований и теории Гамильтона-Якоби. Как следует из теоремы Якоби-Пуанкаре, если существует принадлежащая классу С² функция 5 ( f , p , т ), такая, что |д² 5 / д f d p | ^ 0 , то преобразование ( f , p f ) ^ ( q , p ), генерируемое этой функцией: p f = д 5 / д f ; q = д 5 / д p , является каноническим, а новая фун кция Гамильтона имеет вид

H ( q , p , т ) = H ( f ( q , p , т ), p f ( q , p , т ), т ) +

+IS(f (q, p,т), p,т )■ дт

( 8 д F / д p )"^{+ 1} ch 2( v + 1) P + 7 = d F v + 1              2     дт

.

Покажем, что частное решение системы (14) для случая нулевых значений произвольных постоянных Q = 0, P = 0 приводит к солитонному решению исходного уравнения (1). В этом случае производящую ф ункцию можно представить в виде

F ( p , Q / т ) = g ( p , т ) + Qh ( p , т ), (16)

ограничившись первой степенью по Q , имея в виду, что после составления уравнений (13) следует положить Q = 0, P = 0 .

Подставляя (16) в (15) и удерживая только члены линейные по Q , находим

В теории канонических преобразований для двумерного фазового пространства можно исходить из четырех типов производящих функций [3]. Для дальнейших целей наиболее подходящей является

8 ^{v+ 1}

v + 1

/ X V+1              / x v

I д g I z ,J д g I д h

I — I + ( v + 1) I — I Q — k д p )          k д p ) д p

²< ^{v+ 1}) p + T ch

функция F = R ₂( p f , q, т ). Тогда явный вид преоб-

разований найдется из разрешения уравнений , дF      дF f = дpf ; p = дq ’ а новая функция Гамильтона

H(q, p, т) = H(f (q, p, т), p f (q, p, т), т)- дF (    /                                       .

(p f ⁽ q , p^{, т} )’ q , ^т )

д т

= 5g + Q ^ дт дт отсюда следуют два уравнения для g и h:

Перейдем от динамической системы { f , p f , H } к представлению взаимодействия { q , p , H } с помощью

_{v +} 1        \^{v + 1}

8     | ^{д g} |      , 2( v + 1) Р ^{+ т   д g}

1 I ch                 =     , v+ 1 kдp)            2 дт

_g v + 1 1 д g I д h ch 2( v + 1) p + т = д h k д p 7 д p 2 д т

Полагая g = g ( p + т ), из (17) находим

^д g д p

( v + l)^{1, v} - 8 1 + 1/ v     '

п - 2(1 + 1/ v ) , p + т d.

.

Подстановка этого выражения в (18) приводит к линейному однородному уравнению первого порядка dh , dh n

3--(V + 1)У = 0, дт dp простейшее нетривиальное решение которого имеет вид

у = A

h = p + (V + 1)t .

Соотношения (13) с учетом (16) дают:

dg ... dh q = 1T + QT";

d p    d p

P = h .

Полагая здесь Q = P = 0, с учетом (19) и (20), находим:

p = -(v + 1)т ,

_ (v + 1)¹ / ^V q     8 1 + 1/ v

( ch ( vt / 2) ) ^2,1" ^v ) .

Подстановка последних двух формул в (11) дает решение исходной гамильтоновой системы с гамильтонианом (8):

I. xu exp< i —

I 2

и ²

A ^{2 V} 2 n I

----A 1 1 + ^ 0

V +1 )

ch ^{1/ v}

(                        1

V A ^V -^- ( x - x 0 - u t )

4 V +1

I                       )

которое является гладкой функцией, локализованной вдоль направления x ( t ) = x 0 + u t , и представляет собой волновой пакет, движущийся без дисперсионного уширения с постоянной скоростью и . Очевидно, что при v = 1 последняя формула превращается в известное решение НУШ с кубичной нелинейностью [1].

Заключение

Таким образом, модуляция нелинейной системой (со степенным по интенсивности откликом на квази-гармоническое возмущение) несущей волны в последовательность локализованных импульсов, имеющих форму гиперболического секанса, возведенного в некоторую степень, является общей чертой НУШ с любой положительной степенью нелинейности.

/     1 A1/v f = ( ^±11   [ch(vt/2)PV;

A 8 )

P f = ^- 4 th ^{( vt /2)}

Подстановка первой из этих формул в уравнение (7) обращает его в тождество.

Из приведенного выше масштабного преобразования и первой формулы (21) получается след ующее выражение для интенсивности I :

Г 2          \1/ v

I = | « ( к + 1) 1    [ ch ( as v /2) ] ^{- 2/ V} .

I     8n    )

Учитывая (5) и вводя обозначение a ² = = 8 n A^{2 v} / ( v + 1), окончательно находим решение (2):