Автономное цифровое управление мини-спутником землеобзора в режимах начальной ориентации

После отделения любого малого низкоорбитального космического аппарата (информационного спутника [1], космического робота [2] и т.д.) от верхней ступени ракеты-носителя такой космический аппарат (КА) начинает кувыркаться – вращаться с вектором угловой скорости ω изменяемого направления в связанной с ним системе координат (ССК) O xyz . Основное назначение начальных режимов системы управления ориентацией (СУО) состоит в приведении ориентации КА к заданной в орбитальной системе координат (ОСК) O x ^o y ^o z ^o . Затем космический аппарат с помощью собственной двигательной установки перемещается в заданное положение на целевой орбите и начинает выполнять свои задачи при его удержании на этой орбите [3].

обеспечивающих непрерывное обновление видеоданных. Стоимость их разработки, а также изготовления и вывода на орбиту невелика, что объясняет превращение таких спутников в массовый продукт для ДЗЗ, а также для быстрой практической проверки новых космических технологий. Широкое использование малых спутников землеобзора стало также стимулом развития инновационных технологий, направленных на совершенствование их бортовых систем и целевой аппаратуры.

В данной статье рассматривается миниспутник землеобзора (рис. 1) массой 250 кг, оснащенный телескопом с апертурой 0.4 м, который отделяется от верхней ступени ракеты-носителя на солнечно-синхронной орбите высотой 600 км. Предполагается, что такой миниатюрный КА оснащён системой управления движением,

Рис. 1. Мини-спутник землеобзора

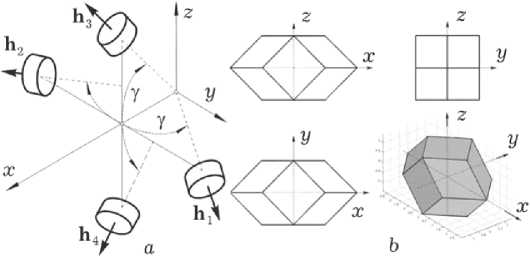
Рис. 2. Схема GE ( a ) и оболочка ее КМ ( b )

содержащей бесплатфрменную инерциальную навигационную систему (БИНС) с коррекцией по сигналам спутников GPS/ГЛОНАСС и звездных датчиков, кластер гироскопических датчиков угловой скорости (ДУС), трехосный магнитометр (MM), а также следующие бортовые приводы: двигательная установка (ДУ), кластер четырех двигателей-маховиков (ДМ) по схеме General Electric ( GE ), рис. 2, и магнитный привод (МП). Мы изучаем нелинейные проблемы управления КА в следующих режимах начальной ориентации (РНО):

• (i)    успокоение вращательного движения КА в инерциальной системе координат (ИСК) с помощью цифрового управления МП по сигналам кластера ДУС когда модуль вектора угловой скорости to = | to | > го j при заданном значении го ,;

• (ii)    инициализация кластера ДМ, включение его в контур управления КА и последующее приведение КА по сигналам БИНС к требуемой ориентации в ОСК;

• (iii)    угловая стабилизация КА в ОСК при автономном цифровом управлении кластером ДМ, в том числе при его разгрузке от накопленного кинетического момента (КМ) с использованием МП, для подготовки СУО спутника к полётной верификации её работоспособности.

Методы решения таких задач без использования каких-либо ДУ ранее были представлены в [4]. Недостатками этих разработанных методов являются необходимость временной программы пространственного наведения КА с использованием прогноза терминальных граничных условий и большая длительность приведения углового положения спутника к требуемой ориентации в ОСК.

В отличие от такого подхода, здесь в развитие [5] решается задача автономного углового наведения КА при отслеживании значений вектора модифицированных параметров Родри-га (МПР) эталонной модели с использованием модульно ограниченного вектора цифрового управляющего момента кластера ДМ в процессе приведения ориентации спутника из произвольной в ИСК к требуемой в орбитальной системе координат. Мы также кратко обсуждаем проблемы проверки работоспособности СУО в режимах начальной ориентации.

МОДЕЛИ И ПОСТАНОВКА ЗАДАЧИ

Минимально-избыточная схема GE класте- ра ДМ, рис. 2, обладает возможностью управлять ориентацией КА при отказе любого одного маховика. Здесь в ССК Oxyz оси вращения четырёх ДМ располагаются на поверхности конуса с углом полу-раствора у. Далее используются стандартные обозначения {•} = с°10,

[ • ] = line(/) , • , ) , ( • ) , [ х ] и ° ,~ для векторов,

матриц и кватернионов, С _Y = cos у , S _Y = sin у , 7—123 т = 1 4- т

^,^^,-'••• m     m и применяется вектор

МПР о = {о i} = е tg(Ф /4) с традиционными обозначениями орта Эйлера e и угла Ф соб ственного поворота. Вектор ст взаимно-одно значно связан с кватернионом Л = (X 0, X), Х = {X i} ориентации КА в ИСК прямыми О = Х/(1+ Х0) и обратными X0 = (1 -О2)/(1 + О2), X = {Xi} = 2о /(1 + О2) соотношениями.

Модель углового движения КА учитывает упругость его конструкции и имеет вид

Л = Л ° го/2 ; A ° {со , q , Q } = { F ^to , F ^q , F r } , (1)

F ^го=- [ _ю x ] G + M ^m + M ^d ;

F ^q = - A q ( V _q q + W q q ) ; F r = m - m f ;

A °

A Y

J   D q   J r A Y

D ‘    A ^q 0

q

J r A Y    0    J r 1 4

c c c

Y Y Y

S Y   - S Y    0

0    0     S Y

^C Y 0 - S _Y

Здесь G = G ° + Dqq является вектором КМ электромеханической системы, где G ° = К + Н и K = Jro, столбцы Н = {Н i}, i = 1 ^ 3 и h = {h p }, h p = JrQ p, p = 1 ^ 4 представляют КМ кластера и отдельных ДМ, которые связаны соотношением Н = AY h, где матрица AY составлена из ортов осей ДМ в базисе B ;

A q = diag{цД; V _е = diag{jQ s }

W q = diag{( Q s )²}; M ^m = { m “ }; m = { m p }; m ^f = { m p };

вектор механического момента МП M ^m = { m ™ } = - L x B , где вектор электромагнитного момента (ЭММ) L = { l i } с ограниченными компонентами | l i | < l ^m и вектор индукции магнитного поля Земли B = b B с ортом b определены в ССК ; векторы-столбцы m = { m p } и m ^f = { m p } представляют управляющие моменты и моменты сил сухого трения по осям вращения ДМ, а вектор M ^d - внешние возмущающие моменты. Ресурсы каждого ДМ по управляющему и кинетическому моментам ограничены, | m p ( t )| < m ^m ,| h _p ( t )| < h ^m , p = 1 + 4 . Далее используется вектор M ^r = {M rr } управляющего момента кластера ДМ в виде M ^г = - Н , где ( • ) * – символ локальной производной по времени.

Если КА считать свободным твердым телом, который управляется только кластером ДМ, и СУО сбалансирована по вектору суммарного кинетического момента (вектор G ≡ 0 ), то модель (1) пространственного углового движения КА принимает вид

Л = Л ° о / 2 ; о = J ^{- 1} М ^г = е = и .     (2)

Пусть для формирования управления u применяются измерения кватерниона Л(t), которые используются для вычисления вектора МПР а( t) , и вектора угловой скорости to (t). Кинематическому уравнению в (2) соответствует соотношение a = (1 — a2)to/4 + охю/2 + a(a, to)/2 для вектора МПР σ , поэтому при векторе управляющего углового ускорения u ≡ ε модель (2) представляется в нормированной непрерывной векторной форме а = ^(1 — a2)to + 2axto +1 a(a, to); to = u (3) с заданными начальными условиями О(t0) = ао , О(tо) = Оо при tо = 0, где при обозначении eо = e(to) вектор ао = eо tg(Фо/4) является произвольным с условием | Фо |< 2п.

Как известно, кватернион - Λ задает вращение КА на угол 2 п — Ф вокруг орта Эйлера - e , которое полностью совпадает с вращением этого объекта на угол Φ вокруг орта Эйлера e , т.е. значения Λ и - Λ совпадают. Следовательно, при Φ = π возникает проблема двузначности кватерниона и требуется конкретизировать его значение вместе с направлением орта Эйлера. Для вектора МПР σ такая проблема не проявляется V Ф e ( — 2 п , 2 п ) . Поэтому далее принимается эталонная модель (3)

автономного пространственного наведения с вектором МПР σ , вектором угловой скорости ω и вектором ускорения ε ≡ u , который формально считается управлением. Будем считать, что вектор такого управления u = {u i } ограничен по модулю | u ( t )| = и ( t ) < u^m , u^m >  0 , а вектор to ( t ) = { to i ( t )} ограничен по модулю | to ( t )| = to ( t ) ^m , to ^m >  0 , естественно О о = I О I ^^m -

При законе наведения КА, заданного кватернионом Л ^p ( t ) , векторами угловой скорости to ^p ( t ) и углового ускорения 8 ^p ( t ) , погрешность ориентации ССК O xyz определяется кватернионом Е = ( e ₀ , e ) = Л ^p ° Л при векторе e = {e i } , которому соответствуют матрица ошибки ориентации C ^e = I ₃ — 2[ e x ] Q ) , где матрица Q _e = I ₃ e ₀ + [ e x ] , вектор модифицированных параметров Родрига a ^e = { a e } = e /(1 + e 0 ) = e ^e tg( O ^e /4) с ортом e ^e оси Эйлера и углом ф ^e собственного поворота, а также вектор угловой погрешности 5 ^ф = ^{5ф i ^}=^{4 a ^{e }} . При этом вектор ошибки S to ( t ) = to ^e ( t ) по угловой скорости вычисляется на основе соотношения to ^e = to — C ^e to ^p ( t ) .

Предположим, что дискретное измерение кватерниона Л I - Л ( t₁ ) ориентации КА в ИСК выполняется БИНС в моменты времени t_l , 1 e N₀ ^ [0,1,2,...) периодом T_p , в моменты времени t k , k e N₀ с периодом T_u формируется цифровое управление кластером ДМ, а цифровое управления МП действует V t e [ t r , t r _{+ 1}) , r e N₀ с периодом Т Ц¹ >  T _u .

В данной статье решаются следующие задачи:

• (i)    разработка дискретных алгоритмов цифрового управления как МП, так и кластером ДМ с учетом особенностей их применения в СУО мини-спутника;

• (ii)    синтез нелинейного цифрового закона управления u _k = u ( a _k , to _k ) в эталонной модели (2) & (3) автономного наведения при ограниченных модулях векторов управления и угловой скорости, который обеспечивает асимптотическую устойчивость замкнутой непрерывно-дискретной эталонной модели;

• (iii)    синтез нелинейного цифрового закона управления кластером ДМ, который после завершения режима успокоения спутника обеспечивает переход КА из произвольной ориентации в ИСК в требуемое угловое положение в ОСК;

• (iv)    компьютерная имитация работы СУО в режимах начальной ориентации геодезического мини-спутника на солнечно-синхронной орбите при его автономном угловом наведении и управлении;

• (v)    краткое обсуждение проблем проверки работоспособности СУО мини-спутника.

ЦИФРОВОЕ УПРАВЛЕНИЕ МАГНИТНЫМ ПРИВОДОМ

Когда КА моделируется как твердое тело ( M ^d = 0 , M ^r = 0 и G = K ), управляемое только МП, то согласно (1) модель его динамики представляется в виде K = M — to х K , где K = K * = Jc o и внешний управляющий момент M = M ^m . Для синтеза локально оптимальных непрерывных законов управления M = M ( to ) применялась функция Ляпунова v = K ² = ( K , K ) . В результате установлено [4], что в режиме успокоения КА с минимальным принуждением M ² = | M | ² закон управления имеет вид M = — a K k с ортом k = K /К и постоянным параметром a >  0 , а закон управления M = — m k с постоянным параметром m >  0 представляет управляющий момент, оптимальный по быстродействию.

При цифровом управлении МП будем m считать, что в моменты времени t r = rT u вектор индукции магнитного поля Земли B r = B ( t r ) = B r b r измеряется магнитометром. При формировании команды M _r = — a K _r для вектора механического момента МП на каждом полуинтервале времени t е [ t r , t_{r + 1}) с заданным периодом T™ сначала определяется вектор потребной вариации импульса ( pulse ) управляющего момента

M f = j ⁺ М ( т ) d т = - a j ⁺ К ( т ) d т

• = - К r (1 - ехр( - aO) k r .

Этот вектор представляется в виде M p = b _r х ( M p х b _r ) + b _r ( M p , b _r ) и для энергетической экономичности МП назначается вектор M p = M p ^m = b _r х ( M p х b r ) с условием ( M p , b r ) = 0 .

Вектор потребной вариации импульса управляющего момента МП M p ^m = —A I m k _r с модулем A I “ = К _r (1 - ехр( - aT™) и ортом k _r далее используется для формирования цифрового управления ЭММ L _r = { l ir } МП с периодом T™ . При этом определяется взаимная ориентация ортов b _r и k _r , если | ( b _r , k _r )| >  cos( n /3) , то на текущем периоде дискретности МП не включается, иначе формируется вектор ЭММ L _r = ( A I ™ 1 7 _H ^m)( b _r x k _r )/ B _r с ограниченными компонентами | l r | <  l ^m .

ЦИФРОВОЕ УПРАВЛЕНИЕ ДМ

В задаче идентификации момента сил сухого трения по осям вращения ДМ для простоты рассмотрим только один ДМ, при этом индекс p не используется. Простейшая модель движения ДМ представляется в нормированном виде Q(t) = a(t) — af(t), где управляющее ускорение a = m / Jr, ускорение a f(t) = ao sign(Q(t) е [—af, af] отражает влияние момента сил сухого трения и при моменте инерции ДМ Jr параметр a0 = mf / Jr = const . В предположении af (t) = a f(ts) = as = const Vt е [ts, ts+1), где ts+1 = ts + Tq) с периодом Tq < Tu, для получения оценки as значения asf применяется дискретный идентификатор Луенбергера

Q s + 1 = Q s + ( a s — a i s ) T s + g f SQ s ;

af+1 = af + g2SQs; sqs+1 = qs+1 —Qs+1, где постоянные параметры gf и g2 определяются по явным соотношениям. Дискретная оценка момента сил сухого трения получается в f                f              f виде m (ts) = ms = Jr as.

Компенсационная схема разгрузки кластера ДМ основана на следующих положениях. Вычисляются потребная вариация модуля A I m и орт k _r вектора потребного импульса механического момента МП в ССК. Далее рассчитывается постоянная команда М ^ ^u = { m ™} =A I ^m b _r I T™ компенсации импульса механического момента МП, которая одновременно с периодом управления T_u^m поступает как на МП, так и с периодом управления T_u на кластер ДМ, но с обратным знаком.

Для кластера четырех ДМ принципиальная проблема заключается в распределении векторов его кинетического Н и управляющего М ^г =- Н моментов при избыточном числе двигателей- маховиков. При некоторых упрощениях эта проблема состоит в одновременном решении двух уравнений

A _Y h = Н V Н е R ³, V h е R ⁴;

A _Y m = Н * =- М ^г V М ^г е R ³, m е R ⁴.

Используемый подход к разрешению этих уравнений основан на применении скалярной функции автоматической настройки кластера, которая позволяет однозначно распределять векторы Н и М ^г =- Н между четырьмя ДМ по явным аналитическим соотношениям [6]. Введем нормированный вектор КМ кластера h = { x , y , z } = Н / Н ^т = A _Y h , где x = x 1 + x ₂ ,

X 1 = C Y ( h l + h 2 ) , x 2 = C Y ( h 3 + h ₄) ;

y = S 'Y ^{( h} 1 ^— h 2 ) , z = ^ Y ( h 3 — h 4 ) ;

h = { h p } , h p = h p /h ^m , | h p | < 1 .

Распределение этого вектора между четырьмя ДМ выполняется по закону

f

р = x - x2 + р(xx2 -1) = 0, где 0 < p <1; ~i = xi /qy;x2 = x2 / qz, qs = (4CY — s2)1/2, s = y,z, на основе соотношений

• (i)    q = q y ⁺ q z ;

a ( q / p )(l - (1 - 4 p [( q y - q z )( x /2)

+ p ( q y q z - ( x /2) ² )]/ q ² ) ^1/2 );

x 1 = ( x + A )/2 , x ₂ = ( x -A )/2 ;

• (ii)    распределение КМ между ДМ в каждой паре по очевидным формулам;

• (iii)    вычисление столбца m = { m p } по явной формуле

m = - ({ А y , a ^f}) ^{- 1}{( M k + M^X sat^, Ц р f , )} (4)

с параметрами ф_р , Ц_р >  0 и компонентами строки a ^f = [ a ^f ] в виде

,    2 C ' ,                  C ( h, + h. )

a f 2 =4" [2 C 2 ± S 2 h 2 ( h i — h 2 )][ 1 + P ² 3      ] ;

’      q y                                         q z

,   ² C                       C ( h + h ₂)

a f₄ =^[2 C 2 + S 2 h 4 ( h 3 — h 4 )][1 + P ² 1     ]

’       qz                                                  qy, с явным учетом команды Mku для приближенной компенсации влияния моментов МП при разгрузке кластера ДМ. В завершении формирования цифрового управления ДМ выполняется переопределение mк := mк + nf, где mf является столбцом, составленным из текущих оценок mк моментов сил сухого трения по осям вращения ДМ.

ЭТАЛОННАЯ МОДЕЛЬ НАВЕДЕНИЯ

При использовании диадного произведения [ а • Ь ] 3-мерных векторов a = { a i } и Ь = { b . } , которое представляется как [ а • b ] = ab ^t = С = || c ij || = || a i b j || , прямые и обратные кинематические уравнения для вектора МПР о имеют вид о = В ( о ) го и го = D ( o ) d , где матрицы

В ( о ) = 1 (1 -о ²) 1 ₃ +¹ ([ о х] + [ о • О ] ;

D ( o ) = В ^{- 1} ( о ) = (8/(1 + о ² ) ² ) B ^t ( о ) .

Компактное представление второй производной векторной функции о даётся соотношением

о = 1 (- о, О)го +1(1 - о2 )е + о х ®+ О х е + (о, ю)о + (о, ю)о + о(о, е).

В итоге модель (3) сводится к нелинейной управляемой системе в форме Бруновского о = v = Ь(о, го) + В(о)и, где векторная функция

Ь ( о , го ) = ([( В ( о ) го ) х ] + [ о ^ В ( о ) го )] го / 2 .

Применение методов линеаризации обратной связью, модального синтеза и векторных функций Ляпунова [7] для модели о = v на едином желаемом спектре S* = (-а± jв) с j = 7—1 приводит к непрерывному нелинейному закону управления v = -(коо + kгоо) = -(коо + кгоВ(о)го) с постоянными коэффициентами, который при обеспечении требуемой асимптотической устойчивости тривиального решения о (t) = 0, го (t) = 0 представляется в дискретном виде v к ={v к} = -(к d° к+к гов(о к)го к).

Здесь при заданном времени регулирования T r коэффициенты к ^d d и к “d вычисляются по явным аналитическим соотношениям to * = 3/( ^T r ) ; а = А -х, в = to * 4 1 -^ 2 ) ;

a 1 = - 2ехр( -а Т „ )cos( p T ), a 2 = exp( - 2 a T „ ); k 0 = (1 + a 1 + a 2 )/ T _M ², k to = (3 + a - a 2 ) /(2 T „ ), которые справедливы V ^ >  0 .

Предварительныйнепрерывныйзаконуправ-ления u = {wj = u(o, to ) = D(o)( v - b(o, to)) обеспечивает равномерную асимптотическую устойчивость тривиального решения для модели (3), а его дискретная форма представлена соотношением uk =-[D(ok)(k0°k + b(ok,tok)) + ktotok]. (5)

При окончательном формировании цифрового управления u _к ( о _к , го _к ) = { и_к } в очередной момент времени t k учитываются ограничения на модуль вектора управления ( u ( t ) <  u ^m ) и модуль вектора угловой скорости ( го ( t ) < го ^т ) по следующему простому алгоритму A :

• 1)    по значению цифрового управления и _к (5) в момент времени t _k вычисляется прогнозное значение вектора угловой скорости to к = to _k + u _k T _u , достигаемое в конце интервала времени длительностью T_u , и если | to к | > to ^m , то управление u _к переопределяется как u_k = ( (to ^m to_k p / to_k p ) - to_k )/ T_u ;

k      kk k u

• 2)    далее, если | u _к | = ~ _к >  u ^m , то формируется управление u _к = u ^m u _к / и_к , иначе u _к = ~ _к .

Для проверки работоспособности разработанного цифрового закона управления в эталонной модели наведения рассмотрим простейшую каноническую задачу. Пусть для эталонной модели наведения (3), определенной в ИСК, в момент времени to = 0 заданы начальные условия оо = ео tg(Фо/4), Фо = 120 град;

ео = {-0.165,0.537,0.826}; too = 0, закон цифрового управления uк (ок, гок ) с па- раметрами Tr = 60 Tu , ^ = 0,95, периодом Tu = 0,25 с представлен (5) с учетом алгоритма A и ограничения to™ = 1 град/c, u™ = 0.3 град/с2. Задача состоит в обеспечении совпадения ориентации ССК с ИСК, когда σ = 0 и ω = 0 .

На рис. 3 представлены переходные процессы для компонентов векторов σ , ω и ε ≡ u _k , а также для модулей векторов ω и ε (черный цвет). Здесь и далее компоненты векторов всегда отмечаются цветами: синий по оси O x крена, зелёный по оси O y рыскания и красный по оси O z тангажа. Эти результаты демонстрируют, что нелинейная модель (3) с цифровым законом управления u _k ( o _k , to _k ) асимптотически устойчива при ограничениях на модули векторов ω и u _k .

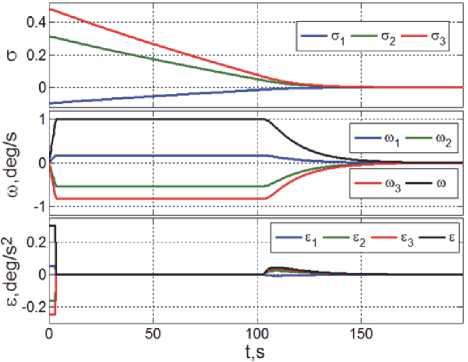
Рис. 3. Изменение векторов о, ю и управления е = uk

АВТОНОМНОЕ НАВЕДЕНИЕ И ЦИФРОВОЕ УПРАВЛЕНИЕ

Автономное наведение и цифровое управление основано на аналитических соотношениях, связывающих требуемые координаты состояния КА с измеренными координатами его углового перемещения. Задача заключается в синтезе законов автономного наведения и управления КА в начальных режимах ориентации, в том числе приведении КА из произвольной ориентации в ИСК к заданной в ОСК, для простоты совпадающей с этой системой координат. В таком случае кватернион Л ⁰ ( t ) определяет ориентацию ОСК в ИСК и получается закон наведения Л p = Л ⁰ , to p = to ⁰ и 8 p = 8 ⁰ . В ОСК O x ⁰ y ⁰ z ⁰ ориентация КА определяется также углами Эйлера-Крылова ф 1 (крена), ф ₂ (рыскания) и ф ₃ (тангажа) в последовательности 312 элементарных поворотов. Эти углы составляют столбец ф = {ф i } и используются при формировании матрицы C ⁰ = C ^е .

Все кинематические параметры ( Л ⁰ , to ⁰ ,

• 8 ⁰ )    углового движения ОСК в ИСК формируются непосредственно на борту мини-спутника,

Гт _   ___ _ и при его успокоении в

ИСК и затем с периодом T_u при использовании методов фильтрации, аппроксимации, интерполяции и экстраполяция [1]. С другой стороны, кватернион Λ ориентации КА в ИСК и вектор ω его угловой скорости измеряются БИНС и кластером ДУС, поэтому и возникает возможность автономного наведения [5] и цифрового управления ориентацией мини-спутника в РНО.

Предположим, что КА отделяется от ракеты-носителя в момент времени t ₀ = 0 , когда вектор угловой скорости to ( t ) принимает значение to ₀ = to ( t ₀) с полностью произвольным кватернионом Л 0 = Л ( t 0 ) его ориентации в ИСК. Как подробно описано выше, цифровой вектор ЭММ L r = { l ir } с ограниченными компонентами | l ir | < 1 ™ начинает формироваться автономно, используя измерения магнитометра и кластера ДУС: генерируются значения вектора M ^m ( t ) = { m ^m ( t )} V t e [ t r , t r _{+ 1}) для замедления вращения КА и режим его успокоения в ИСК заканчивается, когда выполнено условие | to ( t ) | < to , = to ( t ^ ) в некоторый момент времени t ₁ ^∗ . В тот же момент времени значения Л _{# 1} = Л ( t*_x ) и to j = to ( t*_x ) измеряются БИНС, которые далее используются при расчете начальных условий для приведения ориентации ССК к заданной в ОСК.

При t ≥ t ₁ ^∗ измеряемые Λ _k , ω _k и формируемые на борту КА переменные Л k , to _k ⁰ , 8 _k ⁰ применяются для расчета значений o k = e k tg( Ф k /4)^ , C k , o k = e k tg( Ф k /4) , to k 3 to _k = to _k - C k to k и З ф _k . Это позволяет вычислить вектор цифрового управления кластером ДМ по соотношению

M k = to k x G 0 + J ( C k 8 0- + [ C k to 0 x ] to k + m k ) , (6) где вектор G k = К _k + H _k , а вектор m _k формируется в соответствии с двумя этапами:

• 1)    V t e [ t * , 1 ₂ * ) пока ф ^e ( t ) > Ф е2 =Ф ^e ( 1 ₂ * ) при заданном значении ф e ₂ в некоторый мо *

мент времени t = 1 ₂ , вектор m _k рассчитывается с использованием эталонной модели наведения по ошибке o k вектора МПР как

~е          е d е       ее      d,х е u к = -[ D (° k)(k с° k + b (ak, to к)) + к Юю к ], (7) но с учетом общих ограничений на модули век торов ω и uk в алгоритме A , см. также (5);

• 2)    V t >  t * стабилизирующий вектор m _k формируется так: выполняется фильтрация значений вектора углового рассогласования 8 _l = -З ф _l , l e N₀ с периодом T p и результи-

• рующие векторы εfk, k ∈ N0 используются для вычисления значений вектора m~ k по соотношениям

g,+,= Bg, + Ce^; m, = К(g, + Pe^), (8) k + 1 k k k k k где при du = 2/Tu и a = (duT, —1)/(duT, +1) элементы диагональных матриц B , P и C вычисляются в виде b = (duT2 -1) /(duT2 +1); p = (1 - b)/(1 - a); c ≡ p(b-a) с параметрами τ1 и τ2.

РЕЗУЛЬТАТЫ КОМПЬЮТЕРНОЙ ИМИТАЦИИ

Пусть мини-спутник массой 250 кг при выводе на солнечно-синхронную орбиту высотой 600 км, наклонением 97.787 град и долготой восходящего узла 30 град, пролетая над восходящим узлом орбиты в момент времени t0 = 0 отделяется от ракеты-носителя и начинает кувыркать- ся с модулем вектора угловой скорости ω 0= 3 град/с. Предположим, что МП имеет ограничение lm = 10 А м2 для компонент вектора ЭММ и период Tum = 4 с цифрового управления MП, а в цифровом законе управления uk(σk,ωk) кластером ДМ (6) с периодом Tu = 0.25 с и ограничениями ωm = 1 град/c, um = 0.3 град/c2 коэффициенты kσd и kωd были рассчитаны с параметрами Tr = 60 Tu и ^ = 0.95.

На рис. 4 представлены результаты компьютерной имитации изменения вектора угловой скорости ω ( t ) мини-спутника при цифровом управлении как МП, так и кластером ДМ во всех начальных режимах ориентации. Здесь для заданного значения ω₁^∗= 0.5 град/с автоматически определяется момент времени t ₁^∗ = 6336 с завершения режима успокоения КА, а также значения Л . 1 , ® * , o^ = e * ₁ tg( Ф ® ₁/4) при

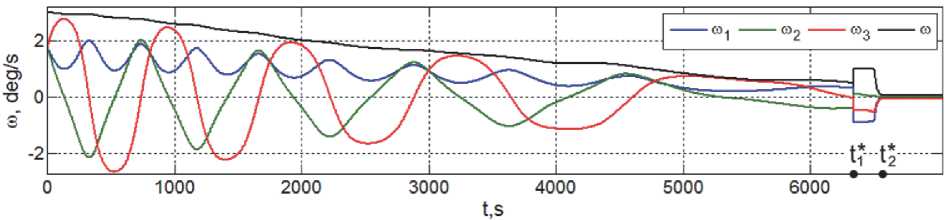
Рис. 4. Изменение вектора угловой скорости при цифровом управлении МП и кластером ДМ

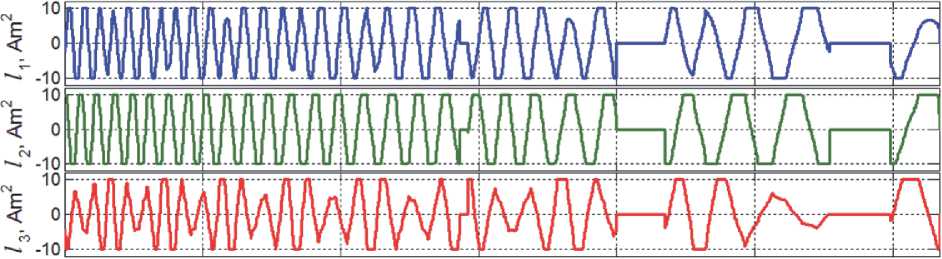
0           1000          2000          3000          4000          5000          6000

t,S

Рис. 5. Изменение вектора электромагнитного момента при цифровом управлении МП в режиме успокоения

О            1000          2000          3000          4000          5000          6000

t,s

Рис. 6. Изменение вектора механического момента при цифровом управлении МП в режиме успокоения

Φ _* ^e ₁ = 175.56 град и ω _* ^e ₁ = ω _*1 - C _* ^e ₁ ω _* ^o ₁ . Изменения векторов L и M ^m магнитного привода в этом режиме представлены на рис. 5 и 6. При заданном значении Φ _* ^e ₂ = 0.083 град векторный закон m ^~ _k в (6) переключается от (7) к (8) в момент времени t ₂^∗ = 6583.6 с. Изменение углов Эйлера-Крылова 5ф 1 (крен, синий цвет), 5ф 2 (ры-скание, зеленый), δφ₃ (тангаж, красный) и угол Φ ^e (черный цвет) собственного поворота КА в ОСК ∀ t ≥ t ₁ ^* = 6336 с представлены на рис. 7, а некоторые детали изменения векторов ω , M ^r и m в процессе приведения ориентации КА в ОСК – на рис. 8, 9 и 10. Наконец, на рис. 11 и 12 приведены ошибки по угловым скоростям δω _i и углам δφ _i при переходе СУО в установивший режим угловой стабилизации мини-спутника в орбитальной системе координат.

Здесь были учтены все шумы измерений и возмущающие моменты, тщательная дискрет- ная фильтрация измерений и выбор параметров в автономных цифровых законах управления позволили добиться хороших результатов по точности СУО мини-спутника в начальных режимах его ориентации.

ПРОВЕРКА РАБОТОСПОСОБНОСТИСИСТЕМЫ УПРАВЛЕНИЯ ОРИЕНТАЦИЕЙ

Проверка работоспособности СУО в режимах начальной ориентации является весьма ответственной, здесь требуется особая тщательность при определении работоспособности кластера ДМ. В случае отказа необходимо провести быструю диагностику с определением конкретного отказавшего двигателя-маховика.

Алгоритм бортовой диагностики состояния СУО использует её эталонную модель для имитации номинального управления движением КА в реальном времени. Здесь для обнаружения аномальной ситуации на каждом контрольном

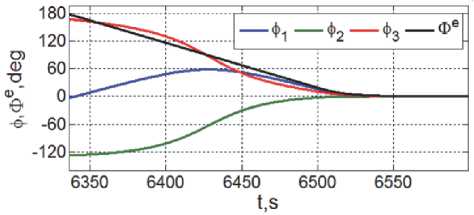
Рис. 7. Углы Эйлера-Крылова и угол вращения КА в ОСК

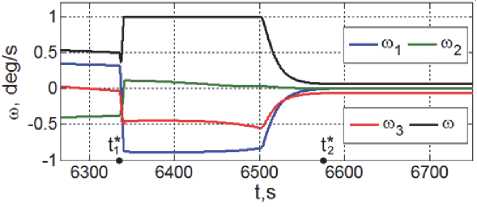
Рис. 8. Изменение вектора ю при приведении КА к ОСК

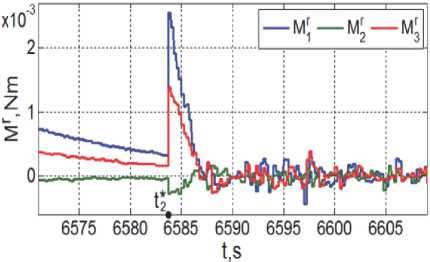
Рис. 9. Изменение вектора моментов кластера ДМ

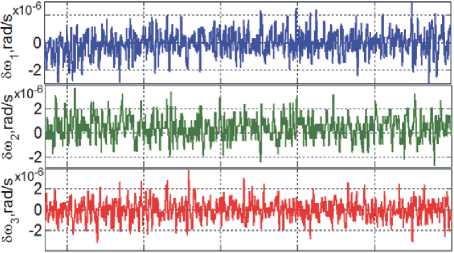
6800     6900     7000     7100     7200

t,s

Рис. 11. Изменение вектора Зю в режиме стабилизации КА

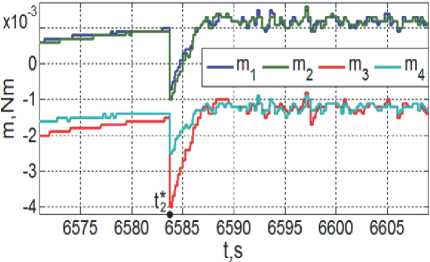
Рис. 10. Изменение управляющих моментов четырёх ДМ

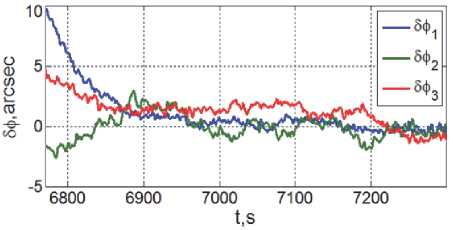
Рис. 12. Изменение вектора Зф в режиме стабилизации КА

периоде вычисляется вектор рассогласований e = { e i } = x — x между векторами измеренных x = { x, } и моделируемых x = { x i } координат.

Применяемый подход к диагностике СУО и принятию решения о неисправности заключается в следующем. Изменение во времени диагностических параметров e j ( t ) с индексом отказа j = 1,2 можно рассматривать как случайный процесс, характеристики которого зависят от множества факторов. Поэтому классификацию нужно вести не по детерминированным мгновенным значениям рассогласований e j ( t ) в конце каждого контрольного периода T_u , а как случайный процесс, представленный дискретной последовательностью значений e j k = e j ( t k ) , t k _{+ 1} = t k + T u для скользящего окна таких измерений. Классификация отказов с использованием обработки данных случайного процесса в таком окне реализована в нашей модификации [8] алгоритма последовательного контроля отношения вероятностей (ПКОВ, A. Wald , 1954), детали представлены также в [9].

ЗАКЛЮЧЕНИЕ

Для приведения ориентации космического аппарата от произвольной к требуемой используется автономное угловое наведение и модульно ограниченное векторное цифровое управление с применением вектора модифицированных параметров Родрига. Автономные векторные цифровые законы управления магнитным приводом и минимально избыточным кластером двигателей-маховиков применяются соответственно для успокоения кувыркающегося мини-спутника после его отделения от ракеты-носителя и приведения его ориентации в заданное положение в орбитальной системе координат без какой-либо реактивной двигательной установки.

Основными достижениями работы являются: (i) автономное векторное цифровое управление минимально-избыточным кластером двигателей-маховиков при явном распределении вектора управляющего момента между маховиками с учетом ограниченных ресурсов кластера по векторам управляющего момента и кинетического момента; (ii) разгрузка кластера двигателей-маховиков от накопленного кинетического момента при помощи магнитного привода с цифровым управлением по оригинальной схеме компенсации; (iii) встроенная дискретная идентификация и цифровая компенсация момента сил сухого трения на оси вращения каждого маховика.

Представлены разработанные методы и алгоритмы автономного наведения и цифрового управления мини-спутником землеобзора в на- чальных режимах ориентации, а также результаты компьютерной имитации с учетом всех шумов измерений и возмущающих моментов. Эти результаты продемонстрировали хорошую точность системы ориентации мини-спутника, достигаемую тщательной дискретной фильтрацией измерений и выбором параметров в простых цифровых законах управления. Кратко рассмотрена проблема проверки работоспособности системы ориентации мини-спутника и представлены разработанные дискретные алгоритмы бортовой диагностики и классификации отказов, основанные на компьютерной обработке доступных измерений и явных соотношениях.

Разработанные алгоритмы автономного наведения, цифрового управления и мониторинга состояния миниатюрных геодезических спутников просты, надежны и реализуемы в космической технике [1].