Автономное наведение и управление ориентацией космического аппарата в режиме слежения

Проблемы динамического синтеза и нелинейного анализа систем управления ориентацией (СУО) космических аппаратов (КА) остаются актуальными для его пространственного углового движения. В статье основное внимание фокусируется на нелинейностях кинематических соотношений при управлении пространственным угловым движением КА с ограничениями на модули векторов угловой скорости и управляющего момента. Управление ориентацией КА выполняется магнитным приводом (МП) и кластером четырех реактивных двигателей-маховиков (ДМ) по сигналам бесплатформенной инерциальной навигационной системы (БИНС) с коррекцией от спутников GPS/ГЛОНАСС и звездных датчиков, а также сигналам гироскопических датчиков угловой скорости (ДУС). После отделения от ракеты-носителя КА начинает кувыркаться – вращаться с вектором угловой скорости ω изменяемого направления в базисе B , связанного с его корпусом. Выделяются начальные режимы ориентации [1]: (i) успокоение КА в инерциальном базисе I помощью управ-

ления МП; (ii) включение кластера ДМ в контур управления КА с разгрузкой этого кластера от накопленного кинетического момента (КМ) с помощью магнитного привода; (iii) угловое наведение и управление КА с приведением ориентации спутника к заданной в орбитальном базисе O . В наших последних публикациях [2] - [6] при решении задачи (iii) применялся закон углового наведения в виде набора векторных сплайнов в зависимости от времени. В отличие от такого подхода, здесь первые решается задача автономного углового наведения КА при слежении за эталонной моделью по доступным измерениям и цифрового управления кластером двигателей-маховиков с автоматическим приведением ориентации спутника к заданной в орбитальном базисе.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ

Минимально-избыточная схема General Electric ( GE ), рис. 1, обладает возможностью управлять ориентацией КА при отказе любого одного маховика. Здесь в базисе B (системе координат O xyz ) оси вращения четырёх ДМ располагаются на поверхности конуса с углом полураствора γ . Далее используются стандартные обозначения { • } = col0 , [ • ] = line( - ) , ( • , • ) , ( - ) ‘ , [ a x ] и ° ,~ для векторов, матриц и кватернионов, C _Y = cos у , S _Y = sin у , i = 1,2,3... m = 1 ^ m и применяется вектор модифицированных параметров Родрига (МПР) ст = { ст i } = e g ( Ф /4) с традиционными обозначениями орта Эйлера e и угла Φ собственного поворота. Вектор σ взаимно-однозначно связан с кватернионом Л = ( X ₀, X ) , Х = { X i } ориентации КА в инерциальном базисе I прямыми

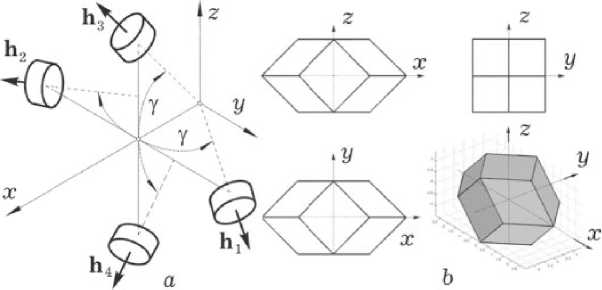
Рис. 1. Схема GE ( a ) и оболочка ее КМ ( b )

О = X/ (1+ X 0) и обратными X 0 = (1 -О 2)/(1 + О2) , X = {Xi} = 2о/(1+ О2) аналитическими соотношениями. Модель углового движения КА учиты вает упругость его конструкции и имеет вид

Л = Л о ю/2 ; A ° { ю , q , Q } = { F “ , F ^q, F ^Q } , (1) F “ =- [ ю x ] G + M ^m + M ^d ;

F ^q = — A q ( V q q + W q q ) ; f ^Q = m — m ^f ;

A ° =	J d : _ Jr A Y " C Y	D Ч A4 0		J r A y 0 Jr 1 4 _ C Y	’
		C Y	C Y
A Y =	^ Y	" ^ Y	0	0
	0	0	^ Y	- 5	Y J

A q = diag{ ц _у }; V _е = diag{|Q s }

W q = diag{( Q s )²}; M ^m = { m ™ };

M = { m_p }; M ^f = { m p };

вектор

механического момента МП Mm = {m™} = =-L X B [7], где вектор электромагнитного момента (ЭММ) L = {li} с ограниченными компонентами | li |< lm и вектор индукции магнитного поля Земли B = b B с ортом b определены базисе B ; векторы-столбцы M = {mp} и M = {mp} представляют управляющие моменты и моменты сил сухого трения по осям вращения ДМ, а вектор Md - внешние возмущающие моменты. Ресурсы каждого ДМ по управ- ляющему и кинетическому моментам ограничены, | mp(t) |< mm,| hp(t) |< hm, p = 1 -4.

Вектор M ^r управляющего момента кластера ДМ формируется в виде M ^r = - H , где ( • ) * - символ локальной производной по времени. Если корпус КА считать твердым телом, то G = G ° и модель динамики его углового движения принимает вид

Jco + [ юх ] G = M ^r + M ^m + M ^d . (2)

Пусть измерение кватерниона ориентации КА Л m — Л ^m ( t l ) выполняется с периодом T_p , где Л ^m ( t l ) = Л ( t l ) о Л ” и кватернион Л П = Л ” ( t l ) представляет центрированный гауссовский шум, t l _{+ 1} = t l + T_p , l е N₀ — [0,1,2,3...) , а измерение угловых скоростей вращения ДМ Q ps = Q p ( t s ) - в моменты времени t s с периодом T q , t s ₊ 1 = t s + T q , s е N₀ . Будем считать, что в моменты времени t k с периодом T u , t k + 1 = t k + T u , ^{k е} N o измеряется вектор угловой скорости to _k — ю ( t k ) корпуса КА и формируется цифровое управление ДМ, а в моменты t_r с периодом T u ^m >  T u , t _{+ 1} = t + T u ^m, r е N_o измеряется вектор индукции B r - B ( t r ) магнитного поля Земли и формируется цифровое управление МП, когда значения компонентов вектора ЭММ L = { l i } фиксируются V t е [ t_r , t_{r + 1}) .

ПОСТАНОВКА ЗАДАЧИ

Будем считать, что электромеханическая СУО при модели КА в виде твердого тела при отсутствии внешних возмущений ( M ^m = 0 ; M ^d = 0 в модели (2)) является сбалансированной по вектору суммарного кинетического момента, что соответствует тождеству G = G ° = K + H - 0 . Тогда пространственное угловое движение КА описывается уравнениями

Л = Л ° о/ 2; го = J-1Mr =г = и. (3)

Пусть для формирования управления u применяются измерения кватерниона Л ( t ) , которые используются для вычисления вектора МПР

a(t), и вектора угловой скорости to (t). Кинематическому уравнению в (3) соответствует соотношение a = (1 -о2)ю/4 + ахю/2 + a(a, to)/2 для вектора МПР σ , поэтому при векторе управляющего углового ускорения u ≡ ε модель (3) представляется в нормированной непрерывной векторной форме а = ^(1 o' )to-1ахю + 1a(a,to); to = u (4) с заданными начальными условиями а(to) = a, , to (to) = toj при to = 0, где при обозначении eo = e(to) вектор a, = e0£(Фo/4) является произвольным с условием | Фo |< 2п.

Как известно, кватернион - Λ задает вращение КА на угол 2 п — Ф вокруг орта Эйлера - e , которое полностью совпадает с вращением этого объекта на угол Φ вокруг орта Эйлера e , т.е. значения Λ и - Λ совпадают. Следовательно, при Φ = π возникает проблема двузначности кватерниона и требуется конкретизировать его значение вместе с направлением орта Эйлера. Для вектора МПР ^σ такая проблема не проявляется VФe ( — 2 п , 2 п ) . Поэтому мы детально изучаем эталонную модель автономного пространственного наведения с вектором МПР σ , вектором угловой скорости ω и вектором ускорения ε ≡ u , который формально считается управлением. Будем считать, что вектор такого управления u = {u i } ограничен по модулю | u ( t )| = u ( t ) <  u^m , u^m >  0 , а вектор to ( t ) = { to i ( t } ограничен по модулю | to ( t )| = to ( t ) ^m , to ^m >  0 , естественно to j = | to _o | ^m.

Первая задача состоит в синтезе векторного нелинейного закона цифрового управления uk = u(ak, tok) (5) для эталонной модели автономного наведения (4) в моменты времени tk, k e N0 с периодом дискретности Tu = tk+1 — tk и ограниченными модулями векторов управления и угловой скорости, который обеспечивает асимптотическую устойчивость тривиального решения замкнутой нелинейной непрерывно-дискретной системы (4), (5) с выполнением условия lim| a (t )| = 0 , lim|to (t )| = 0. (6) t→∞ t→∞

Вторая задача заключается в синтезе цифрового закона управления кластером ДМ, который обеспечивает переход КА из произвольной ориентации в малую окрестность его требуемого углового положения относительно желаемого углового движения КА в заданный момент времени. При этом система векторных соотношений (4), (5) применяется как эталонная модель автономного углового наведения КА по доступным измерениям.

Наконец, третья задача состоит в синтезе экономичного цифрового управления КА в режимах начальной ориентации, когда практически используется автономное угловое наведение КА по доступным измерениям в замкнутом контуре управления.

ЭТАЛОННАЯ МОДЕЛЬ НАВЕДЕНИЯ

При использовании диадного произведения [ a • b ] 3-мерных векторов a = {a i } и b = { b j } , которое представляется как [ a • b ] = ab ‘ = C = || c ij || = || a i b j || , кинематическое уравнение в (4) принимает вид

O = (1(1 -52)I3 +1 ([ox] + [O • o])to = B(o)to (7) с обратным векторно-матричным соотношением to = B-*(o)O = (8/(1 + o2)2)B‘(o)d.   (8)

Вторая производная а вектора МПР ^a получается дифференцированием (7) по времени, что приводит к выражению

O = 1(-(O, <5 )to +1(1 -O2)£ + O Xto+ o x e+(o, to)O + (O, to)o+o(o, e).

В итоге модель (4) сводится к нелинейной управляемой системе в форме Бруновского a = v = b(a, to) + B(a)u,       (9)

где векторная функция b ( a , to ) представляется в виде b ( o , to ) = ([( B ( o ) to ) x ] + [ O ^ B ( o ) to ]) to / 2 .

В соответствии с методом линеаризующей обратной связи сначала выполняется синтез закона вспомогательного управления v(a, a) для линейной системы a = v. При модальном синтезе на едином желаемом спектре S * = (—a ± j в) по каждому замкнутому каналу ориентации КА получается непрерывный закон управления v = —( k „a + k toa) = —(k „a + k toB(a)to) , который при обеспечении требуемой асимптотической устойчивости (6) тривиального решения a (t) = 0, to (t) = 0 представляется в дискретном виде vk={vk}=—(kdak + ktoB(ak)tok). (io)

Здесь при заданном времени регулирования Tr коэффициенты kσd и kωd вычисляются по явным аналитическим соотношениям to* = 3/(^7; );

a = ^to*, в = to* 71-12);

a 1 = -2 exp(-aTu) cos(e Tu), a 2 = exp(-2a Tu);

k dd= (1 + a 1 + a 2)/Tu\ kto = (3 + a 1 - a2)/(2Tu), которые справедливы V ^ > 0. Отметим, что вычислении коэффициента a 1 со значением ^ > 1 получается функция cos(j x) мнимого аргумента, которая автоматически превращается в гиперболический косинус cosh( jx) = (exp(-x) + exp(x) /2. В этом случае желаемый спектр S* принимает значение S* = (-а, ,-а2), где а1 - го*(^-д/^2 -1) и а и.(2- х2 1).

Предварительныйнепрерывныйзаконуправ- ления и = {uj = u(a, to) = В 1(о)(v - b(a, to)) определяется в явном аналитическом виде, а его дискретная форма представляется соотношением и k = 4-Ат В ‘(ak)(k ..о k d + °k)                         (11)

+ b ( a k , to k )) + ( k ^ /2) to k ].

При окончательном формировании цифрового управления u _k ( a _k , to _k ) - { u_k } в очередной момент времени t k учитываются ограничения на модуль вектора управления ( u ( t ) <  u^m ) и модуль вектора угловой скорости ( го ( t ) ^m ) по следующему простому алгоритму: 1) по значению цифрового управления u _k (11) в момент времени t k вычисляется прогнозное значение вектора угловой скорости to q = to _k + ^u _kT_u, достигаемое в конце интервала времени длительностью T_u , и если | to q | > to ^m , то управление u _k переопределяется как и _k = ( (to ^m to P / to P ) - to _k ) / T u ; 2) далее, если | u _k I - ^u k >  u m , то формируется управление u _k = u u _k I u_k , иначе u _k = u _k .

На рис. 2 представлены переходные процессы для компонентов векторов a, to и е - u , а также для модулей векторов to и е (черный цвет), при начальных условиях aо = ео ‘g(Фо /4), Фо = 176.039 град;

е _о = { - 0.168295301056269,

0.520778421886236, 0.83693878326916};

too = {-0.0718, 0.0684,0.06701} град/с, параметрах Tr = 100 Tu, ^ = 1.5 цифрового закона управления (11) с периодом Tu = 0,25 с и ограничениях tom = 1 град/c, um = 0,15 град/с2.

АЛГОРИТМЫ АВТОНОМНОГО НАВЕДЕНИЯ И УПРАВЛЕНИЯ

Задачи наведения информационных спутников обычно формулируются в геодезическом базисе, связанном с вращающейся Землей. При этом законы автономного наведения основываются на аналитических соотношениях, связывающих координаты состояния спутника с измеряемыми координатами объектов информационного обслуживания. При автономном наведении космических роботов применяются измеряемые координаты подвижной цели.

Рассмотрим простейшую задачу, которая состоит в синтезе закона автономного углового наведении КА при его переходе из произвольной ориентации в орбитальную. Ориентация орбитального базиса O (системы координат O x ^o y ^o z ⁰ ) в инерциальном базисе I определяется матрицей C o и кватернионом Л ⁰ . В свою очередь, угловое положение базиса B относительно базиса O представляется углами крена ф 1 , рыскания ф ₂ и тангажа ф ₃ в последовательности поворотов 312 и кватернионом невязки Е = ( е ₀, е ) = Л ^о ° Л с вектором e = { е, } , которому соответствуют вектор параметров Эйлера

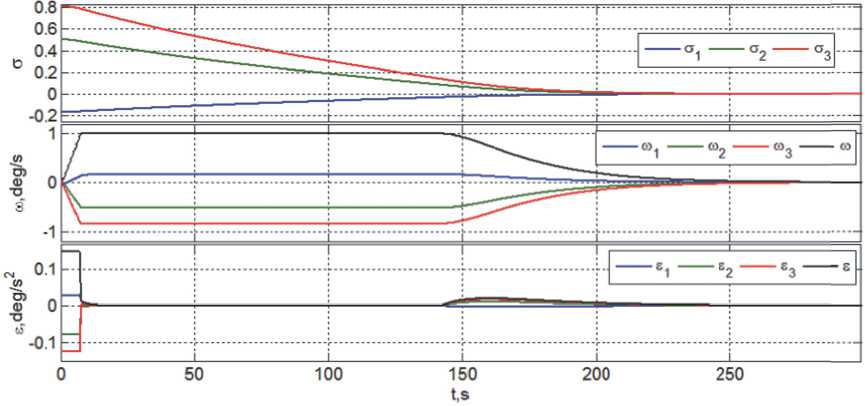
Рис. 2. Изменение векторов a и to при цифровом управлении е - u _k в эталонной модели наведения

^e -e_

E = {e₀, e } , матрица C ^e( E ) = 1 ₃ - 2[ e x ] Q e , где Q _e = 1 ₃ e ₀ + [ e x ] , вектор мпр G ^е = e /(l + e ₀) = = e ^е tg( Ф ^е/4) и вектор-столбец погрешности ориентации 5 ф = {5ф i } = { 2 е ₀ ej . Вектор невязки по угловой скорости вычисляется по соотношению S w = го — С ^е ю ° , где го ° является вектором абсолютной угловой скорости базиса O .

Применяемая стратегия автономного углового наведения КА содержит два этапа:

• 1)    угловое наведение КА при его переходе из произвольной ориентации в малую окрестность его требуемого углового положения в инерциальном базисе, когда используется эталонная модель автономного углового наведения (11) с учетом ограничений по дискретным измерениям в базисе B кватерниона ориентации Л k и вектора угловой скорости to k космического аппарата;

• 2)    автономное угловое наведение КА в малой окрестности движения орбитального базиса на основе требования для кватерниона навязки Е k = Л k ° Л k = 1 с единичным кватернионом 1 по измерениям как кватерниона ориентации Л k базиса O , так и кватерниона ориентации Л k базиса B , в инерциальном базисе I .

В процессе обработки в БИНС сигналов навигационных спутников GPS/ГЛОНАСС на борту КА формируются значения векторов расположения r ₀ и скорости v ₀ поступательного движения его центра масс в инерциальном базисе I . При определении орта радиали r ⁰ = r ₀ / r_o и орта v ⁰ = v _o / v₀ положение ортов нормали n ⁰ и трансверсали т ⁰ в произвольной точке орбиты вычисляется по алгоритму n ⁰ = ( r ⁰ x v ⁰)/| r ⁰ x v ⁰ | , т ⁰ = n ⁰ x r ⁰ , а орты o ₁ , o ₂ и o ₃ орбитального базиса O назначаются в виде o ₁ = т ⁰ , o ₂ = r ⁰ и o ₃ = — n ⁰ . Ортогональная матрица C ⁰ = ( c ij ) , / , j _e 1 ^ 3 ориентации базиса O в базисе I формируется как С ° = {[ о i ]} , i e l ^ 3 , соответствующий кватернион Л ° = ( X ° , X ° ) вычисляется по явным соотношениям

X 0 = (l + tr С ° )^l/2/2;

X ° = ( с ° + 1 i + 2 — c °+ 2 i + i )/(4 X ° ) ;

i = 1 ^ 3, i + 3 = i , при этом для исключения неопределенности типа (0/0) в процессе вычисления X 0 при значении X ⁰ = 0 используется известный алгоритм С. Стенли. С другой стороны, подсистема определения ориентации в составе БИНС выполняет измерение фактической ориентации связанного базиса B в инерциальном базисе I , результат измерения отражается кватернионом Л .

Задача синтеза законов автономного углового наведения и управления ориентацией КА заключается в создании эталонной модели с ограниченными модулями векторов скорости и ускорения для совмещения базиса B , имеющего произвольное начальное положение при кватернионе Л ( t ₀) = Л ₀ , с базисом O по значениям кватернионов Л и Л ^о и вектора угловой скорости to корпуса КА, а также векторов угловой скорости to ° и углового ускорения Е ° = (О ° базиса O для совмещения базиса B при его движения в малой окрестности орбитального базиса.

Рис. 2 демонстрирует, что при ограничениях to ^m = 1 град/c, u^m = 0,15 град/с² совмещение произвольного положения базиса B с инерциальным базисом ^I гарантированно завершается за время T * = 300 с. Очевидно, что малой длительности совмещения фактическую орбиту КА с периодом « 2 ч можно аппроксимировать керлеровой орбитой в центральном гравитационном поле Земли. При общепринятых обозначениях такую орбиту описывают шесть кеплеровых элементов - долгота восходящего узла Q и наклонение i орбиты; фокальный параметр p , эксцентриситет e и широта to_n перицентра орбиты, а также момент времени t _п , при котором радиус-вектор центра масс КА направлен на перицентр. Текущее положение КА в момент времени t определяется в угловой мере истинной аномалией v ( t ) , которая отсчитывается от перицентра to_n в направлении его движения, при этом вектор угловой скорости to ° = v ( t ) о ₃ и вектор углового ускорения Е ° = О ° = v ( t ) о ₃ орбитального движения центра масс КА.

По измеренным БИНС в момент времени 1 ₀ значениям векторов расположения r ₀ и скорости v ₀ поступательного движения центра масс КА (шесть координат состояния) на его борту по явным аналитическим соотношениям [8] вычисляются сначала значения кватерниона Л ° ( t ° ) = Л ° , шести кеплеровых элементов орбиты и вектора угловой скорости to ° ( t ° ) = О ° , а затем прогнозируемые значения постоянного кватерниона Л ° ( t , ) = Л ° и вектора угловой скорости О ° ( t , ) = О ° в базисе I для момента времени t * = 1 ₀ + T r .

Кватернион ориентации базиса B относительно инерциального базиса I представим в виде Л = Л ° ° Ле, где кватернион Ле = Л° ° Л соответствует вектору МПР Ge = {Gе} = eе tg(Фе / 4) эталонной модели наведения с векторами угловой скорости юе = Л ° ° ю ° Л ° и углового ускорения Ее = Uе =Л ° ° Е ° Л °. Цифровой закон управ- ления uek = {uk} = uk (оk, tok ) в такой эталонной модели наведения формируется согласно (11) по измеренным значением Лk, tok и далее вычисленным значениям Оk, tok с учетом ограничений на модули векторов скорости tok и ускорения uk. При этом вектор управляющего момента КА Mk с применением эталонной модели автономного углового наведения формируется в виде

М k = Ju k + to k x G k ,        (12)

где u _k = Л ° о u k о Л ° и G _k = Jto _k + H _k .

При малой невязке углового положения базиса B относительно базиса O выполняется фильтрация значений вектора углового рассогласования e _l = —5ф _l = - 2 e_0l е _l , l e N₀ с периодом T p и формируются векторы £ f , k e N₀ , которые используются в законе управления кластером ДМ ^                         ^

g k + 1 = Bg k + c e k ;     m _k = К ⁽ g _k + ^p e J;

(13) М k = tok x Gk + J(Ck e: + [Ck to>]to k + mk)

с периодом Tu, где Gk = Jtok + Hf и при обозначениях du = 2/Tu, a = (duTi-1)/(duTi +1) элементы диагональных матриц B, P и C вычисляются в виде b = (du T2 -1) /(duT2 +1); p = (1 - b)/(1 - a); c = p(b — a) с настраиваемыми параметрами Т1, т2, а также k в диагональной матрицы K.

УПРАВЛЕНИЕ КЛАСТЕРОМ ДВИГАТЕЛЕЙ-МАХОВИКОВ

В задаче идентификации момента сил сухого трения по осям вращения ДМ для простоты рассмотрим только один ДМ, при этом индекс p не используется. Простейшая модель движения ДМ представляется в нормированном виде Q ( t ) = a ( t ) — a ^f( t ) , где управляющее ускорение a ( t ) = m ( t )/ J r , ускорение a ^f( t ) = a О sign( Q ( t ) e [ — a ^f, a ^f] отражает влияние момента сил сухого трения и при моменте инерции ДМ J r параметр a О = m О I J_r = const . В предположении a ^f( t ) = a ^f( t s ) = a s = const V t e [ t s , t s _{+ 1}) для получения оценки a s значения a_s применяется дискретный идентификатор Луенбергера

Q s + i = Q s + ( a s — a i s ) T s + g f 5Q s ;

a = af + g2 5Q s; 5Qs+i = Qs+i — Qs+i с периодом T , где постоянные параметры q g1 и g2 определяются по явным аналитическим соотношениям. Дискретная оценка момента сил сухого трения получается в виде m (ts) = ms = Jr as .

Компенсационная схема разгрузки кластера ДМ основана на следующих положениях. Вычисляются модуль Im и орт em вектора потребного импульса механического момента МП в базисе B , назначается его вариация AIm на периоде T™ цифрового управления МП и рассчитывается Меи      сил лтт^т / mm k = {mik } =Д1 е / Tu компенсации импульса механического момента МП, которая с периодом цифрового управления Tu поступает на кластер ДМ. Здесь в моменты времени tr, r e N0 вычисляется орт b r = B r IB r и определяется взаимная ориентация ортов br и em в базисе B; если | (br,em)|> cos(n/3), то на очередном периоде дискретности МП не включается, иначе вычисляются вектор Lr = {li} = AIm(br x em)IBr потребного электромагнитного момента МП на очередном шаге цифрового управления МП с периодом Tum .

Для кластера четырех ДМ принципиальная проблема заключается в распределении векторов его кинетического H и управляющего M ^r=- H * моментов при избыточном числе двигателей-маховиков. При некоторых упрощениях эта проблема состоит в одновременном решении двух уравнений