Автосинхронизация колебаний в сложных системах

Введение. В настоящее время проблемы синхронизации широко обсуждаются в различных областях науки и техники. В частности, известно, что огромную роль синхронизация колебаний играет в экологических и биологических системах. Так, процессы в большинстве живых систем синхронизируются с цикадными и сезонными ритмами. Примерами сложных технических систем могут служить энергетические сети. В энергетике синхронизация колебаний позволяет автогенераторам, генераторам переменного тока и другим нелинейным системам устойчиво работать в синхронном режиме в пределах конечной полосы частот, а также дает возможность нескольким генераторам обеспечить надежную работу на общую сеть энергосистемы.

В сложных нелинейных системах, генерирующих несколько частот, возможна синхронизация колебаний на различных комбинациях частот.

Как отмечается в работах [1–4], важную роль в процессах синхронизации взаимодействующих генераторов играет структура, в которую они встроены. Это могут быть системы, организованные по принципу цепочки или магистрали, а также системы с радиальными или глобальными (каждый с каждым) схемами взаимных связей. Например, при цепочной структуре колебательной системы сила связи между ее элементами убывает с увеличением расстояния между ними. Более сложные процессы синхронизации возникают в замкнутых структурах, состоящих из большого числа взаимодействующих осциллирующих элементов. Динамические процессы в таких системах также зависят от числа элементов, от способа и величины связи между ними. В этих случаях отмечаются режимы бифуркаций, синфазной и противофазной синхронизации. С увеличением числа элементов в системе возрастает число режимов синхронизации. Если системы имеют пространственную структуру, то возможно образование взаимодействующих между собой синхронизированных кластеров. Такой тип взаимодействия называется глобальным. Синхронизация может охватить весь ансамбль элементов или только отдельные его области. Коллективная сила ансамбля осциллирующих элементов формируется в зависимости от внешнего воздействия и представляет собой аналог самоорганизации в сложных системах [5]. При этом доминирующий элемент становится ядром кластера. Согласно теории нелинейной динамики сложных систем [1], в ансамблях глобально связанных элементов (осцилляторов) на каждый элемент действует сила, пропорциональная средневзвешенному воздействию от всех элементов системы.

Цель, задачи и метод исследований. Цель данной работы – исследовать особенности синхронизации в больших сетях взаимосвязанных осцилляторов.

В задачи входит оценка зависимости скорости синхронизации от размерности модели (числа осцилляторов), оценка влияния на процесс синхронизации разброса начальных значений частоты, фазы и амплитуды, а также оценка влияния устранения части взаимосвязей между осцилляторами.

Метод исследования основан на численных экспериментах с компьютерной моделью осцилляторной сети на базе созданной для этой цели программы. Программа разработана на языке программирования С++ в компиляторе "Borland C++ Builder".

Как указывалось во введении, простые модели взаимодействующих осцилляторов на сегодня достаточно хорошо исследованы. Поэтому, учитывая ограниченный объем статьи, сосредоточимся на экспериментах со сложными осцилляторными сетями.

Программа, разработанная для проведения исследований, изображена на рисунке 1. В проводимых экспериментах по особенностям синхронизации использовались сети размером от 10 до 1000 осцилляторов.

На верхнем графике главной формы программы (см. рис. 1) отображены колебания осцилляторов в процессе синхронизации, а справа сверху номера осцилляторов, выводимых на график. Чтобы не перегружать отображение, одновременно выводятся кривые лишь для шести произвольно выбираемых осцилляторов. Ниже расположены радиокнопки переключения режимов "Осцилляторы" (кривые колебаний осцилляторов) и "Сигналы" (интерференция колебаний сигналов). Под ними таблица "Осцилляторы", позволяющая ввести произвольные номера осцилляторов, выводимых на график.

В нижней части главной формы программы расположены графики "Оценка" (качество синхронизации) и "Фазовый портрет", отображающий динамику произвольно выбираемой экспериментатором пары осцилляторов.

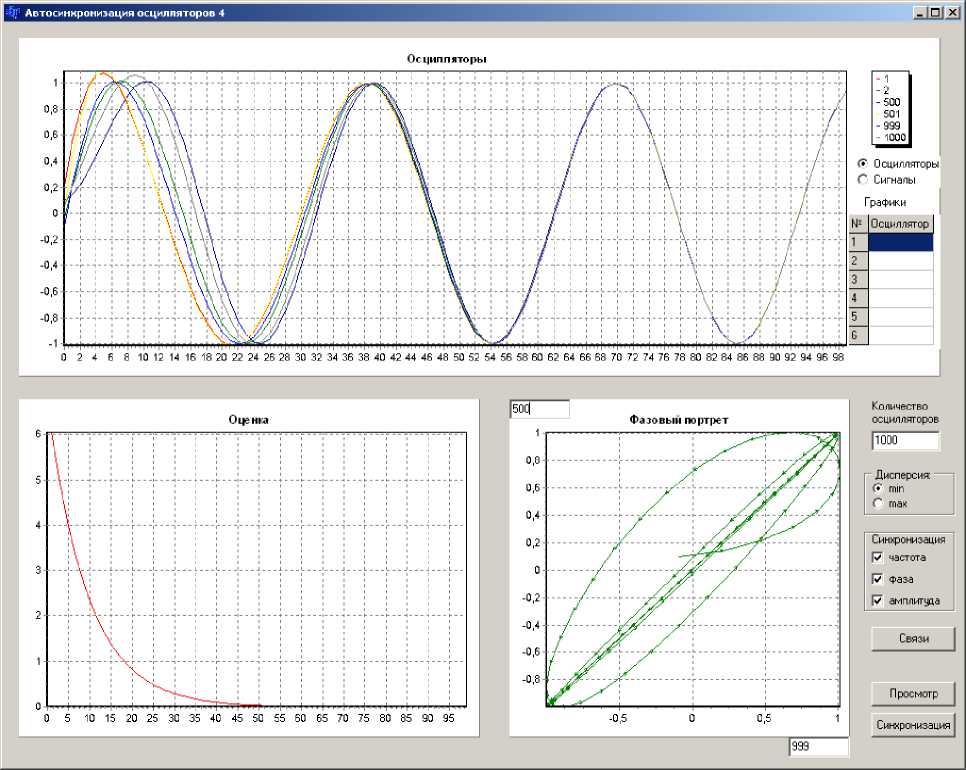
Рис. 1. Внешний вид главной формы программы

На панели управления программой (справа) можно указать "Количество осцилляторов", участвующих в численном эксперименте. Ниже расположена панель выбора начального состояния системы – разброса колебаний по частоте, фазе и амплитуде "Дисперсия". А под ней расположена панель, позволяющая выбрать, для каких параметров выполняется "Синхронизация". Кнопка "Связи" позволяет вывести форму "Свя- зи между осцилляторами", приведенную на рисунке 2 и предоставляющую возможность автоматического и произвольного выбора конфигурации взаимосвязей в системе. Кнопка "Просмотр" предназначена для отображения начального состояния системы, а кнопка "Синхронизация" запускает процесс синхронизации осцилляторов в выбранной экспериментатором конфигурации.

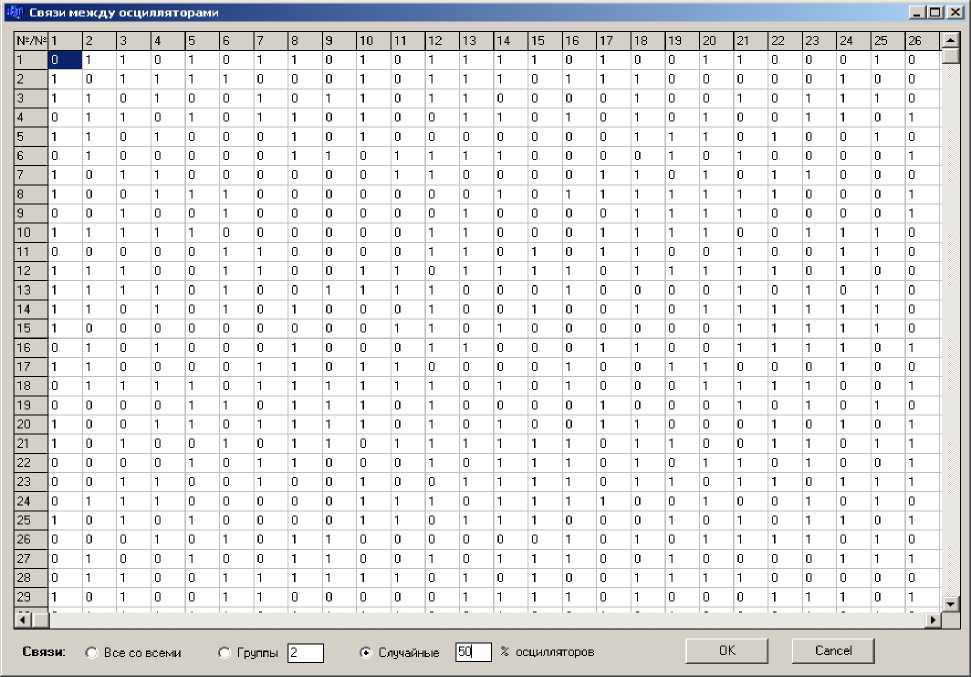
Рис. 2. Матрица взаимосвязей в системе осцилляторов

Результаты исследований1.    Синхронизация в сложных полносвязных сетях осцилляторов

Полносвязные сети осцилляторов представляют собой систему взаимодействующих осцилляторов, в которой каждый осциллятор связан со всеми остальными осцилляторами сети. Осцилляторы модели функционировали в дискретном времени в соответствии с формулой

Уг,t = Ai sin W + ^i ),

где i – номер осциллятора в сети;

• t – дискретное время;

• A – амплитудный множитель;

• ω – круговая частота;

• φ – фаза.

Как указывалось во введении, на каждый элемент (осциллятор) действует сила, пропорциональная средневзвешенному воздействию от всех элементов системы. Следовательно, ошибки синхронизации могут быть вычислены как

1     N - 1                       1     N - 1                      1     N - 1

• aw = :^ТЛ ^W-W '''   \ \ £^j~^ ^A‘=1П £Aj-Ai,

• j , * j                                        / , i * j                                      j , i * j

где N – число осцилляторов, воздействующих на текущий осциллятор i.

Синхронизация осуществляется путем смещения подстраиваемых параметров осцилляторов к средневзвешенным значениям:

Щ = Щ + ЛЩ A, p* = ^ + к^A, A = Ai + AAiA,

где звездочкой * обозначается новое значение подстраиваемого параметра;

λ – шаг модификации параметра.

Оценка синхронизации всей сети взаимодействующих осцилляторов:

H = 1 D^w +W ^{+Л А} 2 ^).

i

• Пример исходного состояния системы приведен на рисунке 3.

2. Синхронизация в сложных сетях осцилляторов с неоднородной структурой случайных связей

Процесс синхронизации осцилляторов в полносвязной сети не выявил специфических особенностей, зависящих от числа взаимодействующих осцилляторов. При изменении их числа от 10 до 1000 вид графика "Оценка" качества синхронизации практически не изменялся по форме и длительности установления минимальной оценки (соответствующей минимальной ошибке) во времени (см. рис. 1, нижний левый график).

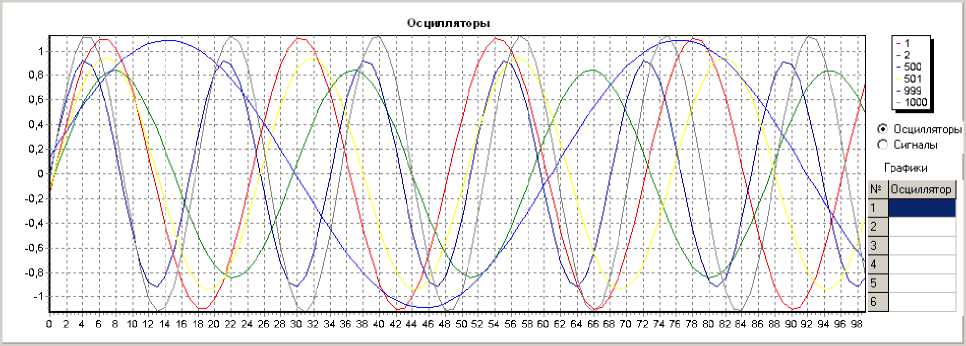
Рис. 3. Пример исходного состояния системы взаимосвязанных осцилляторов до начала синхронизации

Вместе с тем, с ростом дисперсии начальных значений подстраиваемых параметров осцилляторов наблюдалось изменение динамики режима синхронизации (рис. 4).

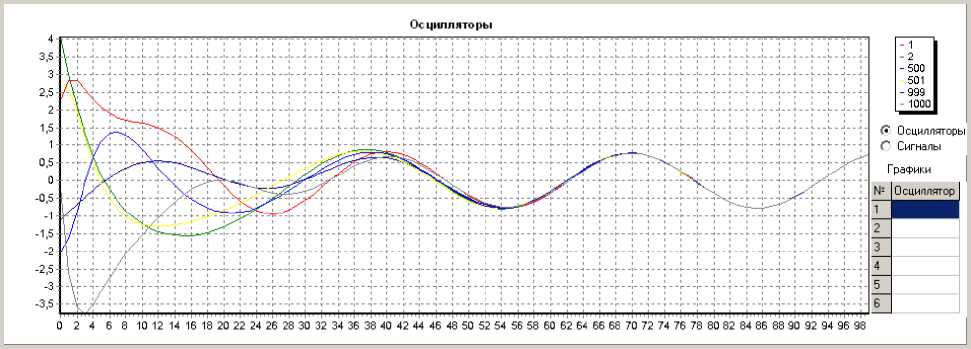
Рис. 4. Пример синхронизации с высокой дисперсией начальных значений параметров осцилляторов

Установка способа и плотности взаимосвязей в сети осцилляторов заданного размера производилась на форме (см. рис. 2), вызываемой по кнопке "Связи" на главной форме (см. рис. 1).

В предыдущем разделе рассматривались эксперименты с полносвязными сетями осцилляторов, генерируемыми при положении радиокнопки "Все со всеми". В данном разделе исследовались сети с частично удаленными связями. Радиокнопка "Группы" позволяла выделить несколько одинаковых групп осцилляторов, а радиокнопка "Случайные" сохраняла заданный процент связей между осцилляторами сети. При этом самопроизвольно формировалось различное число групп осцилляторов с различной степенью связанности.

Разбиение сети взаимосвязанных осцилляторов на группы приводило к частичной изоляции этих групп (кластеров) друг от друга. При однородных связях степень взаимодействия групп осцилляторов при синхронизации оказывалась пропорциональной плотности связей между осцилляторами взаимодействующих групп. Если полная синхронизация достигалась при взаимосвязях всех осцилляторов друг с другом, то синхронизация частично связанных групп приобретала более сложный характер (рис. 5).

Наибольший интерес представляют неоднородные сети осцилляторов как наименее исследованные и близкие к природным и сложным техническим системам. Однако в силу сложности взаимодействий множества кластеров в большой неоднородной сети, точное соотношение степени синхронизации с числом связей между элементами кластеров не представляется возможным. Однозначно выделялись различные частоты и фазы внутри слабо связанных кластеров. Пограничные элементы между кластерами синхронизировались либо с кластером, имеющим с ними наибольшее число связей, либо смещались в промежуточное состояние, не синхронизируясь ни с одним из взаимодействующих кластеров. Большое разнообразие способов синхронизации неоднородных осцилляторных сетей требует дальнейших исследований для изучения их свойств.

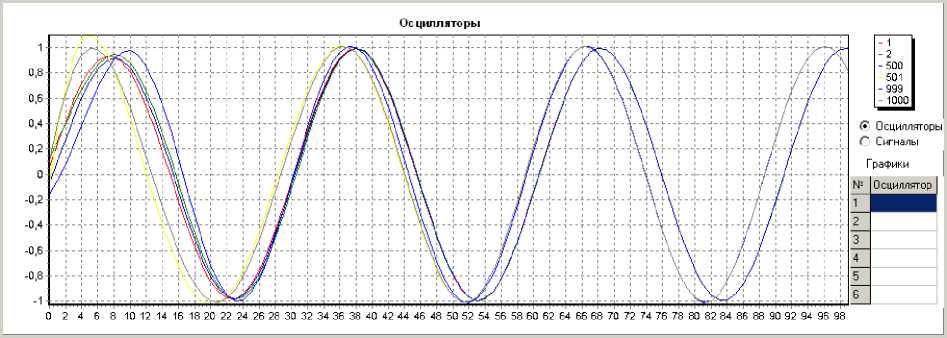
Рис. 5. Пример различия синхронизации осцилляторов в двух соседних кластерах для неоднородной сети

Заключение

Проведенные исследования продемонстрировали возможность эффективной синхронизации больших сетей взаимосвязанных осцилляторов.

Моделирование полносвязных и разряженных сетей с числом осцилляторов от 10 до 1000 показало, что скорость синхронизации слабо зависит от размерности модели (числа осцилляторов).

Разброс начальных значений частоты, фазы и амплитуды в сетях осцилляторов не оказывает значительного влияния на качество синхронизации.

С ослаблением взаимосвязей (ростом взаимной изолированности осцилляторов) качество синхронизации падает.

На примере разряженных сетей со случайными связями показано, что в областях с более плотными связями возникают кластеры синхронизированных между собой осцилляторов. Слабо взаимодействующие кластеры синхронизируются независимо друг от друга. Степень корреляции между кластерами при синхронизации осцилляторов возрастает с ростом числа взаимосвязей. "Пограничные" осцилляторы, через которые происходит взаимодействие между кластерами, в зависимости от соотношения размеров кластеров и числа связей этих осцилляторов в каждом из кластеров, могут синхронизироваться с одним из кластеров, либо занимать промежуточные состояния.