Автоволновые структуры во внешней флуктуирующей среде
Автор: Курушина С.Е., Иванов А.А., Желнов Ю.В., Завершинский И.П., Максимов В.В.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Физика и электроника
Статья в выпуске: 4-1 т.12, 2010 года.
Бесплатный доступ
Исследовано влияние мультипликативных флуктуаций параметров системы на образование диссипативных структур. Для структур Тьюринга получена система уравнений, описывающих взаимодействие незатухающих мод (параметров порядка) при возникновении неустойчивости типа мягкой моды. Показано, что флуктуации параметров приводят к изменению собственных значений неустойчивых мод системы и параметрическому возбуждению системы. Проведено численное моделирование эволюции пространственных структур. Исследованы изменения уровней флуктуаций распределений динамических переменных в процессе формирования пространственных диссипативных структур при изменении параметров внешнего случайного поля. Проведено численное моделирование эволюции спиральных волн и сложных автоволновых структур в поле внешних флуктуаций. Исследованы траектории дрейфа кончика спиральной волны.
Мультипликативные флуктуации параметров, формирование автоволновых структур, неустойчивые моды, уравнения гинзбурга-ландау, численное моделирование
Короткий адрес: https://sciup.org/148205492
IDR: 148205492 | УДК: 517.957,
Текст научной статьи Автоволновые структуры во внешней флуктуирующей среде
Возникновение и эволюция пространственных и пространственно-временных структур в экологических системах вызывают в настоящее время все возрастающий интерес [1-9].
Недавно были опубликованы работы, в которых исследуется образование пространственно-временных структур в системах хищник – жертва, находящихся во внешней флуктуирующей среде [3-5]. В работе [3] показано, что внешний шум разрушает симметрию и способствует “размыванию” контуров спиральных волн и тьюринговых структур, что, по мнению авторов [3], делает моделируемые структуры более адекватными естественным. Кроме того, показано, что в случае тьюринговых структур шум может индуцировать переходы между альтернативными стабильными пространственными структурами. В работах [4,5] рассматривается влияние дельта - коррелированного в пространстве и во времени внешнего случайного поля на динамику системы фитопланктон-зоопланктон с лизогенной вирусной инфекцией в популяции фито-
планктона. Показано, что внешний шум может способствовать выживанию и пространственному распространению восприимчивых и инфицированных видов, которые в детерминированной среде исчезают, а также индуцировать локальные вспышки “подверженных опасности” видов в случае, когда области параметров соответствуют неустойчивому состоянию системы. Этот эффект аналогичен шумоиндуцированному кинетическому переходу [10,11]. В [4,5] также исследуется эволюция концентрических и спиральных волн.
В настоящей работе внимание фокусируется на исследовании влияния внешней флуктуирующей среды на возникновение и формирование пространственных и пространственно-временных диссипативных структур (ДС) взаимодействующих популяций в модели Шеффера [12], описывающей динамику системы хищник-жертва для популяций фитопланктона и зоопланктона.
-
2. МОДЕЛЬ
Взаимодействие популяций фитопланктона x1 и зоопланктона x2 определяется системой уравнений [6,12]:
-
дx ax2
— = rx 1 (1 - x 1 ) - -—— x 2 + d 1 V x i ;
d t 1 + bx 1
dx2 axA g2 x2 r
-
2 = x7 - mx7 2 f + d V x ?.
d t 1 + bx1 2 2 1 + h2 x 2 22
где параметры r, a, b, m, g, h, f, d1 и d2 подробно описаны в [6,12]. Параметр f определяет посто- янную численность планктоноядной рыбы и является контрольным параметром. Локальная динамика и бифуркационный анализ системы (1) проведены в работах [2,6,9,12-14]. Вводя безразмерные время τ= rt и координаты x' = x-Jr I di и представляя параметры m/rи a/ r, зависящие от коэффициентов естественного прироста фитопланктона r, естественной смертности зоопланктона m и трофического коэффициента a, в виде: m I r = (m0 I r0)(1 + f[(x', t)) , a I r = (a о I ro )(1 + f2 (x , t)), где m0, r0, a0 - пространственно-временные средние соответствующих коэффициентов, перепишем уравнения модели (1) следующим образом:
lx1 = xi(1 - xi) -∂τ
- a0 (1 + f2( xT ))
r0 (1 + bx 1)
+ V' 2 xx;
5 x 2 ∂ τ
a 0 (1 + f 2 ( X ' T )) r o
x 1 x 2
(1 + bx 1 )
-
- m- (1 + f( x , T )) x 2 - r o
-
g x 2 r 0(1 + h 2 x 2 )
f + d 2 V' 2 x 2.
d 1 2
Здесь случайные однородные изотропные поля fi ( x , t ) определяют пространственно-временные гауссовы флуктуации этих параметров.
-
3. ПРОСТРАНСТВЕННЫЕ СТРУКТУРЫ
-
3.1. Аналитическое исследование.Уравнения Гинзбурга-Ландау
-
Исследование системы (2) будем проводить, используя концепцию параметров порядка, развитую в [15].
Пусть поля fi( x ? ,ф) имеют корреляционный тензор f ( x', t) f j ( x "j^ = F ( x " - x " ) 8^-T ) 5 j ( ij= 1,2) и нулевые средние значения. Функции Fl (| x -x"| ) определяют пространственную зависимость корреляций однородных изотропных случайных полей [16,17]. Дельта - коррелированность во времени фактически означает, что время корреляции случайного поля гораздо меньше всех характерных времен задачи.
Перепишем систему (2) в операторном виде, выделяя линейную и нелинейную части. Нелинейный оператор представляет собой вектор, содержащий квадратичные и кубические слага- емые, полученные разложением в ряд детерминированных слагаемых в правой части (2), и вектор, содержащий случайные компоненты. Решение системы ищем в виде разложения в ряд по собственным функциям линейного оператора. После преобразований получаем систему уравнений для амплитуд. Проведя процедуру адиабатического исключения устойчивых мод, получаем уравнения Гинзбурга-Ландау для амплитуд неустойчивых мод:
Я£ (1)
-f- - А( k, f1 =∂τ
(1) (1) (1)
= A ^11 (ku , ku , ku fk"Sk"d(ku + ku - ku ) + kk ,uu
+ УХk,, k", k", k", kцУ 21 21 ^(k" + k"" + k" k) + u u u u s ku ku k u u u u u kkk"', uuu
+ A a( ku ’ kU ’ ks ’ zq (t ))fk1u) + k', u
+ A в(ku , ku , k'u , k, , Zq (t jfkui^kuI + k k ,uu
+ Ay(ku,k'u,ku,k,' k,, Zq(t)fkufkufkiu + kk k , uuu
+ f [ku , k, , Zq (t)].
Здесь функции «(ku,ku,ku',ku",k,) , a(ku, ku, k, , Zq (t)), e(ku, k'u,k'",k,,z (t)) , Y(k" , k" , k" , k", k, , Zq (t)) и f [k" , k, , Zq (t)] не приведены ввиду их крайней громоздкости. Выражения для них можно увидеть в Приложении к статье на сайте morfogenez/. δ-функции дают “правила отбора” для взаимодействующих мод.
Усредняя уравнения системы (3) по ансамблю реализаций, принимая во внимание ее формальные решения и раскрывая моменты и корреляторы на основании правил [18,19], окончательно получаем систему, структура которой имеет вид:
d f(1) \
В системе (4) возникают дополнительные слагаемые, входящие в оператор L 1 ( k u , k U , k U , k s ) и пропорциональные
^ k u (t )) , что приводит к изменению собственного числа каждой моды и, как следствие, к изменению области неустойчивости и смещению точки бифуркации Тьюринга.
Пусть значения интенсивностей флуктуаций θ j настолько малы, что в (4) можно ограничиться только членами, линейными по интенсивности шума. Выделим из L i ( k u , k U , k U , k s ) слагаемые, дающие вклад в собственное значение данной моды. В результате получим:
2 = ^ ( ku ) + 0 f ( x ( k u )/k 2f f + k f M k u )/( ku 2 + k 2f f)^ ) +
+ 0X(n(ku)/k211 + kfiP(ku)(ku2 + kfi)3/f). (5) 21(ku) — дисперсионное соотношение для линейной задачи (1). Функции х(ku) , M(ku ) , П(ku ) , P(ku ) здесь не приводятся в силу их громоздкости. Подробный вывод выражения (5) представлен в Приложении к статье на сайте При выводе выражения (5) учтено, что ^-k) = ^k(j) = ^kj), так как решения уравнений (5) должны быть действительными. Из выражения (5) для собственных значений λ неустойчивых мод видно, что их действительная часть пропорциональна интенсивностям флуктуаций 6j и зависит от радиусов корреляции rf = 1 / k fj. И как следствие, изменение инкремента нарастания каждой моды должно приводить к изменению скорости образования пространственных ДС в зависимости от параметров мультипликативного случайного поля. В работах [20,21] аналитически и численно для модели морфогенеза Гирера – Майнхардта и в [22] численно для моде- ли распределенного брюсселятора показано, что внешний шум приводит к аналогичному явлению.
Результаты численных расчетов выражения (5) представлены на рис. 1. Из рис. 1а видно, что в закритической области при увеличении интенсивности флуктуаций θ 1 поля f1( x ' , τ ) , входящего в линейную компоненту системы (2), область неустойчивых мод, для которых Re λ >0 , увеличивается. Кроме того, Re λ больше Re λ 1(ku) ( θ 1= θ 2=0) по абсолютному значению. Следовательно, при наличии мультипликативного шума амплитуды неустойчивых мод нарастают значительно быстрее, чем в его отсутствии, что ускоряет процесс разрушения однородного состояния и образования ДС. Расчеты показывают, что увеличение интенсивности θ 2 поля f2( x ' , τ ) , входящего в нелинейную компоненту системы (2), влияет на этот процесс значительно сильнее.
На рис. 1б приведены зависимости Re λ (k) в докритической области. Пунктирной линией показана соответствующая зависимость при отсутствии флуктуаций. Видно, что Re λ 1(ku) < 0 и неустойчивость не возникает. При наличии флуктуаций (линии сплошная и пунктирная с точкой на рис.1б) возникает область неустойчивых мод, т.е. шум индуцирует параметрическую неустойчивость системы (2).
Разрыв второго рода в зависимости Re λ (k) обусловлен выбором компонент собственных векторов сопряженного оператора и не влияет на вышеприведенный анализ.
-
3.2. Численное моделирование
Моделирование системы (2) проводилось при помощи метода Кранка-Николсона [23]. Моделирование случайного поля осуществлялось с использованием математического пакета MatLab.
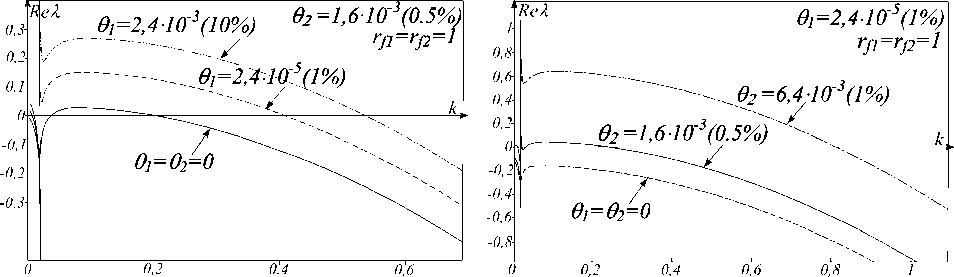
а) б)
Рис. 1. Характерные зависимости действительных частей собственных значений Re λ от волновых чисел k:
а – в закритической области вдали от точки бифуркации Тьюринга при изменении θ 1, θ 2 =1,6·10-3; б – в докритической области при изменении θ 2, θ 1 =2,4·10-5.
Для сравнения значений Re λ на рисунках приведены кривые Re λ 1(ku)( θ 1= θ 2=0)
В нашей работе для моделирования выбран следующий ряд параметров, обеспечивающих появление неустойчивости типа мягкой моды [3]: m0 / r0=м1 = 0,49; a0/ r0=м2 = 8; g2/r0 = 2,056; f = 0,093; h =0,857; b = 11,905; d1/d2 = 1000 и периодические граничные условия. Область интегрирования квадратная: l1=l2 =200. Начальные условия соответствуют однородному стационарному состоянию системы, т.е. моделируется спонтанное образование структур без начального возмущения.
Так как δ-коррелированный шум является идеализацией, реальная флуктуирующая среда моделируется как однородное изотропное гауссово поле с корреляционным тензором (f!(X,T)fj («t) = 9 exP-kf x - x) exp-ktik'-^ )5j Обоснование такого выбора модели флуктуирующего окружения приводится в работе [24]. Случайные изменения внешней среды обусловлены суммарным действием множества слабосвязанных факторов и происходят значительно быстрее, чем заметные изменения в поведении системы. Поэтому времена корреляции случайного поля выбраны значительно меньшими, чем характерные времена системы (1). Величины kti , обратные временам корреляции, при моделиро- вании являются фиксированными и равными 100 для всех численных экспериментов. Такой выбор величин kti позволяет провести качественное сравнение аналитических выводов, сделанных в разделе 3.1, с результатами численного эксперимента.
Также отметим следующее. Так как флуктуации параметров вызваны случайными изменениями внешней среды, разумно предположить, что среднеквадратичные отклонения параметров 5 ( E j ) ( e j = ц ^ , ^ 2 ) должны определяться по отношению к их пространственно-временным средним E j , то есть ( 5 ( e j )/ E j ) - 100% = nE . Тогда интенсивность флуктуаций определяется выражением 9 j = S\E j ) . Диапазоны изменения интенсивностей мультипликативного шума, рассматриваемого в работе, достаточно велики: 0 < 9 1 < 0,049 , что соответствует изменению Пц 1 от 0 до 45% и 0 < 9 2 < 1,44 , что соответствует изменению Пм 2 от 0 до 15%.
Процесс формирования пространственных ДС в распределении плотности биомассы фитопланктона при увеличении интенсивности флуктуаций θ 1 параметра m0/r0 от нуля до 0,049 ( П ^ 1 =45%) при неизменном и 2 представлен на рис. 2. Кроме обычной картины распределения
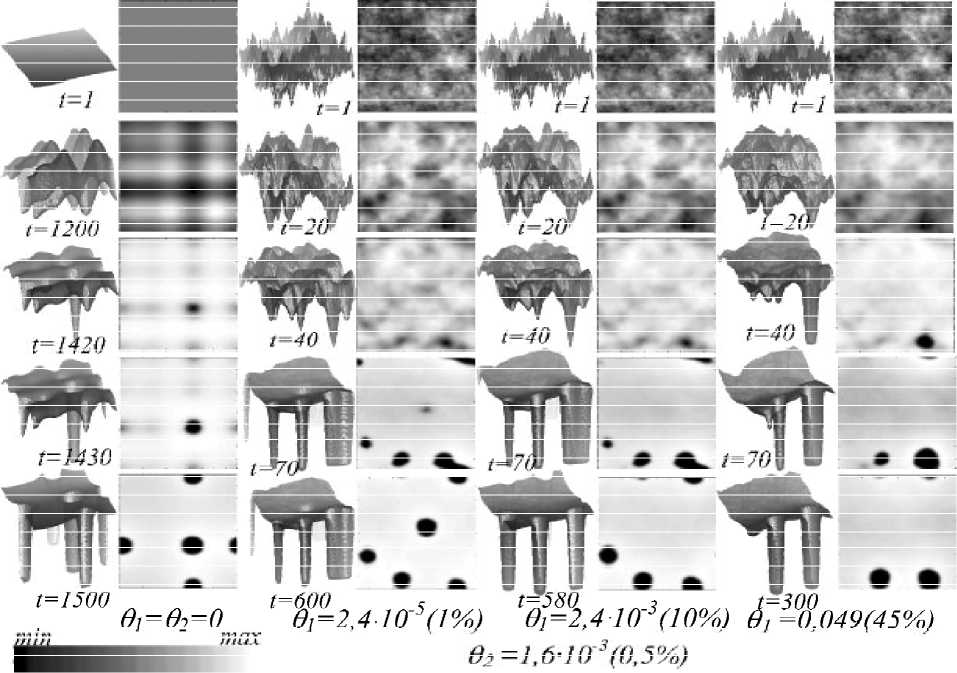
Рис. 2. Формирование тьюринговых структур в распределении фитопланктона при увеличении интенсивности флуктуаций θ 1 параметра m/r (см. пояснения к рисунку в тексте) В середине указаны моменты модельного времени. Нижний ряд соответствует моментам установления статистически стационарного состояния при разных значениях θ 1 и θ 2 = 1,6·10-3. kf1 = kf2 = 1
плотности биомассы фитопланктона по поверхности на этих рисунках добавлено соответствующее изображение сверху, дающее более наглядное представление о конфигурации ДС. Градиент цвета от черного к белому визуализирует изменение значений переменной от минимального до максимального соответственно. Черные области соответствуют пустым участкам пространства.
Первая пара вертикальных рядов демонстрирует спонтанное возникновение симметричной структуры Тьюринга в отсутствии флуктуаций. Вторая, третья и четвертая пары вертикальных рядов иллюстрируют образование структур при интенсивностях 0 1 , равных 2,40140 -5 ,2,40140 -3 и 0,049 (одно-, десяти – и 45-процентная степень зашумления параметра m0/r0 ), соответственно. При этом 0 2 =1,640-3.
Из рис. 2 видно, что при увеличении 0 1 процесс разрушения однородного состояния и формирования статистически стационарной ДС происходит быстрее, чем в отсутствии шума, что качественно соответствует теоретическим выводам, сделанным выше. Также видно, что наличие внешних флуктуаций разрушает симметрию пространственных структур.
Численно исследовался вопрос об изменении уровня флуктуаций распределения плотностей биомасс планктона при переходе системы от однородного состояния к ДС в описанном выше эксперименте. На рис. 3 приведены усредненные по поверхности слоя флуктуации плотности био- массы с=Ц
Увеличение 0 2 до 0,16 при неизменном и 1 приводит к аналогичному эффекту, однако теперь этот процесс идет интенсивнее, чем в вышеописанном эксперименте.
Видео-файлы эволюции системы (2) представлены на сайте morfogenez/.
-
3.3. Параметрическое возбуждение солитоноподобных структур
В разделе 3.1 аналитически показано, что шум индуцирует параметрическую неустойчивость системы (2). Для моделирования эволюции системы (2) в докритической области выбраны следующие параметры: m0 / r0= 0,51; a0/ r0= 8; g2/r0 = =2,056; f = 0,093; h =0,857; b = 11,905; d1/d2 = 1000; 0 1 = 2,640-3 , 0 2 =2,5640-2; kf1 = kf2 = 0,5; 1 1 =1 2 =200 и периодические граничные условия.
На рис. 4 представлена эволюция распределения плотности биомассы фитопланктона для моментов времени t = 1, 927, 940, 950 и 1120.
Графики зависимостей действительных частей собственных значений неустойчивых мод от
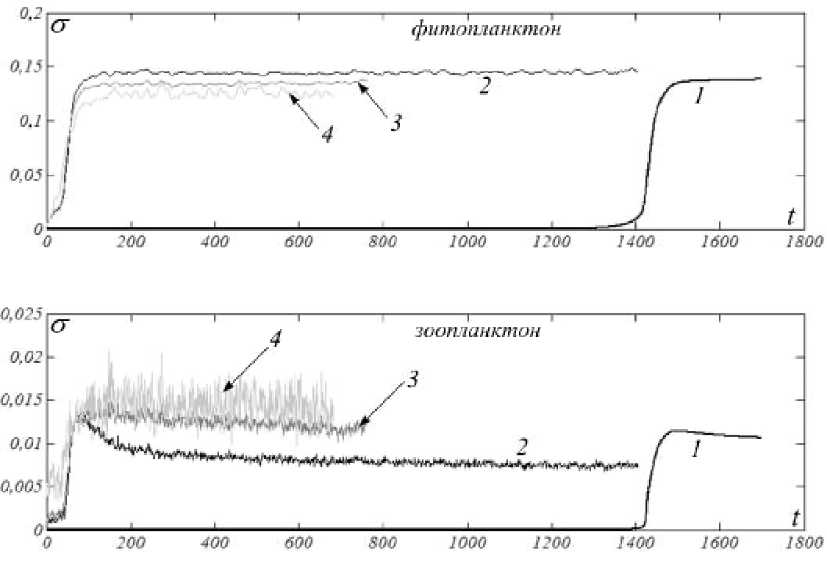
Рис. 3 Зависимости от времени усредненных по поверхности слоя флуктуаций плотности биомассы фитопланктона и зоопланктона. k 1 = к 2 = 1. 1: 0 1 = и=0. 2: 0 1 = 2,40140-5 , 0 2 = 1,640-3. 3: 0 1 = 2.401-10 - 3 , 0 2 = 1,6^10-3. 4: 0 1 = 0,049 , 0 2 = 1,6-10-3.

Рис. 4. Формирование ДС при параметрическом возбуждении в докритической области
волнового числа, полученные на основании выражения (5), а также графики усредненных по поверхности слоя флуктуаций плотностей биомассы фитопланктона и зоопланктона, представлены на рис. 5 и 6, соответственно. На рис. 5 для сравнения изображена зависимость Re λ 1(ku) (сплошная линия) в отсутствии внешнего шума при тех же параметрах модели.
Как видно из рис. 5 (сплошная линия) при выбранных параметрах модели в отсутствии шума, действительная часть всех собственных значений отрицательна, т.е. неустойчивость отсутствует. Устойчивым решением является однородное распределение плотностей биомасс по поверхности слоя. При наличии внешнего шума (пунктирная линия на рис. 5) некоторые моды приобретают положительный инкремент. Таким образом, при выбранных параметрах моделирования, согласно выражению (5), возникает неустойчивость типа мягкой моды, вызванная флуктуациями параметров – параметрическая неустойчивость. Так как подобная неустойчивость возникает только при интенсивности внешнего шума больше некоторой критической, интенсив- ность внешнего шума является бифуркационным параметром системы (2). Как и при жестком возбуждении структур в докритической области, связанном с некоторым начальным возбуждением критической амплитуды, возникающая при параметрической неустойчивости ДС имеет солитоноподобный вид (см. рис. 4, t = 1120). Но физическая природа его происхождения иная.
Из графиков зависимостей средних по поверхности слоя флуктуаций (рис. 6) видно, что в случае параметрической неустойчивости в процессе образования уединенной ДС флуктуации возрастают скачком. Однако уровень флуктуаций при установившейся статистически стационарной ДС (см. значения σ после t= 1120 на рис. 6) значительно меньше, чем соответствующий уровень в закритической области (рис. 3).
Отметим также, что при разрушении однородного состояния наблюдаются всплески флуктуаций и в более ранние моменты времени, например при t = 520, 850 (рис. 6). Этим моментам соответствуют неудачные попытки установления ДС. Для момента t= 850 изображена такая возникающая коротко живущая структура.
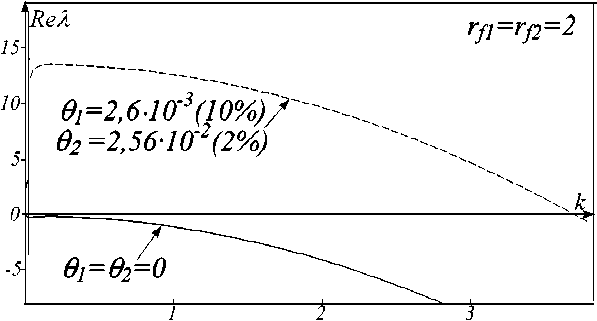
Рис. 5. Зависимости Re λ от k для выбранных параметров моделирования (см.текст) при параметрическом возбуждении (пунктирная линия) и в отсутствии внешнего шума (сплошная линия)
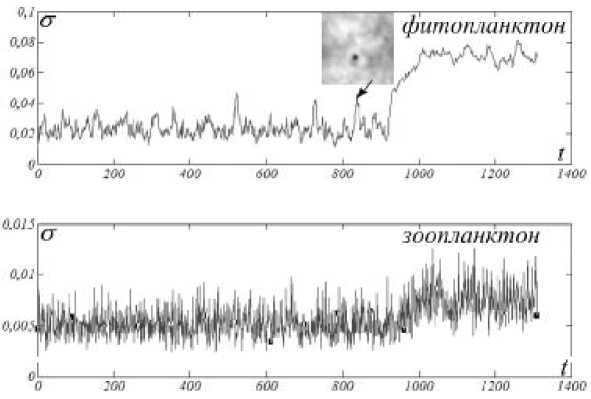
Рис. 6. Усредненные по поверхности слоя флуктуации динамических переменных при параметрическом возбуждении
Таким образом, результаты численного моделирования качественно полностью подтверждают теоретические выводы, сделанные в разделе 3.2.
-
4. СПИРАЛЬНЫЕ ВОЛНЫ И СЛОЖНЫЕ АВТОВОЛНОВЫЕ СТРУКТУРЫ
-
4.1. Спиральные волны
Некоторые моменты динамического поведения пространственно-временных структур, возникающих в системе (2), описаны в [2,3]. В данной работе исследуется влияние флуктуаций параметров системы на эволюцию спиральных волн и сложных автоволновых структур.
Для моделирования спиральных волн выбран следующий ряд параметров, обеспечивающих одновременное существование в системе (2) бифуркаций Хопфа и Тьюринга: m0 / r0= 0,6; a0/ r0= 5; g2/r0 = 100; f = 0,02; h =10; b = 5; d1/d2 = 1; l1=l2 =200
и беспотоковые граничные условия. Спиральные волны инициируются посредством пересечения полей распределения плотностей биомасс популяций с постоянным градиентом, возмущающих соответствующее стационарное состояние.
На рис. 7 представлен процесс формирования спирали и траектория дрейфа ее кончика (точки обрыва волнового фронта) в отсутствии шума. Для определения положения кончика спирали использовался метод, описанный в [25]. Положение кончика спиральной волны, аналогично [25], определялось как точка пересечения изолиний с уровнем 0,52 для фитопланктона и 0,24 для зоопланктона. Изолинии полей распределения планктона для указанных значений строились с использованием математического пакета MatLab. Кончик спирали совершает движение по эллиптической траектории, ориентация которой по отношению к некоторому выбранному направлению изменяется при каждом полном обороте (рис. 7, справа).
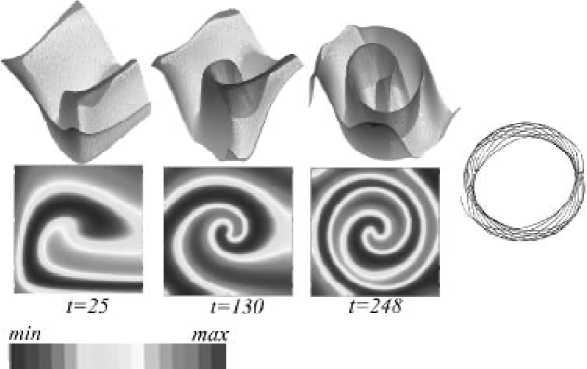
Рис. 7. Формирование спиральной волны и траектория дрейфа кончика спирали в отсутствии флуктуаций параметров

Рис. 8 Эволюция спиральных популяционных волн фитопланктона при увеличении интенсивности флуктуаций и2 . и1 = 3,6·10-5(1%). kf1 = kf2 = 1.
Эволюция популяционных спиральных волн фитопланктона в поле флуктуаций представлена на рис. 8. На нем изображено формирование спиралей при увеличении интенсивности флуктуаций θ 2 . Горизонтальные ряды соответствуют моментам t = 25, 130 и 348 единицам модельного времени. Четыре пары вертикальных рядов соответствуют разным значениям θ 2 при постоянной малой интенсивности θ 1 .
Из рис. 8 видно, что спиральные волны устойчивы к слабому внешнему флуктуационному фону (две пары вертикальных рядов слева на рис. 8), и, в отличие от тьюринговых структур, их конфигурация и скорость формирования не изменяется. Однако, даже при малых вешних флуктуациях наблюдается размывание и искажение контуров спирали. Тип поведения кончика не изменяется, но в его дрейфе возникают элементы случайности: флуктуирует как сама траектория, так и ее ориентация в пространстве (см. четвертый горизонтальный ряд рис. 8). Увеличение θ 1 при неизменном θ 2 приводит к аналогичному эффекту, только теперь этот процесс замедляется в сравнении с вышеописанным экспериментом.
При увеличении интенсивности флуктуаций внешнего случайного поля спиральная волна разрушается (пара вертикальных рядов справа на рис. 8).
-
4.2. Сложные автоволны
Интересным является вопрос об эволюции сложных автоволновых структур во внешнем случайном поле. Для моделирования пространственно-временной структуры были выбраны парамет- ры m0 /r0= 0,6; a0/ r0= 5; g2/r0 = 100; f = 0,02; h =10; b = 5; d1/d2 = 1; l1=l2=200 и периодические граничные условия. В качестве начальных условий взят небольшой локализованный в центре участок с однородным распределением плотности биомассы планктона. Рис. 9 демонстрирует эволюцию получающейся в результате сложной ав-товолновой структуры. Из локализованного участка образуется генератор концентрических волн (ведущий центр). Вследствие периодических граничных условий волновые фронты взаимодействуют, и образуется система из пяти ведущих центров и четырех ревербераторов. Колебания генератора концентрических волн, расположенного в центре, происходит в противофазе с четырьмя генераторами, расположенными ближе к границе. Возможность образования генератора концентрических волн из пары спиралей с противоположным направлением вращения описана в [26]. Далее с течением времени взаимное расположение элементов структуры изменяется. В результате все генераторы оказываются в центре образца, после чего конфигурация сложной автоволны устанавливается.
Воздействие шума на описываемую выше пространственно-временную структуру демонстрирует рис. 10. Видно, что шум полностью разрушает ее симметрию. В случайном поле с малой интенсивностью образуются сложные автоволны с различными конфигурациями, быстро сменяющие друг друга. При увеличении интенсивности внешних флуктуаций пространственно-временные структуры разрушаются. Поведение системы становится хаотическим.

Рис. 9. Эволюция сложной пространственно-временной структуры в отсутствии шума

Рис. 10. Изменение конфигурации автоволновой структуры, изображенной на рис. 12, во внешнем случайном поле. Изображены кадры, соответствующие моменту времени t =600
-
5. ЗАКЛЮЧЕНИЕ
Исследовано влияние мультипликативных флуктуаций параметров системы на образование диссипативных пространственных и пространственно-временных структур в системе реакция-диффузия. В качестве конкретной модели рассмотрена распределенная модель Шеффера, описывающая динамику взаимодействия фитопланктона, зоопланктона и планктоноядной рыбы.
Влияние шума на образование пространственных ДС изучено при возникновении неустойчивости типа мягкой моды. С точностью до слагаемых, линейных по интенсивностям флуктуаций и кубических по амплитудам неустойчивых мод, получены уравнения Гинзбурга-Ландау, описывающие взаимодействие параметров порядка. Показано, что мультипликативные флуктуации параметров системы приводят к изменению собственных значений задачи, и как следствие, изменению области неустойчивости системы и скорости образования ДС, а также параметрическому возбуждению системы. Проведено численное моделирование эволюции тьюринговых структур. Продемонстрировано качественное соответствие между теоретическими вы- водами и численным экспериментом. Исследовано изменение уровня флуктуаций динамических переменных в процессе формирования ДС при изменении параметров внешнего случайного поля.
Проведено численное моделирование эволюции спиральных волн и сложных автоволновых структур в поле внешних флуктуаций. Исследованы траектории дрейфа кончика спиральной волны. Показано, что спиральные волны устойчивы к слабому внешнему флуктуационному фону, однако при этом происходит размывание контуров спирали и в дрейфе ее кончика возникают элементы случайности: флуктуирует как сама траектория, так и ее ориентация в пространстве. Моделирование эволюции сложных автоволновых структур показало, что слабый шум разрушает их симметрию.
Рассмотренная модель является моделью типа реакция-диффузия, поэтому подобного влияния внешнего случайного поля на формирования ДС следует ожидать и в других системах данного типа.
Работа частично поддержана аналитической ведомственной целевой программой “Развитие научного потенциала высшей школы” (20092010 гг.), грант 2.1.1/309.
Список литературы Автоволновые структуры во внешней флуктуирующей среде
- Spatiotemporal complexity of plankton and fish dynamics/Medvinsky A.B., Petrovskii S.V., Tikhonova I.A., Malchow H., Li Bai Lian//SIAM Review. 2002. №44. P.311-370.
- Emergence of spatiotemporal chaos driven by far field breakup of spiral waves in the plankton ecological systems/Liu Quan Xing, Sun Gui Quan, Li Bai Lian, Jin Zhen. URL: http://arxiv.org/abs/0704.0322 (дата обращения 15.02.2010)
- Malchow H., Hilker F.M., Petrovskii S.V. Noise and productivity dependence of spatiotemporal pattern formation in a prey predator system//Discrete and continuous dynamical systems. Ser. B. 2004. Vol.4. №3. P.705-711.
- Spatiotemporal patterns in an excitable plankton system with lysogenic viral infection/Malchow H., Hilker F.M., Sarkar R.R., Brauer K.//Mathematical and Computer Modelling. 2005. Vol.42. P.1035-1048.
- Oscillations and waves in a virally infected plankton system. Part I: the lysogenic stage/Malchow H., Hilker F.M., Petrovskii S.V., Brauer K.//Ecological Complexity. 2004. Vol.1. P. 211-223.
- Malchow H. Motional instabilities in prey predator systems//J. Theor. Biol, 2000, v.204, p.639-647.
- Garvie M.R., Trenchea C. Analysis of two generic spatially extended predator prey models//Preprint submitted to Elsevier Science. 2006. 16 p.
- Baurmann M., Gross Th., Feudel U. Instabilities in spatially extended predator prey systems: spatio temporal patterns in the neighborhood of Turing Hopf bifurcation//Preprint submitted to Journal of Theoretical Biology. 2006. 18p.
- Malchow H. Spatiotemporal pattern formation in nonlinear non equilibrium plankton dynamics//Procc. R. Soc. Lond. B. 1993. 251:103.
- Михайлов А.С., Упоров И.В. Критические явления в средах с размножением, распадом и диффузией//УФН. 1984. Т.144. В.1. C.79-114.
- Курушина С.Е., Максимов В.В. Шумоиндуцированные фазовые переходы в процессах конкуренции во флуктуирующих средах//Известия вузов. Прикладная нелинейная динамика. 2010. №1. С. 88-101.
- Scheffer M. Fish and nutrients interplay determines algal biomass: a minimal model//OIKOS. 1991. №62. P. 271-282.
- Satnoianu R.A., Menzinger M. Non Turing stationary patterns in flow distributed oscillators with general diffusion and flow rates//Phys. Rev. E. 2000, Vol. 62(1), P.113-119.
- Satnoianu R.A., Menzinger M., Maini P.K. Turing instabilities in general systems//J. Math. Biol. 2000. №41. P.493-512.
- Хакен Г. Синергетика. М.: Мир, 1980. 406 с.
- Ахманов С.А., Дьяков Ю.Е., Чиркин А.С. Введение в статистическую радиофизику и оптику. М.: Наука, 1981. 640 с.
- Рытов С.М. Введение в статистическую радиофизику. М.: Наука. 1966, 404 с.
- Кляцкин В.И. Стохастические уравнения глазами физика. М.:, Физматлит, 2001, 528 с.
- Стратонович Р.Л. Нелинейная неравновесная термодинамика. М.: Наука, 1985. 480 с.
- Курушина С.Е. Аналитическое исследование и численное моделирование контрастных диссипативных структур в поле флуктуаций динамических переменных.//Известия вузов. Прикладная нелинейная динамика. 2009, №6, с. 125-138.
- Курушина С.Е., Иванов А.А. Диссипативные структуры в системе реакция диффузия в поле мультипликативных флуктуаций//Известия вузов. Прикладная нелинейная динамика. 2010. №3.
- Асташкина Е.В., Романовский Ю.М. Флуктуации в процессе самоорганизации//Математические модели в экологии. Горький: Изд-во Горьковского ун-та. 1980. С. 74-82.
- Методы анализа нелинейных динамических моделей/Холодниок М., Клич А., Кубичек М., Марек М. М.: Мир, 1991. 368 с.
- Хорстхемке В., Лефевр Р. Индуцированные шумом переходы: теория и применение. М.: Мир, 1987, 400 с.
- Елькин Ю.Е., Москаленко А.В., Стармер Ч.Ф. Спонтанная остановка дрейфа спиральной волны в однородной возбудимой среде//Математическая биология и биоинформатика. 2007. Т. 2. №1. С. 73-81.
- Петров И.Б., Полежаев А.А., Шестаков А.С. Волновые процессы в нелинейных активных средах//Математическое моделирование. 2000. Т.12. № 1. С. 38-44.


