Азотирование в электростатическом поле при восстановлении изношенных деталей сельскохозяйственной техники (на примере распределителей аксиально-поршневых насосов, гидромоторов)
Автор: Агафонов С.В.
Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau
Рубрика: Техника
Статья в выпуске: 9, 2012 года.
Бесплатный доступ
На основании проведенного математического моделирования и практических исследований определены оптимальные параметры процесса азотирования размерновосстановленных распределителей аксиально-поршневых насосов (гидромоторов), изготовленных из стали 38Х2МЮА.
Детали, химико-термическая обработка, азотирование, математическое моделирование, гибридный регрессионный комплекс
Короткий адрес: https://sciup.org/14082620
IDR: 14082620 | УДК: 621.785.532
Текст научной статьи Азотирование в электростатическом поле при восстановлении изношенных деталей сельскохозяйственной техники (на примере распределителей аксиально-поршневых насосов, гидромоторов)
В настоящее время имеются различные эффективные способы повышения долговечности деталей машин. Одним из наиболее эффективных и широко применяемых методов повышения долговечности многих ответственных деталей является их термическая и химико-термическая обработка (ХТО). ХТО воздействует на поверхностные слои металла, в которых концентрируются максимальные напряжения, возникают трещины, развиваются процессы износа и коррозии.
Химико-термическая обработка сочетает термическое и химико-термическое воздействия с целью изменения химического состава, структуры и свойств поверхностного слоя металла или сплава. Для повышения долговечности наиболее ответственных деталей машин широко используются процессы цементации, нитроцементации и азотирования. Примером могут служить детали автомобилей, тракторов, станков, сельскохозяйственных и других машин.
Азотирование относится к числу наиболее эффективных методов ХТО, повышающих поверхностную твердость, прочность, износостойкость и коррозионную стойкость стальных изделий. Основным недостатком процесса азотирования является большая длительность технологического цикла.
Цель исследований. Разработка эффективного ресурсосберегающего технологического процесса азотирования в электростатическом поле при восстановлении изношенных деталей сельскохозяйственной техники, позволяющего получать на поверхности заданные эксплуатационные свойства.
На основании рассмотренных работ, проведенного библиографического анализа по различным видам химико-термической обработки и в соответствии с поставленной целью определены задачи исследований :
-
1. Разработать программный комплекс для осуществления моделирования режимов азотирования в электростатическом поле.
-
2. Определить оптимальные по энергоматериальным затратам технологические, электрические и газодинамические параметры процесса азотирования в электростатическом поле.
Разработка линейной регрессионной математической модели оптимальных режимов азотирования в электростатическом поле проводилась на базе опытов с цилиндрическими образцами диаметром 12 мм, изготовленных из стали 38Х2МЮА. При решении данной задачи (первого этапа) в качестве переменных были выбраны пять основных факторов, наиболее полно характеризующих процесс формирования азотированного слоя:
-
• х 1 - степень диссоциации аммиака, %;
-
• х 2 - температура процесса, °С;
-
• х 3 - длительность процесса, ч;
-
• х 4 - напряжение на электродах, В;
-
• х 5 - знак потенциала на образце.
Параметрами оптимизации служили:
-
• у 1 - поверхностная твердость по Виккерсу, HV;
-
• у 2 - износостойкость, мг/см2;
-
• у 3 - глубина азотированного слоя, мм.
По результатам опытов были рассчитаны коэффициенты уравнений линейной регрессии отдельно для каждого параметра оптимизации и проведена их статистическая обработка, получена обобщенная линейная модель процесса азотирования в электростатическом поле [1]:
y = d = 0,517 - 0,012 x 1 + 0,147 x 2 + 0,075 x 3 + 0,025 x 4 - 0,005 x 5 . (1)
Для точного расчета оптимального режима азотирования был проведен второй этап апостериорного математического моделирования на базе нелинейных уравнений регрессии, при этом компьютерное моделирование данного этапа исследований и численные расчеты проводились в специальной программной среде «ГРЕК» - гибридный регрессионный комплекс, разработанной с участием автора [2].
Методологически второй этап состоял в следующем: проанализировав данные математического моделирования первого этапа, уравнение модели линейной регрессии, было расширено до векторноматричного линейно-квадратичного уравнения вида [3]:
y ( u )= c + Au +diag [ u T B 1 u ,…, u TB 3 u ]col(1,…,1)+ ε ( u ), (2)
или (после идентификации) в координатной форме:
y 1 ( u )=97,4-65,075 u 1 -3,706 u 2 +9,369 u 3 +5,991 u 4 --64,313 u 1 2+
+25,339 u 1 u 2 +11,2136 u 1 u 3 +7,159 u 1 u 4 +0,529 u 2 2-8,346 u 2 u 3 -
-
- 6,161 u 2 u 4 -8,607 u 3 2+6,29 u 3 u 4 +6,227 u 4 2;
y 2 ( u )=13,1-9,098 u 1 -2,232 u 2 +4,435 u 3 -2,235 u 4 -8,648 u 1 2+3,531 u 1 u 2 -
-
- 15,604 u 1 u 3 +5,491 u 1 u 4 +0,067 u 2 2+2,361 u 2 u 3 +
+0,502 u 2 u 4 -3,986 u 3 2--5,336 u 3 u 4 +0,5 u 4 2; (3)
y 3 ( u )=17+0,398 u 1 +0,964 u 2 +1,388 u 3 -0,437 u 4 +0,226 u 1 2-0,424 u 1 u 2 +
+5,264 u 1 u 3 -1,84 u 1 u 4 +0,507 u 2 2+0,091 u 2 u 3 -0,772 u 2 u 4 -
-
- 1,56 u 3 2-0,027 u 3 u 4 +0,702 u 4 2,
где u 1 - вариация (относительно х1 ) степени диссоциации аммиака 10-1 %;
u 2 - вариация (относительно х2 ) температуры процесса 10-1, оС;
u 3 - вариация (относительно х3 ) длительности процесса 10-1, час;
u 4 - вариация (относительно х4 ) напряжения на электродах 10-3, V.
Математическая модель (2) многофакторного процесса азотирования позволяет выявить наиболее критичные параметры и задать определяющие направления совершенствования используемых и разрабатываемых технологических установок получения азотированного слоя. Координаты оптимального режима, в котором показатель качества азотирования вида уi ( u ) ( i =1,2,3) может иметь внутренний максимум или минимум, дает следующая формула:
ui *=- Bi -1 A T ei /2, (4)
где Т – операция транспонирования (вектора, матрицы).
Комбинируя предыдущие результаты, аналитический расчет оптимального режима азотирования, обеспечивающий максимальную твердость, износостойкость и толщину азотированного слоя обрабатываемой поверхности, представляет следующий вид целевого функционала [4]:
F ( u )= r 1 у 1 ( u )+ r 2 у 3 ( u )+ r 3 у 3 ( u ), (5)
или при r 1 =0,5, r 2 =-0,3, r 3 =0,2 согласно модели (3):
F ( u )=48,17-29,729 u 1 -0,99 u 2 +3,632 u 3 +3,579 u 4 --29,517 u 1 2+11,526 u 1 u 2 +11,341 u 1 u 3 +1,564 u 1 u 4 +0,346 u 2 2- (6)
-
-4,863 u 2 u 3 -3,4 u 2 u 4 -3,42 u 3 2+4,74 u 3 u 4 +3,1 u 4 2.
Стационарная точка задачи оптимизации вида max F ( u ) для линейно-квадратичного функционала позволяет вычислять параметры оптимизации режима азотирования.
-
В векторно-матричном представлении данная точка (вектор-столбец) согласно модели (2) имеет координаты
u *=-( r 1 B 1 + r 2 B 2 + r 3 B 3 )-1(( e 1 + e 2 + e 3 )Tdiag[ r 1 , r 2 , r 3 ] A )T/2, (7)
или, то же самое, в физических размерностях с учетом «отсчета» от опорного режима х уравнение (7) определяет следующие эффективные технологические параметры режима азотирования:
u *T=[46,76 % 537,794 оС 19,378 час -21,3 V]. (8)
Полученный выше математический результат (в частности координаты стационарной точки режима азотирования) находится в хорошем соответствии с логикой физических рассуждений (рис. 1 - 6):
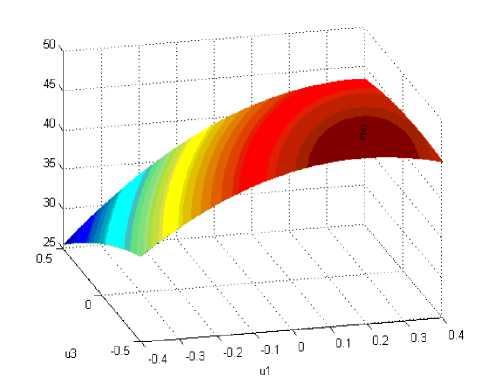
Рис. 1. Фрагмент целевого функционала F(u1, u3) в окрестности стационарной точки (4)
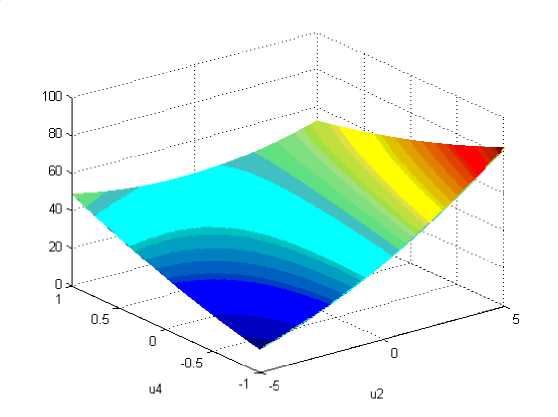
Рис. 2. Фрагмент целевого функционала F(u2, u4) в окрестности стационарной точки (4)
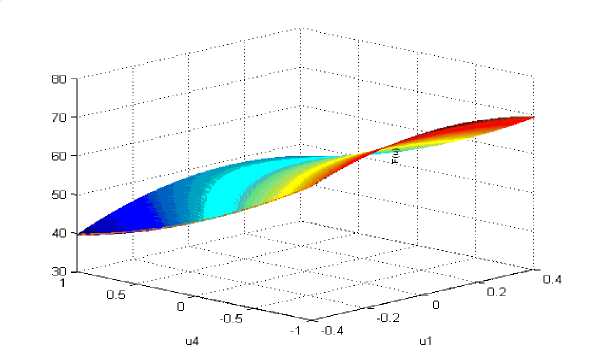
Рис. 3. Фрагмент целевого функционала F(u1, u4) в окрестности стационарной точки (4)
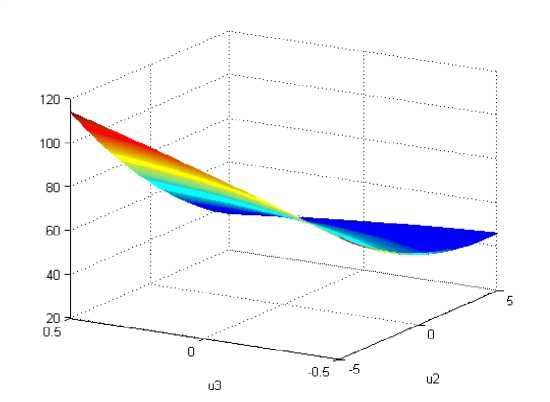
Рис. 4. Фрагмент целевого функционала F(u2, u3) в окрестности стационарной точки (4)
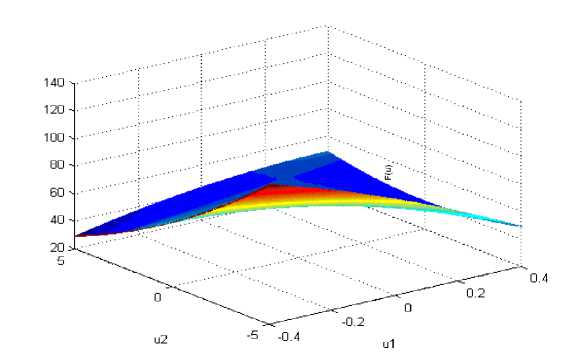
Рис. 5. Фрагмент целевого функционала F(u1,u2) в окрестности стационарной точки (4)
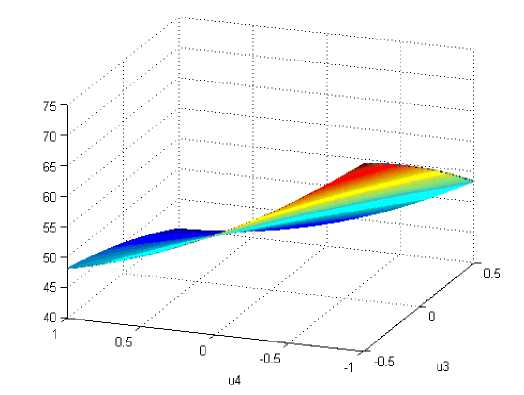
Рис. 6. Фрагмент целевого функционала F(u3,u4) в окрестности стационарной точки (4)
В стационарной точке u * функционал качества F ( u ) достигает своего «max» по переменным u 1 и u 3 и «min», соответственно по u 2 и u 4 , т.е. u * - седловая точка функционала (6). Физический смысл этого положения с учетом (8) означает следующее: нельзя для структуры (6) превышать степень диссоциации аммиака более чем на 46,76 %, для которой длительность азотирования равна 19,378 час. При этом одновременно не стоит опускать (делать меньше) температуру печи ниже 537,794 оС, а общий потенциал электростатического поля понижать ниже 21,3 V (см. рис. 1 - 6); в противном случае нарушение этих технологических параметров будет снижать эффективность процесса электростатического азотирования в смысле достижения осреднен-ного показателя качества (6).
Таким образом, обобщая оба этапа оптимизации процесса азотирования в электростатическом поле размерновосстановленных распределителей аксиально-поршневых насосов (гидромоторов), аналитически установлено, что при соответствующей обработке изучаемой группы изделий, изготовленных из конструкционной стали 38Х2МЮА, оптимальными параметрами процесса азотирования следует считать: степень диссоциации аммиака – 25 %; температура процесса – 550 °С; длительность процесса – 25 час (40 час по стандартной технологии для получения слоя 0,4мм [5]); знак потенциала на обрабатываемых деталях – «минус»; напряжение на электродах – 1800 V.


