Байесовский подход к наибыстрейшему обнаружению разладки в частично наблюдаемых марковских случайных процессах

Мы рассматриваем задачу обнаружения разладки, в которой в качестве модели эволюции процесса, во времени используется скрытая марковская модель (далее СММ). СММ

представляет собой частично наблюдаемый марковский процесс, состоящий из: 1) дискретного во времени скрытого от наблюдателя марковского случайного процесса, задающего пространство состояний системы S" = [Si,..., S" с начальным состоянием So, и из 2) дискретного во времени наблюдаемого случайного процесса УД = [Yi,..., У"], предоставляющего косвенную информацию о состоянии системы [1].

Математически СММ описывается следующим образом: задаются

• 1)    конечное (ф-мерное пространство состояний, из которого задается состояние {0,... ,d — 1}, начальное состояние So инициализируется с помощью следующей функции вероятности:

Р (So = so) = tt(s o );

• 2)    матрица вероятностей перехода (параметризованная 0) между состояниями из s_n-i в s„:

^{Р S} — ^sn^|Sn-1 — ^sn— 1) — ^рӨ (Sn-i, S"), ^п — 1, 2, . . . ,                     (1)

• 3)    условная функция плотности (параметризованная 0), характеризующая наблюдаемый процесс У в каждый момент времени п в зависимости от состояния системы:

У" - Jө (Y„|y„-i,s„), п = 1,2,...

Разладка — изменение вероятностного закона, описывающего СММ, происходит в неизвестный момент времени /. Матрица вероятностей перехода (1) и модель наблюдения (2) претерпевают изменение (из 0о в 01) в момент разладки /. В последовательной постановке, пока поведение наблюдений согласуется с нормальным состоянием, следует продолжать процесс. Если поведение наблюдений изменяется, то нужно как можно скорее обнаружить это изменение (разладку). На рис. 1 приведен пример наблюдения, удовлетворяющего СММ, а на рис. 2 — пример обнаружения разладки в нем.

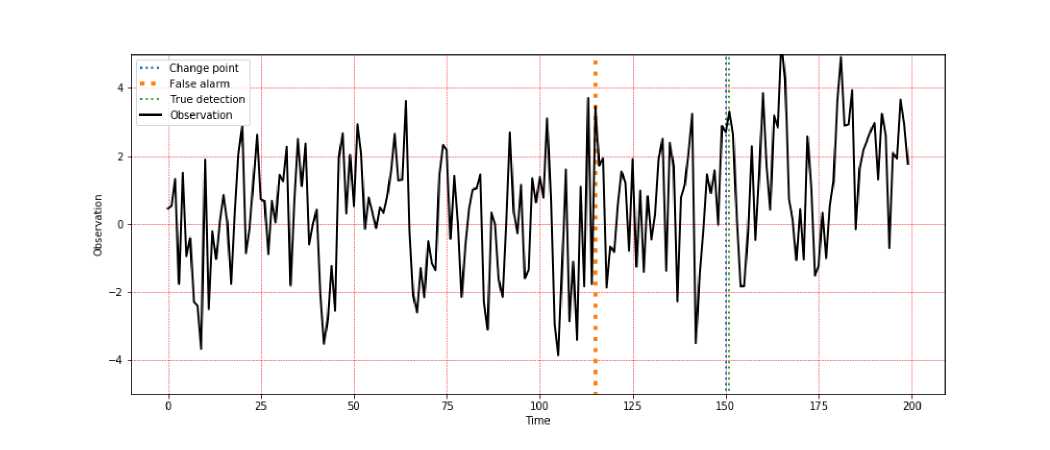
Рис. 1. Пример наблюдаемого процесса.

В данной работе мы рассматриваем байесовскую постановку задачи (раздел 2). Для неё мы изучаем и сравниваем рабочие характеристики трех наиболее популярных наибыстрейших правил обнаружения разладки (раздел 3): процедура. Ширяева, процедура. Ширяева-Робертса, процедура. Кумулятивных Сумм (КУСУМ). Процедура. Ширяева, оптимальна, в случае независимых и одинаково распределенных наблюдений в байесовской постановке, в которой момент изменения — случайная величина, из геометрического распределения [2]. Поскольку процедура Ширяева плохо применима на практике, интересно изучить, насколько хуже рабочие характеристики имеют процедуры Ширяева-Робертса, и КУСУМ, которые не используют априорное распределение момента разладки. Исследование проводится для двух моделей: СММ с Гауссовским наблюдением (раздел 4) и СММ, описывающая задачу прекращения сопровождения цели (раздел 5). В разделе б представлены выводы по проделанной работе.

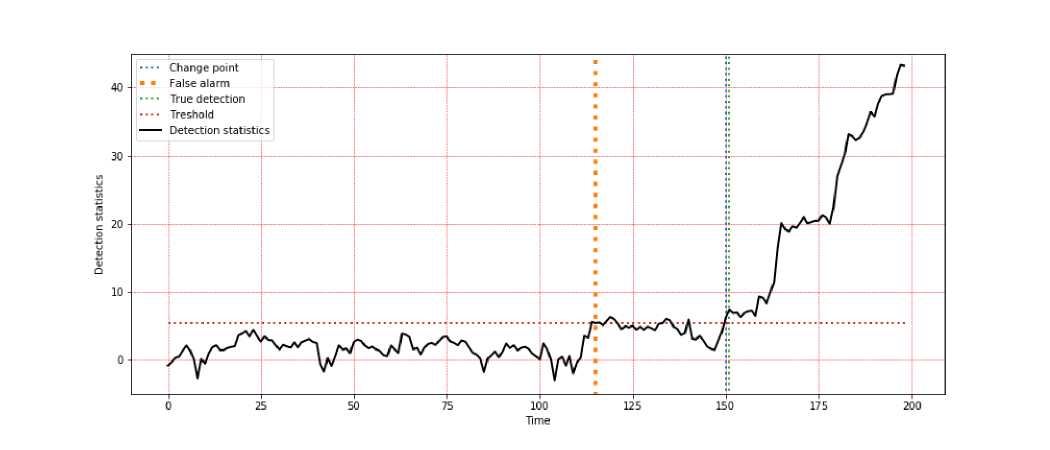
Рис. 2. Пример обнаружения разладки в наблюдаемом процессе

2.    Байесовская постановка

Рассмотрим байесовскую постановку, в которой момент разладки и — случайная величина, не зависящая от наблюдений. Мы считаем, что распределение вероятностей Р(и = к) = Тк, к = 0,1, 2,..., является геометрическим:

Р(и = к) = р(1 — р)^к,    к = 0,1, 2,...,

где 0 < р <  1.

Любая последовательная процедура обнаружения разладки — это правило, останавливающее наблюдаемый процесс {X_n}_nEz + ^в момент времени Т. Ложная тревога происходит, когда Т 6 и.

Обозначим Рк вероятность, когда разладка происходит в момент времени и = к Е Z + , Z = {0,1,...}, Ек — соответствующее математическое ожидание Р^-(•) = ЕГ=оГ^Рк(•), Е^- — математическое ожидание по мере Р^-.

Из [3] в байесовской постановке риск, связанный с ложным срабатыванием, обычно измеряется как взвешенная вероятность ложной тревоги (probability of false alarm — PEA):

∞

РҒА(Т ) = Р^- (Т 6 и) = £ г_кР^(Т 6 к).                  (4)

к =1

В свою очередь риск, связанный с задержкой в обнаружении, обычно измеряется как средняя задержка обнаружения (average detection delay — ADD):

∞

^г_к Ек[Т — к|Т > к]Р^(Т > к)

АПП(Т ) = Е^-[Т — и |Т >  и ]

к =0 _______________________________

1 — РҒА(Т )

Мы рассматриваем класс процедур обнаружения C_a = {Т : РҒА(Т ) 6 а}. Вероятность ложной тревоги ограничена а, 0 < а < 1. Цель байесовской постановки задачи — найти оптимальную процедуру, которая минимизирует в классе C_a среднюю задержку обнаружения.

• 3.    Процедуры обнаружения разладки

• 3.1.    Процедура Ширяева

Пусть «Нк : ? = к» и «Н^ : ? = то» — гипотезы, что разладка в наблюдении происходит в момент времени 0 6 к < то, и что разладка не происходит никогда, соответственно. Отношение правдоподобия между этими гипотезами:

_n= Р (ЭДН)

^к Р _:у- Н . , •

Из [4] статистика процедуры Ширяева, в которой используется параметр априорного распределения (3) момента разладки р, определяется как

V11     к- 1 -n ^Р ) -V^fi    А- - -п_Ппп

Rn,_P        ^{1 -р)}       р (_У„|н )           ^{- р) L} .                 (а)

к =і                    ^{v 11 х} к =і

Процедура Ширяева оптимальна в случае независимых и одинаково распределенных наблюдений в байесовской постановке с геометрическим распределением момента изменения в наблюдениях. Если отношение правдоподобия не зависит от момента разладки к, что всегда верно в случае независимых и одинаково распределенных наблюдений и часто для марковских и скрытых марковских моделей [4], т.е. (6) сводится к L_n = Р₀(УГ|У₁^п-1)/Рго(УГ|У₁^п-1), статистика R_n,_p удовлетворяет рекурсии

ℒ

^Rn,p = (1 + ^Rn- 1 ,p ⁾"₁ -----■ ^л > 1, ^R o ,p = 0.                         (8)

^{1 —} Р

Процедура Ширяева относительно порога А определяется как

Т_А = inf {л > 1 : R_n,p > А} , А > 0.                         (9)

• 3.2.    Процедура Ширяева-Робертса

Из [4] статистика процедуры Ширяева-Робертса R_n определяется как

п

Р V Нк

Р ( А^п' Н . ,.

(Ю)

R. = С к=

Если £_п не зависит от момента разладки к, тогда из [4] статистика процедуры Ширяева-Робертса удовлетворяет рекурсии

Rn = (1 + Rn-i )£п, л > 1, Ro = 0.

(И)

Процедура Ширяева-Робертса относительно порога В определяется как

Т_в = inf {л > 1 : R_n > В} , В > 0.

• 3.3.    Процедура КУСУМ

4.    СММ с Гауссовским наблюдением

Из [4] статистика КУСУМ Vn = eWn в экспоненциальной форме определяется как С -max 11 max 1 АД1НЕ 11                  ,

V„ =max^, max, y(y„|H^)j )■ и если Ln не зависит от момента разладки к, то из [4] статистика КУСУМ удовлетворяет рекурсии

Vn = max {1,Рп-1 }L_ni л >  1, Vo = 1.                     (14)

Процедура КУСУМ относительно порога С определяется как

Т_с = inf {л > 1 : Vn >С } , С >  0.

Мы рассматриваем задачу, в которой текущий наблюдаемый сигнал и последующее состояние зависят от текущего состояния (пусть (d = 2)-мерное пространство состояний). Тогда матрицы перехода (1) из предыдущего состояния в текущее Рө₀ (S_n = s_n|S_n-1 = s_n-1) и рд 1 (S_n = s_n|S_n-1 = s_n-1) — до и после разладки соответственно

, х    /1 - а_ө 0     а_ө 0 \           , х    /1 - а_ө 1      а_ө 1 \

^{Р Ө}0 V   Зө ,     1 - Зө ,) ’     ^РӨ1 (•’•⁾    V   Зө і     1 - Зө і) '

Если ? — момент разладки, модель наблюдений (2) /ө₀(Y^-1 ls^-1) и /ө1 (Yls^) — модель наблюдений до разладки и после разладки соответственно.

Используя правило Байеса и то, что Р (Y1| Y^i-1, H^) = Р (Y11 Y^i-1, Н») для 1 < I <  к — 1, получаем из (6) отношение правдоподобия (£П)^:

п

^=п i=1

Р (Y1 |YI^-1, Щ) Р (Г |YI^-1, Н»)

^п Р (Y1|Y1^1-1, Н) i=1 Р (Y1|Y1^1-1, н » ) ■

Пусть г¹» = Р(Si = г|Г/ 1, Н»), г = 0,1. Непосредственное вычисление для Р (Yi|Yi^-1, Н » дает

Р(Yi|Y11-1, Н») =    » fөo(YilSi = 0) + г^/ө,(YilSi = 1), I = 1,2,...(17)

Тогда ri » удовлетворяет следующей рекурсии:

,   = Рө, (O,i)r0_1.»/<0 (Yf-1|Sf-1 =0)+ Рө, (СОЩ,»./», (Yi-1 |Si-1 = 1)

r‘"            г0-1,„/өо (Yi-1|Se-1 = 0) + г1-1,„/ө0 (Y,-1|S,-1 = 1)         ,(1S> r0,» = Р (S0 = г)=^ө,(г),   г = 0, 1.

^ПУ^{СТЬ r}i,i = ^{Р (S}i = ^^|Y1ⁱ 1, ^Н1), тогда, обобщая (17) для Н^, получаем выражение для Р (Y1IY/^-1, Н):

Р(Yi|Y1i-1, Н1) = г0°1 fөa(YilSi = 0) + rXkfөa(YilSi = 1), I > к.(19)

Рекурсия для ri _к имеет вид

Рө_а^(0,г)^ге- 1 ,к fө_b ^{( y} i - 1 ^{| s} i - 1 = ^{0) +} Рө_а ⁽M^)rL1,_fc /ө_ь ^{( y} i - 1 ^{| s} i - 1 = 1)

30-11 fөb (Yi-1lSi-1 = 0) + r1-1i fөb (Yi-1lSi-1 = 1)         ,(20)

^r0,i = ^{Р (S}0 = ^г)=^ө,^(г),    г = ^0,1

где

{ 0, если I <  к

1, если I > к ’

6={

0,

1,

если I < к если I > к

Вычисляя из рекурсий (18) и (20) ri» и ri _к, мы получаем Р (YilY ^ 1, Н») и Р (Yi|Y1^i-1, Н1) из (17) и (19) соответственно. Затем, подставляя полученные значения в (16), получаем отношение правдоподобия £_к, которое используется при вычислении статистик для процедур обнаружения разладки Ширяева, Ширяева-Робертса, КУСУМ (7),

(Ю), (13).

4.1.    Численное сравнение алгоритмов обнаружения разладки

Для вычисления рабочих характеристик рассматриваемых процедур обнаружения используем метод Монте-Карло. Для каждого прогона Монте-Карло моделируем СММ: последовательность состояний {Sn^j)}, п > 1 (j = 1,..., N, N — число прогонов Монте-Карло), используя модель Бернулли, и соответствующую ей последовательность наблюдений {У^')}. Также мы генерируем случайный момент разладки v j согласно геометрическому распределению (3). В каждом прогоне Монте-Карло мы получаем, согласно (9), (12), (15), время остановки Т _А\ тВ\ Т ( ' ) , j = 1,...,N для процедур Ширяева, Ширяева-Робертса и КУСУМ соответственно. Прогоны Монте-Карло, которые приводят к ложным срабатываниям, т.е. Т ^(j)<  Vj, используются для вычисления экспериментальных оценок Монте-Карло вероятности ложной тревоги PFA (4):

1 N ^Ғ1

• ( а) = N У},

j=i

• 1    N

  - АТв) = N У H(ro><„jl,(21)

j=1

• 1    N

  - ¹

• ( c) = N У}.

j=i

Тогда экспериментальная оценка Монте-Карло средней задержки обнаружения ADD (5)

1 N1

А\(Та ) = — У (т ( ' - V. ) 1Шук _г---

^А N j=y ^{а j}) №>„_б ^} 1 - _рға ( т _а )

АПП ( Т_в ) = — У ^Т(j) - V,-)               ----

^В N j=A ^{в j}V ^{т^ ^} 1 - р_ҒА(Т_в )

1 N                                    1

АБЬ(Т_С ) = — У (т - v,-)              ---

N j-Л ^{c j}V № >^з ^} 1 - р_ҒА(Тс )

Параметры моделирования

• 1)    Параметры СММ: а_е0 = 0.2, а_е 1 = 0.35, ^е₀ = 0.5, р_Ө1 = 0.4,

( V(1,1)    если S

До разладки : Y_n = <

V (-2,1) если S,

После разладки

JV(2.5,1)    если Sn = 0

V(-0.5,1)   если S_n = 1.

Эта разница тем меньше, чем меньше р. Наиболее популярная на практике процедура КУСУМ имеет хуже характеристики, чем процедуры Ширяева и Ширяева-Робертса. Этот проигрыш уменьшается с уменьшением р, но все равно остается заметным.

Таблица!

Рабочие характеристики алгоритмов обнаружения

р	a	adXt a )	ADD(TB )	ADD(TC )	PFA ( T a )	PFA(TB )	PFA ( T c )
0.5	0.2	0.64	0.67	0.81	0.177	0.178	0.184
0.5	0.15	0.80	0.89	1.12	0.139	0.131	0.133
0.5	0.1	1.09	1.12	1.50	0.095	0.087	0.094
0.5	0.05	1.28	1.34	1.71	0.074	0.072	0.075
0.5	0.01	2.98	3.23	4.05	0.009	0.009	0.0087
0.1	0.2	2.83	2.91	3.04	0.183	0.190	0.207
0.1	0.15	3.28	3.35	3.50	0.139	0.143	0.151
0.1	0.1	3.77	3.90	4.07	0.094	0.92	0.103
0.1	0.075	4.35	4.41	4.58	0.074	0.071	0.75
0.1	0.01	7.80	7.89	8.09	0.0095	0.0105	0.0098
0.01	0.2	7.21	7.71	8.02	0.201	0.188	0.204
0.01	0.15	7.76	8.28	8.54	0.148	0.118	0.120
0.01	0.1	8.52	8.81	8.96	0.094	0.099	0.097
0.01	0.075	9.36	9.66	9.85	0.074	0.062	0.080
0.01	0.01	13.54	13.77	13.98	0.0095	0.0088	0.0101

5.    Задача прекращения сопровождения цели

Для иллюстрации практической применимости СММ рассмотрим задачу прекращения сопровождения цели в активных сонарных системах [6]. Из-за постоянно меняющихся подводных условий, в частности, геометрических, географических эффектов, реверберации, отношение сигнал-шум (SNR) может существенно изменяться. Из-за этого производительность датчика при каждом последовательном сканировании может резко меняться: между низким и высоким уровнем обнаружения на каждом сканировании. Чтобы решить эту проблему, разумно использовать СММ. Марковская цепочка (скрытая от наблюдателя компонента) состоит из двух возможных состояний, соответствующих высокой и низкой вероятности обнаружения. Наблюдаемая компонента — последовательность сканов, на каждом из которых цель присутствует или нет. Вероятность обнаружения цели на каждом последовательном скане зависит от состояния обнаружения (скрытой компоненты). Таким образом, задача прекращения сопровождения цели в активных сонарных системах может быть рассмотрена как задача наибыстрейшего обнаружения разладки с СММ: если разладка не произошла (цель присутствует в наблюдаемой зоне), следует продолжать наблюдение и сопровождение цели, но, если разладка произошла (цели в наблюдаемой зоне больше нет), необходимо это обнаружить как можно скорее и прекратить наблюдение и сопровождение.

Обозначим {X_n} скрытую марковскую компоненту. Тогда X_n = 1 соответствует состоянию с высокой вероятностью обнаружения сонаром (SNR большое), и X_n = 2 соответствует состоянию с низкой вероятностью обнаружения сонаром (SNR низкое). Таким образом, X_n Е {1, 2} — скрытая Маркове кая цепочка. Пусть Pj — вероятность перехода между состояниями, где j = той j = 0 задают вероятность перехода до и после разладки соответственно. Тогда Pj(X_n = 1|X_n-i = 2) = pj (2,1) = р, n >  1 — вероятность перехода из состояния с низким SNR в состояния с большим SNR, и Pj(X_n = 2|X_n-i = 1) = pj (1, 2) = q, n >  1 — вероятность перехода из состояния с большим SNR в состояния с низким SNR. Начальное состояние Xo определяется из распределения Pj (Xo = 1) = 7Tj (1) = р/(р + q) для j = той j = 0.

Согласно гипотезе до разладки H^ : v = то, условная плотиость наблюдений Y р(Үп|ҮП-1,Хп = I, H^) = ді(Үп), I = 1, 2, n > 1, и согласно гипотезе Hk : v = к, наблюдения после разладки Yk, Yk+1,••• являются независимыми и одинаково распределенными с плотностью /(у).

Таким образом, совместная плотность до разладки вектора ҮП:

п

P V    П Р~(ЭД-1).(23)

i =1

Совместная плотность вектора ҮП, при условии, что v = к < n:

к-1п

Рк (Y^ = П Р-(Үг|Үг-1) х П (Үк).( i=1

Таким образом, используя (23) и (24), преобразуем отношение правдоподобия (6):

7 = / ү _;_ ү ү П^-1).

Так как отношение правдоподобия в данном случае не зависит от момента разладки v, то для подсчета статистик процедур обнаружения мы будем использовать формулы (8), (И), (14).

В (23) p^(y|YJ-1) есть не что иное, как

■.№іү г^-1)= е 9i(Yi)p (х = i i y г^-1), г > 1,

1=1

где Р(Хг = 1|үі 1) = Рг|г—1(1) — апостериорная вероятность, и она может быть посчитана как

Pi|i-1(2) = Рг-1(2)(1 - р) + Pi- 1 (1)q, Рг_М(1) = Рг-1(1)(1 - q) + Рг-1(2)р,    (27)

где Р_г(1) := Р (Хг = l| Yi) — апостериорная вероятность, которая, согласно формуле Байеса, получается

_Р =      ді(Үі)Рі|і-1(1)

ⁱ⁽ )  Е2=1 дв^Рц-М .

Как описано выше, наблюдение {Үг} — последовательность обнаружений цели на каждом скане. Если цель обнаружена на n-м скане, то Үп = 1, но если цель не обнаружена на n-м скане, то Yn = 0. При моделировании мы используем схему Бернулли, в которой успех (Үп = 1) задается вероятностями обнаружения при однократном сканировании РД и РД для большого и низкого SNR соответственно. Тогда ді(Үп) = (Р^ү" (1   Р'    -', I = 1, 2; /(Үп) = (Р/а)у- (1 - Pfa)1-Y",        (29)

где Р 1 Рд, и Р^а удовлетворяют неравенствам РД > РД > Р$_а.

Используя формулы (26), (27), (28), (29), получаем отношение правдоподобия (25), которое используется при вычислении статистик для процедур обнаружения разладки Ширяева, Ширяева-Робертса, КУСУМ (8), (И), (14).

5.1.    Численное сравнение алгоритмов обнаружения разладки

Моделируем стохастическую модель: ({Х_п}, {Іф}щ/), используя генератор случайных чисел. Для каждого прогона Монте-Карло получаем, согласно (9), (12), (15), время остановки Т/. тВ\ Т^), z = 1,... ,N. Вычисляем ADD и PFA аналогично (22) и (21).

Параметры моделирования

• 1)    Параметры СММ: р = 1/30, q = 1/10, Pi = 0.9, Pi = 0.1, P_fa = 0.1.

• 2)    Параметр геометрического распределения: р = 0.5; 0.1; 0.01.

• 3)    Заданный уровень, ограничивающий PFA: a = 10^-1; 10^-2; 10—³; 10^-4.

• 4)    Порог для процедуры Ширяева выбирается как А = (1 — a)/a, а для процедур Ширяева-Робертса л КУСУМ - В = (1 — р)/(ра).

6.    Заключение

Результаты моделирования.

Результаты моделирования представлены в табл. 2. Как и для модели из раздела 4, процедура Ширяева-Робертса лишь незначительно уступает процедуре Ширяева, при р ^ 0 разница становится совсем незаметной. В свою очередь популярная процедура КУСУМ для данной модели имеет весьма низкие рабочие характеристики, заметно уступая и процедуре Ширяева, и процедуре Ширяева-Робертса.

Т а б л и ц а 2

Рабочие характеристики алгоритмов обнаружения

Pfa = 0.1,р = 1/30,q = 1/10, Pi =0.9, Pi = 0.1
р	a	ADD ( T a )	AdD(T b )	AdD(t c )	PfA ( T a )	PfA ( t b )	PfA ( t c )
0.5	0.1	1.533	1.764	4.745	0.09145	0.08647	0.09155
0.5	0.01	4.320	5.137	31.164	0.00981	0.00983	0.00997
0.5	0.001	7.647	8.8643	49.070	0.000906	0.000904	0.00092
0.5	0.0001	10.721	11.955	54.379	0.000098	0.000092	0.000093
0.1	0.1	12.177	12.237	40.339	0.09325	0.09276	0.09025
0.1	0.01	28.486	28.818	55.942	0.009334	0.009106	0.009366
0.1	0.001	45.466	46.187	75.039	0.000962	0.000932	0.000903
0.1	0.0001	63.546	63.617	94.514	0.000092	0.000092	0.000086
0.01	0.1	70.381	70.519	77.805	0.09795	0.097176	0.09858
0.01	0.01	134.448	134.672	141.706	0.009812	0.00999	0.00994
0.01	0.001	199.416	200.332	206.377	0.00097	0.00096	0.00099
0.01	0.0001	264.739	266.71	269.840	0.000098	0.000097	0.000090
0.001	0.1	166.184	166.280	170.473	0.09861	0.0979	0.09992
0.001	0.01	256.426	258.430	260.535	0.009866	0.00956	0.009801
0.001	0.001	344.781	344.810	349.665	0.0009866	0.00094	0.00090
0.001	0.0001	432.422	432.572	436.921	0.000098	0.000098	0.000096

Было проведено исследование рабочих характеристик наиболее популярных наибыстрейших процедур обнаружения разладки Ширяева, Ширяева-Робертса, КУСУМ. Критерием эффективности для их сравнения служила средняя задержка обнаружения ADD при ограниченной вероятности ложной тревоги PFA. В качестве модели наблюдения использовались две различные скрытые марковские модели. В результате моделирования получено, что для обеих моделей процедура Ширяева имеет наилучшие рабочие характеристики. Однако процедура Ширяева-Робертса, не использующая, в отличие от процедуры Ширяева, априорное распределение момента разладки, имеет рабочие характеристики лишь незначительно хуже, чем процедура Ширяева. Эта разница уменьшается при р ^ 0. В свою очередь наиболее популярная процедура КУСУМ уступает обеим процедурам (в первой модели незначительно, но во второй существенно). Исходя из полученных результатов, мы рекомендуем использовать процедуру Ширяева-Робертса в практических задачах по обнаружению разладки в скрытых марковских моделях. Результаты исследования очень полезны и для большинства других приложений.

Работа была поддержана грантом Россиского Научного Фонда 18-19-00452 в МФТИ.