Baker Map's Itinerary Based Image Scrambling Method and Its Watermarking Application in DWT Domain

With the fascinating developments of multimedia and network technology during the past decade, the digital contents of images, texts, audio or video, have been widely communicated over the Internet and wireless networks. These digital products bring us lots of convenience and pleasure. However, they can be replicated, edited easily and spread openly through the Internet, which causes a serious problem that it is difficult even impossible to give proof of copyright once pirated. As a result, the copyright isn’t protected legally, and the authors of digital multimedia may feel economically deprived of their reputations by fake copies. To meet the demand of copyright and intelligent property protection, various watermarking algorithms have been proposed and developed, see for example [1-7]. A watermarking technique is to prevent digital images that belong to rightful owners from being illegally commercialized or used. The basic principle of watermarking is to modify the host data in a perceptually invisible manner by embedding a weak signal in the host data without altering it significantly. By detecting the modifications to verify the existence of the watermark in order to prove an author’s ownership of some original data, or trace the illegal use of the data, the author’s identity and ownership rights are protected. In contrast to encrypted data, watermarked data can still be used while remaining protected. It does not necessarily prevent the copying of digital data, but should rather identify the original data source, so that copyright violations can at least be detected. The hidden signal travels with the data, which thus remains “marked” and protected, till the intended receiver removes the watermark. Since a watermark is used to prove ownership, there are several important issues in the watermarking system including transparency, robustness, and blindness. As for a watermarking algorithm, its robustness is essential. The watermark must be able to effectively resist common image attacks, such as filtering, nosing, cropping or JPEG compression. Transparency is also required so that a watermark may remain invisible in order to maintain its secrecy. Transparency is also needed to prevent the visual distortion of an original image to maintain the commercial value of the image. A watermarking technique is referred to as blind if the original image and watermark are not needed during extraction [7-9]. The blindness is necessary if it is difficult for us to obtain the original image and watermark.

There are two methods of performing watermarking, one in spatial domain, and the other in frequency domain. Each technique has its own advantage and disadvantage. Watermarking in the spatial domain is easy to implement by embedding a watermark in selected areas on the texture of the host image by changing the gray levels of some pixels [10,11]. The disadvantage of this kind of watermarking is that the inserted information may be easily detected using computer analysis and the watermark cannot effectively resist image processing attacks such as compression, noise, and filtering. In recent years, the spectral domain has been widely used for watermarking, since the spread spectrum communication is robust against many types of interference and jamming. The host image is transformed to the frequency domain by Discrete Cosine Transform (DCT) or DWT etc. The watermark bits are then embedded in the mid-frequency of the transformed host image to ensure the simultaneous transparency and robustness of the watermarked image [12,13].

In order to enhance the robustness against attacks, a variety of improved watermarking schemes have been proposed recently, see for example, [14-19]. As for the watermarking in the spatial domain, the common way is to perform preprocessing to the host image and/or the watermark by some scrambling algorithms, which makes the watermarks more transparent and strongly robust [2022]. As an approach of image encryption, digital image scrambling technology is a research emphasis all through. It can be used directly in digital encryption, and can also be used as the preprocessing and post processing to enhance the robustness of digital image hiding and digital image watermarking. The basic idea of the technology is to change the image pixel positions through matrix transform to achieve the visual effect of disorder. The idea can also be expanded to the color space and frequency domain. There are several methods for image scrambling such as Arnold cat map, Baker map, Standard map, etc. [23-26]. The scrambling algorithms have two advantages. On one hand, it makes the watermark bits spread uniformly all over the host image. Therefore, it can resist the attacks such as cropping, noise, compression, filtering effectively. On the other hand, it can also enhance the security for the watermarking scheme by setting the encryption keys. Only the authorized owners know the secret keys to restore the watermark and the original host image. Many researchers have been focusing on security. The common way is design some secure scrambling schemes to manipulate the preprocessing in watermarking. Thanks to the good properties of watermarking in the spectral domains, the scrambling of the transformed coefficients for both the watermark and the host image shall be a good preprocessing approach. The hybrid image watermarking schemes in the spectral domain combining the scrambling preprocessing are expected to be more robust to resist many types of attacks.

As we know, there are two problems must be solved in watermarking. One problem is how to extract the watermark by using blindness schemes. The other problem is that although a watermark embedded in the significant coefficients can obtain robustness, but the watermarked image is easily visible distortion. In a watermarking system, the quality of a watermarked image is more important than the robustness of watermarking. Visually, even if there exists only a little distortion in the watermarked image, the watermark will easily be detected and destroyed. Hence, in this paper, we propose a wavelet-based blind watermarking algorithm combining with the scrambling scheme based on the itineraries of the improved 3D Baker map. Both the coefficients in LH2 and HL2 sub-bands are used to embed the watermark bits. Assume that the host image is one with gray-scale level 256 sized 512 by 512 and the watermark is one binary image W sized 64 by 64. The scrambled watermark W ' is rearranged to be a vector W '' of size 1 × 4096 , and W '' is divided into two vectors W = W ''(0:2047) and W = W ''(2048:4095) . They are respectively embedded in medium frequency sub-bands LH2 and HL2, which are of the same size 128

by 128. To embed the watermark bits, both LH2 and HL2 are divided into non-overlapping blocks of size 2 by 2, so as to consider them as the matrices with 64 × 64 blocks. Then the blocks in this two sub-bands are also scrambled several rounds respectively with the proposed scrambling scheme, and two new matrices LH2’ and HL2’ with 64 × 64 blocks sized 2 by 2 are derived. The watermark bits in W are embedded in the left part of sub-band LH2’ with 64 × 32 blocks. The order to embed is from top to bottom and then from left to right. In addition, the watermark bits in W are embedded in the right part of sub-band HL2’ in the same order. The embedding scheme is based on the odd-even adjustment rule and the neighbor mean value [27]. Experimental results show that the proposed method is very efficient in resisting various attacks and the watermarked image looks visually lossless.

The rest of the paper is organized as follows. The itinerary of the improved 3D Baker map used to encode the image pixel positions is introduced in Section II. Then the itineraries are employed for image scrambling in Section III. One watermarking scheme is proposed in Section IV. Section V concludes the paper.

• II.    Itinerary of 3D Baker Map

In this section, we shall give some definitions regarding itinerary for a chaotic map. We consider the 3D Baker map as an example.

Definition 1. If F is a map from X to X , and

• (i)    If x ∈Λ⊂ X , then F ( x ) ∈Λ ;

• (ii)    For any point b ∈Λ , there must be a point a ∈Λ , so that F ( a ) = b .

then the subset Λ is called an invariant set of F , that is F ( Λ ) = Λ .

Let the invariant set of F to be Λ= H ₀ H ₁и ... H , it’s not difficult to get a point x ∈Λ such that F^k ( x ) ∈ H , ( t = 0,1,..., N ), for all k ∈ Z .

Definition 2. Let F be a map with an invariant set Λ=H0H1и ... H , and int(H) int(H) =φ, for any i≠ j, i, j =0,1,...,N . Then any point x ∈Λ has a bilateral infinite string of symbols s = ⋅⋅ ⋅s s ⋅s ss ⋅ ⋅ ⋅ satisfying s =t, if Fk(x)∈H , t=0,1,...,N,k∈Z. (1) The string s is called the itinerary of x ∈Λ.

In fact, using the infinite string of symbols (itinerary) to determine a number is much similar to an integer in k -nary expansion. If F is the double map, the symbol string s = s s s ⋅ ⋅ ⋅ s truncated from an itinerary corresponds to the binary form of a positive integer. The correspondence is one-to-one [28]. In this paper, we use the truncated symbol strings 5 = 505|52'" ^v to encode the image pixel positions.

The 3D Baker map is constructed in [26] by

	„   -   2.. n        1 „        1 (2 x ,2 y ,-), 0 <  x < -,0 <  y <-
B ( x , y , z ) = •	(2 x ,2 y - 1, - + 1), 0 <  x <  1,1 <  y <  1 ,        ,4   2,             2,2 (2 x - 1,2 y , - + 1), 1 <  x <  1,0 <  y < 1 ,    ,4   4,  2          ,           2 z 3     1           1 (2 x - 1,2 y - 1,- + 3), - <  x < 1,- < y <  1 ,,,  ,
The process of this map is shown in Fig.1.

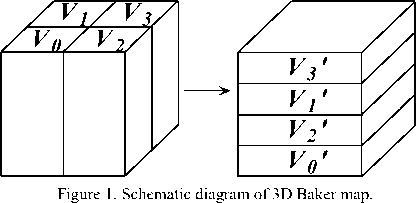
The unit cube V = [0,1] x [0,1] x [0,1] is divided into four small cuboids V , V , V and V , which are stretched in both x -axis and y -axis directions, and are compressed in z -axis direction. The 3D Baker map has intensive chaotic nature with invariant set V . We that the map (2) becomes the following map (3) as projected on xy plane.

D i ( x , У ) = D ⁽ x ) • D ⁽ У ) =•

(2 x ,2 y ), 0 <  x < ^- ,0 <  y < ¹

⁽² x ,2 y ^{- 1)} , 0 <  x < ^1,1 <  y < ¹

⁽ 2 x - 1,2 y), ^- <  x < ^1,0 <  y < ¹

(2 x - 1,2 y - 1), - <  x <  1,- <  y <  1

note V is

where D ( x ) is the so called double map defined

2 x , 0 <  x < — , ,                ₂,

D ( x ) = ‘

According to the definition of itinerary, if any point in V is marked by t ( t = 0,1,2,3 ), the unilateral truncated symbol string 5 = s₀s_xs₂ ••• 5_V of the point’s itinerary would be a quaternary integer. The itineraries of any two points ( x ₀, y ₀, z₀ ),( x ₀, y ₀, z _t) е V are the same under (2), so one can use the map (3) to get any point’s itinerary under the mapping of (2). The map (3) is also expansive, piecewise and continuous in both x -axis and y -axis directions. If any point in the square region I is marked by t ( t = 0,1,2,3 ), and the initial points distributing uniformly in the region I are corresponding to the pixel positions in a two-dimensional image, then we can get the quaternary code intercepted from the itinerary of the initial point for each pixel. Different pixel will have different code, which is suitable for image scrambling in the space domain.

As the codes derived from the double map are simple, the 3D Baker map (3) is improved to be the following form:

z11

⁽2 x ,2 y ,—), 0 < x < -^,0 < y <-

B '( x , y , - ) = ‘

Z 1.

(2 x ,2 - 2 y , - + -), 0 <  x < -,- < y <  1

,        ,4   2, z   1.    11

(2 x-1,2 y,- + -), -< x < 1,0 < y <4  4   22

z3    11

(2 x -1,2 - 2 y,- + -), — < x < 1, — <

,        ,4   4,  2,

The improved map (4) stretches the cuboids regions in x -axis and y -axis directions with the help of both double map and tent map. The itinerary of any point in the cubic region V can also be obtained from the map (5) which is the projection of (4) on xy plane. The map (5) is the product of the double map and the tent map.

(2 x ,2 y ), 0 <  x <  1,0 <  y < ¹

as

F ( x , y ) = D ( x ) • T ( y ) = ‘

(2 x ,2 - 2 y ),

(2 x - 1,2 y ),

0 <  x <-,-< y <  1

2,2

¹ <  x <  1,0 <  y < ¹

2,         2

⁽2 ^{x -} 1,^{2 - 2} y ), ¹ <  ^x <  I,¹ <  y <  1

Obviously, the map (3) is the product of two double maps.

2 x - 1, — <  x <  1. 2

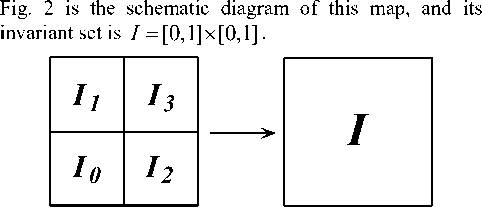
Figure 2. Schematic diagram of product of two double maps.

where T ( y ) is the so-called tent map with the form

(a) original image

2 У , 0 <  У < 1,

T ( У ) н

2 - 2 У , 1 <  У < 1.

• III.    Image Scramble Based on the Itinerary of 3D Improved Baker Map

Here we take a 2D gray image with size 2 N x 2 N for an example and introduce the process of encoding. Two initial matrices X and Y of size 2 N x 2 N are needed to record the code of each pixel. The elements in X and Y ^are initialized to X ( i , j ) = 2 ± 1, Y ( i , j ) = j ¹, for i , j = 0,1,2,...,2 N - 1 . It means that ( ² i ⁺¹,² j ⁺ 1) ^{,         , , ,   ,}                                             n + 1 , n + + 1

b) scrambled by one time

will be employed for iteration of the map (5) instead of the pixel position ( i , j ) . l et

• 1 0    = {( x , У )|0 ^ x <  1,0 <  y <  1},

• 1 1    = {( x , У )|0 <  x <  ¹,¹ <  У <  1},

• I 2    = ^{{( x} , У ^ <  ^x <  I,⁰ <  У < ^1},

I 3 = ^{{( x} , У ^)|1 < ^x < ^1,1 < У <  ^1} .

(c) scrambled by 4 times

The elements X(i, j) and Y(i, j) are iterated with (5) to obtain the itinerary for the pixel position (i, j) , the process is shown below.

• (i)    Let k = 0 .

• (ii)    Obtain the point ( x ( i , j ), у ( , , j )) = Fk (

  2 i + 1 2 j + 1

  N n + 1 , 2 N + 1 )

  
  

by (5).

• (iii)    If ( X ( i , j ), Y ( i , j )) g I t , t = 0,1,2,3 , then let

5 (i, j, k) = t, k = k +1.

• (iv)    Repeat steps (ii)-(iii) till k = N + 1 .

• (v)    Let S ( i , j ) = s 0 5 1 ... 5 N , where s_k = 5 ( i , j , k ) , k = 0,1,..., N . Then translate S ( i , j ) into decimal number.

  

  (d) scrambled by 10 times

  Figure 3. Results of scrambling.

  
  

A coding matrix S sized 2 ^N x 2 ^N can be obtained from the above process, and then we arrange the elements of S into a vector S ₁ of size 1 x 2 2 ^N in accordance with the order from top to bottom and from left to right. When a 2D digital image M with size 2 ^N x 2 ^N is being scrambled, it is necessary to arrange it into a vector M of size 1 x 2^{2 N} , and encoding each element with one nonnegative integer 0,1,2,...,2^{2 N} — 1 . In this simulation, we also take the order from top to bottom and from left to right to rearrange the elements in the matrix M . Then we can use the vector S to scramble the image.

Let M ( k ) = M ( ^ ( k )) , for k = 0,1,2,...,2 2 N - 1 , then rearrange M₂ into a matrix sized 2 N x 2 N in accordance with the same order. The scrambled image is at last obtained. The process to decode the scrambled image is similar to the above process, except one difference, that is, let M ( ^ ( k )) = M ( k ) , for k = 0,1,2,...,2² N — 1 . In this simulation, we use a 256

gray-scale image LENA sized 256 x 256 . The results of scrambling are shown in Fig.3. Fig. 3 (d) is used to test the robustness of this algorithm. Since the algorithm makes a more uniform distribution of the image pixels, the scrambled image has a stronger robustness to resist cropping attack. The images shown in Fig. 4 are restored from Fig. 3 (d) attacked by 1/4 area cropping of center, upper-left corner and lower right-hand corner, as well as

1/2 area bottom cro

ing respectively.

Figure 4. Restored images of the scrambled image attacked by cropping.

(a) 1/4 area cropping of center

(b) 1/4 area cropping of up-left corner

(a) salt and pepper noising with Density=0.2

(c) 1/4 area cropping of low-right corner

(b) Gaussian noising with Variance=0.1

(c) JPEG compression with Quality factor 50

energy of the original image and contains the important information about the image. Hence, if the watermark is embedded in the low-frequency sub-band, it will bring stronger robustness, but easily lead to image distortion. Meanwhile the capacity of this sub-band is limited. The coefficients in high-frequency band HH1 and HH2 reflect the details of the original image. Therefore, if the watermark is embedded in these sub-bands, it will bring lower visibility, but the robustness is weak as the watermark bits will be easily eliminated by a lossy compression and easily removed after low pass filtering. In this paper, we choose the mid-frequency sub-bands LH2 and HL2 to embed the watermark bits.

(d) JPEG compression with Quality factor 30

Figure 5. The reconstructed images of the scrambled image with attacks.

(a) Host image(LENA)

(b) Watermark (STU)

(c) Scrambled watermark

IV. Application to Watermarking

In this section, the scrambling algorithm proposed in Section III is used to shuffle the watermark and the blocks of DWT coefficients of the host image, so that the security and robustness of the watermarking can be strengthened. The host image is a grayscale image LENA with size 512 by 512 (see Fig. 6 (a)), and the watermark is a binary image of size 64 by 64 called STU (see Fig. 6 (b)). Before embedding the STU into the host image LENA, STU is scrambled 250 times with the scrambling algorithm proposed in Section III. On one hand, the watermark bits can be distributed more uniform in the host image, so as to reduce the distortion of the extracted watermark if the watermarked image is attacked. On the other hand, as scrambling times can be used as a key to increase the difficulty to extract the watermark, the information is securer. The scrambled watermark is shown in Fig. 6 (c).

The host image is transformed into wavelet coefficients using the 2-level discrete wavelet transform (DWT). The wavelet Db1 is employed here. All the coefficient sub-bands in the DWT domain are shown in Fig.7 (a). They are the lowest frequency sub-band (LL2), the mid-frequency sub-band (LH1, HL1, LH2 and HL2), and the high-frequency sub-band (HH1 and HH2). The lowest frequency sub-band LL2 concentrates the most

LL2	LH2	LH1
HL2	HH2
HL1		HH1

(a)

Figure 6. The host image, the original watermark and the scrambled watermark.

Watermark W

Reconstruction of

Wavelet Coefficients

Watermarked

Image H'

Host Image

H

Decomposition of

Wavelet Coefficients

LH2

Restoration

LH2'

Scrambling the

2 X 2 Blocks       ^Embedding

HL2

Restoration

HL2'

Vector W1

Vector

W2

Scrambling

Image W'

Rearran ging

Vector W''

Dividing into

2 Vectors

(c)

Figure 7. Wavelet coefficients and strategy for embedding the watermark. (a)Wavelet coefficients at 2-level DWT; (b) Positions for embedding the watermark information ; (c)Strategy for embedding the watermark.

The scrambled watermark W ' is arranged to be a vector W " of size 1 x 4096, and W " is divided into two

vectors W_v = W "(0:2047) and W = W "(2048:4095) . They are respectively embedded in medium frequency sub-band LH2 and HL2, which are both of size 128 by 128.

To embed the watermark bits, both LH2 and HL2 are divided into non-overlapping blocks of size 2 by 2, so as to form matrices with 64 x 64 blocks. Then, the blocks in this two sub-bands are scrambled 12 times respectively with the proposed scrambling algorithm, and two new matrices LH2’ and HL2’ with 64 x 64 blocks sized 2 by 2 are derived. The intercepted blocks of LH2’ are shown in Fig.7 (b), and the watermark bits will be embedded in the location marked by gray color. The strategy to embed the watermark bits is shown in Fig.7 (c).

The watermark bits in W are embedded in the left

part of sub-band LH2’ with 64 x 32 blocks. The order to embed is from top to bottom and then from left to right. The watermark bits in W are embedded in the right part

where u (x, y) = round( f (x, y) ) ,             (8)

a • m ( x , y )

v ( x , y ) = mod( u ( x , y ), 2),            (9)

f (x, y) = u (x, y) • a • m (x, y), in which a = 0.07 is used. If the watermark bits of vector

W (or W ) are all embedded, all the coefficients in LH2’ (or HL2’) should be subtracted with d . Then, the inverse discrete wavelet transform is employed to get the watermarked image.

After embedding the scrambled watermark image (Fig. 6 (c)) in the host image (Fig. 6 (a)), we can get the watermarked image shown in Fig. 8 (a). The value of peak signal-to-noise ratio PSNR is used to evaluate the quality of a watermarked image. The greater the value is, the lower the visibility of watermark images is.

of sub-band HL2’ by the same order. Then the blocks in LH2’ and HL2’ are restored 12 times respectively by the inverse scrambling algorithm. Finally, all the sub-bands are reconstructed into an image by the inverse wavelet transform and the watermarked image is yielded.

The watermark bits are embedded according to the following steps. The bit w in W (or W ) is supposed

to be embedded into LH2’(or HL2’ ).

(i) Add parameter d coefficients in LH2’ (or positive.

calculated by (6) to all the

HL2’) so that they are all

Var d =

128 x 128

• k,

where Var is the variance of all the coefficients in the

(a) Watermarked image (PSNR=47.2)

(b) Extracted Watermark

corresponding sub-band LH2’ (or HL2’). k is a controlling parameter. In the experiment on the host image LENA and the watermark STU, if the sub-band is LH2’, we set k = 61 while if the sub-band is HL2’, we set k = 7 .

(ii) Compute the neighbor mean value m ( x , y ) of the coefficient f ( x , y ) , which is used to embed the watermark bit:

m ( x , y ) = f ^{( x} — 1, ^y ) ⁺ f ^{( x} , y '' ⁺ f ^{( x -} 1, ^{y - 1)}   (7)

where x , y = 1,3,5,...,127.

(iii) If w is 1, then

f ( X , y ), if v ( x , y ) = 1

f '( X , y ) = ■

[ u ( x , y ) - 1f a • m ( x , y ), if v ( x , y ) = 0, f ( x , y ) <  f ( x , y )

[ u ( x , y ) + 1f a • m ( x , y ), if v ( x , y ) = 0, f ( x , y ) >  f ( x , y )

otherwise,

f ( x , y ), if v ( x , y ) = 0

f '( x , y ) = ■

[ u ( x , y ) - 1f a • m ( x , y ), if v ( x , y ) = 1, f ( x , y ) <  f ( x , y )

[ u ( x , y ) + 1] ^ a • m ( x , y ), if v ( x , y ) = 1, f ( x , y ) >  f ( x , y )

(c)Restored watermark (NC=1)

Figure 8. The watermarked image and extracted watermark.

The process to extract the watermark is similar to that to embed the watermark bits. The watermarked image is transformed into wavelet coefficients using the 2-level DWT. The sub-bands LH2 and HL2 are respectively divided into non-overlapping blocks of size 2 by 2. The blocks in either LH2 or HL2 are scrambled 12 times by the scrambling algorithm to obtain two new matrices LH2’ and HL2’; and the watermark bits can be extracted according to the following steps.

• (i)    Calculate the parameter d by (6) and add it to all the coefficients in LH2’ (or HL2’), so that all the coefficients in the corresponding sub-band are positive.

• (ii)    Compute the neighbor mean value m ( x , y ) of coefficient f ( x , y ) with (7), where x , y = 1,3,...,127 .

(iii) Denote the watermark bit in W (or W ) as w ' ,

and calculate v ( x , y ) by (8)- (9). Then let

w' = <

1,

if v (x, y) = 1,

_0, if v(x, y) = 0.

Repeat Steps (ii) ~ (iii) till all the bits of W and W are extracted.

The extracted watermark information and the restored watermark are shown in Fig. 8 (b)-(c). Another value normalized correlation NC is used to judge the existence of the watermark [19]. If NC = 1 , the extracted watermark is the same as the original watermark. In Fig.8, the watermarked image has low visibility, and the watermark is completely extracted with NC = 1 .

		^^^^
(a) 1/4 area cropping at upper-left corner PSNR=12.01 NC=0.546	(b) 1/4 area cropping at upper-right corner PSNR=10.95 NC=0.543	(c)1/2 area cropping at Left side PSNR=9.73 NC=0.349
^ ^^^^ ^	5^Ш|	№Й
(d) 1/2 area cropping at Right side PSNR=7.93 NC=0.246	(e) JPEG compression (Q=80) PSNR=38.11 NC=0.932	(f) JPEG compression (Q=65) PSNR=36.61 NC=0.792
^^^^^^^	ИЙ
(g) JPEG compression (Q=50) PSNR=35.65 NC=0.549	(h) Wiener filtering ( 3 x 3 ) PSNR=37.52 NC=0.645	(i) Median filtering ( 3 x 3 ) PSNR=35.39 NC=0.545
ВЯ M		Ий
(j)Gaussian filtering ( 3 x 3 ) PSNR=40.29 NC=0.707	(k)Add pepper & salt noise (intensity=0.5) PSNR=28.35 NC=0.626	(l)Add Gaussian noise (intensity=0.03) PSNR=34.98 NC=0.693

Figure 9. The watermarks extracted from the attacked watermarked image.

The parameter k and a are the keys in this watermarking. In addition, times for scrambling the original watermark and the blocks of coefficients in LH2’ or HL2’ can also be considered as the keys. The watermarks extracted from the attacked watermarked image are shown in Fig. 9.

• V. CONCLUSIONS

In this paper, the standard 3D Baker map is improved by both tent map and double map. The improved map is projected on xy plane so as to obtain the itineraries of the image pixels, which uniformly distribute in a unit square by iteration. The itineraries are used to encode the positions of digital image pixels, and then the codes are applied to scramble a digital image. Simulation shows that the scrambled image has strong robustness against various kinds of attacks. Finally, the scrambling algorithm is applied to preprocessing in a watermarking strategy. The watermarking scheme embeds the scrambled watermark bits into the DWT mid-frequency sub-band of the host image according to the odd-even adjustment rule and the neighbor mean value. The strategy also shows that it is efficient in resisting various kinds of attacks and the watermarked image looks visually lossless.

Acknowledgment

We thank anonymous referees for their constructive comments. This research was supported by National Natural Science Foundation of China (No. 11071152) and Natural Science Foundation of Guangdong Province (No. 10151503101000023).