Барометрический эффект нейтронной компоненты космических лучей на антарктической станции «Мирный» с учетом ветра

При исследовании вариаций первичного космического излучения очень эффективными являются такие прецизионные детекторы, как нейтронные мониторы. Так, статистическая точность стандартного нейтронного супермонитора 18-NM-64 на уровне моря при часовом усреднении составляет ~0.15 %, поэтому необходимо обеспечить уровень прочих возможных ошибок не хуже этой статистической ошибки. К таким возможным ошибкам относятся ошибки, связанные с исключением барометрического эффекта из данных наблюдений. Типичная точность современных датчиков давления 0.2 мбар, что дает нам требуемую точность поправок ≈0.15 %. Однако имеется еще одно, более трудно учитываемое обстоятельство. Барометрический эффект, который в первую очередь обусловлен поглощением нейтронов в атмосфере, определяется количеством вещества над детектором, т. е. статическим давлением. Применяемые датчики давления измеряют полное давление как сумму статического и динамического давления. Задачами настоящей работы являются экспериментальное определение вклада динамического давления и введение необходимых поправок в данные наблюдений.

Динамическое давление обусловлено ветровым потоком и равно кинетической энергии единичного объема вещества:

PD=½ρV2, где ρ — плотность воздуха, V — скорость потока. Однако только часть кинетической энергии CxPD преобразуется в потенциальную энергию и воздействует на препятствие и в конечном счете на показания датчика давления. Коэффициент пропорциональности Cx, или аэродинамический коэффициент, зависит от геометрии препятствия и числа Рейнольдса. Влияние ветра для отдельных событий исследовалось ранее [Lockwood, Calawa, 1957; Dubinsky et al., 1960; Kawasaki, 1972; Buticofer, Flugiker, 1999; Dorman, 2004]. Обзор этих работ сделан в книгах [Дорман, 1972; Dorman et al., 1999]. Однако детальный анализ динамического эффекта ветра, включающий антарктические станции, где наблюдаются очень сильные стоковые ветра, не проводился.

ИСПОЛЬЗУЕМЫЕ ДАННЫЕ

Регулярный мониторинг космических и метеорологических параметров на ст. «Мирный» осуществляется с 2007 г. Анализ проводился на базе данных с часовым разрешением, исправленных на барометрический эффект по классической методике [Kobelev et al., 2011], с привлечением скорости счета нейтронного монитора 12-NM-64. Для оценки турбулентности потока привлекались также данные по атмосферному давлению и скорости ветра с минутным разрешением.

На антарктических станциях, в том числе и на ст. «Мирный», в связи с особенностями рельефа наблюдаются стоковые ветра. Максимальной силы стоковые ветра достигают антарктической зимой — с апреля по ноябрь они дуют почти непрерывно. На рис. 1 приведена наблюдаемая скорость ветра за 2007–2014 гг. с минутным разрешением.

ИСПОЛЬЗУЕМЫЙ МЕТОД

Барометрический эффект легко исключается на основе закона поглощения излучения в атмосфере по отклонению измеренного атмосферного давления (предполагается, что это статическое давление P S ) от стандартного P 0 для данного пункта наблюдения:

N C = N U exp[–β( P 0 – P S )], (1)

где β=1/μ — так называемый барометрический коэффициент, μ — пробег частиц в атмосфере, N U — измеренная скорость счета детектора, N C — скорость счета детектора, приведенная к стандартному уровню P ₀.

Поскольку измеряемое применяемыми датчиками барометрическое давление P есть сумма статического и динамического давления в данной точке атмосферы, то статическое давление равно разности измеренного и динамического давления, т. е. P–C x P D .

Исправленную на барометрический эффект (давление статическое) скорость счета детектора N С можно представить как

N C = N U e ^{-e [} P 0 - (^{P -} C x P D )] =

= N u exp( -p ( P o - P )) exp( -p -P D ) ,            (2)

'--------------------------------------V---------------------------------------'

0 NC где P0 — среднее давление на временном интервале. Барометрический коэффициент β>0 (для ст. «Мирный» β=0.73 %/мбар, P0=980 мбар) определяется в спокойный и безветренный период. Логарифмируя уравнение (1) и перенося слагаемые с неизвестными в правую часть, получим

In N- = In NC +p CxPD, или y = a + cx, где y = InNC, a = InNC, x = PPD, т. е. линейное относительно a и c уравнение регрессии.

Коррекция данных на первичные вариации

При решении задачи оценки барометрического эффекта измеряемую скорость счета детектора N_U нужно освободить от первичных вариаций [Dorman, 1974; Крымский и др., 1981; Kobelev et al., 2013]. Это можно сделать, если N U заменить на

Nu /(1 + v), где ν — первичные вариации для данного пункта. Последнее выражение следует из определения вариации v = (NU - NB)/ NB. Тогда уравнение (2) запишется как

N c = N u / (1 + v ) exp ( -P ( P _o - P )) exp( -p C x P D ). (3) N C ⁰

В приближении нулевой гармоники первичные вариации можно исключить по данным опорной станции S следующим образом. Запишем вариации для двух детекторов как v = a ₁₀ C ₀ и v ^s = a ₁₀ C, f , где С 0 и C ₀ ^S — приемные коэффициенты ст. «Мирный» и опорной станции соответственно.

Освобождаясь от неизвестной амплитуды нулевой гармоники а10, получим v = vs    .                                          (4)

S

C ₀

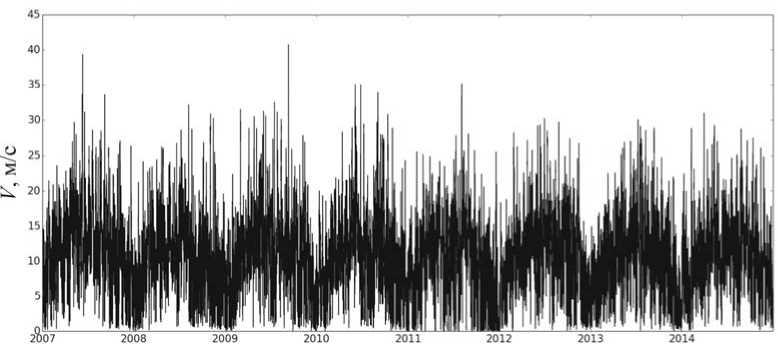
Рис. 1 . Скорость ветра на ст. «Мирный»

Выражение (4) учитывает различие параметров станций (высоту, жесткость геомагнитного обрезания) и, в принципе, позволяет привлекать любую станцию в качестве опорной. В данной работе в качестве опорной была использована ст. «Оулу».

Корректное решение вопроса учета первичных вариаций важно, поскольку станция, данные которой используются в анализе, высокоширотная. Амплитуда первичных вариаций для нее велика и часто может быть сопоставима с величиной барометрического эффекта, если учесть, что рассматриваемый временной интервал составляет несколько лет (2007–2014 гг.).

ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ

Для анализа было выбрано около десятка событий, когда наблюдавшаяся скорость ветра превышала 30 м/c. Для примера приведем событие сентября 2009 г., когда максимальная скорость ветра достигала 42 м/c. На рис. 2 показана корреляция между скоростью счета и вычисленным динамическим давлением P D . Скорость счета (серые кружки) по изложенной выше методике (формула 4) была скорректирована на первичные вариации (черные кружки). Корреляционный анализ для этого события приводит к аэродинамическому коэффициенту C x =0.63±0.03, коэффициент корреляции равен 0.93 (значение коэффициента корреляции до корректировки данных на первичные вариации 0.91). Для данного события коэффициент корреляции оказался наилучшим.

Строго говоря, аэродинамический коэффициент зависит от значения числа Рейнольдса, которое пропорционально скорости ветра. Однако в ограниченном диапазоне рассматриваемых скоростей такой зависимостью можно пренебречь, если оцениваемые нами числа Рейнольдса находятся вне критической области сопротивления [Шакина, 2013].

Детали анализа представлены на рис. 3. На верхней панели изображены временные зависимости исправленных на барометрический эффект скоростей счета без учета и с учетом влияния ветра, а также значения скорости ветра. Четко видна антикорреляция скорости счета детектора N _C ⁰ и скорости ветра, которая полностью снимается после коррекции

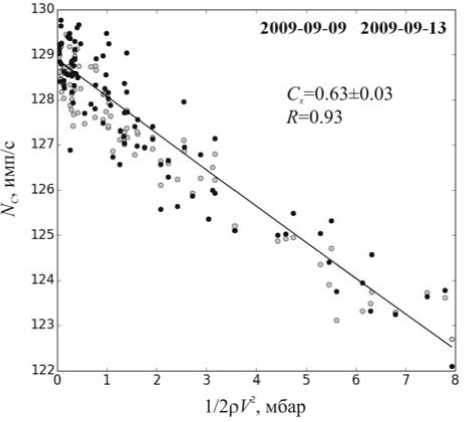
Рис. 2 . Корреляционная зависимость не исправленной и исправленной на первичные вариации скорости счета (серые и черные точки соответственно) от динамического давления ветра, кривая — аппроксимация методом наименьших квадратов исправленных данных

на динамический эффект в соответствии с выражением (4). На средней панели представлены временная зависимость скорости ветра (с минутным разрешением) и результат обработки фильтром первых разностей. Видно, что при скоростях ветра более 15 м/c возрастает турбулентность потока; этот факт следует учесть при проведении дальнейших исследований. На нижней панели — показания двух датчиков давления и их разность (минутное разрешение). Согласно этим результатам показания разнесенных в пространстве (~900 м) датчиков давления идентичны в слабоветреные периоды и флуктуируют при больших скоростях ветра, что подтверждает турбулентность потоков. Турбулентность, наблюдаемая для свободного датчика давления P M , меньше, чем в случае датчика давления P в здании, что связано с условием обтекания здания воздушным потоком.

Полученные аэродинамические коэффициенты C x позволяют учесть динамический эффект для всего периода наблюдений, что показано на рис. 4, где ν cor. — вариации космических лучей после поправок на динамическое давление. Если учесть, что точность 73

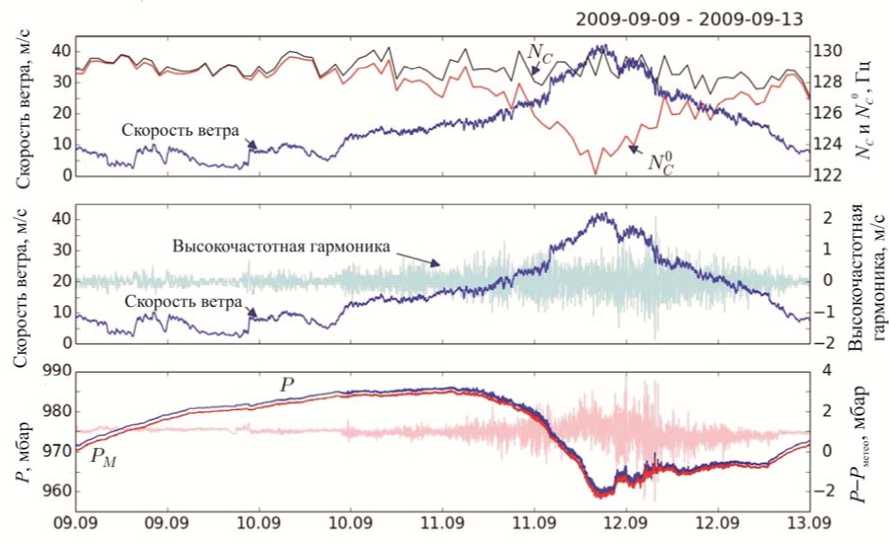
Рис. 3 . Временные зависимости исправленных на барометрический эффект скоростей счета без учета и с учетом влияния ветра ( N _C ⁰ и N_C ), а также значения скорости ветра (верхняя панель). Временная зависимость скорости ветра с минутным разрешением и результат обработки фильтром первых разностей (средняя панель). Показания двух датчиков давления и их разность (нижняя панель)

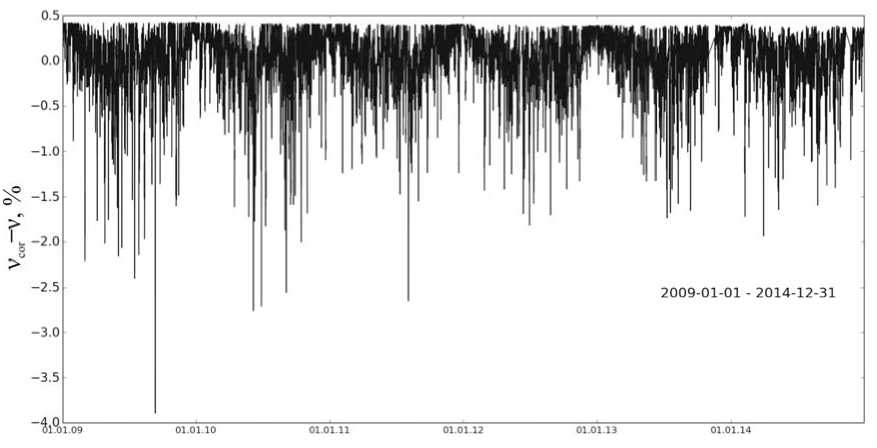
Рис. 4 . Поправка на динамический эффект для наблюдаемых вариаций космических лучей для периода 2009–2014 гг.

наблюдаемых вариаций — десятые доли процента, то возможная ошибка за счет динамического эффекта, как следует из рис. 4, при сильных ветрах достигает нескольких процентов.

ВЫВОДЫ

Показано, что на ст. «Мирный», где скорости ветра часто достигают больших значений, абсолютная ошибка в определении вариаций может достигать 2– 4 % и, таким образом, для получения точных данных всегда необходимо проводить перерасчет барометри- ческого эффекта с учетом динамического эффекта ветра. Для выявления зависимости аэродинамического коэффициента от числа Рейнольдса необходимо увеличить число рассматриваемых событий и расширить диапазон рассматриваемых скоростей ветра. Кроме того, очень важно рассмотреть динамические эффекты для других полярных детекторов, в первую очередь для нейтронного монитора «Маусон», где наблюдаются самые большие регулярные ветровые потоки. Очень важно также привлечь данные горных детекторов, для которых существуют совершенно другие условия обтекания препятствий.