Bayesian approach to generalized normal distribution under non-informative and informative priors

The generalized normal (GN) distribution, also known as power exponential, exponential error or generalized Gaussian distribution extends the normal distribution by adding a shape parameter. Being a generalization of the normal and Laplace distributions, this distribution is perhaps the most widely used in areas such as signal processing, quantitative finance, medicine, telecommunication, information systems, physics, analytical chemistry, cybernetics, energy and fuels, biology, nanotechnology, neurosciences, operations research and management science, reliability and risk. Additionally to the mean and variance, the GN distribution has the shape parameter p , which is a measure of the peakedness of the distribution, however, it seems that there is not a closed-form expression for estimating p .

* Corresponding author.

Various generalizations of the normal distribution are in use. The most well-known among them appears to be that proposed by Nadarajah (2005); his version alters the kurtosis, adjusting the sharpness of the peak, but maintains a zero-skew symmetry. Varanasi and Aazhang (1989) discuss parameter estimation for the GN distribution by using the methods of maximum likelihood and moments. Box (1973) first discussed its characters as well as the Bayes inference. GN distribution has been widely adopted in signal processing. Gharavi and Tabatabai (1988) adopted it to approximate the marginal distribution in image processing.

A random variable X is said to follow a (GN) distribution if its PDF is given by

—

ц

x ; ц , о , p ) =--------- ее ^о ; x е R

"         !  2 о Г(1/p)

where the parameters ц , p >  0 denote the mean and shape parameters of GN distribution respectively, о is the standard deviation of the GN distribution. The shape parameter p denotes the rate of decay: the smaller p , the more peaked for the PDF, and the larger p , the flatter for the PDF, so it is also called as the decay rate. In most of the applications the mean can be considered as zero, i.e., µ = 0, then we will be focused on estimating the parameter of the GN distribution with two parameter.

For p = 1 , GN distribution reduces to Laplace or double Exponential distribution, for p = 2 , GN distribution reduces to Normal distribution and for the limiting cases of p, we can obtain a distribution close to the uniform distribution as p→0. Like the normal distribution, equation (1) is bell-shaped and unimodal with mode at x=ц. Furthermore, f (ц) =

p

.

2 о г ( 1/ p )

The GN distribution is symmetric w.r.t. μ , hence the odd order central moments are zero; i.e.,

E ( X — ц ) r = 0 ; r = 1,3,5...

Let ц = 0 and let Y = | X — ц | = X , then the PDF of Y is given by

f ⁽ y ; ° , p ) =

p_e ^о Г ⁽ 1/ p )

—

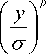
; y >  0.

The factor 2 in the denominator vanishes to make Y > 0. Thus the absolute moments of X are given by

EXT = E (y)r

о r(1/ p)

to

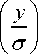
dy

; r >  0.

^p y Put I ^ y I l о)

— 1

p

Also, as y >  0 so is z >  0.

Therefore, we get

r

EX  = E ( У ) r =       rl r + 1 I .                                                                  (4)

^{Г( 1/} p ⁾   ( p )

The variance of X is given by putting r = 2 in (4) and is given by

v„ (X)= E [X - E (X)]2 = E (X — Д = E (r)2 = a 2 Г(3./

The expectation is still μ but variance depends on the shape parameter p and decreases with respect to p. The CDF of GN distribution is given by

У I p

—

F ( y ; a , p ) =              I ' ^ dy

а Г(1/ p) J yp

1       ^a p

=—¹— e - ^— z Г ( 1/ p ) ^J

1—1

z^p dz = —1-—\Y I ¹, — I .

Г ( 1/ p ) ^ p a^{p J}

In addition to the complementary incomplete gamma function mentioned above, the calculations in this paper use the Euler’s psi function defined by ^(x) = — logГ(x). This special function can be found in dx

• 2.    Maximum Likelihood Estimation

Maximum Likelihood Estimation (MLE) method is the general method of estimating the parameters of a statistical model given observations, by finding the parameter values that maximize the likelihood of making the observations given the parameters. To obtain the MLE of a and p , we assume that X = ( X_Y , x₂ ,..., X_n ) is a random sample from GN ( a , p ) defined in (3), then the likelihood function of a and p is given by

L = L ( a , p | x ) =

pn

[a r(1/ p)]

e

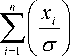
p

and the log-likelihood is given by l = ln L = n ln p — n ln Г(1/p) —

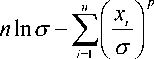
Then the MLE of a and p is obtained by the solution of the equation

—

^p

I = 0

л

ⁿ

' У x'

. n И

^p

which depends on the shape parameter p .

n ^p

And 1 + -^(1/p) — ' Ц , | In I , | = 0 p         n^ V ст) V ст)

Substituting the value of a from (8), we get

n

I x i^P ln x i

^{1 +} - ^ ⁽ 1/ p ^{) —} ^=1^------

= 0.

'         I x .'

i = 1

Equation (9) can be solved by the iteration method of Newton-Raphson using

P k + 1 = P k

^

f ('k) f‘('k)

where f ( p_k ) is denoted by (9) and

n

n

f'('k ) = — ^2 W p) — -13 v\1! p) —

I x' (ln x^  I

7 2

xi ' ln x i

p

p

i =1 __________________

ⁿ

p

1 1 x i I

V i = 1      7

—

V

i = 1

n

I x.'

i = 1

n

I V ^{ln x}t

+ —---- n i=1

—

⁺ 7

where ^ ( z )₌E_( z_ denotes the digamma function 1/7 '( z )

denotes the trigamma function. Thus p ˆ is obtained

by choosing the initial value of p_k and iterating the procedure till it converges. When p is obtained, CT can be obtained from (8).

• 3.    Fisher Information of GN Distribution

For estimation procedures, the Fisher information matrix for n observations is required. It is used in the asymptotic theory of MLE and Jeffreys prior The second-order derivatives of equation (7) are:

d ⁵ 2 1 and — z- =

—

p

n

a2

2n d 1 _p y

i = 1

—

^p

^p

a ²

i = 1

i = 1

^,

^p

^,

^p

.

Now, since X ~ GN ( a , p ) , given in (3), we have the following results:

x ) p

r

—

E

e ^{к a ;} dx

X ( r + 1 )

=      f z^

Г(1/p )J

-—1

¹ 1 e — z p

dz =

r ( r + 1/ p )

Г ( 1/ p )   ’

г Г x : r i Г x

E I I ln l — к a ) к a

X

=

pr(1/ p )l

( r ± 1 )_— 1 z^p

e ^z ln zdz

_ r ( r + 1/ p ) _ ^{r( r} + 1/ p ) /—  \

= pГ(1/p)  = pГ(1/p) ^(r + 1/p), r x and EI I ln к aJ

2 1 x

^f p ^{Г( 1/} p ) 0

( r ^{+ 1 )} z^p

-—J

e ^z ln ² zdz

=4+1/p)=гlr+1/p) [^ 2 (r+1 / p)+^,(r+-1/p)]. p2г(1/p)   p2г(1/pГ V      7 V

The elements of the Fisher information matrix are, therefore, given by:

E

—

к

np

f

E

к

d21)

5 p da _y

—— [1 + y(1 +1/P)], Pa

and E [-^ L к dP 2J PP

1 + - y ^{( 1/} p ) + ' y^{, ( 1/}p ) +- ^{y ^{2 (} 1 + 1/ p ) + ^ '( l + 1/ p ^)} . PPP   _

Thus, the Fisher information matrix is given by:

np + 2 y(1/p) + - y'(1/ P) + у2 (1 + 1/P)

I ^a p ) =^        ^p

_        +y'(1+1/p )-{1+y(1+1/p )}2

n ²

^a p

p + 2y(1/ p) + — y'(1/ p) + y'(1 +1/ p)-1 - 2/(1 +1/ p) p

Using the following results: y ( 1 + x ) = y ( x ) +— and y '( 1 + x ) = y '( x ) .

x                       x ²

We have

I(a, P )

n ²

^a P

1 + - y'(1/P )-P (P + 1) к P J

• 4.    Lindley Approximation of α and p under Jeffreys Invariant Prior

  Bayesian approximation has found good sources provided by the works by Ahmad et.al (2007, 2011) discussed Bayesian analysis of exponential distribution and gamma distribution using normal and Laplace approximations. Sultan and Ahmad (2015) obtained Bayesian estimation of generalized gamma distribution using Lindleys approximation technique for two parameters. Fatima and Ahmad (2018) studied the Bayes estimates of Inverse Exponential distribution using various Bayesian approximation techniques like normal approximation, Tierney and Kadane (T-K) approximation methods.

The GN distribution has not been discussed in detail under the Bayesian approach. Our present study aims to obtain the Bayesian estimators for the shape and scale parameter of the GN distribution based on Lindley approximation technique. A simulation study is also discussed with concluding remarks.

For a Bayesian analysis of the GN distribution, we can use different prior distributions for the model parameters a and p . The Jeffreys invariant prior (Box and Tiao (1973)) and Gelman et al. (1995) for a and p is given as:

g (a, P )=[det I (a p)]1/2

where I ( a , p ) is the joint Fisher information matrix defined in (13). Thus, the Jeffreys invariant prior for a and p is given by:

( A   V A ⁽ P )

g ^{( т} , p )^------

T p where A (p)

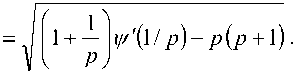
Then the joint posterior distribution of t and p is given by

n (t, p | x )да L (x | t, p )x g (t, p)

n ^p

_ V I x i I

K p" -1 M p ) e - I T J

Tn+1 [г(1/ p)]"

where K is a normalizing constant defined as

K

- 1

да да

=jj

p" ^{- 1} >№)

T+1 [Г(1/ p)]"

—

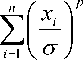
These integrals cannot be simplified in to a closed form. However, using the approach developed by Lindley (1980), one can approximate these Bayes estimators in to a form containing no integrals. This method provides a simplified form of Bayes estimator which is easy to use in practice. The basic idea in Lindley approach is to obtain Talyor Series expansion of the function involved in posterior moment. Lindley proposed the ratio for obtaining Bayes estimates as

E [ h ( 0 ) | x ] =

J e^{L ( 0} ) g ( 0 ) d 0

E [h (0) | x] =

^{< h + 1} yS h iy ^{+ 2} hi ^ j^ ^ y

² i j

+ -

ЕШ LjkMJ + O

i jkr

where i , j , k , r = 1,2,... m ; 0 = 0 , 0 ,... 0

h - —h , hi - ^{д L} , L_ljk - —^- L , р - р ( ^ ) - log [ g ( 0 ) ] , р - ^др

‘   д0    ^j д0д0 ^j    д9 i д0 j д9_к                   ^v      i 50

and ф_i j is the ( i,j ) th element in [ L_tJ ] ¹

For two parameters case m = 2, we have

L -^2-

²⁰ до e

о2

n —

p

L =^3-

³⁰ d e³

о 3

— 2 n +

p ⁽ p ⁺ 1 ⁾⁽ p ⁺ 2 $ ( a ⁾   •

L =^3L

²¹    д p д о²

p

p

and

Hence, ф^ -

and

L 03

L =^2 l ⁰²     д p²

^L 20

— 1

—

"n ⁺ 2 3 V ( 1/ p ^{) +} - n r V ’

pp

p

( 1/ p ) — $ ( e ) p v ( e )•

д ³ 1

дp3

L

^ф 22

2 n 6 n         6 n

= — ⁺— V ^{( 1/} p ⁾⁺ —

pp

p

v '⁽i/ p ⁾⁺ n 6 ^v v "⁽i/ p ^)— $$ ^ xi^ ^{) ln} 3 ^ xi^ ⁾

- д³ 1

²¹    до д p²    о

^л о

—

n —

— 1

^L 02

2 $ ( e ) p -( e )— $ ( e ) ^p - ( e )

p

n 2 n / x n

= — + — V (1/p) + — V

p

— 1

pp

p

• с/ p ) — $ ( e ) ^p -( e ) .

and,

Р = ln g ( о , p ) = — ln о — ln p + ¹ In [ A ( p ) ]

■ .       1               1 A '( p )

.. p _x =-- and P 2 =-- + ^v

7         p 2 A (p)

where A ' ( p ) = — ± V^H p ) + ^f 1 + - И/ p ) — ( 2 p + 1 )

p -          V p J       _

When h (7, p) = 7 ^ h = 1, hn = h2 = h22 = 0 , the Lindley approximation for 7 under Jeffreys prior is obtained as

f— 2 n +

p

л

2 +

i = 1 V ¹

p

n—

E (71 x) = 7

1 +

p

i = 1

n —

i = 1

—

22f  1 p inf“1 — 2f  1P ln2f12 V 71 V 7 J 2 V 71    V 7г1

n   2 n          n

._? ⁺ tj V ^{( 1/} P ^{) +} tj V

p

.

V

p

p

p

i = 1

J 7

When h (7, p) = p ^ h2 = 1, h22 = h21 = hn = 0 , informative prior is obtained as the Lindley approximation for p under the non-

1 + 4y V,(1 /p)+ V "(1/ p)+ (2 p +1) pˆ   pˆ 2

^f 1 + 4 V ^,(1/ p ) — p ⁽ p + 1 )

V p J

E ( P I x ) = ^p + -

2 n 6 n         6 n

⁺ ^4 V ^{( 1/} P ^{) +} ^5

pp

⁺        г

p

p ˆ

V'(1/p)+p-V"(1/p) 27J in3 V7J

+

n   2 n          n

-ту +   V\1/p) + V pˆ    pˆ            pˆ

^{( 2 p} + 1 ) E ^f x^ 1 ^{— p ( p}

ˆ

' (1/p ) —tf x^ 1 in2 f x^ 1

7=1 V °r J     V °r J n          pˆ

i = 1

ˆ

n—p (p+1)2^ X[ 1

4r ⁺ 2" V ^{( 1/ p ) +} n^ V 'I

pp

p

ˆ

( 1/ p ) — t f x ^ 1 in² f x ^ 1 V o- J V c r J

.

• 5.    Lindley Approximation of α and p under Uniform and Gamma Prior

Assuming that 7 has a Uniform prior density given by

g (7) = 1,7 > 0

and p has gamma prior with known hyper-parameters a and b given as

g(p )=

—(

a a—1

pa e

r( a )

p b, p > 0, a, b > 0.

Then the joint prior density is defined by

p g (7,p)^ pa—1 e b.

The joint posterior distribution of 7 , p is given by

ⁿ 2 ( ⁷ , P I x ) « L ⁽ x I ⁷ , P ^)x g ( ⁷ ,P )

—

n + a — 1

= K—p---^e

7 ⁿ [ Г ( 1/ p ) ] ⁿ

where K is a normalizing constant defined as

—

n ^p

E l xi I    p

I I +

, = 1 I 7 J     b

to to

K 4=d

p « + a — 1

7П [Г(1/p)]П

e

p

+ p

^J d 7 dp.

p

Again, g ( 7 , p ) to e ^b p a ^—1

л p = ln g (7, p ) = ln 7 + (a — 1) ln p — -p

^ P = 0 and a — 1 1

^p 2 =---

When h (7, p) = 7 ^ h1 = 1, hu = h2 = h22 = 0, the Lindley approximation for 7 under uniform prior is obtained as

(

^p

—

^p

E (с | x) = C

+

^p

^p

^p

.

_—

n   2 n          n

■ 2 ⁺    V ^{( 1/} p ^{) +} ТГ

^p

к p p

^p

7

When h ( с , p ) = p ^ h₂ = 1, h₂₂ = h = h_u = 0 , the Lindley approximation for p under the gamma prior is obtained as

—

1 a — 1 ■           .■

b

2 n 6 n          6 n

^3 ⁺ -T4 V ^{( 1/} p ⁾⁺ -T5

pp

^p

V '^{(1/ p ) +} n^ p ˆ

p ˆ

^A

+

n   2 n         n

• -ту ⁺    V ^{( 1/} p ⁾⁺

pp

fxL)p —

p pˆ

n

p ˆ

E ( p | ^x ) = ^p +-

ⁿ

• ² n ^{— p ( p +} Щ

к C

i = 1

n 2 n         n

• -ту ⁺ -tj V ^{( 1/} p ⁾⁺

pp

^p

p ˆ

p ˆ

.

• 6.    Simulation Study

  The simulation study was conducted in R-software using the pgnorm package to examine the performance of Bayes estimates for the shape ( p ) and scale ( σ ) parameter of the generalized normal distribution under Jeffreys invariant prior and informative (Uniform and Gamma) prior using Lindley approximation technique. We choose n (= 20, 60, 100, 150) to represent different sample sizes, in each sequence of the ML estimates and Bayes estimates for the given values of p = 1, 2, 4 and σ = 2, 4, 6 the desired ML and Bayes estimates are presented in Tables 1, 2 and 3. The hyper-parameter values are chosen a = (1, 1.7, 2.5) and b = (2, 3, 3.5). The estimators are obtained along with their respective MSE. The results are replicated 5000 times and the average of the results has been presented in the tables below.

• 7.    Discussion

• 8.    Conclusion

Table 1. ML Estimates and MSE of p and σ
n	p	σ	А p ˆ	MSE ( p ˆ )	А σ	MSE ( σ ˆ )
	1.0	2.0	1.70180	1.035623	4.26663	7.13999
20	2.0	4.0	3.00955	6.12246	5.50290	4.17824
	4.0	6.0	1.74799	5.88624	5.36854	4.27863
	1.0	2.0	1.43941	0.33298	2.97165	1.46411
60	2.0	4.0	2.21905	0.55855	5.63489	3.56623
	4.0	6.0	4.60557	2.67606	8.23932	5.44743
	1.0	2.0	1.03299	0.04012	1.82053	0.28776
100	2.0	4.0	3.33154	2.73334	7.19524	10.6439
	4.0	6.0	3.81543	0.92509	8.86350	8.61033
	1.0	2.0	1.04799	0.02344	2.01891	0.16495
150	2.0	4.0	2.33422	3.52167	5.86343	3.75382
	4.0	6.0	3.98795	0.92848	8.41659	6.11403
Table 2. Estimates of p and σ		under Jeffreys Prior
n	p	σ	p ˆ	MSE ( p ˆ )	А σ	MSE ( σ ˆ )
	1.0	2.0	1.84972	1.26512	2.07642	2.00822
20	2.0	4.0	3.77079	8.23897	4.05533	1.92259
	4.0	6.0	3.54917	1.01794	6.02304	3.88042
	1.0	2.0	1.09269	0.14849	2.03379	0.52115
60	2.0	4.0	2.00275	0.51058	4.00861	0.89343
	4.0	6.0	3.85749	2.32965	6.00642	0.43292
	1.0	2.0	1.05165	1.05432	2.02979	0.25644
100	2.0	4.0	1.98551	0.96055	4.00205	0.43434
	4.0	6.0	3.95455	0.89309	6.00232	0.41071
	1.0	2.0	1.04945	0.02359	2.01487	0.16481
150	2.0	4.0	1.99519	0.16898	4.00366	0.28146
	4.0	6.0	3.95352	0.93049	6.00168	0.27412

Table 3. Estimates of p and σ under Gamma and Uniform prior

n	p	σ	p ˆ			MSE ( p ˆ )			А σ	MSE ( σ ˆ )
			a=1 b=2	a=1.7 b=3	a=2.5 b=3.5	a=1 b=2	a=1.7 b=3	a=2.5 b=3.5
	1.0	2.0	1.62803	1.71924	1.80844	0.93752	1.06041	1.19668	2.04116	2.00407
20	2.0	4.0	4.93438	4.56135	4.23818	13.7139	11.6638	10.1127	4.02277	1.92005
	4.0	6.0	4.25978	4.10167	3.98708	0.88218	0.82503	0.81486	6.00434	3.87991
	1.0	2.0	1.05226	0.14263	1.08517	0.14263	0.87498	0.14715	2.01697	0.52030
60	2.0	4.0	2.13753	2.09432	2.05689	0.52948	0.51947	0.51381	4.00344	0.89337
	4.0	6.0	4.10005	4.04608	4.00696	2.31935	2.31146	2.30939	6.00135	0.43288
	1.0	2.0	1.02783	1.03763	1.04721	0.03980	0.04045	0.04126	2.01371	0.25574
100	2.0	4.0	2.04208	2.02394	2.00823	0.96211	0.96091	0.96041	4.00074	0.43434
	4.0	6.0	4.01342	4.00032	3.99083	0.89120	0.89102	0.89110	6.00047	0.41070
	1.0	2.0	1.03025	1.03815	1.04588	0.02206	0.02260	0.02324	2.00721	0.16464
150	2.0	4.0	2.04271	2.02747	2.01428	0.17078	0.16971	0.16916	4.00152	0.28145
	4.0	6.0	4.02171	4.00654	3.99554	0.92880	0.92837	0.92835	6.00024	0.27412

The results obtained using above programme are presented in tables 1, 2 and 3 for different values of n and mean (= 0) and hyper-parameters.It is observed that the values of the MSE of σ under both Jeffreys and Uniform prior are almost same. For the shape parameter, p , the Gamma prior provides values having less MSE as compared to Jeffreys prior. Also, it can beobserved that as the hyper-parameter values increase the MSE decreases simultaneously.

This paper deals with the approximation methods in case of the generalized normal (GN) distribution. The aim is to study the Bayes estimates of the shape and scale parameters of the generalized normal distribution. We observe that under informative as well as non- informative priors, the posterior variances under Jeffreys or Uniform prior distribution for σ are close to each other. But p has less posterior variances under Gamma prior. Thus, we conclude that we can prefer Jeffreys or Uniform prior distribution equally as a prior for the standard deviation and Gamma prior for p of GN distribution. The MSE is also seen decreasing for increasing sample size. Further, we conclude that the posterior variance based on different priors tends to decrease with the increase in sample size. It implies that the estimators obtained are consistent.