Базовые выражения, используемые в электрокинетике (обзор)

Электрокинетические процессы, являющиеся одним из подразделов электрохимии, в силу непростых математических моделей, описывающих нелинейные связанные взаимодействия нескольких физических полей, описывающих поведение процесса, стали с появлением развитых вычислительных пакетов объектом пристального внимания. Без использования таких пакетов решение сколько-нибудь сложных по геометрии или по количеству связанных полей задач представляется весьма проблематичным. В настоящем обзоре приводятся основные математические модели, которые могут быть востребованы при моделировании электрокинетических процессов при их физическом усложнении, например при учете влияния изменения температуры на параметры процесса (вязкость, коэффициент диффузии, конвективные процессы и т. д.), учете градиента давления и т. д. С этой целью приводится обзор некоторых математических моделей, описывающих различные аспекты процесса.

ЭЛЕКТРОСТАТИКА

Приведем некоторые базовые выражения, касающиеся электростатики и закона сохранения зарядов. Основной задачей электростатики является отыскание векторов напряженности электрического поля E и электрической индукции (электрического смещения) D в каждой точке электрического поля, созданного данной системой источников поля — электрических зарядов [1, с. 248].

Уравнения электростатики являются частным случаем полной системы уравнений Максвелла для электромагнитного поля [1, с. 501], когда его характеристики — электрическая индукция (электрическое смещение) D и напряженность электрического поля E — не зависят от времени. Содержательные уравнения в системе уравнений Максвелла имеют в этом случае вид [1]:

V. D = V- ( 88 o E ) = P el   ( в СИ ) ,

V- D = V- ( 8 E ) = 4np_el ( в СГСЭ ) ;

Vx E = 0 ( в СИ и СГСЭ ) .            (2)

Исходя из (2), поле E является потенциальным

E =-V ^ .

Здесь 80 = 8.85-10—12 Кл2/(Н- м2) = 8.85-10—12 Ф/м — электрическая постоянная; ε — относительная диэлектрическая проницаемость среды, показывающая во сколько раз сила взаимодействия между двумя постоянными зарядами в данной среде меньше чем в вакууме; ϕ — скалярный потенци- dq ал; pd =--объемная плотность заряда; dq — el dV величина заряда, сосредоточенного в объеме dV. Для вектора D справедливо представление

D= εε ₀ E (в СИ);   D= ε E (в СГСЭ).

Нормальная составляющая вектора D к границе раздела двух диэлектриков (при отсутствии заряда на границе) непрерывна (не претерпевает разрывов) в отличие от нормальной составляющей вектора E . Это следует из (1) при p el = 0 на границе.

Выражение (1) является формулировкой теоремы Остроградского—Гаусса в дифференциальной форме.

При заданном распределении свободных зарядов потенциал ϕ электростатического поля в однородном и изотропном диэлектрике в ε раз меньше чем потенциал ϕ ₀ в вакууме и удовлетворяет уравнению Пуассона, что следует из (1) и (3) А_ф = - ^p (в СИ),    А ф = - ^{4 пР}- (в СГСЭ). (4)

εε 0                      ε

Приведем также дифференциальную форму закона сохранения заряда — уравнение непрерывности для объемной плотности зарядов [1, с. 504]

V- j + ^Р = 0.             (5)

о t

Здесь j — плотность токов проводимости.

Отметим, что в иностранной литературе, например в [2], применяются несколько отличные обозначения: через ε обозначается не относительная диэлектрическая проницаемость среды, как в отечественной литературе, а совокупная диэлектрическая проницаемость среды, равная произведению электрической постоянной ε ₀ на относительную диэлектрическую проницаемость среды, обозначаемую в этом случае через ε_r .

УРАВНЕНИЕ НАВЬЕ—СТОКСА ПРИ ВОЗДЕЙСТВИИ ВНЕШНЕГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ

Закон сохранения импульса при движении вязкой несжимаемой жидкости, к которой приложено внешнее электрическое поле с напряженностью E , в дифференциальной форме записывается в виде уравнения Навье—Стокса (см., например, работу [2, с. 141])

dv p— + (v -V)v = -Vp + pAv + pg + pZE . (6) d/                                      e

Здесь v , p — поля вектора скорости и давления в жидкости; ρ — ее плотность, η — вязкость; g — вектор ускорения силы тяжести; ρ_el — по-прежнему объемная плотность электрического заряда.

ЭЛЕКТРОХИМИЧЕСКИЙ ПОТЕНЦИАЛ

Движущей силой диффузии служит пространственная вариация химического потенциала данного вещества. В отсутствие электрического поля химический потенциал µ растворенного вещества для условий, при которых вкладом гидростатического давления можно пренебречь, равен [5, с. 79]

c p = p0 + RT In—, c0

где µ ₀ — стандартный химический потенциал, зависящий от природы растворителя при постоянной концентрации примеси частиц c ₀ и отсутствии электрического поля; c — реальное поле концентрации частиц (понятие концентрации ниже уточняется в силу ее неоднозначного определения). Для ионов, движение которых зависит не только от концентрации, но и от электрического потенциала, соответствующим понятием является электрохимический потенциал µ [5, с. 79]:

p = p ₀ + RT In ^— + ZFф .

c ₀

Электрохимический потенциал — мера работы, необходимой для переноса 1 моля ионов из раствора с данной концентрацией и данным электрическим потенциалом в бесконечно удаленную точку в вакууме. Эта работа складывается из затрат на преодоление сил химического взаимодействия p ₀ + RT In c и работы по переносу зарядов в электрическом поле ZFϕ [5, с. 80].

Иногда работу по переносу ионов относят не к молю, а к одному иону [5, с. 80]

c p = p0 + kBT ln— + Zeф .

c ₀

Здесь учтено, что k B = R / N A и e = F / N A . Введены обозначения: N A ~ 6.022141 - 10 23 моль^-1 — число Авогадро; F — число Фарадея, F = eN A « ~ 96485.33Кл - моль ^{- 1}; Z — заряд иона в единицах заряда протона (безразмерная величина, равная валентности иона с учетом знака его избыточного за-

Дж ряда); R « 8.31446 ------- — универсальная газо- моль- К вая постоянная; kB = 1.3806488 -10-23 Дж/Кл — постоянная Больцмана; T — абсолютная температура в К; e = 1.602176565-10-19 Кл — элементарный электрический заряд (заряд протона).

Пассивное движение ионов (примесей) происходит из области с высоким электрохимическим (химическим) потенциалом в область с низким электрохимическим (химическим) потенциалом. Движущей силой является градиент электрохимического (химического) потенциала.

В работе [2, с. 146] дано определение электрохимического потенциала отдельно для концентраций положительно и отрицательно заряженных ионов (о чем будет говорить соответствующий спаренный знак ±)

c ( r )

Ц ± ( r ) = ^ 0 + к в Т ln — ± Zeф( r ) .     (7)

c ₀

ясно, что потенциал будет зависеть только от нормальной к этой плоскости координаты (например z ) и в этом случае он равен [2, с. 147]

Знак "  + " соответствует положительным, а знак "  - " — отрицательным ионам. Ионы в примеси здесь полагаются обратно заряженными Z₊ = Z = Z . +     —

В условиях термодинамического равновесия электрохимический потенциал постоянен: Д . ( r ) = const [2, с. 146]. Исходя из этого, после воздействия на обе части равенства (7) оператором V получается равенство

ф ⁽ z ) =

4 k T

^B Arth

Ze

th

Z- 1

V 4 к в Т J

exp

—

V

λ D

При получении (11) использовались краевые условия c ± ( да ) = c ₀, ф ( да ) = 0, ф (surf) = l , где ϕ (surf) — потенциал на поверхности стенки; ς — дзета-потенциал (см., например, [4, 5, 7]).

В (11)

к в V

T ln V

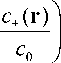
= + Ze V ф( г ),

ss ₀ k_BT = / ss ₀ RT 2 ( Ze )² c ₀ " V 2 Z ² F ² С о

которое при малых градиентах температуры V Т сводится к более простому равенству

1 c(r)   + Ze ( X ln -— = w^(r), c0    kBT

т. н. дебаевская длина, или радиус экранирования ^c

[5, т. 2, с. 88]. Здесь С о = —— — концентрация NA в моль м3 (см. ниже). Как видно, длина экраниро-

откуда получается равенство (статистическое уравнение Больцмана), связывающее концентрацию ионов с электрическим потенциалом

c ± ( r ) = c 0 exp

Г + Ze (         Г + ZF

— ^ ^{( r )} I = ^c o ^ex P I k T            RT

B

ϕ ( r )

вания существенно зависит от концентрации ионов: в разбавленных водных растворах длина экранирования (т. е. область диффузного двойного слоя) достигает десятков нанометров, а в концентрированных растворах — десятых долей нанометров [там же, с. 89].

В случае выполнения приближения Дебая (или модели Гуи), когда тепловая энергия превосходит электрическую энергию [2, с. 147]

ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ

Электрический потенциал получают из уравнения (4). Сошлемся на работу [2]. Для вычисления величины объемной плотности заряда справа в (4) используется выражение [2, с. 147]

P el = ^Ze ( ^C + ^{( r ) — C} — ^{( r )} ) .                ⁽⁹⁾

Здесь c ₊ ( r ) ( c _— ( r )) — концентрация, подразумевающая число положительно (отрицательно) заряженных ионов в единице объема в точке r .

Концентрация c ± ( r ) находится из выражения (8).

После подстановки (8) и (9) в уравнение Пуассона (4) получено следующее нелинейное уравнение для электрического потенциала (уравнение Пуассона—Больцмана) (см. [2, с. 147]):

Z_ec    Г Ze

^А ф ( r ) = 2----sh — ^ ( r ) I .       ⁽¹⁰⁾

ss о    V k B T      J

Уравнение (10) в общем случае необходимо решать численно, однако в ряде случаев существует аналитическое решение. Один из них — это случай однородно заряженной плоскости. Тогда

Zeq « k_BT ,               (13)

получают линеаризованное приближение уравнения (10) в виде уравнения Дебая—Хюккеля

^А ф ( ^r ) = ТГ ф ( ^г ) .            ⁽¹⁴⁾

λD

Например, в случае зависимости только от координаты z при z >  0 и граничном условии ф _z=_o = l (точное решение уравнения (10) имеет вид (11)) решение (14) таково [2, с. 148]:

ф ( ^z ) = L ^ex P

z λ D

В случае цилиндрического капилляра радиусом a уравнение (14) преобразуется к виду

Г d 2,1 d 1

— + -— Iф(r) = —ф(r), Vd r r о r J r e[0, a ],       (16)

ф(a) = L .(17)

^{5 2}ф

Член в уравнении (16) равен нулю вслед- д z¹

ствие предположения о цилиндрической симметрии задачи. Решением этой краевой задачи является [2, с. 149]

, o                                 дp

[8, с. 81], v — v e , и Vp ——, и, в силу осевой z z             дz симметрии, vz — vz (r). Тогда стационарное уравнение (6) без учета силы тяжести записывается в виде

ф ( r ) = S

1 0 ( r / X d )

I о ( a / X d ) ^.

^- | p ⁺ П ^{А V} _z ⁺ P el ^E z = ^0. д z

Здесь I ₀ — модифицированная функция Бесселя нулевого порядка.

Отметим, что по известному распределению потенциала можно легко найти распределение плотности электрического заряда из уравнения (4), а именно

Далее вывод приводится подробно вследствие допущенных в [7] неточностей. После выделения из последнего уравнения плотности заряда

д p

P ei ^{— — ss} о ^А Ф .               ⁽¹⁹⁾

P el =

д z

- П

Г д ²    1 д )

+       I V z

V д r   r д r )

E z

Для потенциалов (15) и (18) справедливы соответственно выражения [2, с. 148, 149]

д ф    ssosz

Pel = —ss о АФ = —ss о —T = —, 2 exp —— I,(20)

^{д z      X} d    V ^X d )

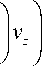
и подстановки его в уравнение (4) получается уравнение

( д2   1 д)        1 Гдp    ( д21

2 +I ф —П2"

_V д r ² r д r )       ss ₀ E_z V д z    V д r ² r д r

= - ss o S I 0 ^{( r} / ^X d ) l       X D I о ( a / X d ) .

решением которого является следующее поле скоростей:

Использование приближения Дебая (13), (14) позволяет в ряде случаев легко найти из (8) выражения для концентраций c ± ( r ). Для плоскости это выражение выглядит так [2, с. 148] (здесь внешняя экспонента заменяется первыми двумя членами ряда):

z X ss / I \ д pa ² — rr v_z ^{( r} ) ^— E z — ( ф ^{— ф} _г._a)^— -------

П \ ^r a) д z 4n

.

c ± ⁽ z ) = c о exp

Ze

.⁺ k B T ^{Ф z} )

c ₀

¹ + fe| exp (^{— z} / ^X d ) . ^k B ^T                _

При интегрировании выражения (24) были приняты следующие краевые условия: v_z — 0 при r — a , v_z и ф при r — 0 конечны.

В работе [2, с. 163] выражение (24) представлено в законченном виде путем подстановки в него выражения для потенциала (18), полученного

ТТ                         I \     ¹ 0 ^{( r} / ^X D )

из уравнения Дебая—Хюккеля, ф ( r ) — s —т-----г :

I о ( a / X d )

Для цилиндрического капилляра использование (18) и замена экспоненты первыми двумя членами разложения дает следующее выражение:

v z ( ^r )^— E z ^{SS 1} S ^η

Г I о ( r / X d ) _ )

V I о ( a / X d )    )

—

д p a ²

—

д z  4n

^r . (25)

c ± ( r ) = c 0 exp

c ₀

Ze

⁺ k B T ^{Ф ( г )}

Zes I о ^{( r} / ^X d )

1 +--"-------- квТ1о (a / Xd )

Из выражения (24) видно, что при отсутствии внешнего электрического поля ( E_z — 0), поле скоростей совпадает с течением Пуазейля в круглой трубке

/ _x    д pa ² — r ²

vz (r) — ——------, zV ’    дz   4n

В работах [2, с. 162] и [7, с. 220] решается уравнение баланса импульса, следующее из уравнения Навье—Стокса для стационарного течения в цилиндрической трубке с осью вдоль оси Oz при предположении E — Ezez. Тогда, как известно дp n а при равенстве градиента давления нулю — — 0 дz течение определяется как осмотическое, если учесть, что фг—а — S , vz (r) — Ez П (Ф — S ) .

Замечание. По оценкам [2, с. 159] на практике при наличии электроосмоса имеет место следующий порядок величин:

• - ^ -потенциал обычно с, = 100 мВ;

• – скорость течения в процессе электроосмоса v_eo = 1 мм/с;

  – подвижность для различных ионов представлена в достаточно обширной справочной литературе.

УРАВНЕНИЕ ДИФФУЗИИ ДЛЯ РАСТВОРОВ С УЧЕТОМ КОНВЕКЦИИ

Пусть в растворе присутствует n примесей, включая растворитель. Тогда масса α -й примеси в единице объема будет равна ее парциальной плотности ρ _α . Таким образом, плотность раствора, очевидно, равна

n

Р = L Р а .               ⁽²⁶⁾

а = 1

Уравнение неразрывности для раствора в целом остается таким же, как и для однородной (гомогенной) среды [2, 6 и др.]

«Р + V 5 t

выраженное в терминах безразмерного коэффициента концентрации C _α (см., например, [2, с. 94]):

ас

+ v -V С„ = D А С„ .

α αα д t

Для слабых растворов (т. е. при умеренных концентрациях примесей, когда и справедливо уравнение Фика (29)) эквивалентная плотность смеси ρ приблизительно равна плотности растворителя р* . Уравнение сохранения (30) может быть

N переписано в терминах концентраций с _а = —^ , где N _α — число молекул примеси α в объеме V . Из короткой цепочки равенств видно

Na Р Nama  Р f ca =    ==Са ,

V  ma р V  та т. е. концентрации cα и Cα — линейно зависимые функции. Здесь mα — масса одной молекулы примеси α. Отсюда уравнение (30) сразу переписывается в терминах концентраций cα [2, с. 94]

( Р v ) = 0.

-+ + v -V c_a = Da А c_a .      (31)

α αα д t

Безразмерная концентрация C _α определяется так [2, с. 94]

ρ _α

^С а = Р

Плотность потока массы примеси α, очевидно, равна сумме конвекционной плотности потока массы Jαconv и диффузионной плотности потока массы Jαdiff j «= j f+j .(27)

Плотность потока массы за счет конвекции равна

Jа™' = СаРv .(28)

Диффузионная плотность потока массы при умеренных концентрациях примеси определяется уравнением Фика [2, с. 94]

J=-DapVCa .(29)

Здесь D _a , [ D _a ] = м²/с — парциальный коэффициент диффузии примеси α .

Используя (27)–(29), легко получить уравнение неразрывности (или непрерывности, или сохранения массы) для α -й примеси в дифференциальной форме,

Отметим, что в неподвижной жидкости, когда v = 0, конвективный перенос примесей отсутствует и уравнения (30) и (31) переходят к классическим уравнениям диффузии.

УРАВНЕНИЕ ЭЛЕКТРОДИФФУЗИИ

Источником диффузии является наличие ненулевого градиента химического потенциала [5, с. 79]. Для ионов, движение которых зависит не только от концентрации, но и от электрического потенциала, дополнительно к диффузии возникает миграция ионов под воздействием электрического поля. В этом случае источником движения частиц является наличие ненулевого градиента электрохимического потенциала [5, с. 79–80]. При наличии диффузии, конвекции и миграции плотность потока массы (22) должна учесть и составляющую плотности потока миграции заряженных частиц α -компонента раствора:

J

α

diff

+ J

conv

α

+ j migr .

В работе [7, с. 245] представлена суммарная плотность потока массы J α (уравнение Нернста—Планка)

J а = - X _a U _a FC a V_V - D _a V С а + С а v ..     (32)

моль

Здесь J а , I J a I = —2—; v — вектор скорости сме-L J   м2с моль си в целом; Cα ,      , — соответствующая кон- м3

центрация α -компоненты; D _α — коэффициент диф-

,       ,         , r п моль•c м2•моль фузии (см выше); Ua , [Ua]--= —------, — кг Дж • с подвижность ионов; zα — заряд иона вида α в единицах заряда протона (безразмерная величина, равная валентности иона с учетом знака его избыточного заряда).

Результирующий ток в растворе электролита равен [7, с. 246]

I = F £ Z a J а .            (33)

α

Условие сохранения массы имеет вид [7, с. 246]

S Са д t

~

-V • J а + R _a

- Z _a U _a FC a V ф - D _a V С а + С а V ) + R a .   (34)

Здесь R α — источник, обусловленный гомогенной химической реакцией.

Наконец практически во всем объеме, занятом раствором, кроме тонкого двойного электрического слоя, принимается условие его электрической нейтральности [7, с. 247]

У Z a C a = 0.              (35)

α

Приведем физический смысл уравнений (32)–(35) [7, с. 247]. Эти четыре уравнения дают замкнутое описание процессов переноса в растворах электролитов: согласно уравнению (32) компоненты в растворе могут двигаться за счет миграции (первое слагаемое справа), диффузии (второй член) и конвекции (третий член). Уравнение (33) просто отражает тот факт, что электрический ток обусловлен движением заряженных компонентов. Уравнение (34) дает условие материального баланса, а уравнение (35) — условие электронейтральности.

Замечание 1. Отметим, что уравнение потока (32) не выполняется для концентрированных растворов [7, с. 248].

Замечание 2. В области правомерности уравнения потока (32) оказывается, что подвижности и коэффициенты диффузии ионов связаны. Эта связь осуществляется уравнением Нернста— Эйнштейна [7, с. 258]

D a = RTU a , (36)

которое строго применимо при бесконечном разбавлении.

Покажем связь соотношений (32) и (36) с распределением Больцмана (8) [7, с. 215].

Поток каждого из растворенных компонентов описывается уравнением Нернста—Планка (32). В случае равновесного состояния ( v = 0, J а = 0) имеем

- 2 _а и _а РС а V ф - D _a V С а = 0.

После подстановки в последнее уравнение значения D _α из (36) получается уравнение

V С.

C α

- z ^ F V ф , RT

откуда и следует распределение Больцмана (8).

Замечание 3. Покажем, что концентрация, оп-

N ределенная выше са = —^, где Na — число моле- кул примеси α в объеме V , и концентрация Cα , фигурирующая в выражениях, начиная с уравнения (32), равны между собой с точностью до постоянного множителя. Сначала отметим, что на- личие Nα частиц в объеме V равносильно нали- чию в этом объеме Nα / NA молей. По определению,

C α

число молей N _α c _α == .

V      NAV NA

Поэтому уравнение сохранения массы справедливо для обеих концентраций при условии, что моль источник Rα ,    3   , м3 • с в (34) заменяется на

число частиц r = NдRa ,------;-------, а именно

αA              3

м • с

—^а = -V • ( - z u_aFc Vф - D _a V с _а + с _аv) + r_a . (34а) αα α      α α α α

ЭЛЕКТРОЛИТИЧЕСКАЯ ДИССОЦИАЦИЯ

Электролитической диссоциацией называют распад молекул растворенного вещества на положительно и отрицательно заряженные ионы в результате взаимодействия с растворителем. Это явление обусловлено совместным действием двух причин [1, с. 386, 387] (далее в этом пункте все выражения взяты из этого источника): теплового движения и взаимодействия полярных молекул растворенного вещества, состоящих из взаимосвязанных ионов, с полярными молекулами раствори- теля (например, воды). Указанное взаимодействие приводит к ослаблению связи между ионами и облегчает разрыв этой связи при столкновении молекулы растворенного вещества с достаточно быстро движущейся молекулой растворителя или растворенного вещества. Коэффициентом диссоциации α называется отношение числа молекул n0' , диссоциировавших на ионы, к общему числу n0 молекул растворенного вещества

' n a = — n0

.

Вследствие хаотического теплового движения ионов в растворе происходит процесс воссоединения ионов противоположных знаков в нейтральные молекулы, называемый молизацией.

В условиях динамического равновесия между процессами диссоциации и молизации α удовлетворяет уравнению

1 - a

—2— = const • n ₀.

α ²

Если n ₀ ^ 0, то a ^ 1, т. е. в слабых растворах a ~ 1 и почти все молекулы диссоциированы. С увеличением концентрации раствора α убывает. В сильно концентрированных растворах

α

const n0

Отметим, что вода также диссоциирует. Константа диссоциации воды при температуре +25 °С равна 1.86 10–16. Диссоциация воды — процесс эндотермический (т. е. поглощающий тепло), поэтому с повышением температуры, в соответствии с принципом Ле-Шателье, диссоциация усиливается.

ЗАКОН ОМА ДЛЯ ТОКА В ЖИДКОСТЯХ

Плотность тока в жидкостях равна сумме плотностей токов положительных и отрицательных ионов j = j- + j+ .

Зависимость плотности тока j в жидкостях от напряженности E электрического поля, приложенного к электродам, имеет вид [1, с. 388]

F j = —Z+ n0+(u ++ u-)E ,          (37)

NA где Z+ — валентность положительных ионов в растворе; n0+ — число положительных ионов в единице объема электролита; и + и и- — подвижности соответственно положительного и отрицательного ионов, т. е. средние скорости движения этих ионов под воздействием электрического поля, напряженность которого равна единице.

Основные выражения таковы:

– закон Ома j = a E,(38)

где σ — удельная проводимость среды;

– закон Гаусса

¥•(ееoE) = Pei;(39)

– уравнение непрерывности

P + ¥• j = 0,(40)

о t где ρel — удельная плотность электрического заряда.

Подставляя (38) и (39) в (40), легко получаем уравнение dPe + _^_ 5t ее 0

ρel

= 0,

решение которого имеет вид

P el = P 0 exP I ^- Ч ,          ⁽⁴¹⁾

V T J

εε где t = —0 — время релаксации заряда.

Для хороших проводников T ~ O (10 ^{- 19}) с, для хороших изоляторов T ~ O (10³) с.

В зависимости от соотношения величин τ и t различают область, в которой необходимо изучать процесс.

При т >>  t (изоляторы) имеем приближение электростатики, при т <<  t (проводники) и т ~ t имеем приближение электрического тока: стационарного ( т <<  t ), либо переменного ( т ~ t ).

ЭЛЕКТРОФОРЕЗ

Электрофорез основан на том факте, что при контакте частиц с жидкостью в окрестностях последних образуется т. н. двойной электрический слой [4]. Поверхность частицы приобретает слой заряда определенного знака. Непосредственно с ним контактирует противоположно заряженный слой противоионов жидкости, остающийся привязанным к частице. Далее следует т. н. диффузный слой противоионов, которые могут находиться в тепловом движении. Слой ионов на частице и неподвижные и диффузные противоионы и образуют имеющий нейтральный заряд двойной электрический слой. После приложения статического электрического поля напряженностью E частицы начинают двигаться в нем в направлении, определяемом знаком заряда поверхности частицы. Пусть заряд частицы Ze , где Z целое число (отрицательное или положительное), e — элементарный заряд (электрона). Тогда электрическая сила Fel , действующая на частицу, равна

F_ei = Ze E .

При движении на частицу действует сила сопротивления Стокса

^Fdrag = - ^{6 n} na u ep .

стоянии покоя в неподвижной жидкости. В [2] приведена версия уравнения этого процесса

4    3    d u

- ^Па Рр — = ^{-6 п} П^аи + ^Fext .

3        d t

Здесь рассматривается одномерное движение частицы плотностью ρ_p и радиусом a со скоростью u в поле вязких сил Стокса (первый член справа) и постоянной силы F_ext , приложенной в начальный момент времени t = 0. Решение (43) имеет вид

и =

6 πηa

1 ^- exp

V V

9 η 2 ρ_pa ²

Yl

t

Здесь u _ep — вектор скорости электрофореза, которая определяется из баланса действующих на частицу сил

F drag + ^F eZ = — ^{6 п} П^а u ep + ^Ze ^E = ^0.

Отсюда

Ze

u ep = -----E .

6 πηa

Замечание. Фигурирующий в (42) радиус a иона не принимается равным его реальной величине a ~ 0.05 нм, а вследствие процессов гидратации принимается равным а ~ 0.2 нм. Это является следствием того факта, что ионы присоединяют к себе слой молекул воды (растворителя) [2, с. 145]. В этой же работе приведена таблица значений ионной подвижности различных ионов в водных растворах.

В работе [5, т. 2, с. 80] приведено выражение для радиуса иона с учетом гидратации

В работе [2] показано, что, согласно (44), время, характеризующее стабилизацию процесса т = 2 ρ_pa ₂

= —-—, при р, примерно совпадающей с плот-9η         p ностью воды, равно т = 5 мкс. Тогда из (44) следует, что через время t ~ 2т = 10 мкс частица практически достигает стационарной скорости F , и ~ и = ^x-.

6 πηa

Отметим, что при получении этой оценки были приняты некоторые допущения. Например, выражение для силы сопротивления движению частицы F_St = 6ппа (сила Стокса) справедливо только

в стационарном режиме движения частицы с постоянной скоростью. В случае, если частица обтекается жидкостью, уравнение для скорости частицы определяется системой уравнений движения, описывающей возмущенное наличием включения несущее течение жидкости, включающей также и уравнение для скорости самого включения, которая, как правило, не совпадает с линиями тока и амплитудой скорости несущего течения [3, с. 28–30].

r =

k B T _. 6 πDη

Здесь k B — постоянная Больцмана ( k_B ® ~ 1.38 - 10 ^{- 23} Дж • К^-1); T — абсолютная температура (К); D , м² ·с^–1, — коэффициент диффузии; П , Па • с, — динамическая вязкость растворителя.

СКОРОСТЬ ПЕРЕХОДНОГО ПРОЦЕССА ПРИ РАБОТЕ С МИКРОЧАСТИЦАМИ

Коснемся теперь скорости переходного процесса при работе с микрочастицами. В работе [2] рассматривается ускоренное движение сферической частицы, находящейся в начальный момент в со-

СВЯЗАННЫЕ СИСТЕМЫ УРАВНЕНИЙ ДЛЯ ПОЛНОГО РЕШЕНИЯ ЗАДАЧИ

Таким образом, для полного решения задачи расчета всех полей, фигурирующих в электрокине-тическом процессе, необходимо решить ряд связанных систем дифференциальных уравнений (общим количеством по числу примесей). В каждую систему должны входить следующие уравнения:

– уравнение Навье—Стокса (6);

–уравнение материального баланса — (30) (случай без электродиффузии) и (34) (при ее наличии);

– уравнение Пуассона (4);

– в случае наличия переменного теплового поля

сюда еще необходимо добавить уравнение тепло-переноса, которое при малых возмущениях может быть записано в линеаризованном виде (см., например, [9])

± ⁵ T' = _A T •+ a o T o W X o d t            K o d t "

Здесь абсолютная температура процесса равна T = T ' + T_o, где T_o — равновесная температура, а T ' — ее возмущение, при этом полагается T '« T 0 ; x ₀ — коэффициент температуропроводности жидкости; κ ₀ — коэффициент теплопроводности жидкости; p ' — избыточное давление;

„   1 Г ⁵ V )

a₀ =—^-^J — термодинамический коэффициент расширяемости при постоянном давлении.

Совместное решение этих систем позволяет рассчитать все фигурирующие здесь поля, в том числе поле концентрации каждой примеси с учетом диффузии, конвекции, миграции теплоперено-са и параметров проточного течения.

ВЫВОДЫ

В работе дан обзор основных выражений, позволяющих математически моделировать сложные задачи электрохимии вообще и электрокинетиче-ские задачи в частности в условиях связанности различных взаимодействующих в них полей.