Bearing fault detection using logarithmic wavelet packet transform and support vector machine

Автор: Om Prakash Yadav, G. L. Pahuja

Журнал: International Journal of Image, Graphics and Signal Processing @ijigsp

Статья в выпуске: 5 vol.11, 2019 года.

Бесплатный доступ

Objective: This paper presents an automated approach that combines Fisher ranking and dimensional reduction method as kernel principal component analysis (KPCA) with support vector machine (SVM) to accurately classify the defects of rolling element bearing used in induction motor. Methodology: In this perspective, vibration signal produced by rolling element bearing was decomposed to four levels using wavelet packet decomposition (WPD) method. Thirty one Logarithmic Root Mean Square Features (LRMSF) were extracted from four level decomposed vibration signals. Initially, thirty one features were rank by Fisher score and top ten rank features were selected. For effective detection, top ten features were reduced to a new feature using dimension reduction methods as KPCA and generalized discriminant analysis (GDA). After this, the new feature applied to SVM for binary classification of bearing defects. For analysis of this thirty six standard vibration datasets taken from online available bearing data center website of Case Western Reserve University on bearing conditions like healthy (NF), inner race defect (IR) and ball bearing (BB) defects at different loads. Results: The simulated numerical results show that proposed method KPCA with SVM classifier using Gaussian Kernel achieved an accuracy (AC) of 100, Sensitivity (SE) of 100%, Specificity (SP) of 99.3% and Positive prediction value (PPV) of 99.3% for NF_IRB dataset, and an AC of 100, SE of 99.8%, SP of 100% and PPV of 100% for NF_BBB dataset.

Еще

Fisher’s ranking method, inner raceway defect, ball bearing defect, kernel principal component analysis, support vector machine, wavelet packet decomposition

Короткий адрес: https://sciup.org/15016052

IDR: 15016052 | DOI: 10.5815/ijigsp.2019.05.03

Текст научной статьи Bearing fault detection using logarithmic wavelet packet transform and support vector machine

Published Online May 2019 in MECS DOI: 10.5815/ijigsp.2019.05.03

Bearings are the main part of induction motor that keep rotor and stator at equidistance and provide frictionless revolution. Due to hazardous operating and environment conditions, induction motor may exposed to a number of faults that are categorized as stator, rotor, bearing and eccentricity related faults. These fault if not detected in time then they can cause to complete failure of system that results in terms of financial, time and quality loss of products. Almost 40-50% of overall machine faults are related to bearings [1]. Thus, bearing fault detection is prime prominence and should be monitored on priority basis. For this, need effective features extracted from vibration signal produced from bearing used in induction motor and also need efficient classifier.

Bearings are classified as sleeve and rolling element bearing. Sleeve bearings are used in large size machines whether rolling-element bearings are usually used in small and medium size machines. Rolling element bearing fault analysis has become the recent issues of many researchers due to wide applications in small size induction motors for domestic and agriculture purpose [2].

Bearing defects may be detected using temperature monitoring, oil analysis, wear debris analysis, shock pulse method, stator current monitoring and vibration analysis [3, 4]. Among these, vibration signal is most reliable and robust method to detect bearing defects [5, 6]. Due to transient nature of vibration signal, frequency domain method like FFT is not effective. For this, Time frequency methods like Short Time Fourier Transform (STFT), Wavelet Transform (WT), Spectrogram, Pseudo Wigner–Ville, Empirical Mode Decomposition (EMD) etc. may be effective due to its ability to mitigate noise effect present in signal [7, 8, 9]. Among these methods, WT is most widely used due to its liberty to select mother wavelet [10, 11]. However, it cannot effectively split the high frequency band of transient signal that contains rich information about bearing defects. Wavelet packet transform (WPT) has capability to decompose a given signal into low and high frequency bands [12, 13]. WPT and Artificial Neural Network (ANN) based fault diagnosis of combustion engine is presented by Wu [14]. Due to revolution in digital computer, machine learning methods like Fuzzy Logic, Artificial Neural Network (ANN) and Support Vector Machine (SVM) are extensively in use to predict the bearing defects using WPT features of vibration signal [14, 15, 16, 17, 18]. In Some literatures, multi-scale permutation entropy (MPE) of decomposed WPT features of vibration signal was calculated [17, 18]. The MPE value of decomposed WPT features has found to be computationally efficient and robust but it excluded the non-linearity problems of signal.

In this study, logarithmic root mean square features (LRMSF) of decomposed vibration signal have been used to detect inner race and ball bearing defects due to its capability to reduce the nonlinearity problems of signal. The performance of any classification technique depends on the selection of appropriate number of features and discriminating capability of features [19, 20, 21]. For this, Fisher’s ranking method[22] was employed to select top ten features out of thirty one WPT features extracted from vibration signal. In further study, top ten features were reduced to a new feature using dimensional reduction technique as kernel principal component analysis (KPCA) [23, 24, 25]. The new feature was classified using SVM technique with Gaussian kernel function to predict the bearing defects in early stage.

The performance of proposed method was evaluated using confusion matrix parameters like accuracy (AC), sensitivity (SE), specificity (SP) and positive prediction value (PPV) for training and testing datasets. The flowchart of proposed algorithm is shown by fig.1.

Vibration data Sets	Vibration data	Features extraction		Features rank by Fisher’s	Top ten rank features	SVM Classifier
Vibration data Sets	Vibration data	Features extraction		Features rank by Fisher’s	Top ten rank features	SVM Classifier	Faulty
collected	segmented	from		Score	reduced to a	with	1____
from faulty and healthy bearing of	into equal size of 20 samples	segmented data by WPT	1		new feature using KPCA 1	Gaussian Kernel
2HP motor	into equal size of 20 samples						Healthy

Fig.1. Flowchart of the proposed methodology to detect bearing condition

II. Vibration Database

The vibration database used in this study taken from online available bearing data center website of Case Western Reserve University (CWRU)[26]. The experimental setup was consists of a 2HP Reliance made induction motor, a torque transducer/encoder, a dynamometer and control electronics circuit. Four types of single point inner raceway (IR) and ball bearing (BB) defects were seeded separately to SKF made bearing mounted to drive end (DE) of induction motor with fault diameters 0.007 inch, 0.014 inch, 0.21 inch and 0.028 inch using electro-discharge machining (EDM) technology. Thirty six data sets related to no fault (NF), IR and BB defects have been considered at machine operating loads 0HP, 1HP, 2HP and 3 HP. The vibration digital data was collected using accelerometer attached to the housing of induction motor with magnetic bases at 12000Hz sampling frequency. In this work, vibration samples were taken for 10 seconds i.e. 120000 samples of each datasets.

The vibration data sets considered to study bearing health condition are reported in Table 1. Where DS represents Dataset, NF means No Fault, IRA, IRB, IRC and IRD represent inner raceway bearing defects and

BBA, BBB, BBC and BBD symbolize ball bearing defects at fault levels respectively 0.007 inch, 0.014 inch, 0.21 inch and 0.028 inch in diameter. Fig. 2. represents the amplitude vs number of samples plot of vibration signal for bearing conditions NF, IRA, IRB and IRC at machine load 0HP.

Table1. Vibration datasets related to various bearing conditions at different operating loads of machine

Bearing status	0HP	1HP	2HP	3HP
NF	DS-I	DS-II	DS-III	DS-IV
IRA	DS-V	DS-VI	DS-VII	DS-VIII
IRB	DS-IX	DS-X	DS-XI	DS-XII
IRC	DS-XIII	DS-XIV	DS-XV	DS-XVI
IRD	DS-XVII	DS-XVIII	DS-XIX	DS-XX
BBA	DS-XXI	DS-XXII	DS-XXIII	DS-XXIV
BBB	DS-XXV	DS-XXVI	DS-XXVII	DS-XXVIII
BBC	DS-XXIX	DS-XXX	DS-XXXI	DS-XXXII
BBD	DS-XXXIII	DS-XXXIV	DS-XXXV	DS-XXXVI

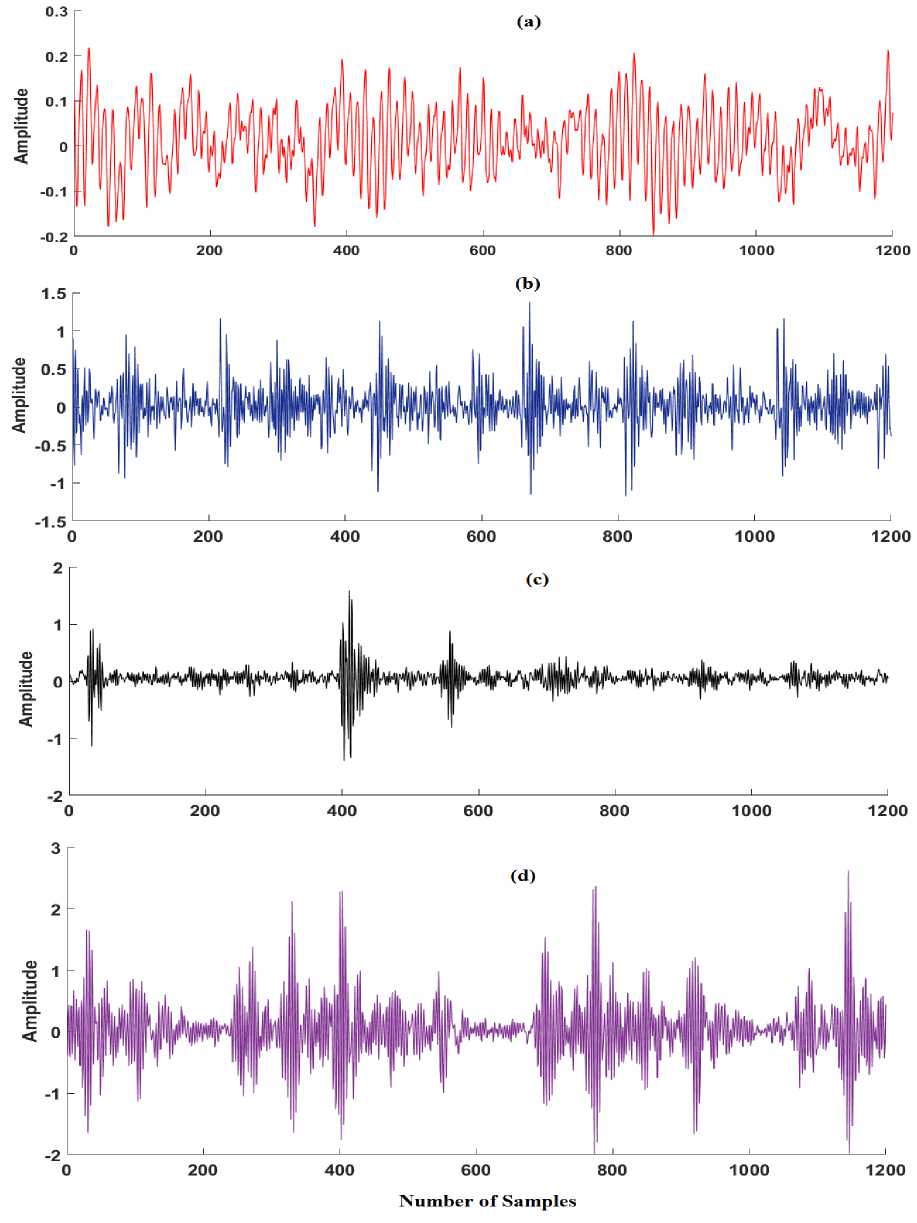
Fig.2. Representation of vibration signal for bearing conditions (a) NF (b) IRA (c) IRB (d) IRC at 0HP load

III. Fault Frequencies of Rolling Element Bearing

Rolling element bearing is most commonly used bearing that consists of four essential parts: cage (separator), inner raceway, outer raceway and rolling element (roller or ball). Lubricant contamination, lubricant loss or excess lubrication, brinelling, excess loading, overheating and corrosive environments are some basic cause to bearing failure. Bearing faults can be categorized into distributed and localized defects. Distributed defect affects the whole region of bearing and difficult to characterize by distinct frequencies, while single-point defect is confined to a small area that generate a harmonic series with fundamental frequency equal to one of four characteristic frequencies: cage defect frequency F , inner race defect F , outer race defect F and ball defect F frequencies[2]. The construction of rolling element ball bearing is shown by Fig.3. Let F is rotational frequency, Z is total no of balls, db is ball diameter, d p is pitch diameter and 5 is contact angle then the characteristic fault frequencies are represented as

Fd,

F, = F (1 - cos 5)

Frf = Zb- (1 + db cos 5) F,(2)

For, = Zb (1 — dr cos 5)Fr(3)

2 d

F, = dp- (1 - db-cos2 5) Fr db

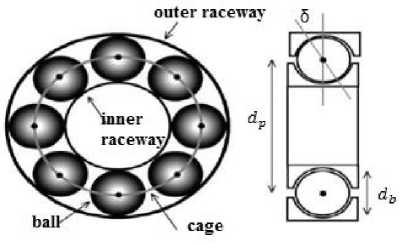
Fig.3. Internal structure of rolling element bearing

The dimensional parameters of SKF bearing are: Z_b = 09, Ball diameter d_b = 0.3126 inch, Pitch diameter d_p = 1.537 inch, so fundamental fault frequencies related to this bearing are given as

F_cf = 0.39828 x F_rF ir, = 5.4152 x F r F or, = 3.5848 x F r F_bf = 4.7135 x F_r

These frequencies are used for decomposition of vibration signal using WPT.

IV. Feature Extraction Using Wavelet Packet Transform

Wavelet Packet Transform (WPT) is the extension of wavelet transform that provides more flexible time frequency decomposition in high frequency region[13]. A wavelet packet consists of a set of linearly combined wavelet functions that are generated by the following recursive relationship

W ² k ( t ) = V2 Z s ( n )W k (2 t - n ) (5)

W ² k ⁺ ¹( t ) = V2 Z g ( n )W^k (2 t - n ) (6)

Here first two wavelet packet functions W0(t) = фt) and W 1(t) = фt) are known as scaling function and wavelet function. The symbol s(n) and g(n) are related to each other by g(n) = (—1)ns(1 — n) is coefficients of a pair of Quadrature Mirror Filters associated with the scaling function and wavelet function. WPT recursively decomposed the input discrete signal into low frequency known as Approximation and high frequency known as Details components. The input signal x(t) can be decomposed recursively as:

x j + 1,2 k ⁽ t ) = Z s ⁽ m - ² n ) x j , k ⁽ t ) ⁽⁷⁾

x j + 1,2 k + 1 ⁽ t ) = Z g ⁽ m - ² n ) x j , k ⁽ t ) ⁽⁸⁾

Where x ( t ) denotes the wavelet coefficients at the j^th level, k^th sub frequency band. Therefore the signal x ( t ) can be expressed as

2 j - 1

x ⁽ t ) = Z x j , k ⁽ t ) (9)

k = 0

Three level decomposition of the signal x ( t ) using the WPT is given in Fig.4. In this Figure solid line represents low frequency components (Approximation Coefficients) and dotted line indicates high frequency (Details Coefficients) components. The variation of amplitude with respect to time of energy content E ^k of each sub frequency band is chosen as vibration signal [13].

En i=1 x2k k (t) (10)

LRMSF = log. X² ⁺ X ² ^{+ +} X N (11)

In this work log root mean square feature (LRMSF) of decomposed signal using WPT is chosen as feature to diagnose the bearing defects[27].

Where X , X etc are samples of decomposed signal and N is number of samples in decomposed signal.

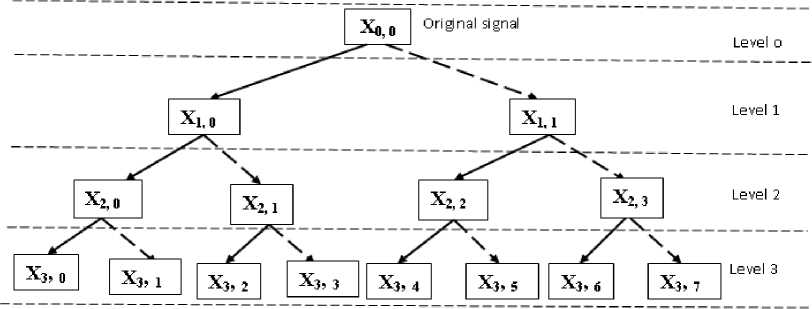
Fig.4. Three stage wavelet packet decomposition of signal x(t)

V. Feature Ranking And Dimension Reduction Methods

Features extracted from vibration signal by WPT contain significant information about the bearing defects. On the basis of information contained in the features, they can be categorized as strongly relevant, weakly relevant, irrelevant and redundant[7]. Irrelevant and redundant features reduced the efficiency and increases the processing time of fault classification algorithm. In this case, ranking method is very useful to select relevant features. For this study, we have employed Fishers ranking method to select top ten rank features on the basis of Fisher score[28]. The Fisher score is obtained by using equation (12). The Fisher score of i^th feature in j^th class matrix is define as

Zn=1 Nj(Mj —Mi)

F (i) = —------------ n

² jij

Where Д represents mean value of i t feature, Mj represents mean value of j^th feature in 1^th matrix, N represents number of samples of j^th class matrix of 1^th feature and 7 represents standard deviation.

Due to similarity in various WPT features of vibration signal which are obtained from different bearing conditions, the feature ranking method is not appropriate to select most discriminant features. In this circumstance, dimension reduction techniques like GDA and KPCA will be very constructive. The GDA is a kernel based non-linear dimension reduction technique used to transform original training or validation features space to a new high-dimensional feature space where dissimilar classes label of features are made-up to be linearly distinguishable [29]. If there is α classes label in the given features, the dimension of feature space of vibration signal can be reduced to α-1 by GDA method. In this paper, 2 numbers of classes (i.e. binary classes) are taken and the top 10 features are reduced to a new feature by GDA. The mathematical expressions of GDA are given in[30].

KPCA is the non-linear extension of principal component analysis (PCA) that map the original data sample into high dimensional space using nonlinear mapping [31, 32, 33]. In the feature space then, a linear PCA is performed estimating the eigenvectors and Eigen values of a matrix of outer products, called a scatter matrix. The mathematical expression of KPCA is given in [31]. In this work, radial basis function (RBF) and Gaussian kernels have been used to reduce the top 10 WPT features to a new feature.

VI. Support Vector Machine

SVM is a statistical learning theory based computational technique developed by Vapnik [34] for solving supervised classification and regression problem. SVM developed an optimal separating boundary with maximum margin between two classes of data. The nearest data points to boundary are known as support vectors [11][35].

Let a training set S = ( x_t , y_t )_z Lj where data points x_t e R N belong to two classes y G { — 1, + 1} . Then the hyper plane used to separate linearly separable training data into two classes can be given as[36]

H ( x ) = W T x_t + k , Where w is weighting vector and k is a scalar quantity known as bias

In such way that H ( x ) > 0 if y. = + 1 and

H ( x ) < 0 if y. =- 1

In this case the optimal hyper plane can be determined by solving following quadratic optimization problem.

min n = ^ II w 11² ⁽¹³⁾

subject to y. ( w^Tx_t + k ) > 1

If the data is linearly non-separable then it is mapped onto a higher dimensional feature space where data is linearly classified by using a transformation matrix ф(X) . In this case optimized hyper plane can be determined by solving following equation min n = 1| | w||2 + p£ Z

² i = 1

subject to y . ( w^T ф (x. ) + k ) > 1 - Z

Where p is constant and Z > 0 is known as slack variable.

After solving equation (14) the hyper plane H(x) can be expressed as

I N

H ( x ) = sign \ ^ a_iy_iK ( x i , x ) + k ^ ⁽¹⁵⁾

I i = 1 J

Where a is Lagrange multiplier, K ( x , x ) is kernel function. In this paper, Gaussian function is used as kernel function due to its performance. The Gaussian kernel [37] is given as

K ( x , x ) = exp

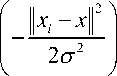
VII. Performance Index

Let N is true positive, N is false positive, N is false negative and N is true negative result then the performance parameters like Accuracy (AC), Sensitivity (SE), Specificity (SP) and positive prediction value (PPV) can be defined as

AC =----NA + ND----x ioo(17)

N_a + N_B + N_c + N_d

SE =---A— x100

N a + N_c

SP = —ND— X100

N D + N b

PPV =---A— x 100

N a + N b

VIII. Simulation Parameters

The classification performance of SVM generally depends on the selection of kernel function. In this work, Gaussian kernel based SVM is used to map the original feature samples to higher-dimensional space due to its ability to deal with nonlinearity. The generalization ability of Gaussian kernel based SVM mainly depends on three parameters C, S and ξ (epsilon)[37]. Where S represents the width of Gaussian function, C denotes the error/trade-off parameter between training error and the flatness of the solution. If value of C is high then training error will be less but training time becomes high. To overcome this problem, an optimized parameter has been obtained using 10 cross validation method. The training and validation classification performance were calculated using 10 trials-10-folds cross validation technique to ensure robustness of classifier. For each trial of the 10- fold cross-validation, the data was randomly divided into ten parts of full dataset.

IX. Simulation Results

In this work, 36 vibration data sets as given in Table 1 related to different bearing conditions ( healthy, inner race and ball bearing defect) was processed and analysed using WPD and SVM technique. Each bearing conditions are studied at machine load 0HP, 1HP, 2HP and 3HP. Initially, each data set was segmented to equal size samples of 20 segments of approximately 6000 data poits each. The result was analysed by comparing NF with IRA, IRB, IRC, IRD, BBA, BBB, BBC and BBD bearing datasets. This paper presents the comparative study of NF_IRA, NF_IRB, NF_IRC, NF_IRD, NF_BBA, NF_BBB, NF_BBC and NF_BBD data sets using WPT features in terms of mean ±standard deviation, box plot and SVM classification performance. Initially, four levels WPD have been adopted to decompose the signal into 31 sub frequency bands. In order to enhance the effectiveness and signal differentiation capability of WPD, log root mean square (LRMS) value of each sub band has been calculated. Further these 31 features were ranked to select top 10 features using Fisher’s Ranking Method. The top 10 features with their score corresponding to each data set have been shown in Table 2.

Table 2 shows the Fisher score of top 10 features extracted from considered four levels decomposed WPT features of data sets. The result of this table reflects that approximate (App.) LRMSF at fourth level decomposition of each data sets having highest score compared to third, second and first level decomposition of data sets. It indicates that four levels decomposition are appropriate for detection of bearing faults. The results also show that after App LRMSF at four levels, the App LRMSF at third level achieved high fisher score compared to App and Detailed (Det.) LRMSF at second and first level decomposition. It also observed that feature no 28 (high frequency sub band i.e. App level 4) has highest ranking.

Table 2. Fisher’s score of top 10 features of each data set arrange in descending order

Feature Level	NF_IRA	Feature	NF_IRB	Feature	NF_IRC	Feature	NF_IRD
28-LRMSF-L4-App.	1087.225	28-LRMSF-L4-App.	214.834	28-LRMSF-L4-App.	626.6247	30-LRMSF-L4-App.	1680.593
10-LRMSF-L3-App.	689.8496	10-LRMSF-L3-App.	191.4358	10-LRMSF-L3-App.	418.0746	10-LRMSF-L3-App.	1103.967
3-LRMSF-L2-Det.	654.8227	8-LRMSF-L3-App.	112.6659	20-LRMSF-L4-App.	356.2528	20-LRMSF-L4-App.	785.1135
14-LRMSF-L3-App.	648.217	7-LRMSF-L3-Det.	109.0078	3- LRMSF-L3-Det.	342.8257	16-LRMSF-L4-App.	723.6063
5-LRMSF-L2-Det.	442.8577	14-LRMSF-L3-App.	108.4772	30-LRMSF-L3-App.	333.2266	3-LRMSF-L2-Det.	594.7487
1-LRMSF-L1-Det.	314.7318	20-LRMSF-L4-App.	88.99039	5- LRMSF-L2-Det.	280.1559	5-LRMSF-L2-Det.	563.8906
12-LRMSF-L3-App.	257.535	30-LRMSF-L4-App.	83.46755	1-LRMSF-L1-Det.	237.231	30-LRMSF-L4-App.	534.1041
21-LRMSF-L4-Det.	230.5468	29-LRMSF-L4-Det.	60.95911	21-LRMSF-L4-Det.	207.2584	21-LRMSF-L4-Det.	491.0051
2-LRMSF-L1-App.	214.1689	15-LRMSF-L4-Det.	58.29484	7-LRMSF-L3-Det.	205.0714	11-LRMSF-L3-Det.	465.1864
7-LRMSF-L3-Det.	213.4095	12-LRMSF-L3-App.	57.13446	14-LRMSF-L3-App.	203.8349	12-LRMSF-L3-App.	387.4896
Feature Level	NF_BBA	Feature	NF_BBB	Feature	NF_BBC	Feature	NF_BBD
28-LRMSF-L4-App.	959.1302	28-LRMSF-L4-App.	68.74115	28-LRMSF-L4-App.	163.9424	28-LRMSF-L4-App.	2652.55
10-LRMSF-L3-App.	330.6345	10-LRMSF-L3-App.	30.52219	14-LRMSF-L3-App.	59.31873	7-LRMSF-L3-Det.	1983.119
20-LRMSF-L4-App.	267.6505	20-LRMSF-L4-App.	27.84341	20-LRMSF-L4-App.	58.11447	20-LRMSF-L4-App.	1781.732
13-LRMSF-L3-Det..	215.9525	13-LRMSF-L3-Det.	25.34067	19-LRMSF-L4-Det.	56.47606	26-LRMSF-L4-App.	1698.034
30-LRMSF-L4-App.	186.3967	14-LRMSF-L3-App.	21.35266	30-LRMSF-L4-App.	54.40991	5-LRMSF-L2-Det.	1381.877
14-LRMSF-L3-App.	127.1904	3-LRMSF-L2-Det.	19.31914	7-LRMSF-L3-Det.	46.23516	1-LRMSF-L1-Det.	1306.337
7-LRMSF-L3-Det.	122.593	11-LRMSF-L3-Det.	15.49607	10-LRMSF-L3-App.	43.88368	30-LRMSF-L4-App.	1032.959
5-LRMSF-L2-Det.	108.461	29-LRMSF-L4-Det.	15.11445	29-LRMSF-L4-Det.	34.46028	2-LRMSF-L1-App.	946.3658
21-LRMSF-L4-Det.	78.80587	5-LRMSF-L2-Det.	8.265045	21-LRMSF-L4-Det.	24.89299	21-LRMSF-L4-Det.	787.2208
29-LRMSF-L4-Det.	62.5694	24-LRMSF-L4-App.	7.455203	12-LRMSF-L3-App.	21.48748	LRMSF-L3-App.	707.4679

Fig.5. illustrate the box plot of top ten features of considered datasets in terms of minima, maxima, IQR and median value. Fig.5. (a) shows that the median value of decomposed features of NF bearing are between -2.5 to -4, while it is around -1 for IRA bearing. However in case of features LRMSF-L4-App the median value is less than -4 and feature LRMSF-L1-App. is more than -2.5 for NF bearing. Fig.5. (b) reveals the box plot of top ten decomposed features of dataset NF_IRB. The graph illustrate that median value of NF bearing for all top ten data sets are between -3 to -4 except highest scored feature LRMSF-L4-App. has its value less than -4. The plot also shows that median value of decomposed features of IRB bearing is between -1 to -2. Only in case of 7th featureLRMSF-L4-App. and 10th feature LRMSF-L3-App the median value is less than -2. Fig. 5. (c) Represents the box plot of top ten decomposed features of dataset NF_BBA. The median value of top ten features of NF bearing is less than -3 except 8th and 9th feature which value is between -2.5 to -3. The graph also indicates that the median value of all ten features of BBA bearing is more than -2. Thus the median value of top 10 features of BBA bearing is always higher than the NF bearing. Fig. 5. (d) Describe the box plot of top ten decomposed features of dataset NF_BBB. The graph shows that the median, IQR and max to min variation of decomposed features of BBB bearing is more than the NF bearing. Thus from box plot of top 10 features of all considered dataset it is concluded that the median value of NF bearing is always less than the faulty bearing. Table 3 presents the analysis of bearing defects in terms of mean value (ft) and standard deviation (SD) of top ten decomposed features. The table depicts that mean of WPD features for NF bearing is always higher than defective bearing. The table also demonstrates that mean value of top 10 WPD feature of inner race bearing defect is higher than ball bearing defect. The SD of top ten WPD features of NF bearing is lower than IR and BB bearing. From mean and SD representation of WPD features it can be concluded that mean of WPD features can play a significant role in bearing defect analysis.

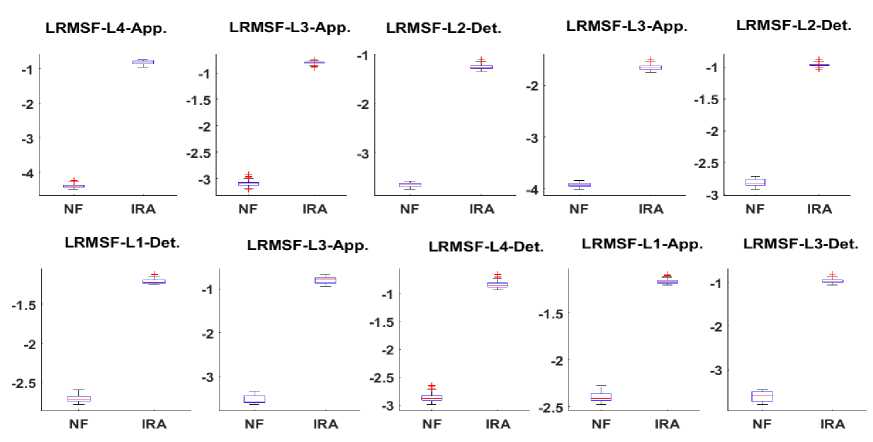
(a)

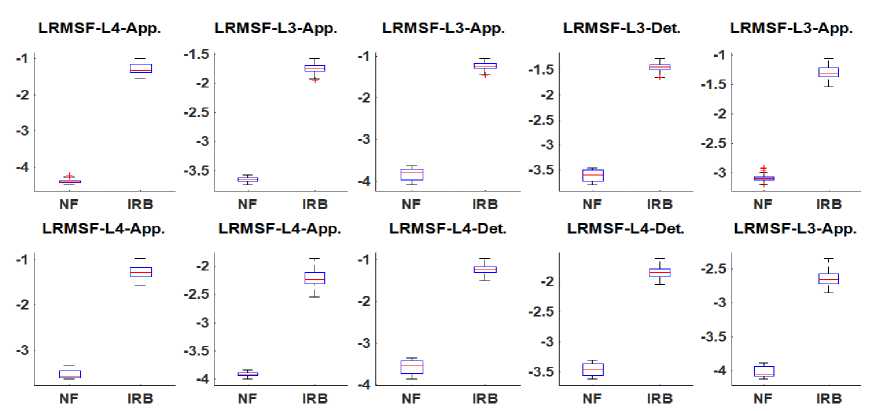
(b)

LRMSF-L4-App.

LRMSF-L3-App.

LRMSF-L3-Det.

LRMSF-L4-App.

-1	-2		-1.5	-1.5	Ф	-2.5	EjE
-2	-2.5		-2	-2		-3
-3	-3		-2.5	-2.5
				-3		-3.5
-4	-3.5	E^3	-3	-3.5		-4

В BA

LRMSF-L4-Det.

LRMSF-L4-App.

LRMSF-L3-Det.

LRMSF-L2-Det.

		^E=³	-1.5			-1.6 -1.8		Ф	-1.5
-2						-2			-2			-2
			-2.5			-2.2
-3			-3			-2.4			-2.5			-3
			-3.5			-2.6
-4			-3.5			-2.8			-3
	NF	В BA		NF	В BA		NF	В BA		NF	В BA

(c)

В BA

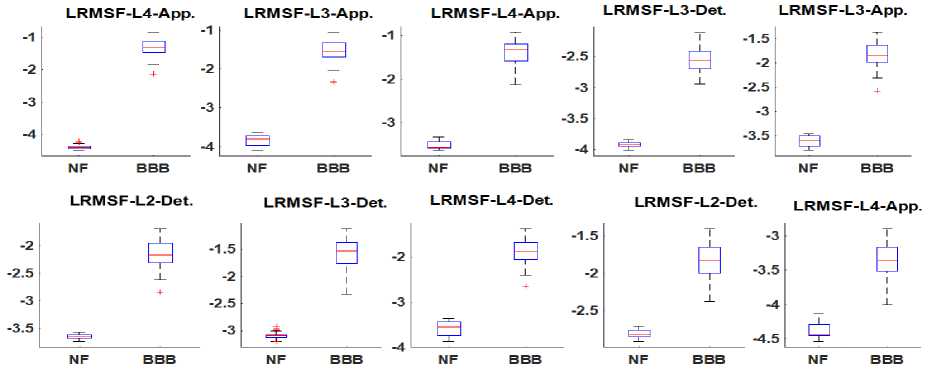
(d)

Fig.5. The box plot of top 10 features of data sets (a) NF_IRA (b) NF_IRB (c) NF_BBA (d) NF_BBB

Table 3. Mean and standard deviation representation of top 10 features of all datasets

NF		IRA		IRB		IRC		IRD
μ	±SD	μ	±SD	μ	±SD	μ	±SD	μ	±SD
-4.3935209	0.0546042	-0.8298721	0.0527802	-1.2815053	0.1388397	0.085817	0.113262	-0.75506	0.058309
-3.0929496	0.0557392	-0.8082593	0.0250827	-1.7465479	0.0852397	-0.11966	0.085637	-0.18219	0.157394
-3.6505954	0.0456595	-1.2566792	0.0472904	-1.2296049	0.0858834	0.111343	0.095796	0.00384	0.055868
-3.9155697	0.0383026	-1.6529648	0.049319	-1.4422484	0.0853146	-0.80102	0.098031	0.266525	0.108794
-2.8135806	0.0562328	-0.969671	0.0250718	-1.3018046	0.1072182	-1.44906	0.086875	-0.49001	0.078792
-2.700389	0.0503351	-1.2065993	0.0310966	-1.2776022	0.1375687	-0.42495	0.083027	0.044615	0.063174
-3.5284361	0.0958343	-0.7966947	0.071574	-2.2158098	0.1249952	-0.74931	0.073412	0.198377	0.083111
-2.868351	0.0693457	-0.8364299	0.0635091	-1.2249752	0.1213095	-0.57762	0.087705	-0.03287	0.057237
-2.3931349	0.0542599	-1.1629959	0.0233351	-1.8404476	0.1049465	-0.46586	0.098945	-0.18642	0.039455
-3.6111715	0.1184449	-0.9633122	0.046819	-2.6435599	0.1032444	-0.15302	0.102208	-1.47832	0.050379
NF		BBA		BBB		BBC		BBD
μ	±SD	μ	±SD	μ	±SD	μ	±SD	μ	±SD
-4.3935209	0.0546042	-1.21651	0.047057	-1.33085	0.253756	-1.4828	0.150115	1.58294	0.060556
-3.0929496	0.0557392	-1.92059	0.048833	-1.52732	0.252954	-1.59644	0.139275	0.716873	0.051618
-3.6505954	0.0456595	-1.42788	0.044807	-1.37449	0.270348	-1.57656	0.152265	1.385706	0.049514
-3.9155697	0.0383026	-1.30728	0.045779	-2.55267	0.186347	-2.16894	0.130797	0.120531	0.057181
-2.8135806	0.0562328	-2.31548	0.072904	-1.82001	0.24527	-2.45972	0.133292	1.076836	0.04739
-2.700389	0.0503351	-1.31902	0.046774	-2.13974	0.237182	-1.86416	0.136249	0.732469	0.043824
-3.5284361	0.0958343	-1.59586	0.048256	-1.56983	0.266105	-1.6955	0.137351	1.61373	0.058778
-2.868351	0.0693457	-1.69571	0.050265	-1.87545	0.255346	-1.76022	0.13167	0.742551	0.046753
-2.3931349	0.0542599	-1.6019	0.072389	-1.82358	0.235348	-1.86821	0.122604	0.935344	0.065312
-3.6111715	0.1184449	-1.46392	0.071396	-3.3529	0.232347	-3.15388	0.107266	-0.66104	0.046719

The classification performance of SVM with Fisher’s ranking method and dimension reduction methods like KPCA and GDA was evaluated in terms of AC, SE, SP and PPV. Each binary classification process was carried out on 160 data points in which 100 data points were used to train the classifier and remaining 60 data points were used to validate the result. The performance parameters of each datasets achieved by classifier are reported in Table 4. The results show that SVM with Gaussian kernel function achieved training parameters as AC (89.52 to 96.83), SE (86.44-94.83), SP (87.54-94.1) and PPV (88.51-95.9), while validation parameters AC (88.6-94.7), SE (80.12-92.3), SP (85.5-92.2) and PPV (86.4-94.84) for all datasets using top ten rank features. In order to improve the classification performance of SVM with Gaussian kernel function, the top 10 features were reduced to a new feature using GDA and KPCA. The SVM with GDA (having RBF kernel) attained performance parameters as AC (training (92.3-97.52), validation (92.2-96.8)), SE (training (91.52-96.9), validation (90.6-94.6)), SP (training (94.51-98.56), validation (93.4-95.82)) and PPV (training (91.34-98.32), validation (90.2-96.8)), while SVM with GDA (having Gaussian kernel) provides performance parameters as AC (training (96.34-100), validation (94.7-99.7)), SE

(training (89.5-100), validation (86.6-97.2)), SP (training (97.4-100), validation (89.6-96.8)) and PPV (training (95.1-100), validation (95.22-99.5)). The results of Table 4 reveal that the performance of SVM with KPCA (having RBF kernel) achieved as AC (training (96.76100), validation (96.3-99.7)), SE (training (94.5-100), validation (95.2-98.7)), SP (training (98.34-100), validation (97-100)) and PPV

Table 4. Comparative performance analysis of SVM technique along with feature reduction and dimension reduction methods in bearing fault analysis

Data Set (training size, validation	SVM with Gaussian
Data Set (training size, validation	Training Performance				Validation Performance
	AC	SE	1 SP 1	PPV	AC	1 SE 1	SP	PPV
NF_IRA (100x10, 60x10)	95.33	86.44	93.61	88.51	94.7	80.12	86.9	86.4
NF_IRB (100x10, 60x10)	94.23	88.91	87.54	92.14	94.22	86.61	85.5	90.41
NF_IRC (100x10, 60x10)	96.83	91.91	92.01	89.8	93.52	90.9	88.7	88.41
NF_IRD (100x10, 60x10)	90.3	92.64	93.52	94.1	88.9	91.33	90.92	89.6
NF_BBA (100x10, 60x10)	92.84	94.83	94.1	94.6	89.32	92.14	92.2	937.3
NF_BBB (100x10, 60x10)	94.62	93.42	93.13	93.3	94.4	91.63	92.14	92.9
NF_BBC (100x10, 60x10)	95.5	93.84	89.72	95.9	93.8	92.3	88.83	94.84
NF_BBD (100x10, 60x10)	89.52	92.80	92.72	93.24	88.6	91.43	90.14	92.8
Data Set (training size, validation	(GDA with RBF)+(SVM with Gaussian)
Data Set (training size, validation	Training Performance				Validation Performance
	AC	SE	1 SP 1	PPV	AC	1 SE 1	SP	PPV
NF_IRA (100x1, 60x1)	94.3	91.52	94.51	91.34	93.66	90.6	93.6	90.2
NF_IRB (100x1, 60x1)	96.5	94.21	95.32	93.15	95.5	94.2	94.5	92.5
NF_IRC (100x1, 60x1)	95.6	93.23	95.3	94.54	94.6	90.9	94.62	93.9
NF_IRD (100x1, 60x1)	97.3	93.34	94.55	96.44	96.8	92.54	93.53	95.5
NF_BBA (100x1, 60x1)	96.81	96.9	98.56	98.32	95.34	94.5	95.82	96.54
NF_BBB (100x1, 60x1)	92.3	94.32	94.62	97.75	92.2	93.6	93.4	96.8
NF_BBC (100x1, 60x1)	97.52	91.74	95.43	94.24	96.8	91.5	94.2	93.4
NF_BBD (100x1, 60x1)	96.34	95.34	95.9	97.66	94.34	94.6	93.4	96.7
Data Set (training size, validation			(GDA with Gaussian)		+ (SVM with Gaussian)
Data Set (training size, validation	Training Performance				Validation Performance
	AC	SE	1 SP 1	PPV	AC	1 SE 1	SP	PPV
NF_IRA (100x1, 60x1)	100	100	97.4	100	99.7	92.4	96.7	99.5
NF_IRB (100x1, 60x1)	98.9	89.5	100	95.9	96.4	86.6	93.52	95.5
NF_IRC (100x1, 60x1)	96.5	95.42	98.6	96.7	94.7	89.8	96.4	95.4
NF_IRD (100x1, 60x1)	99.3	96.44	97.5	98.8	95.5	93.6	92.82	95.6
NF_BBA (100x1, 60x1)	96.9	100	100	98.8	95.6	95.8	89.6	96.5
NF_BBB (100x1, 60x1)	100	98.6	100	96.7	99.2	92.5	95.5	95.22
NF_BBC (100x1, 60x1)	98.43	97.7	99.8	95.1	96.8	91.83	96.8	93.8
NF_BBD (100x1, 60x1)	96.34	97.51	100	98.33	96.2	97.2	94.5	97.9
Data Set (training size, validation	(KPCA with RBF)+ (SVM with Gaussian)
Data Set (training size, validation	Training Performance				Validation Performance
	AC	SE	1 SP 1	PPV	AC	1 SE 1	SP	PPV
NF_IRA (100x1, 60x1)	97.14	100	98.34	97.53	96.12	97.4	97	96.9
NF_IRB (100x1, 60x1)	100	100	99.21	100	99.5	98.5	99	99.74
NF_IRC (100x1, 60x1)	99.33	98.63	99.41	99.9	97.9	97.9	99.2	99.6
NF_IRD (100x1, 60x1)	96.72	96.5	98.54	98.84	96.3	95.2	98.5	97.32
NF_BBA (100x1, 60x1)	100	98.4	99.51	99.8	99.7	95.54	99.4	99.4
NF_BBB (100x1, 60x1)	98.5	100	100	100	97.4	97.8	100	99.90
NF_BBC (100x1, 60x1)	98.34	97.64	98.9	99.52	97.3	98.7	97.9	99.14
NF_BBD (100x1, 60x1)	99.3	100	100	99.63	97.8	100	97.4	98.9
Data Set (training size, validation	(KPCA with Gaussian) + (SVM with Gaussian)
Data Set (training size, validation	Training Performance				Validation Performance
	AC	SE	1 SP 1	PPV	AC	1 SE 1	SP	PPV
NF_IRA (100x1, 60x1)	99.73	100	99.38	98.68	99.5	100	98.5	98.5
NF_IRB (100x1, 60x1)	100	100	100	100	100	100	99.3	99.3
NF_IRC (100x1, 60x1)	99.61	99.57	100	100	99.4	98.6	100	100
NF_IRD (100x1, 60x1)	99.8	100	99.5	99.9	98.9	100	98.8	99.2
NF_BBA (100x1, 60x1)	100	100	100	100	99.6	100	99.2	99.2
NF_BBB (100x1, 60x1)	100	100	99.6	100	100	99.8	100	100
NF_BBC (100x1, 60x1)	99.84	99.32	100	99.4	99.6	98.9	100	99.82
NF_BBD (100x1, 60x1)	100	100	100	100	99.9	100	99.1	100

(training (97.53-100), validation (96.9-99.9)), while SVM with KPCA (using Gaussian kernel) attained highest performance parameters as AC (training (99.61100), validation (98.9-100)), SE (training (99.32-100), validation (98.6-100)), SP (training (99.38-100), validation (98.5-100)) and PPV (training (98.68-100), validation (98.5-100)) compared to other considered methods for all datasets.

X. Discussion About Result

In this article, the use of SVM combine with Fisher’s ranking method and KPCA have been presented first time to detect bearing defects at various loads. The simulated above results in the form of box plot and performance parameters show that our proposed method achieved highest performance parameters compared to other method. This happened due to use of SVM with Fisher’s ranking method and KPCA as dimension reduction method. KPCA reduces the dimension of top ten rank features to a new feature on the basis of Eigen matrix value. Table 5 represents the comparative study of related work done to determine the bearing defects using feature extraction methods like Continuous Wavelet Transform (CWT), Discrete Meyer Wavelet Transform, time domain features, Ensemble empirical mode decomposition (EEMD), Fourier–Bessel (FB) expansion and WPT. In these articles, various intelligent classifiers like Hidden Morkov Model (HMM), Adaptive Network based Fuzzy Inference System (ANFIS), Simplified fuzzy ARTMAP (SFAM), ANN, Linear Discriminant Analysis

(LDA) and SVM have been used. Continuous wavelet transforms (CWT) and SVM technique was used by some authors to detect bearing defect with some loss of high frequency information and 100% accuracy [9, 10]. Eristi and team detected power system disturbances using WT based time domain features and SVM method and achieve accuracy up to 99.37 [11]. Tabrizi and team presented a method using WPD, Ensemble empirical mode decomposition (EEMD) and SVM to detect rolling element bearing defect with 93.8% accuracy [15]. In recent articles, Multi scale permutation entropy (MPE) of WPT feature, time domain based methods, Fourier Bessel expansion was used to extract features for successful classification of bearing defects with classification accuracy 94.2%, 99.89%, 98.1%, 98.94% and 96.33% [16, 17, 19, 20, 24]. In [29], Fourier–Bessel (FB) expansion and simplified

Fuzzy ARTMAP (SFAM) has been used to derive bearing health condition with 100% accuracy using stator current but it suffers at high frequency of signal. Altmann has utilized discrete wavelet transform and adaptive network-based fuzzy inference system (ANFIS) method to diagnose bearing defect with 99.8% accuracy but it is applicable to only low speed electrical machines [38]. The proposed work utilizes WPT features of vibration signal along with Fisher’s ranking method and dimension reduction technique KPCA to classify bearing defects. The proposed method provides up to 100% classification accuracy. It also provides enhanced performance parameter along with fast response.

Table 5. Comparative performance analysis of related work

Reference No

Feature Extraction Method Feature Reduction method Classification Technique ^{Classification}

Accuracy (%)

[9]

Linear Discriminant

Discrete Meyer Wavelet Transform SVM 100

Ananlysis (LDA)

[10]

WT features with advanced signal

- SVM 100

processing

[11]

[15]

WT based Time domain features Sequential forward selection SVM 99.37

Ensemble empirical mode decomposition

Filter ranking method SVM 93.8

(EEMD)

[16]

[17]

[19]

MPE of WPT features Ranking Method Hidden Morkov Model (HMM) 94.2

MPE of WPT features GDA SVM 99.89

10 statistical and 3 frequency domain

PCA SVM 98.1

features

[20]

Time Domain Features ^{Laplacian and Brute Force} LDA, SVM 98.94

Method

[24]

[29]

[38]

Time Domain Features KPCA SVM 96.33

Fourier–Bessel (FB) expansion GDA Simplified fuzzy ARTMAP (SFAM) 100

Discrete Wavelet Packet Transform PCA ^{Adaptive Network based Fuzzy} 99.8

Inference System (ANFIS)

Proposed Work

_WPT Fisher’s ranking method _{SVM 100}

and KPCA

XI. Conclusion

In this manuscript, a novel approach has been proposed to detect bearing defects using vibration signal produced by induction motor. The proposed method is based on SVM along with Fisher’s ranking method and dimension reduction method KPCA. The result shows that box plot can be used to detect small variation of faulty signal in the form of median and IQR. The simulation result suggest that the excellent classification performance parameters like AC, SE, SP and PPV achieved by our proposed method can be employed to detect and asses the bearing faults at different loads.

Список литературы Bearing fault detection using logarithmic wavelet packet transform and support vector machine

S. Nandi, H. A. Toliyat, and X. Li, “Condition monitoring and fault diagnosis of electrical motors - A review,” IEEE Transactions on Energy Conversion, vol. 20, no. 4. pp. 719–729, 2005.
N. Tandon, G. S. Yadava, and K. M. Ramakrishna, “A comparison of some condition monitoring techniques for the detection of defect in induction motor ball bearings,” Mech. Syst. Signal Process., vol. 21, no. 1, pp. 244–256, 2007.
P. Zhang, Y. Du, T. G. Habetler, and B. Lu, “A survey of condition monitoring and protection methods for medium-voltage induction motors,” IEEE Transactions on Industry Applications, vol. 47, no. 1. pp. 34–46, 2011.
M. Blodt, P. Granjon, B. Raison, and G. Rostaing, “Models for bearing damage detection in induction motors using stator current monitoring,” IEEE Trans. Ind. Electron., vol. 55, no. 4, pp. 1813–1822, 2008.
F. Immovilli, A. Bellini, R. Rubini, and C. Tassoni, “Diagnosis of bearing faults in induction machines by vibration or current signals: A critical comparison,” IEEE Trans. Ind. Appl., vol. 46, no. 4, pp. 1350–1359, 2010.
C. Ruiz-Cárcel, V. H. Jaramillo, D. Mba, J. R. Ottewill, and Y. Cao, “Combination of process and vibration data for improved condition monitoring of industrial systems working under variable operating conditions,” Mech. Syst. Signal Process., 2016.
H. Qiu, J. Lee, J. Lin, and G. Yu, “Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics,” J. Sound Vib., 2006.
O. Rioul and M. Vetterli, “Wavelets and Signal Processing,” IEEE Signal Process. Mag., 1991.
S. Abbasion, A. Rafsanjani, A. Farshidianfar, and N. Irani, “Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine,” Mech. Syst. Signal Process., vol. 21, no. 7, pp. 2933–2945, 2007.
P. Konar and P. Chattopadhyay, “Bearing fault detection of induction motor using wavelet and Support Vector Machines (SVMs),” Appl. Soft Comput., vol. 11, no. 6, pp. 4203–4211, 2011.
H. Erişti, A. Uçar, and Y. Demir, “Wavelet-based feature extraction and selection for classification of power system disturbances using support vector machines,” Electr. Power Syst. Res., vol. 80, no. 7, pp. 743–752, 2010.
Y. Wang, G. Xu, L. Liang, and K. Jiang, “Detection of weak transient signals based on wavelet packet transform and manifold learning for rolling element bearing fault diagnosis,” Mech. Syst. Signal Process., 2015.
Z. Zhang, Y. Wang, and K. Wang, “Fault diagnosis and prognosis using wavelet packet decomposition, Fourier transform and artificial neural network,” J. Intell. Manuf., 2013.
J.-D. Wu and C.-H. Liu, “An expert system for fault diagnosis in internal combustion engines using wavelet packet transform and neural network,” Expert Syst. Appl., 2009.
A. Tabrizi, L. Garibaldi, A. Fasana, and S. Marchesiello, “Early damage detection of roller bearings using wavelet packet decomposition, ensemble empirical mode decomposition and support vector machine,” Meccanica, 2015.
L. Y. Zhao, L. Wang, and R. Q. Yan, “Rolling Bearing Fault Diagnosis Based on Wavelet Packet Decomposition and Multi-Scale Permutation Entropy,” Entropy, 2015.
S. De Wu, P. H. Wu, C. W. Wu, J. J. Ding, and C. C. Wang, “Bearing fault diagnosis based on multiscale permutation entropy and support vector machine,” Entropy, 2012.
Daisuke Matsuoka, “Extraction, classification and visualization of 3-dimensional clouds simulated by cloud-resolving atmospheric model,” Int. J. Model. Simulation, Sci. Comput., vol. 8, no. 4, pp. 1–15.
T. W. Rauber, F. De Assis Boldt, and F. M. Varejão, “Heterogeneous feature models and feature selection applied to bearing fault diagnosis,” IEEE Trans. Ind. Electron., vol. 62, no. 1, pp. 637–646, 2015.
B. R. Nayana and P. Geethanjali, “Analysis of Statistical Time-Domain Features Effectiveness in Identification of Bearing Faults from Vibration Signal,” IEEE Sens. J., vol. 17, no. 17, pp. 5618–5625, 2017.
J. G. Dy and C. E. Brodley, “Feature Selection for Unsupervised Learning ,” J. Mach. Learn. Res., 2004.
J. Tang, S. Alelyani, and H. Liu, “Feature Selection for Classification: A Review,” Data Classif. Algorithms Appl., 2014.
C. Rajeswari, B. Sathiyabhama, S. Devendiran, and K. Manivannan, “Bearing fault diagnosis using multiclass support vector machine with efficient feature selection methods,” Int. J. Mech. Mechatronics Eng., 2015.
C. Wang, L. M. Jia, and X. F. Li, Fault diagnosis method for the train axle box bearing based on KPCA and GA-SVM. 2014.
F. Deng, S. Yang, Y. Liu, Y. Liao, and B. Ren, “Fault Diagnosis of Rolling Bearing Using the Hermitian Wavelet Analysis, KPCA and SVM,” in Proceedings - 2017 International Conference on Sensing, Diagnostics, Prognostics, and Control, SDPC 2017, 2017.
“Case Western Reserve University Bearing Data Center.” [Online]. Available: http://csegroups.case.edu/bearingdatacenter/pages/welcome-case-western-reserve-university-bearing-data-center-website.
R. N. Khushaba, S. Kodagoda, S. Lal, and G. Dissanayake, “Driver drowsiness classification using fuzzy wavelet-packet-based feature-extraction algorithm,” IEEE Trans. Biomed. Eng., 2011.
O. Aran and L. Akarun, “A multi-class classification strategy for Fisher scores: Application to signer independent sign language recognition,” Pattern Recognit., 2010.
V. T. Tran, F. AlThobiani, A. Ball, and B. K. Choi, “An application to transient current signal based induction motor fault diagnosis of Fourier-Bessel expansion and simplified fuzzy ARTMAP,” Expert Syst. Appl., 2013.
B. M. Asl, S. K. Setarehdan, and M. Mohebbi, “Support vector machine-based arrhythmia classification using reduced features of heart rate variability signal,” Artif. Intell. Med., 2008.
B. Scholkopf, A. J. Smola, K. R. Muller, M. Kybernetik, B. Schlkopf, and K. R. Müller, “Kernel principal component analysis,” Adv. kernel methods Support vector Learn., 1999.
S. Dong et al., “Bearing degradation state recognition based on kernel PCA and wavelet kernel SVM,” Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci., 2015.
X. Jin, L. Lin, S. Zhong, and G. Ding, “Rotor fault analysis of classification accuracy optimition base on kernel principal component analysis and SVM,” in Procedia Engineering, 2011.
V. N. Vapnik, “The Nature of Statistical Learning Theory,” Springer. 1995.
O. P. Yadav, D. Joshi, and G. L. Pahuja, “Support Vector Machine based Bearing Fault Detection of Induction Motor,” Indian J. Adv. Electron. Eng., vol. 1, no. 1, pp. 34–39, 2013.
B. Zhou and J. Xu, “An adaptive SVM-based real-time scheduling mechanism and simulation for multiple-load carriers in automobile assembly lines,” Int. J. Model. Simulation, Sci. Comput., 2017.
D. M. J. Tax and R. P. W. Duin, “Support Vector Data Description,” J. Dyn. Syst. Meas. Control, 2004.
J. Altmann and J. Mathew, “Multiple band-pass autoregressive demodulation for rolling-element bearing fault diagnosis,” Mech. Syst. Signal Process., 2001.

Еще

Статья научная

Bearing fault detection using logarithmic wavelet packet transform and support vector machine

Текст научной статьи Bearing fault detection using logarithmic wavelet packet transform and support vector machine

II. Vibration Database

III. Fault Frequencies of Rolling Element Bearing

V. Feature Ranking And Dimension Reduction Methods

VI. Support Vector Machine

X. Discussion About Result

XI. Conclusion

Список литературы Bearing fault detection using logarithmic wavelet packet transform and support vector machine