Bending of composite timber

Currently, much attention is paid to comprehensive research of composite materials. Thus, in [1] multilayer armor was developed – aluminum oxide ceramics (woven material), reinforced with epoxy resin and aluminum alloy. In [2], the vibrations of a composite beam made of a functionally gradient material in two directions reinforced with carbon nanotubes were studied. In [3], the effectiveness of various schemes for cladding a plate with composite coatings was determined and compared. В [4] исследована устойчивость подкрепленного отсека фюзеляжа самолета, выполненного из композиционного материала, при чистом изгибе и нагружении внутренним давлением. In [4], the stability of a reinforced aircraft fuselage compartment made of a composite material was studied under pure bending and internal pressure loading. In [5], studies of the resistance of the formed composite material under highspeed impact were carried out. In [6], a mathematical formulation of the problem of forced steady-state and natural vibrations of the smart systems under consideration is given, as well as the results of numerical calculations, from which it follows that graphene composites can be used for additional damping of vibrations of smart structures based on piezoelectric elements. In [7], based on the finite element method, a computational algorithm was developed to solve a limited class of problems on the bending of composite plates reinforced with systems of unidirectional high-strength fibers. A model of dynamic deformation and fracture of composite materials has been developed, which takes into account the nonlinearity of impact loading diagrams with hardening depending on the strain rate [8] .

In [9], Yu. N. Rabotnov proposed a model of a composite material with an elastic-plastic binder and elastic fibers. In this case, a constant shear stress acts between the fibers and the binder during loading. Based on this model, this article examines the stress state of a beam made of composite materials. The problem was solved using conservation laws constructed for a system of differential equations describing the stressed state of the beam. The methodology for constructing conservation laws can be found in [10; 11]. Conservation laws make it possible to effectively solve boundary value problems for a number of equations of mechanics of a deformable solid. Examples of solutions for such problems can be found in [12–15].

Formulation of the problem

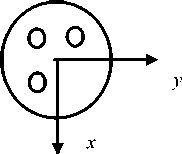
We consider a beam made of elastic-plastic material, reinforced with n elastic fibers. One end of the beam is fixed at point z = 0, at the second end of the beam z = l a load of weight Р is suspended at the origin, which coincides with the center of gravity of the section (Fig. 1).

The timber matrix has an elastic modulus ^G and a pure shear yield strength ^{k s .} The fibers are located along the axis of the beam in a random order parallel to the axis ^z . Each fiber has a circular cross-section, the center of the fiber is located at the point with coordinates ^{( xi , yi ) ,} fi ber radius is ^R , модуль elastic modulus упругости ^G i . The yield strength of the fibers exceeds the yield strength of the matrix. The shear stress between the fiber and the matrix is ^T <  k s •

о о

о

z

P

l

x

Рис. 1. Брус с волокнами с подвешенным грузом

Fig. 1. A fiber beam with a suspended load

The given process is described by the equilibrium equation and the equations of compatibility of deformations [13]:

∂τ _{xz +} ∂τ yz _=- Px ∂ ² τ _{xz +} ∂ ² τ _{xz =-} P       ∂ ² τ _{yz +} ∂ ² τ _yz

∂ x    ∂ y      I ^, ∂ x ²      ∂ y ²      (1 + ν ) I ^, ∂ x ²      ∂ y ²

σ _z

P ( l - z ) x I

I = ∫ x ² ds . S

From the last two equations (1), taking into account the first, we obtain

∂τ xz yz

-

∂ y    ∂ x

P ν

I (1 +ν ) ^y

2 K ,

^{where K} is constant, which is the angle of rotation of the volumetric element of the beam relative to _the a_xis ^z ; ^τ xz ^{, τ} yz ^{, σ} z is stress tensor components; ^S _is beam cross section; I is moment of inertia about the axis ^y ; ν is Poisson's ratio.

The boundary conditions on the side surface of the beam, free from stress and in a plastic state, have the form

τ n +τ m = 0, τ2 +τ2 =k2 =k2 -1/3σ2, xz yz               xz yz            s           z wheren0, m0    components of the normal vector to the lateral surface, which can be written as are

τ _xz = m mk , τ _yz =± nk .                                     (3)

At the boundary between the fiber and the matrix, the following conditions are met:

τxzmi -τyzni =τ, τ2xz + τ2yz =k2, where ni,mi are components of the normal vector to the lateral surface of the i-th fiber, which we write in the form

τ _xz = m_i τ ± n_i 4k ² -τ ² , τ _yz = n_i τ m m_i 7 k ² -τ ².                          (4)

Next, in formulas (3)–(4), the upper sign is selected.

Conservation laws for equations (1)–(2)

For the convenience of further calculations, we introduce the following notation:

τ _xz = u , τ _yz = v .

Then problem (1)–(4) will be written as follows:

F 1 = u x - v y + Px / I = 0,

F = u - v_x--y + 2 K = 0,

• ² y ^x (1 + v/

on the side surface:

u = - mk, v = nk, at the fiber-matrix interface:

u = m i т + n i 4 k² -t ², v = n i т - m i 4 k ² - t ² .

We call the conservation law for the system of equations (5) an expression of the form Definition

A_x ( x , y , u , v ) + B_y ( x , y , u , v ) = « ₁ F ₁ + « ₂ F 2 ,                           (6)

where « 1 , « 2 are some linear operators that are not identically equal to zero at the same time.

More details on the technique of calculating conservation laws and their use can be found in [3–5] . Let it be

A = a ¹ u + p ¹ v + Y ¹, B = a ² u + в ² v + Y 2 ,                             (7)

where ^a i , 3 i , ^у ’ are functions only from x ^{, y} ’

Substituting (7) into (6) we get aX + ay = 0, px + 32 = 0, a1 = «1, p1 = -«2, a2 = «2, 32 = «1,

Y x + у y = -a ¹ Px / 1 + p ¹[2 K - P v y / ( I (1 + v ))].

This implies ax-py = 0, px + ay = 0,

Yx + уy = -a1 Px /1 + p1[2K - Pvy / (I(1 + v))].

for the system of equations we consider (8) two solutions that have singularities ^x 0 ^{, y} 0 at an arbitrary point of the section:

• ¹⁾    1           ^{x - x} 0         _R1_ y ^- y 0

• a               9               9, p                  99,

^{( x - x} 0 ) ^{+ (} y ^- y 0 )          ^{( x - x} 0 ) ^{+ (} y ^- y 0 )

• Y1 = 0,  у2 = -Pxarctg y  y0 +   Pv  (y - y0 + ( y0  + x - x0)arctg y  y0 +

I x - x ₀    I (1 + v )            x - x ₀                x - x ₀

• ⁺ 2 ^{ln(( x - x} 0 ^{) 2 + ( y - y} 0 ^{) 2 ) - K ln(( x - x} 0 ^{) 2 + ( y - y} 0 ^{) 2 )} ,

• ²⁾    „1-        y ^- y 0         R1- ^{x x} 0

• a* —          9             9 , p* —          99 ,

^{( x - x} 0 ) + ^{( y - y} 0 )         ⁽ x ^- x 0 ) + ^{( y - y} 0 )

• Y* = 0,  у2 = 2Karctg y  y0 -   Pv  [y0arctg y  y0 + x—x0ln((x -x0)2 + (y - y0)2)] -

• x - x0   I (1 + v)         x - x02

• ^- Px -^{ln(( x - x} 0 ^{) 2 + (} у ^- y 0 ^{) 2 )} ,

where ^x 0 ^{, y} 0 are constants.

Calculation of the stress state at a point x0 , y 0

Let ^{( x} 0 ^{, y} 0 ⁾ be a arbitrary point belonging to the connector, and let the conserved current at this point have a singularity of the form (9) or (10). Then from (6) it follows

JJ ( A x + B y ) dxdy = J Ady - Bdx - ^ [J Ady - Bdx - [J Ady - Bdx = 0,          (11)

S                        Г0                   i=1 Гi                   ε where ε is circle (x - x0)2 + (y - y0)2 = ε2 (Fig. 2).

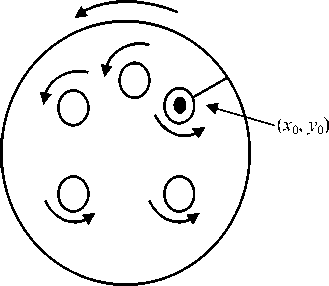
Рис. 2. Вычисление напряженного состояния в точке ^x 0^{, y} 0

Fig. 2. Calculation of the stress state at a point ^x 0^{, y} 0

We consider solution (9), assuming ^x count (9), where ^{ε → 0} , we get

-

^x 0 ^{= ε сos ϕ , y - y} 0 ^{= ε sin ϕ} , then from (11) taking into ac-

2 пт xz ( x 0 , y o ) = J ( m 0 k

Г 0

x - x ₀

( x - x ₀)² + ( y - y ₀)²

- n ₀ k        ^{y - y 0}       ) dy

( x - x ₀)² + ( y - y ₀)²

-

- ( m ₀ k------y—y ⁰----- у + n ₀ k------ x x ⁰ -----— + у ²) dx +

( x - x ₀)² + ( y - y ₀)²       ( x - x ₀)² + ( y - y )²

у J ( ( m i т + n^k ² -T ²)( x - x 0 ) - ( - n i т + m^k² -t ² )( y - y 0 ) ) dy _{i = 1 Г i}    ( x - x ₀)² + ( y - y ₀)²          ( x - x ₀)² + ( y - y ₀)²

- (( m_i τ+ n_i k ² -τ ²)        ^y ₂ ^{- y 0}     ₂ +

( x - x ₀) + ( y - y ₀)

+ ( n_i τ + m_i

k ² -τ ²)       ^{x - x 0}

( x - x ₀)² + ( y - y )²

+ у ²) dx .

We consider another solution to equations (8) of the form (9). Repeating the previous arguments almost verbatim with solution (12), we obtain

^{2 nT} 23 ⁽ x 0 , y 0 ) = J ^{( m} 0 k-------y-y ⁰----- -y ^{+ n} 0 ^k

_{Г 0}       ( x - x ₀)² + ( y - y ₀)²

x - x ₀

( x - x ₀)² + ( y - y ₀)

₂ ) dy -

- ( - m ₀ k

x - x ₀

( x - x ₀)² + ( y - y ₀)²

y - y          ₂

+ n k----------------- — + y* )) dx +

⁰ ( x - x 0 )² + ( y - y )^{2    *}

n

+S J (i=1 Гi

( m_i τ + n_i k ² -τ ² )( y - y ₀) ₊ ( - n_i τ+ m_i k ² -τ ² )( x - x ₀) ( x - x ₀)² + ( y - y ₀)²          ( x - x ₀)² + ( y - y ₀)²

-

) dy -

- ( - ( m t + n^k² -t ² )------ x—x ⁰-----у + ( n t + m_t 4k² -t ² )----- y y ⁰ -----у + у 2 ) dx .

^{i i}           ( x - x 0 )² + ( y - y 0 )^{2      i i}            ( x - x 0 )² + ( y - y )²

Conclusion

The resulting formulas make it possible to calculate the stress state at any point of the binder material. The points where ^T Xz + ^ z = k 2 , will be in a plastic state, other points of the medium, as well as fibers, will remain elastic. The proposed solution method allows us to construct an elastic-plastic boundary in a bendable composite beam and thereby evaluate its load-bearing capacity. The variety of composites [14 – 16] and their enormous practical importance allow us to hope that the methodology proposed by the authors will make it possible to evaluate the strength of structures made from composites.