BER Analysis of Various Channel Equalization Schemes of a QO-STBC Encoded OFDM based MIMO CDMA System
Автор: Husnul Ajra, Md. Zahid Hasan, Md. Shohidul Islam
Журнал: International Journal of Computer Network and Information Security(IJCNIS) @ijcnis
Статья в выпуске: 3 vol.6, 2014 года.
Бесплатный доступ
Quasi Orthogonal Space Time Block Code (QO-STBC) can provide full-rate transmission and low decoding complexity. This paper deals with channel estimation for Quasi Orthogonal Space Time Block Code (QO-STBC) encoded Orthogonal Frequency Division Multiplexing (OFDM) based Multiple Input multiple Output (MIMO) Code Division Multiple Access (CDMA) system. Using the QO-STBC coding property, we analysis the weight performance that reduce the computational complexity of system. The design of channel estimation method is proposed by considering Minimum Mean Square Error (MMSE), Zero Forcing (ZF), and Singular Value Decomposition (SVD) that involves four transmit antennas and four receive antennas. Such filter facilitates the use of standard equalizer or decoder that has been designed to mitigate the Inter Symbol Interference (ISI) effect. In this paper analytical results show that the BER analysis of Minimum Mean Square Error (MMSE) algorithm using various modulation techniques outperforms as compared to other channel equalization techniques.
Code Division Multiple Access (CDMA), Multiple Input multiple Output (MIMO), Minimum Mean Square Error (MMSE), Orthogonal Frequency Division Multiplexing (OFDM), Quasi Orthogonal Space Time Block Code (QO-STBC), Singular Value decomposition (SVD), Zero Forcing(ZF)
Короткий адрес: https://sciup.org/15011283
IDR: 15011283
Текст научной статьи BER Analysis of Various Channel Equalization Schemes of a QO-STBC Encoded OFDM based MIMO CDMA System
Published Online February 2014 in MECS DOI: 10.5815/ijcnis.2014.03.04
By the recent years, the wireless communication become so popular that it is now facing a great challenge to meet the demand to have different types of service in a cost effective way, variety of research is going on worldwide to find out a solution of the ever increasing wish of mankind using the limited source [1].With the technological development, high data rate wireless communications have attracted significant interest and constitute a substantial research challenges in the context of the emerging WLANs and other multimedia networks[2].
In order to meet the increasing demand for cellular mobile communication service around the globe, new digital cellular systems have been introduced during 1990s, and one of the most exciting of the new technologies is CDMA [3] The technology is used in Ultra High Frequency (UHF) cellular system .CDMA has great advantages to increase in capacity, improved call quality, simplified system planning, Bandwidth on demand, enhanced privacy, increased Mobile talk time, etc.
The traditional Time Division Multiple Access (TDMA) and Frequency Division Multiple Access (FDMA), as well as the orthogonal CDMA are orthogonal multiple access [3].In wireless communication, how to efficiently utilize the system resources, such as frequency spectrum and power, and to provide high quality transmission, are the main challenges [4]. CDMA employs Analog to Digital (A/D) Converter in combination with spread spectrum technology. Spread spectrum techniques use a transmission bandwidth that is several orders of magnitude greater than the minimum required signal bandwidth. In a CDMA system, the same frequency can be used in every cell, because channelization is done using the pseudo-random codes. This system uses the soft handoff, which is undetectable and provides a more reliable and higher quality signal.
By using multiple antennas at the transmitter and receiver we can dramatically improve throughput and robustness of wireless communication system [5]. Significant spectral efficiency advantages can be achieved by exploiting the characteristics of MIMO channel [6]. MIMO systems will need to function reliably in an interference limited environment. Multiple antennas can be used at the transmitter and receiver, an arrangement called a multiple-input multiple-output (MIMO) system. A MIMO system takes advantage of the spatial diversity that is obtained by spatially separated antennas in a dense multipath scattering environment. MIMO systems may be implemented in number of different ways to obtain either a diversity gain to combat signal fading or to obtain a capacity gain.
To increase the diversity of the system the multidimensional MIMO channel can be exploited. Generally, there are three categories of MIMO techniques. The first aims to improve the power efficiency by maximizing spatial diversity. Such techniques include delay diversity, space–time block codes (STBC) and space–time trellis codes (STTC) [7].
Diversity is generally considered lower risk and a well known example is space time codes [8] [9]. Space time coding is a promising technique to improve the efficiency and good performance of MIMO-OFDM system. Orthogonal Space Time Block Code (O-STBC) is an important class of space time codes due to its ability to provide optimal transmit diversity by requiring only simple linear processing at the receiver. But to achieve full rate transmission while retaining much of the orthogonally benefits .QO-STBC has been proposed, and also QO-STBC can achieve higher code rates than O-STBC. Using space time coding, for OFDM system with transmit diversity; two or more different signals are transmitted from different antennas simultaneously.
On the other hand, spatial multiplexing divides the incoming data into multiple sub-streams and transmits each on a different antenna. Spatial multiplexing is thus more exciting than spatial diversity from a high data rate point of view, but there is a fundamental tradeoff between them [10]. It can easily adapt to severe channel conditions without the need for complex channel equalization algorithms being employed. With OFDM, we can easily mitigate the ISI because low data rates are carried by each carrier. OFDM involves the transmission of data on multiple frequencies for the duration of a symbol. By using multiple carriers, communication is maintained should one or more carriers be affected by either narrow-band or multi-path interference. A key aspect of OFDM is that the individual carriers overlap to improve spectral efficiency. Normally, overlapping signals would interfere with each other. However, through special signal processing, the carriers in an OFDM waveform are spaced in such a manner that they do not interfere with one another – i.e., they are orthogonal to each other so that there is no crossinterference and hence no signal loss. The key benefits of OFDM include increased spectral efficiency and high resistance to multi-path interference and frequency selective fading. Using OFDM and coding across the frequency band can mitigate narrow-band interference. Indeed, coding and OFDM exhibit a spreading gain similar to spread-spectrum techniques.
MIMO can be used with OFDM to improve the communication capacity and quality. When used in CDMA system; it is possible to minimize interference from neighboring cells by using different carrier permutations between the two cells. And also interference within the cells are averaged by using allocation with cyclic permutation, and offer frequency diversity by spreading the carriers all over the used spectrum [11]. OFDM can achieve, higher spectral efficiency with MIMO CDMA using rake receiver.
This paper investigates Quasi Orthogonal Space Time Block Code (QO-STBC) encoded Orthogonal Frequency Division Multiplexing (OFDM) based Code Division Multiple Access (CDMA) system where a typical 4×4 QO-STBC scheme with four transmit antennas is employed at the transmitter. With 4×4 antennas, we examine here a single user receiver design that includes the channel estimation and symbol detection. Using the Bit Error Rate (BER) computed from Minimum Mean Square Error (MMSE), Zero Forcing (ZF), and Singular Value Decomposition (SVD) on the data matrix, the channel coefficients are estimated by solving a quadratic optimization problem. Based on the QO-STBC property, weighting analysis of the MMSE algorithm out performs as compared to other channel estimation.
The residue of this paper is organized as follows. Section 2 presents the system model of the QO-STBC encoded OFDM based CDMA system over a frequency selective fading channel. Three channel estimation MMSE, ZF and SVD is proposed, the receiver design and weight analysis is performed in section 2.1, 2.2, 2.3 respectively. The simulation result of BER performance for three channel estimation are given in section 3.Finally section 4 contains the conclusions.
Notation : Throughput this paper, vectors and matrices are denoted by boldface lower and upper case letters, respectively; Superscripts of (.) ,(.) T ,(.) H ,(.) + denote the complex conjugate, transpose, complex conjugate transpose, and pseudo-inverse of a matrix, respectively. E [.] denotes the statistical expectation;
-
II. SYSTEM MODEL
Fig. 1 shows a QO-STBC encoded OFDM based
MIMO CDMA system equipped with four transmit and receive antennas. At a transmission time n, a binary data block {b[n, k]; k = 0,1....} is coded into different signals, {t [n, k]; k = 0,1.......} for i = 1,2.........N . So, the encoding and transmission scheme for QO-STBC system is characterized by the following coding matrix [12]:
|
bk (4 n ) |
- b *(4 n + 1) |
- b *(4 n + 2) |
b (4 n + 3) k |
||
|
Bk ( n ) = |
bk (4 n + 1) |
b *(4 n + ) * |
- b *(4 n + 3) * |
- bk (4 n + 2) |
(1) |
|
bk (4 n + 2) |
- b k(4 n + 3) |
b *(4 n ) |
- bk (4 n + 1) |
||
|
bk (4 n + 3) |
b *(4 n + 2) |
b *(4 n + 1) |
bk (4 n ) . |
Where b (n) is the nth information symbol for user k. In our system, we are transmitted single user data through ith transmitted antenna at the nth time slot. Let d(i) (n) be the transmitted symbol and characterized by
dk ( n ) = t dk ( n ) dk(n ) dk ( n ) d 4( n)]T
According to the encoding scheme in (1), the coding matrix is rewritten as
Bk ( n ) = [ d (4 n ) dR (4 n + 1) dR (4 n + 2) dk (4 n + 3) ] (2)
From the encoding and transmission schemes described in (1) and (2), the coding vector d ( n ) satisfies the following relations to design efficient channel estimation and filter design for QO-STBC encoded OFDM based MIMO CDMA system.
d k (4 n ) = bk ( n )
dk (4 n + 1) = MTT b * ( n )
d k (4 n + 2) = m bf n ) (3)
d k (4 n + 3) = m 4 b k ( n )
Where bk ( n ) = [ bk (4 n ).
hk(4n + 3)] T and
M 2 =
- 1
, M 3 =
, M 4 =
0 -
After the spreading and IFFT operations, OFDM based MIMO CDMA transmitted signal is given by
X1 ) ( n ) = L H J\1 ) ( n ) c k 1 ) / N (4)
Where c(k1) = [c(1)(0).....ck1)(N — 1)]^ , the spreading code and F is denotes the N x N DFT Matrix. Considering the channels are selective fading gains and Linear time invariant (LTI), where
h(1 ,Q) = [h(1-q)(0).....h1 - q)(L — 1)T is the channel impulse response from the ith transmit antenna to the qth receive antenna. For the kth user and L is the maximum delay spread among all channels. Cycle prefix is added in this system to avoid the ISI effect whose length is larger than the channel order. After discarding the corresponding CP, the received signal at the qth receive antenna from all transmit antenna is given by
r q ( n ) = ^ K= 5 4.= ^)( n )(*) h ki - q ) + П ( q ) ( n ) (5)
where n = [ П 1 - П 2 - П 3 -.... П n ] T be the uncorrelated
Additive White Gaussian Noise n with variance у 2 n . Now, perform FFT operation on the item Xki ( n )(*) hk ( i , q ) in (5) yields
FFT X ( n X») h k1 - q ) | = d k1 ) ( n ) 0 ( Fh - q ) = d k "( n ) < h kq )
Where FL contains the first L columns of F and c k') is an N x L matrix ck) = diag(ck)(0)........ck4.N — 1))FL ■ Substituting (6)
into (5), the frequency domain received signal at the qth receive antenna is derived by
K 4
y ( q ) ( n ) = Fr ( q ) ( n ) = ^^ d^ 1 ) ( n ) c ( 1 ) h ( 1 - q ) + V ( q ) ( n ) (7)
k = 1 1 = 1
Where V(q)(n) = Fn(q)(n) . Now the signal vector y(n) is expressed as y (n) = ]TAkdk (n) + V (n) (8)
k = 1
The received QO-STBC n-coded OFDM based MIMO CDMA block signal by stacking y ( n ) in four time slots,
Z ( n ) = [ yT (4 n ) yH (4 n + 1) yH (4 n + 2) yT (4 n + 3) ] T is simplified as
K z (n) = ^ Gkbk (n) + n (n) = Gb (n) + n (n) = G (B) + N (9)
k = 1
Gk =[AHM2 ATM3 ATM4 AH ]H and n (n) = VH (4 n), VT (4 n +1), VT (4 n + 2), VH (4 n + 3)]H
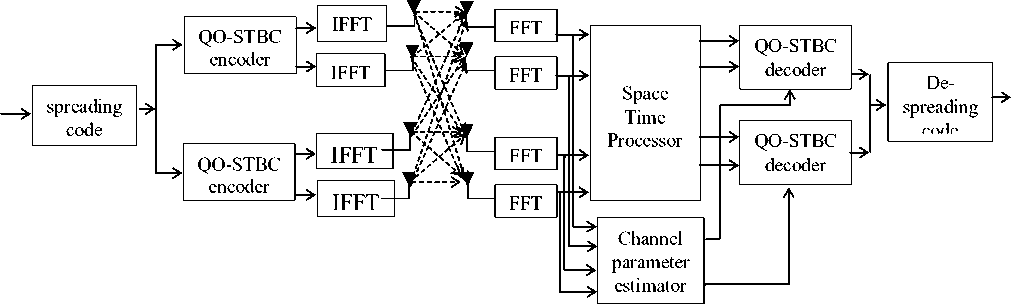
Figure 1. System Model
The matrix G expresses channel impulse responses and spreading vector, and b ( n ) contains QO-STBC symbols for all users.
-
A. MMSE estimation
MMSE analysis of channel estimation of received data y(n) in (8) is shown in Fig.2 and goal to estimate ■. •: using the estimator y(n) = g(y(n)) . The optimization criterion is to minimize the expected error, E { X (n) - y (n ))2 }= E { X (n) - g (y (n )))2 } (10)
Normally, g ( y ( n )) is dependent on a parameter vector Ф .
Where g ( y ( n )) = g ( y ( n ), ф )
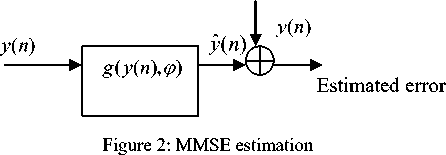
Now, the MMSE estimator, фMMSE = argф minE{(X(n) - g(y (n). ф))2} (11)
y( n ) = g ( y ( n )) = ay ( n ) + b; Ф = [ a , b ]
e (a, b ) = E {(X (n) - ay (n) - b )2 } фmmse = [a b»] = arg[ a, b ] mine( a, b) (12)
Taking partial derivative of (12) then
Ц = E{2(X(n) - ay(n) - b).(-y(n))} da
= - 2 E { x ( n ) y ( n ) - 2 aE { y ( n ) } 2 + 2 bE { y ( n )} } = 0
Or, aE { y ( n ) } 2 + bE { y ( n ) } = E { y ( n ) X ( n ) } (13)
And similarly, b = E { X ( n ) } - aE { y ( n ) } (14)
Combining (13) and (14)
aE { ( y ( n ))2 }+ E { y ( n ) } E { X ( n ) }- a [ E { y ( n ) }] 2 = E { y ( n ) X ( n ) }
Or, a =
E { y ( n ) X ( n ) }- E { y ( n ) } E { X ( n ) } = Cov(X ( n ) y ( n)) E { ( y ( n ))2 } - [ E { y ( n ) } ] 2 Var ( y ( n ))
= p y ( n ) X ( n ) ^ X ( n ) CT y ( n )
and b = E { X ( n ) } - p y ( n ) X ( n ) X ( n ) E { y ( n ) } (16)
CT y ( n )
-
B. ZF estimation
With a zero forcing (ZF) equalizer, the tap coefficients w are chosen to minimize the peak distortion to of the equalized channel, characterized by
N + L - 1
D p = ш El q n - q n l (17)
I q d n = 0
n ^ d
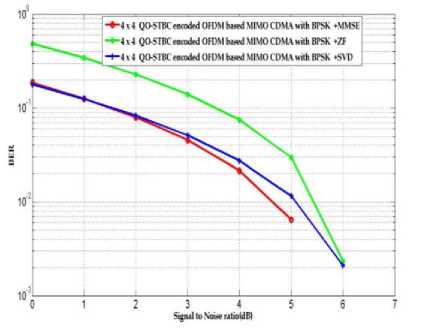
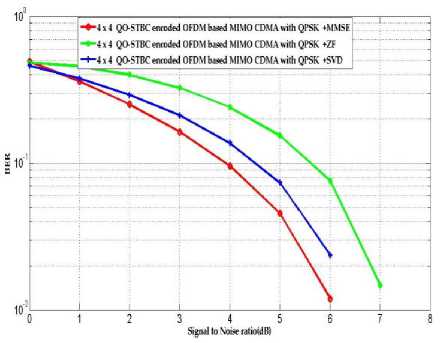
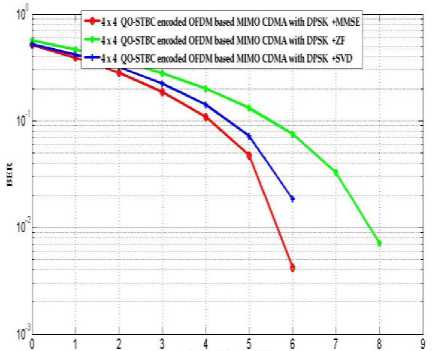
Where q = ( During the training mode when the channel impulse response is unknown to the receiver and a is used as known finite length sequence, the equalizer can be obtained by using the following steepest descent recursive algorithm: wn+1 = wn+ aenan- j-dx, j = 0,....., N-1 (18) And en = an - d - an N-1 = an -d -E wiyn i=0 Where {wn} is the set of equalizer tap gains at epoch n and a is an adaption step size. The adaption rule in (18) attempts to force the cross correlations snan-j-d,j = 0,......N -1, to zero. C. SVD estimation From (9) where B = [b(0) b(T -1)], where T is the QO-STBC blocks, contains the transmitted symbol. If the noise component from (9) is ignored, the SVD of the data matrix is expressed by Z=[■»Г 0 L 5 N о 0 [vSvN Y Where VS = [4,......... .,v4k]is the signal subspace, Vn = [v4 k+1,.......',4 N9 ] is the noise subspace, £s = diag(ni,.....П4k) But noise is present in the system and data matrix in (9) is corrupted by noise, the SVD of Z becomes. A En [vSvN H The final MSE calculation is given by III. COMPUTER SIMULATIONS Consider the QO-STBC OFDM based CDMA systems with four transmit antennas and four receive antennas. The transmit symbol adopts the BPSK, QPSK and DPSK modulation scheme and spreading codes of length N = 32 are used. The input signal-to-noise ratio (SNR) is defined as the bit SNR at each receive antenna, which is given by, SNR( dB) = 10log1 (T-XPK V un Where TX indicates the number of transmit antenna. The quality of the channel estimation is measured by the root mean square error (RMSE), which is defined as RMSE = 17T Tlhk (m)- hk(m )l V mm =1 Where Nm is the no. of Monte-Carlo-runs, hˆk (m) and hk(m) are the estimated channel and the true channel at the mth runs respectively [13][14]. The proposed system is simulated in MATLAB and the simulation parameters are given in Table 1 [15]. TABLE 1. Simulation parameters Parameters Details No. of bits 1024 SNR 0-10 dB Energy per bit 0.5 Modulation and Demodulation BPSK, QPSK, DPSK Channel Equalization Sheme MMSE, ZF, SVD Spreading Code Walsh-Hadamard Code Wireless Channel AWGN, Rayleigh Processing Gain 8 States for random number generator 4831 FEC Code Trellis Code Fig. 3, Fig. 4, and Fig. 5 shows the BER performance of QO-STBC encoded OFDM based MIMO CDMA system are computed from MMSE, ZF, and SVD channel estimation on the data matrix, the channel coefficients are estimated by solving a quadratic optimization problem with diversity according to BPSK, QPSK and DPSK modulation respectively. The weight performance is analyzed to reduce the computational complexity in this system. The three channel estimation techniques MMSE, ZF, SVD are used with three modulation schemes which have been designed to combat the ISI. In Fig. 3 shows the filtered output signal of BPSK modulation where considering the SNR value at 4dB and the BER values of MMSE is 0.0054, SVD 0.0055 and ZF approximately 0.01. The system achieves a gain of 4dB in MMSE and SVD as compared to ZF. Figure 3: BER Analysis of QO-STBC encoded OFDM Based MIMO CDMA in BPSK with three channel estimation. In Fig. 4 shows the results of QPSK modulation where we consider the SNR value is 4dB and the BER values of MMSE are 0.0054, SVD 0.0055 and ZF approximately 0.01 which is very similar the model of using BPSK modulation scheme. Here it is also seen that the system achieves a gain of 1.01 dB in MMSE as compared to SVD and also 1.81dB in SVD as compared to ZF at SNR value of 4dB [16]. Figure 4: BER Analysis of QO-STBC encoded OFDM Based MIMO CDMA in QPSK with three channel estimation. In Fig. 5 presented the results of DPSK modulation where at the same SNR value (4dB), the BER performance of MMSE is 0.01, SVD 0.012 and ZF approximately 0.015 which shows the bit error rate is increased than using BPSK and QPSK modulation scheme. Signal Io Noise ratioWB) Figure 5: BER Analysis of QO-STBC encoded OFDM Based MIMO CDMA in DPSK with three channel estimation. IV. CONCLUSION We have presented a good trade-off between performance and complexity. Further from the analysis, it was identified that MMSE with BPSK and QPSK modulation combining techniques provides reduced error rate and is the best opted combining technique.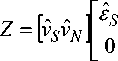
Список литературы BER Analysis of Various Channel Equalization Schemes of a QO-STBC Encoded OFDM based MIMO CDMA System
- Husnul Ajra, "Performance Evaluation of a QO-STBC Encoded OFDM Based MIMO CDMA Wireless Communication system With Various Channel Equalization Schemes", Rajshahi University , M.Sc Thesis - 2010.
- Theodore S. Rappaport,Wireless Communication principles and practice, 2nd Edition, Prentice Hall India.
- CDMA T&C Lesson 1, "http://wireless-resource.blogspot.com/2012/07/what-is-cdma-advantage-disadvantage-and_4266.html".
- Qi Qu, Laurence B. Milstein, and Dhadesugoor R. Vaman, "Cognitive Radio Based Multi-User Resource Allocation in Mobile Ad Hoc Networks Using Multi-Carrier CDMA Modulation", IEEE journal on communications, vol. 26, No. 1, January, 2008.
- Wan Choi, Jeffrey G. Andrews, "Spatial multiplexing in cellular MIMO-CDMA systems with linear receivers: Outage probability and capacity," to appear (2004) Cached, Venue: IEEE Trans. Wireless Comm, Citations: 7 - 4 self.
- G. J. Foschini and M. J. Gans, "On limits of wireless communications in a fading environment when using multiple antennas," Wireless Personal Commun., vol. 6, pp. 311-335, March 1998.
- H. Bolcskei, D. Gesbert, and A. Paulraj, "On the capacity of wireless systems employing ofdm-based spatial multiplexing," IEEE Trans. Commun., vol. 50, no. 2, pp. 225-234, Feb. 2002.
- S. M. Alamouti, "A simple transmit diversity technique for wireless communications," IEEE Jour. Select. Areas in Commun., vol. 16, no. 8, pp. 1451-1458, Oct. 1998.
- V. Tarokh, N. Seshadri, and A. R. Calderbank, "Space-time codes for high data rate wireless communication: Performance criterion and code construction," IEEE Trans. Info. Theory, vol 44, no. 2, pp. 744-765, Mar. 1998.
- Gordon L. Stuber, John R. Barry, Steve W. Mclaughlin, I. Mary Ann, AND Thomas G. Pratt, "Broadband MIMO-OFDM Wireless Communications", proceeding of the IEEE , Vol. 92, No. 2, February 2004.
- L. Zheng and D. Tse, "Diversity and multiplexing: A fundamental tradeoff in multiple antenna channels," IEEE Trans. Info. Theory, vol. 49, no. 5, pp. 1073-1096, May 2003.
- Jafarkhani H. "A quasi-orthogonal space-time block code" IEEE transaction on communications, vol-49, pp. 332-335, 2001.
- Wang Z., Giannakis GB, "Wirelees multi carrier communications: Where Fourier meets Shannon", IEEE signal processing magazine, vol-17, No-3, pp. 29-48, 2000.
- Ari H, olav T, Risto W., "Multi-antenna Transceiver techniques for 3G and beyond", Wiley: Newyork, NY, 2003.
- H. Zahid, H. Reaz, "Performance evaluation of a concatenated FEC scheme based Wimax system with applicaion to the digital image transmission over white guassian noise and fading channels", Asian journal of information technology, vol 9(2), pp. 62-66, 2010.
- H. Zahid,A. Nur-E-Zaman and R. Hasibur, "Precise BER Analysis of 1/2 and 2/3 rated RS-CC Concatenated Coded for Digital Image Transmission in OFDM System", International journal of computer science issues, vol. 9, Issue 5, pp. 119-125, September 2012.


