Бесконтактное прецезионное измерение линейных смещений с использованием ДОЭ, формирующих моды Бесселя

Существуют немало оптических методов бесконтактного измерения линейных смещений. Наиболее известные - проекционный и интерферометрический. Проекционный метод позволяет измерять линейные смещения в диапазоне от 0,01 мм до 103 мм с точностью ~ 0,001 мм – 0,1 мм [1]. При этом используются измерительные микроскопы или длинномеры. Для достижения высокой точности измерений используются возможности человеческого глаза, что затрудняет автоматизацию этого метода. Автоматизированные системы, основанные на проекционном методе, позволяют определять линейные смещения с погрешностью около 0,01 мм [2, 3]. При этом с увеличением измеряемого смещения растет абсолютная ошибка измерения. Интерферометрический метод позволяет измерять линейные смещения в диапазоне от 10-4 мм до 10-2 мм с точностью ~ 10-4 мм [4]. При этом абсолютная ошибка измерения практически не меняется. Как видно, эти два метода работают в совершенно разных диапазонах величин измеряемых линейных смещений. Между этими диапазонами есть довольно большой разрыв, то есть. смещения, размер которых лежит в диапазоне от 10-2 мм до 10-1мм, сложно измерять с помощью одного из этих методов. Необходим метод, который позволял бы измерять линейные смещения вэтом диапазоне. В качестве такого метода в данной работе предлагается использование пучков, обладающих вращением вокруг оси распространения. Простейшие из них — суперпозиция двух бесселевых функций с разными показателями и масштабами. Для измерения линейных смещений рассмотрены вращающиеся бесселевы пучки, сформированные с помощью бинарных фазовых ДОЭ с пространственной несущей частотой [5,6].

Эксперимент

ДОЭ устанавливается в оптическую схему (рис. 1), которая состоит из самого ДОЭ, He-Ne-лазера, зеркала и телекамеры, которая регистрирует пучок отраженный зеркалом. ДОЭ имеет размер 4×4мм, разрешение – 4×4 мкм, глубина фазовой решетки 1,26 мкм. При освещении ДОЭ гауссовым R пучком на расстоянии z =    ≈ 4мм , где ψ - угол tgψ наклона конической волны к оси распространения пучка, формируется почти бездифракционный вращающийся двухмодовый пучок Бесселя с номерами мод (n, m)=(-1,0)+(2,1). В центральной части сечения пучка имеет место распределение интенсивности в виде трех пятен в диаметре каждый около 200 мкм.

Распределение интенсивности в сечении пучка вращается равномерно, и по известному периоду поворота и углу поворота можно определить линейное смещение зеркала ∆l :

∆ l =∆ ϕ ^L                             (1)

Φ

где Φ – угол повторения изображения, L – период расстояния вдоль оси повторения изображения, ∆ϕ - угол поворота изображения. Причем угол повторения изображения совершенно необязательно должен быть равен 2 π , так как обычно изображение моды имеет несколько осей симметрии.

телекамера

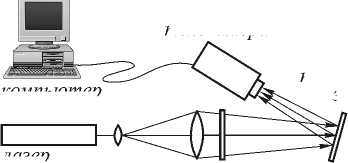
компьютер лазер коллиматор ДОЭ

Рис. 1. Оптическая схема устройства для измерения линейных смещений.

подвижное зеркало

Для определения линейных смещений в данном устройстве использовался ДОЭ с периодом повторения L =10 мм. Этот ДОЭ строит изображение, которое имеет три оси симметрии. То есть угол повторения изображения равен ² π ₃ . Был проведен эксперимент на упрощенной оптической схеме, которая приведена на рис. 2.

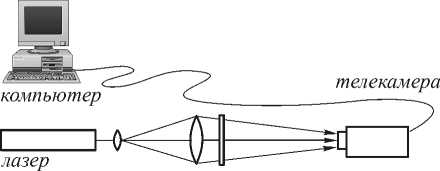
коллиматор   ДОЭ

Рис. 2. Оптическая схема, используемая в эксперименте.

В ходе эксперимента телекамера смещалось микрометрическим винтом, и регистрировались изображения через 0,5 мм. Размерность регистрируемых изображений составляла 512 × 512 пикселов. Реальный размер изображения - около 0,5 мм. На рис. 3 приведены несколько таких изображений для смещений 0 мм, 0,5мм, 1мм и 1,5мм

Из-за расплывчатых краев светлых пятен изображения точное измерение угла поворота невозможно. Для измерения угла поворота определялись координаты центра тяжести светлых пятен x , y по формулам:

1 AA x = —у J JI (x, y)xdxdy A2 00

• 1    ^{AA               ,}

y = — J J I ( x , y ) ydxdy A 00

где A – размер изображения, I(x,y) – функция яркости изображения.

а)                        б)

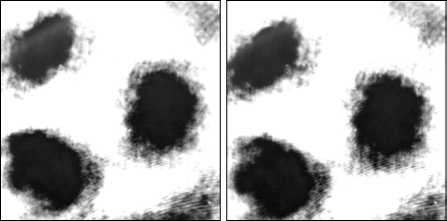
• в)                           г)

Рис. 3. Информативная часть изображения в исходной плоскости (а), со смещением 0,5 мм (б), со смещением 1 мм (в), со смещением 1,5 мм (г).

Затем определялось среднее расстояние от центров светлых пятен до центра тяжести по формуле между отрезками, которые соединяют точку x, y и границы пятна в кольце.

r =

1 AA              2         2

— J J I ( x , y )J( x - x ) 2 + ( y - y ) 2 dxdy . ^{A 2} 00

На исходном изображении выделялось узкое кольцо с центром в x , y и радиусом r (рис. 4). На этом кольце определялись границы одного из пятен. Направлением на пятно считается биссектриса угла.

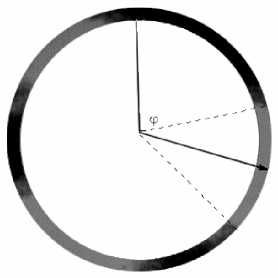
Рис. 4. Измерение угла поворота по обработанному изображению.

На рис. 5 представлены графики функции средней интенсивности измеряемой в кольце с радиусом r для двух плоскостей измерения, расстояние между которыми составляет 0,5 мм.

Всего в ходе эксперимента проведено 20 смещений на 0,5 мм. Было установлено, что минимально определяемое угловое смещение составляет 0,08 или 3,8% от периода, тогда минимально

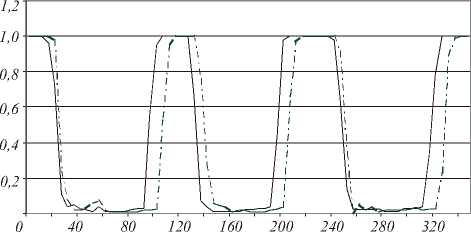
Рис. 5. Графики функции средней интенсивности в зависимости от угла, который отсчитывается от центра тяжести.

определяемое смещение составляет 0,38 мм. Так как теоретически размер периода можно существенно уменьшить, то соответственно будет уменьшаться и размер минимального смещения, которое можно определить в данном устройстве. Был проведен вычислительный эксперимент, в котором моделировалась работа оптической схемы на рис. 2. В ходе эксперимента был рассчитан ДОЭ со следующими параметрами: размер элемента – 2 мм, размерность матрицы отсчетов для ДОЭ 1024 x 1024 период полного поворота – 0,2 мм, число светлых пятен в информативной части изображения - 3.

На рис. 6 показаны несколько изображений полученных в вычислительном эксперименте для смещений 0 мм, 0,1 мм, 0,2 мм.

а)                   б)                   в)

Рис. 6. Информативная часть изображения на исходной плоскости (а), со смещением 0,1 мм (б),

со смещением 0,2 мм (в).

Размер изображения 0,5 мм. Погрешность измерения линейного смещения (или минимально обнаруживаемое смещение) составляет 2,5% от периода или 0,005 мм. Эта погрешность сопоставима с погрешностью проекционного метода [2]. При этом расстояние, на котором пучок сохраняет свою структуру, составляет 12 мм. То есть максимальное смещение, которое может быть измерено этим методом составляет 12 мм. Разрешение, которое необходимо для изготовления этого ДОЭ, составляет 2 мкм, что не является пределом для современной технологии изготовления ДОЭ. Так что в перспек- тиве можно получить существенно меньшую погрешность для этого метода. К сожалению, возможности компьютера не позволяют провести вычислительный эксперимент для ДОЭ с меньшим периодом полного поворота. В качестве дополнительной возможности для уменьшения погрешности следует указать возможность измерения угла поворота усредненного по нескольким светлым пятнам.

Заключение

Проведенные исследования подтверждают перспективность использования фазовых ДОЭ, формирующих вращающиеся пучки в измерительной технике. Особый выигрыш в точности измерения достигается в диапазоне измерений от 10-3 мм до 10-1 мм.