Бесконтактный экспресс-контроль взаимного положения рельсов железнодорожной колеи

Ширина железнодорожной колеи определяет безопасность движения транспорта. Рельсы имеют большую протяжённость, подвержены динамическому и климатическому воздействию. Сбор информации об их состоянии для систем управления движением поездов осуществляется с помощью диагностических вагонов-лабораторий, выполняющих комплексную компьютерную диагностику железнодорожного пути с помощью электромеханических сканирующих систем [1]. Наличие стрелочных переводов рельсовой колеи требует одностороннего размещения датчиков над рельсом, что определяет актуальность разработки многоканальной системы автоматического бесконтактного экспресс-контроля взаимного положения рельсов.

Электромагнитные методы контроля применяются в различных отраслях промышленности для бесконтактного измерения перемещений и геометрических параметров изделий сложной формы. Для одновременного контроля большого количества факторов используется многоточечный контроль, при котором над контролируемой поверхностью необходимо разместить не менее nраб = br/bм преобразователей, где br – ширина верха головки рельса, а bм – ширина одиночного накладного преобразователя (ПН). Надёжная работа преобразователей требует их установки с максимальным вертикальным зазором безопасности hz н. В методе вихревых токов широко используются компланарные ПН, конструктивные особенности которых не позволяют разместить большое количество преобразователей, обеспечивающих высокое значений hz н, в зоне контроля. Рассматриваемый матричный вихретоковый преобразователь (МВП) включает большое количество катушек индуктивности с сильной электромагнитной связью, что позволяет получить новые характеристики преобразователей и обеспечить измерение геометрических параметров объекта контроля в широком диапазоне изменения их значений.

Контролируемые факторы и размещение устройства контроля над колеёй

Определение ширины колеи b кл в процессе движения подвижного состава требует размещения устройства контроля на тележке вагона-лаборатории. В системе координат X ₀ Y ₀ Z ₀, связанной с колёсной парой, фиксируем координаты центров рабочих поверхностей корпусов ПН левого и правого рельсов колеи, как объекта контроля (ОК), задающих системы координат XYZ преобразователей (рис. 1, 2, система координат X 0 Y 0 Z 0 не показана). Ширина b кл может быть определена как линейные перемещения h y лр , h y пр и ширина b r лр , b r пр левого и правого рельсов:

кл кт ко ш yлр ₂ rлр yпр ₂ rпр ^, где b кт – расстояние между внутренними торцами колёс, b ко – ширина колеса, b ш – ширина металлического корпуса ПН, рабочая поверхность которого параллельна плоскости XY , представляющие собой конструктивные параметры.

Вертикальное h z и горизонтальное h y перемещения поверхности катания каждого рельса относительно преобразователей вычисляются автономно, как отклонения систем координат X_rY_rZ_r , связанных с серединой поверхности катания рельсов от систем координат XYZ преобразователей: h z = z – h z н , h y = y .

Ширина b ш корпуса ПН должна быть больше суммы ширины b r рельса и диапазона h y max поперечных перемещений: Ь ш >  b r + h y max , а для безопасности работы при движении вагона-лаборатории b ш меньше ширины b ко колеса вагона.

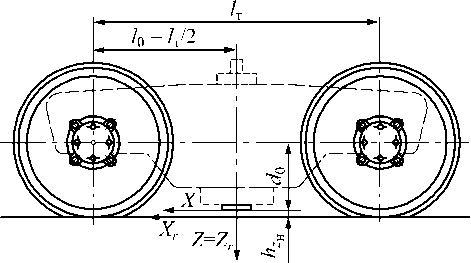
Рис.1. Установка корпуса преобразователей на тележке вагона-лаборатории

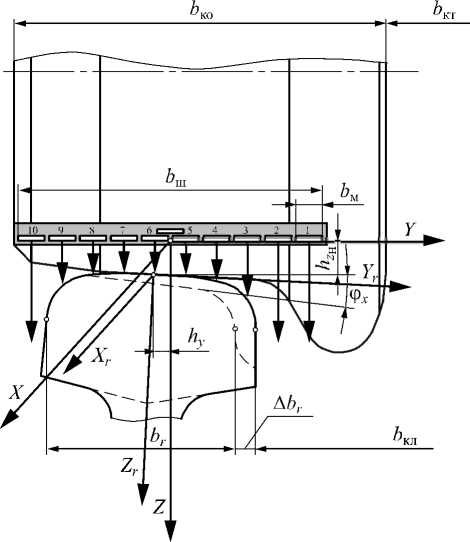
Рис.2. Взаимное положение рельса и преобразователей

Средние преобразователи удалены от краев рельса и имеют доминирующую чувствительность к вертикальным перемещениям h z . Крайние преобразователи, расположенные вблизи краёв рельса, чувствительны к h z и h y . Установка промежуточных преобразователей позволяет дополнительно контролировать угловые отклонения поверхностей катания рельса и колеса, влияющих на динамику износа профиля рельса. Угловое положение можно определить по формуле:

h - h ф_х = arctg —    "пл- ,

Ьф

где h zпп , h zпл – текущие вертикальные зазоры промежуточных ПН; Ь _ф - расстояние между их центрами.

Таким образом, задача сводится к определению значений вектора P = ( h z , h y , b r , ф x ), задающего геометрические параметры рельса в пространстве факторов. Размещение n_раб преобразователей в малой зоне контроля требует разработки матричных электромагнитных преобразователей.

Конструкция матричного вихретокового преобразователя

В работе [2] проведена идентификация электромагнитных преобразователей по параметрам конструктивной топологии. Для компланарных ПН (рис. 3 а ) диапазон контролируемых перемещений связан с величиной диаметра эквивалентного контура вихревых токов D э « D_K , где D_K - диаметр катушки ПН, и коэффициентом связи K т :

Dэ = , т 6\  т , Kт = Lbh/Lbh„ , ln L - ln L            1 m внm          вн

где L_{вн m} – максимальная, а L_вн – текущая вносимые индуктивности преобразователей. Диаметр D _э ® Ь к характеризует ослабление поля с увеличением h z , а коэффициент связи K т — величину вносимых параметров преобразователей при зазоре h z н . Диаметр D э компланарных ПН определяется меньшей стороной b к прямоугольного токового контура, поэтому при больших h z н над поверхностью рельса возможна установка только одного преобразователя.

Размеры корпуса ПН выбираются так, что высота катушки d_к всегда намного меньше глубины d_z установочного паза, иначе вихревые токи экрана ослабляют возбуждающее поле ПН. Использование n раб значительно увеличивает габариты корпуса экранированных преобразователей, что исключает возможность применения ПН в труднодоступных зонах.

Для контроля поверхности конструктивных элементов применяют матричные вихретоковые преобразователи (МВП). Известны МВП, разработанные компанией ASEA-Brown Boveri, представляющие собой трансформаторные преобразователи на мягкой подложке [3]. ПН установлены так, что их взаимное влияние минимально. При этом ограничивается возможность выполнения контроля взаимосвязанных факторов.

Решение поставленной задачи достигается использованием экранированных ортогональных преобразователей (рис. 3б). Изменяя соотношение площадей lхb, lxd, bxd, определяющих электромагнитное поле ПН по заданному направлению, можно осуществить многовариантность соотношений чув-ствительностей к контролируемым факторам. Длина 1м « Dэ магнитопровода катушки определяет дальнодействие возбуждающего электромагнитного поля преобразователя. Длина рельса намного превышает lм, а потому легко реализуется заданный диапазон hz max изменений зазоров между поверхностью катания рельса и преобразователями.

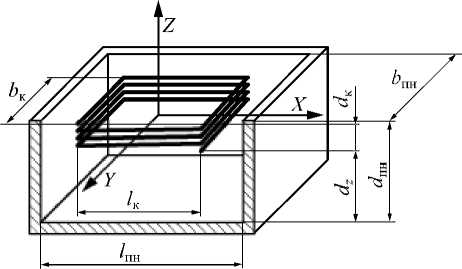
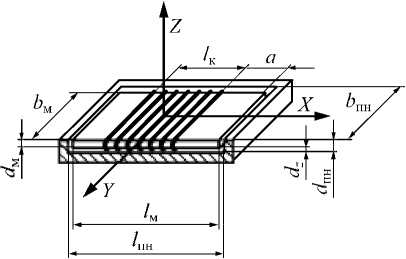
Рис.3. Конструктивные размеры компланарных и ортогональных ПН

Многоточечный контроль геометрических факторов определяет использование модульного принципа схемно-конструктивной компоновки ортогональных ПН, который позволяет:

• 1.    организовать переменную или периодическую структуру возбуждающего электромагнитного поля, исходя из задач контроля и особенностей форм изделия;

• 2.    повысить производительность контроля путем выбора рационального количества унифицированных модулей ортогональных ПН и зон контроля;

• 3.    получить повышенные К т и D э каждого ПН к контролируемому фактору;

• 4.    использовать интегральную технологию изготовления катушек ортогональных ПН с магнитопроводом;

• 5.    размещать ПН в пазах единого проводящего корпуса для локализации электромагнитного поля в зоне контроля и снижения погрешности от взаимного влияния пространственных компонент перемещений и от других факторов, например, температуры;

• 6.    получить новые характеристики преобразователей, позволяющие расширить функциональные возможности средств.

Применение модульного принципа компоновки МВП позволяет реализовать пространственную селекцию влияющих факторов за счёт увеличения ny = bш/bм количества ПН, а размещение их в прово- дящем корпусе устройства экранирует ПН, что локализует поле в зоне контроля и снижает влияние внешних полей на погрешности измерений. ПН расположены в плоскости и образуют дискретную шину с общим электромагнитным полем, что обеспечивает высокое значение Dэ.

Расчёт индуктивности сильносвязанных электромагнитных преобразователей

Исследование характеристик преобразователей выполнено на основе численных расчётов начальных L_н и вносимых L_вн индуктивностей каждого преобразователя МВП. При этом магнитный поток, создаваемый ТЭ дискретной шины, удобно представить в виде совокупности элементарных трубок с малым сечением A S м и постоянной напряжённостью H магнитного поля. Начальная индуктивность L н ПН составляет:

• n_x m_z m_y         n_xn_y m_z m_y

к = Z | ZZ Ф. + £И фД I к ,     (2)

i V 11    111 л где ф = ц Hi ASM - магнитный поток, создаваемый i-м ТЭ; Ф – магнитный поток, создаваемый j-м ТЭ ijм и охватывающий i-й ТЭ; (nxхny) - количество ТЭ дискретной токовой шины в плоскости оси XY; mz, my – количество трубок магнитного потока в направлении осей Z и Y. Количество nx = 1к/А 1к определяется шагом А 1к размещения ТЭ вдоль оси X по длине lк катушки ПН, а ny – количество ПН, образующих МВП.

Элементарную топологию магнитного поля имеет вихретоковый преобразователь в виде проводника Ь ш ^ «. Если направление тока совпадает с осью Y , то в плоскости Х0Z силовые линии плоскопараллельного поля представляют семейство окружностей, задающих трубки возбуждающего магнитного потока. В плоскости Y0Z проекции силовых линий определяют дальность D э действия поля, а их угловое положение принимаем за нулевое направление Ф и = 0. Величина сечения магнитного потока ТЭ определяется его длиной b м и дальнодействием поля: S_м = b_мD_э .

Исследование параметров электромагнитного поля ТЭ осложняется его трёхмерным характером. Известно много компьютерных программ (ANSYS, FEMLAB, ELCUT и др.), которые автоматически разбивают моделируемое пространство на конечные элементы при заданных границах сечений магнитных потоков. Однако для рассматриваемой задачи границы полей автономных ПН неизвестны, что требует разработки новых алгоритмов численных расчётов их характеристик. Расчет функций пространственного распределения магнитного поля токовых элементов, с использованием принципа суперпозиции полей, показывает, что магнитные трубки с большой плотностью магнитной энергии обладают повышенным давлением p = 0,5 ц ₀ H ² .

Поэтому в плоскости Z0Y наклон силовых линий трубок ф и увеличивается с удалением Y зоны контроля поля. Следовательно, необходимо учитывать увеличение b s трубки при удалении по Z и Y , т. е. поле каждого ТЭ размером b м имеет переменное сечение магнитного потока (рис. 4).

Расчёт напряжённости H магнитных потоков ТЭ, представленных совокупностью n x х n y линейных проводников конечного размера b м , выполнен с помощью закона Био-Савара: dH = I_Kdb_M х h 0/ 4 п| h |³ , где I_кdb_м – ТЭ, создающий напряжённость H в рабочем пространстве, а h – радиус-вектор, проведённый от ТЭ в точку определения напряжённости H поля. Сечение трубки A S_м = A b s A h z , где A b s , A h z -ширина и высота элементарной трубки магнитного потока.

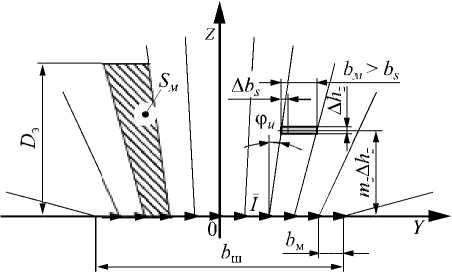
Рис.4. Сечения магнитных потоков ПН шины

Для расчёта Фis количество mz трубок магнитного потока в направлении оси Z составляет mz = (о.51м -|xkJ//axк , где l. - длина магнитопровода; хк - координата i-го ТЭ ПН; Ax к - шаг размещения ТЭ вдоль оси X. Для расчёта Ф исполь-ijм зуем выражение mzj = |xKj - хк|/Axк , где хк - координата j-го ТЭ ПН.

Для определения границ синфазных квазиста-ционарных конструктивно неограниченных электромагнитных полей ПН используется условие:

k             n y

2 h.= 2 н.

1               к + 1

где 2 k H_x . , 2 k + ₁ H x - суммы напряжённостей полей ПН, расположенных соответственно слева и справа от границы между k -м и ( k +1)-м преобразователями; k – порядковый номер ПН в МВП. Проекция силовых линий магнитной индукции на плоскость YZ , определяемая по условию (3), имеет нелинейный характер, но на рабочем участке может быть аппроксимирована прямыми линиями (рис. 4). Ширина сечения b s = f ( h z ) определяется как:

• b = b„ + m, A h,\tg ф„ - tg ф , (4) s ki м z ki z g ^ф ик g ^ф и к - i ’

где ф , ф - углы отклонения проекций силовых и к и к - 1

линий магнитного потока от нормали к ТЭ k и k -1 преобразователей. Выражение (4) позволяет определить количество m_y учитываемых трубок магнитного потока вдоль оси Y : m y = b s I A b s . Погрешность численных расчётов индуктивности ПН зависит от выбора A b s . Однако уменьшение A b s ведёт к существенному росту времени вычислений.

Вносимая индуктивность ПН определяется вихревыми токами, наводимыми на поверхности ОК. Разбивая русло вихревых токов на дискретные элементы, определяем величину тока на участках поверхности рельса:

( nxny      1

i e Ф2 ^Hx |a i e ,

I      1          J где A 1в - шаг дискретизации токовых элементов русла вихревых токов на поверхности ОК. Вносимая индуктивность Lвн вычисляется по аналогии с (2):

n x n в x n в y m z m y

L bh = 2 222 Фк м к ,            (5)

• ¹ 1 ¹¹¹    )/

Ф_{ik м} – магнитный поток, создаваемый k -м ТЭ русла вихревых токов и охватывающий i -й ТЭ дискретной шины. Используя (2) и (5), для результирующей индуктивности преобразователя имеем:

L p = L h — L «h .

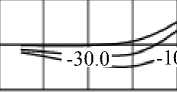
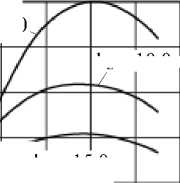
Рассмотренный подход расчёта индуктивности сильносвязанных электромагнитных преобразователей реализован в программе моделирования полей дискретной токовой шины [4], с помощью которой получены характеристики U_eH = f(h z , h y , p x ), показывающие, что линейное размещение преобразователей позволяет получить различные чувствительности к контролируемым факторам, обеспечивающие пространственную селекцию геометрических параметров рельса. На рис. 5 показаны расчётные графики функций распределения вносимых индуктивностей L вн / L вн m = f(h y ) ПН при вариации h z . Из графиков видно, что максимальное значение L вн / L вн m = f ( h z ) имеет преобразователь, расположенный над серединой ОК (средний ПН — y к = 30 мм). Для ПН, находящихся над краями ОК, функция L_вн / L_{вн m} = f ( h_y ) имеет наибольшую крутизну.

Использование выражений (2), (5) при вариации значений вектора P = ( h z , h y , b_r , ф _x ) позволяет моделировать полевое взаимодействие МВП и ОК. Графики функций L вн / L вн m = f ( h y , h y ) существенно отличаются от характеристик слабосвязанных ПН. Анализ функций L вн / L вн m = f ( h y ) (рис. 5) показывает, что для преобразователей, находящихся за пределами ОК, L р >  L н . В соответствии с (3), данный результат можно объяснить тем, что компенсация возбуждающего поля, закрытого ПН полями вихревых токов ОК при   h z ^ 0 уменьшает 2 H_x ,

Sм действующую на поле соседнего открытого ПН, при этом сильное увеличение ∑ S ∆Sм открытого ПН м

приводит к росту его L p , что позволяет сделать вывод о доминирующем влиянии S м на величину L р .

b ш = 100.0 мм;

b м = 10.0 мм;

l к = 50.0 мм;

b r = 60.0 мм;

h y = 30.0 мм;

ϕ x = 0.0°

^L вн_i ^L внm

0.6

0.4

0.0

0.2

h z = 5.0

h z = 15.0

h z = 10.0

-0.2

10.0

30.0 y к , мм

Рис.5. Функции распределения вносимой индуктивности L_вн/L_{вн m} = f ( h_y ) при вариации h_z

Специализированный лабораторный стенд вихретокового контроля геометрических параметров объектов

Для проверки достоверности полученных теоретических результатов создан лабораторный стенд, учитывающий особенности разработанного МВП, структурная схема которого показана на рис. 6.

Разработанный МВП расположен над рельсом 1 и состоит из рабочих 2 и компенсационного 3 преобразователей, которые размещены в едином проводящем корпусе. Высокое значение частоты f генератора 5 соответствует распределению вихревых токов только на поверхности ОК, с глубиной проникновения d_эм → 0 . Для синфазного возбуждения переменных полей все преобразователи питаются от источника постоянного напряжения 8, а переменные токи создаются переходными колебательными процессами при коммутации цепи питания с LC -контурами с помощью синхронных ключей 4, управляемых от генератора 5. Преобразователи имеют одинаковое значение начальной индуктивности L_н . Период колебаний LC -контуров с рабочим и компенсационным преобразователями составляет T = 2 π L C и T = 2 π L C .

р   рк   к

В устройстве 6 формирования выходных напряжений определяется разность ∆ T = T_к – T_р и выполняется усреднение ∆ T = ∑ ₁ ⁿ ∆ T_i !n , что позволяет снизить случайные погрешности. Выходной сигнал каждого измерительного канала определяется как U = U эт ∆ T/ T_s , где U эт – напряжение источника питания; T s – период, задаваемый генератором 5. Выходные напряжения U i передаются в компьютер 7 для последующей обработки.

В качестве ОК использовались модели в виде плоских пластин различной ширины b r , выполненные из алюминиевого сплава. Перемещения h z , h z , ϕ x ОК относительно МВП задавались с помощью инструментального микроскопа ММИ-1.

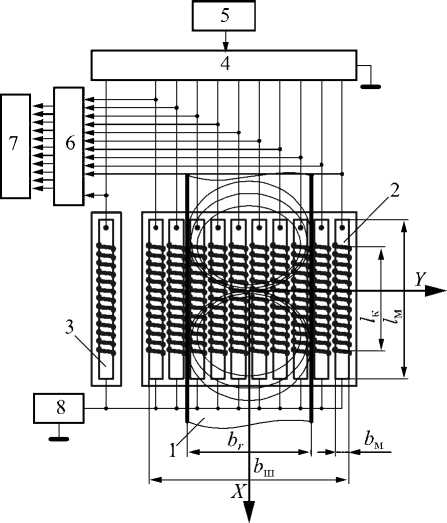
Рис.6. Структурная схема устройства контроля

На рис. 7 показана совокупность нелинейных характеристик U i = f ( h y ) сильносвязанных ПН МВП, полученных на лабораторном стенде. При перемещении h y ОК относительно МВП только n раб ПН расположены над контролируемой поверхностью.

Основная погрешность δ _Σ измерения:

δΣ = 7δс2л+ δr2+ δ2нл , где δсл – случайная погрешность, обусловленная слабо действующими факторами; δr – погрешность гистерезиса; δнл – погрешность нелинейности характеристик функций отклика. Ввиду усреднения Ui величиной δсл пренебрегаем. Погрешностью δr также пренебрегаем. Учитывается только погрешность δнл нелинейности при кусочно-линейной аппроксимации характеристик функции отклика, которая должна быть меньше допустимой и определяет шаг дискретизации по контролируемым факторам.

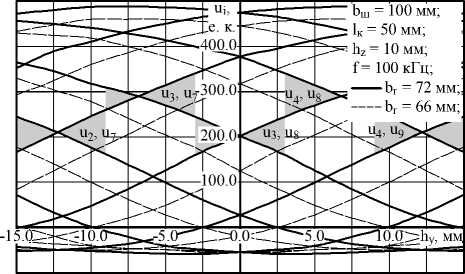
Рис.7. Характеристики U_i = f ( h_y ) градуировочных массивов данных

Массив градуировочных сигналов относится к так называемой обучающей выборке. Объём N массива градуировочных сигналов

^ = ny ( npz ■ npy ■ npb ■ Пр ф ), где ny – количество измерительных каналов, npz, npy, npb, np(p - количество градуировочных точек по каждому фактору, определяемое шагом дискретизации градуировочных характеристик. Для заданных диапазонов изменения контролируемых факторов и выбранных шагов их дискретизации с учётом переналадок стенда общее время градуировки превышает 4 часа.

В алгоритмических методах процедура обработки экспериментальных данных формулируется как задача распознавания образов, в которой вектор контролируемых факторов P s = P ₀ + A P s , где A P s -отклонение вектора P_s контролируемых факторов от известного положения P ₀ в факторном пространстве. Представим вектор сигнальных напряжений U ( P s ) как отклонение от вектора напряжений U ( P ) в градуировочной точке P ₀ факторного пространства:

U(P + AP) = U(P) + VUAPs +s , где U (P0 +APs ) = U (Ps) - вектор сигнальных напряжений ПН блока; V U - матрица, определяющая чувствительность ПН по каждому контролируемому фактору; £ - погрешность определения факторов. Выражая отклонение APs, получим:

APs =(VU)"' [U (P +APs)- U (P)] .

В линейном п р иближении, выбирая малый шаг дискретизации A P факторного пространства, в котором чувствительность ПН к каждому фактору остаётся постоянной. Тогда коэффициенты K = ( k z , k y , k_b , k _p ) отклонения вектора U ( P s ) от U ( P ) равны коэффициентам отклонения P_s от P ₀ . Для определения K по всем факторам выбираем дополнительные точки факторного пространства, отстоящие на шаг градуировки от P ₀ и ближайшие к P_s . В каждой такой точке имеем вектора напряжений:

U ( P z ) = U ( h z 0 ±A h z , h y 0 , b r 0 , ф X 0 ),

U ( P y ) = ^U ( h z 0 , h y 0 ±^A h y , Ь ^ , ф , ₀ ),

U ( P b ) = U ( h z 0 , h y 0 , b r o ±^A b r , ф X o ),

U ( P ) = U ( h , h , b_r , ф ± Aф ).

X ^ф /         X z 0 - ^y 0 - ^r0 7 T ^X 0        T ^X /

Используя вектора напряжений (6), составляем систему линейных уравнений:

U (Ps)-U (P ) = kz (U (Pz)-U (P)) +

+ k y (U ( P y ) - U ( P ) ) + k b (U ( P b ) - U ( P ) ) + (7)

+ kф (U (Pф)-U (P)), из которой находим коэффициенты отклонений вектора сигнальных напряжений по всем факторам. Количество уравнений соответствует количеству ny ПН, поэтому система линейных уравнений (7) является переопределённой. Значения коэффициентов K определяем методом наименьших квадратов, реализованным во многих широко распространённых программах обработки экспериментальных данных. Условием существования решения системы (7) является наличие известных и различных Ui = f (P), что обеспечивается заданной асимметрией в пространственном размещении ПН МВП относительно контролируемых факторов, приводящей к отличию от нуля функционального определителя (Якобиана):

d ( u 1 , u 2 , ^ , U n )/ d ( h z , h y , b r , ф x ) * 0.

При этом шаг размещения ПН в МВП определяется величиной b м , связанной с начальным зазором безопасности h z н .

Каждый фактор определяется как:

hz = hz 0 + kz A hz , hy = hy 0 + kyA hy , br = br0 + kb Abr , ф X = фX0 + kФAФ X .

Программное обеспечение [5] лабораторного стенда реализовано в среде Matlab с помощью интерпретатора со встроенного языка программирования вычислений, что позволяет без дополнительной перенастройки стенда изменять алгоритм обработки измерительных сигналов ПН. Быстродействие разрабатываемого устройства экспресс-контроля определялось с помощью специально разработанного тестового модуля. Время измерения составляет 20 мс, что при скорости движения подвижного состава 100 км/ч составляет не менее 15 отсчётов по длине рельса.

Выводы

Проведённый в ходе исследований сравнительный анализ известных систем контроля перемещений и геометрических параметров верха головки железнодорожного рельса в загрязнённой среде показывает перспективность разработки и применения матричных вихретоковых преобразователей в устройствах многофакторного экспресс-контроля железнодорожной колеи. Выделенные контролируемые факторы характеризуют состояние (образ) рельса в колее.

Разработана математическая модель для численных расчётов электромагнитных полей матричных преобразователей, реализованных на дискретных токовых элементах. В отличие от известных моделей расчёт индуктивностей выполнен на основе оценки границ сечений конструктивно неограниченных магнитных потоков сильносвязанных преобразователей.

Разработан компьютеризированный лабораторный стенд для экспериментальных исследований и градуировки многоканальной аппаратуры контроля перемещений и геометрических параметров объектов сложной формы, работающий в широком диапазоне линейных и угловых перемещений. Полученные характеристики подтверждают достоверность теоретических расчётов. Алгоритм определения контролируемых факторов, представляющих образ объекта контроля, включает в себя решение системы линейных уравнений. Предлагаемое устройство позволяет повысить экономическую эффективность экспресс-контроля состояния железнодорожной колеи за счёт снижения затрат на оборудование диагностической системы.

Работа выполнена в соответствии с протоколом о намерениях по внедрению устройства экспресс-контроля железнодорожной колеи, заключённым с филиалом ОАО «РЖД Куйбышевская железная дорога». Лабораторный стенд используется в учебном процессе.