Бездифракционные асимметричные элегантные пучки Бесселя c дробным орбитальным угловым моментом

Известно [1], что уравнение Гельмгольца

( V ² + k 2 ) E ( x , y , z ) = 0,                               (1)

где k = 2π/λ – волновое число монохроматического света с длиной волны λ, в цилиндрической системе координат ( r , φ, z ) имеет решение в виде мод Бесселя

E n ( r, ф , z ) = exp ( ikz cos 6 ₀ + in ф ) J_n ( kr sin 6 ₀), (2) где θ ₀ – угол конической волны, формирующей пучок Бесселя, J n ( x ) – функция Бесселя первого рода n -го порядка. Угол θ 0 определяет амплитуду спектра плоских волн моды Бесселя (2) на единичной сфере F_n ( 6 , ф ) = (- i ) ⁿ exp ( in ф ) 5 ( 6 - 6 ₀), где 5( x ) - дельта-функция Дирака. Моды Бесселя (2) имеют бесконечную энергию и при распространении в однородном пространстве сохраняют свою интенсивность (квадрат модуля амплитуды (2)), и поэтому называются без-дифракционными пучками Бесселя [2]. Линейная комбинация решений (2) уравнения (1) с произвольными коэффициентами также является решением уравнения (1). В [3] предложен алгоритм расчёта фазового оптического элемента, который формирует бездифракционные пучки Бесселя с заданным модовым составом:

^

E ( r , ф , z = 0) = E C n exp ( in ф ) J n ( kr sin 6 0 ).       (3)

n =0

В [4] предложено рассматривать пучок Матье как альтернативу пучку Бесселя:

E n ( S , П , z ) = Ce n ( S , q ) ce n ( n , q ) exp( ikz cos 6 0 ),      (4)

где Сe n (ξ, q ), ce n (η, q ) – непериодическая и периодическая функции Матье. Решение (4) является решением [1] уравнения (1) в эллиптической системе координат:

x = d ch S cos П , y = d sh S sin П , z = z ,

q = ( kd sin 6 ₀)² / 4.

В [5] показано, что линейная комбинация чётного и нечётного пучков Матье

E n ^{( S} , n , z ) = Ce n ^{( S} , q ) ce n ⁽ n , q ) ⁺ + iSe n ( S , q ) se n ( n , q ), n >  2

имеет n изолированных нулей c единичным топологическим зарядом одного знака, лежащих на горизонтальной оси x внутри первого светлого эллиптического кольца. То есть линейная комбинация (6) пучков Матье (4), которые не обладают орбитальным угловым моментом (ОУМ), обладает ОУМ. Интересно [6], что линейная комбинация, аналогичная (6), двух мод Эрмита– Гаусса, которые не обладают ОУМ, обладает ОУМ.

Периодические функции Матье можно разложить в ряд Фурье [1], например, чётные функции:

^

ce 2 n ( ф , q ) = E A 2 m ⁽ q ) cos (2 m ф ),                    (7)

m =0

коэффициенты ряда (7) вычисляются рекуррентно. Используя (7), бездифракционный пучок Матье (4) можно представить как линейную комбинацию мод Бесселя:

E 2 n ( S , П , z ) = exp ( ikz cos 6 0 ) x

^

XE (-1Г A22m cos ( 2mФ) J2m ( kr sin 60 ), m=0

где (ξ, η, z) и (r, φ, z) – эллиптические и цилиндрические координаты. В [7] рассмотрены бездифракцион-ные пучки, описываемые в виде линейной комбина- ции мод Бесселя (8). Фактически пучки (8) - это пучки Матье (4) в цилиндрических координатах.

Интересно найти линейные комбинации мод Бесселя (3) или (8), которые бы описывались простыми аналитическими функциями, с помощью которых можно было аналитически рассчитать некоторые свойства таких бездифракицонных пучков. Например, в данной работе рассматривается линейная комбинация мод Бесселя (2) с такими коэффициентами, что ряд (3) вычисляется и равен функции Бесселя с комплексным аргументом. Показано, что такой бездифракционный элегантный пучок Бесселя (ЭБ-пучок) имеет счётное число изолированных нулей интенсивности, расположенных на оси x вблизи нулей моды Бесселя наименьшего порядка в линейной комбинации. Все эти нули (кроме осевого) порождают оптические вихри с единичным топологическим зарядом и противоположными знаками с разных сторон от начала координат. Нуль интенсивности на оптической оси порождает оптический вихрь с топологическим зарядом n . Точно рассчитан ОУМ таких пучков - он оказался дробным.

1. Нули ЭБ-пучков

Рассмотрим следующую суперпозицию мод Бесселя:

E n ( Г , ф ,₌ = 0 ) = t exp ( in ^'p * ’ J. + p ( a r ) .     (9)

p =0         p !

Поле (9) формирует бездифракционную моду Бесселя при любых целых n . Интересно, что амплитуда (9) явно не зависит от длины волны %, а только через параметр а = k sin 9₀ = (2п / a ) sin 9₀. То есть для любой длины волны можно подобрать угол 9₀, чтобы параметр а не изменился и пучок Бесселя (9) остался тем же. В произвольной плоскости, поперечной оптической оси z , такие пучки будут иметь следующую комплексную амплитуду:

E n ( r , ф , z ) = exp

( bjk ² -a ² z ) x

x t ^exp ( in ^ф+ .^{р ф}) J n + p ( „ r ) . p =0         p ^!

Мы рассматриваем линейную комбинацию мод Бесселя в виде (9), потому что этот ряд равен функции Бесселя с комплексным аргументом. Действительно, в [8] есть справочный ряд (выражение 5.7.6.1):

^ ,k

t ^k + ^ ( X ) = k=0 k !

= x^{v /2} ( x - 2 1 )^- v ² J_v (V x ² - 2 tx ) .

С помощью (11) преобразуем (9):

. (                  exP ( in ^ ^{+ 1} p ф ) T ( \

En ( r, ф, Z = 0 ) = t-------,------Jn+Р (“ r ) = p=0        Г ■ ar ar - 2exp (i ф)

- n / 2

x

x Jn {.J ar [ar - 2 exp (iф)] } exp (inф).

Функция Бесселя в правой части (12) не будет расходиться на бесконечности, так как все экспоненты и функции Бесселя в левой части (12) по модулю не превышают единицы, а значит, весь ряд не превышает числа e. Когда знаменатель в (12) равен нулю, тогда и аргумент функции Бесселя равен нулю. Не- определённость ноль на ноль раскрывается. Нули

ЭБ-пучка (12) лежат на оси x (при ф = пm, где m = 0, 1, 2, ...) в точках с координатами:

= ^{1 +} 71+Y p a ’

^x + p

x >  0;

^x - p

^{1 -} yi+z p a

x <  0, p = 1,2,3,...

В (13) y _p - это корни функции Бесселя: J_n ( y _p )=0. Из (13) следует, что интенсивность в сечении ЭБ-пучка несимметрична относительно начала координат, так как x +p >- x _ _Р . Все нули ЭБ-пучка (кроме осевого при r =0) порождают оптические вихри с единичным топологическим зарядом и противоположными знаками с разных сторон от начала координат. При x <0 топологический заряд оптических вихрей +1, при x >0 - топологический заряд -1. Действительно, рассмотрим выражение под корнем в аргументе функции Бесселя в (12). Если корень x = y _Р >2/ а , то при начале обхода вокруг этого нуля полярный угол меняется в диапазоне 0< ф <  п /2 и под корнем в аргументе функции Бесселя в (12) получим: ( a r )² 2( a r )cos ф - i2( a r )sin ф = x -i y (оптический вихрь с топологическим зарядом -1). Если корень x =у _p <0, то при начале обхода вокруг этого нуля полярный угол запишем в виде ф = п + ф , где ф меняется в диапазоне 0 <  ф <  п /2, и под корнем в аргументе функции Бесселя в (12) получим: "( a r )²+2( a r )cos ф + i 2( a r )sin ф = x +i у (оптический вихрь с топологическим зарядом +1).

Чтобы сменить знаки этих оптических вихрей на противоположенные, надо вместо (12) взять комплексно сопряжённое выражение. Ноль интенсивности в (12) на оптической оси порождает оптический вихрь с топологическим зарядом n .

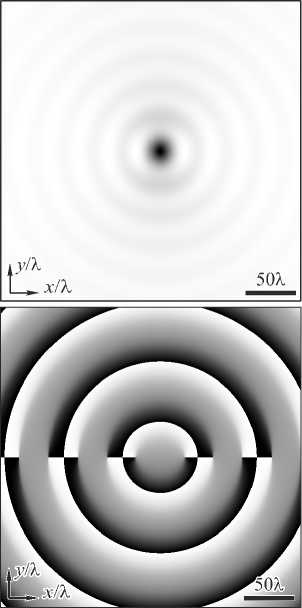
Эти выводы можно проверить, рассматривая фазы на рис. 1 и 2. На рис. 1 и 2 для различных значений параметров показаны интенсивности световых пучков (12) в начальной плоскости, а также сечения интенсивности при z = у = 0 и z = x = 0. При моделировании были использованы следующие значения параметров: длина волны света % = 532 нм, масштабирующий множитель a = 0,2 (мкм)^-1, границы расчётной области 150 % <  x , у < 150 % , число отсчётов по каждой оси N =200. На рис. 1, 2 порядок пучка n = 0, 3.

ЭБ-пучок нулевого порядка (рис. 1) обладает интересным свойством: имеет максимум интенсивности и ОУМ, отличный от нуля (он будет вычислен ниже). Это свойство можно использовать при манипулировании диэлектрическими микрочастицами. Частица, которая по размерам в несколько раз больше основного максимума интенсивности пучка на рис. 1, может удерживаться этим максимумом интенсивности и одновременно вращаться вокруг своей оси.

б)

Ж

в)

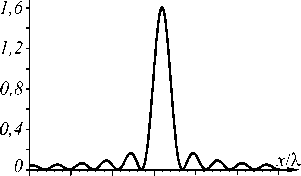
Рис. 1. Интенсивность (негатив) (а) и фаза (б) светового пучка (12) нулевого порядка (n = 0) в начальной плоскости, а также сечения интенсивности при z = y = 0 (в) и z = x = 0 (г). Чёрный цвет (б) соответствует фазе, равной нулю, белый цвет - фазе, равной 2п

Из рис. 1 в видно, что максимальное значение ЭБ-пучка нулевого порядка

E о ( r , ^ф) = J о {7 “ r ^{[ а} r ^{- 2ex}P ( i ^ф) ^] } ⁽¹⁴⁾ больше единицы: I _max=1,6. Этому есть объяснение. Так как при a r <2 и ф = 0 аргумент (14) чисто мнимый, то на этом участке оси х ЭБ-пучок нулевого порядка можно представить как

E о ( r , ф ) = I о {V « x (2 -а х ) } , (15) где 1 ₀ ( х ) - модифицированная функция Бесселя нулевого порядка.

б)

0,2

0,1

50 100 уIX

г)

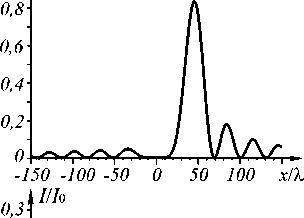
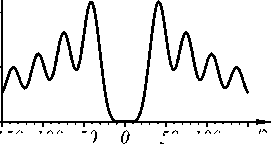
Рис. 2. Интенсивность (негатив) (а) и фаза (б) светового пучка (12) третьего порядка (n = 3) в начальной плоскости, а также сечения интенсивности при z = y = 0 (в) и z = x = 0 (г). Чёрный цвет (б) соответствует фазе, равной нулю, белый цвет - фазе, равной 2 п

На концах отрезка [0, 2/а] аргумент функции (15) принимает значение ноль, а сама функция Бесселя равна J0(0)= 10(0)=1. На этом отрезке [0, 2/а] функция (15) достигает максимума в точке, в которой аргумент достигает максимума. А аргумент достигает максимума в середине отрезка, то есть при х = 1/а. В этой точке функция (15) равна E0(r = 1 /а, ф = 0)=10(1) = 1,266. Поэтому максимальное значение интенсивности ЭБ-пучка равно Imax =|Eа(r = 1/ а, ф = 0)|2 = 12(1) = 1,60. Из этого, в частности, следует, что максимальная интенсивность боковых лепестков ЭБ-пучка нулевого порядка (14) (рис. 1), которая совпадает с максимальной интенсивно- стью боковых лепестков для обычного пучка Бесселя J0(x), составляет меньшую часть от максимальной интенсивности в основном лепестке для ЭБ-пучка (10%), чем для обычного пучка Бесселя (16%).

На рис. 2 видно, что основной лепесток ЭБ-пучка высокого порядка имеет вид «полумесяца», выпуклого в правую сторону. Можно записать выражение для ЭБ-

пучка, имеющего вид «полумесяца», выпуклого в левую сторону. ЭБ-пучок, имеющий распределение интенсивности, зеркально-симметричное относительно оси x =0 по сравнению с пучком (12), имеет амплитуду вида:

E n ( r , Ф )

^

=z

p =0

( - 1) p exp [ i ( n + p ) ф ]

p !

J n + p ^{( a r} ) =

ar ar + 2 exp (i ф)

n /2

X

X J

n

{^ a r [ a r + 2 exp( i ф ) ] } exp ( in ф ).

На рис. 3 для тех же значений параметров, что и на рис. 1 и 2, показаны интенсивность и фаза светового пучка (16) в начальной плоскости, а также сечения интенсивности при z = y =0 и z = x =0. На рис. 3 порядок пучка равен n =4.

2. Угловой спектр плоских волн ЭБ-пучка

Подставим угловой спектр пучка Бесселя F_n ( 9 , ф ) = ^ ( — i ) n /( 2 n sin 9 0 ) ] exp( in ф ) 8 ( 9 — 9 0 ) в каждое слагаемое ряда в левой части (12), получим:

” (— i) n+p exp Г i (n + p )ф!

A(9,ф) = Z     7w , - A N —9o) =

„-o       2 n p !sin 9

^p =0                    ⁰                        (17)

(— i) n=          exp [ in ф — i exp (i ф)] 8(9 —90).

2 n sin 9 0

Действительно, при подстановке (17) в разложение по плоским волнам в цилиндрических координатах ( r , ξ, z )

E n ( r , ^ , z ) = j j A ( 9 , ф ) X

0 —n

X exp |^ ikr cos ( ф — ^ ) sin 9 + ikz cos 9 J X

X sin 9 d 9 d ф , получается (12).

3. Орбитальный угловой момент ЭБ-пучка

Орбитальный угловой момент J z (проекция ОУМ на оптическую ось) и суммарная интенсивность I све-

тового пучка в плоскости, поперечной оптической

оси, определяются по формулам [6]:

Jz = Im (jj E * —r dr dф| = U2   дФ

{R 2n lim   E*

R ^^

d E

—rdrdm Эр

I = jj E * Er dr dp= lim j j E * Er dr dp.     (20)

B ²                    R ^“ 0 0

б)

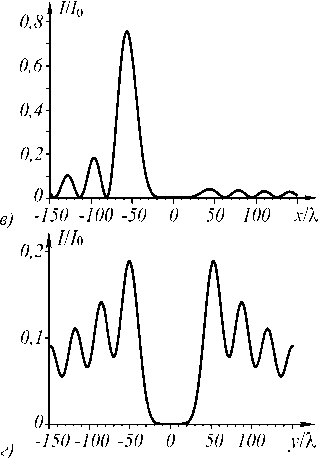
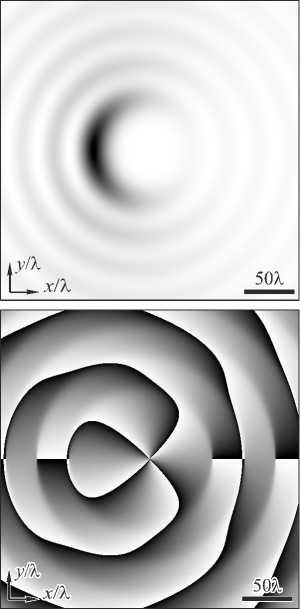
Рис. 3. Интенсивность (негатив) (а) и фаза (б) светового пучка (16) четвёртого порядка (n = 4) в начальной плоскости, а также сечения интенсивности при z = y = 0 (в) и z = x = 0 (г). Чёрный цвет (б) соответствует фазе,

равной нулю, белый цвет - фазе, равной 2 п

Подставив в (19), (20) комплексную амплитуду из левой части (12), получим орбитальный угловой момент и суммарную интенсивность ЭБ-пучка:

R

Jz=2п lim Z     j Jn+p (a r) r dr,

R ^ p =0 ( p ! ) 0

1 R

I = ^{2 n} li^m Z      j ^Jn + p (^{a r} ) ^{r d r} .            ⁽²²⁾

R ^“ p =0 ( p ! ) 0

Интегралы в этих выражениях описаны в [9] (выражение 5.54.2):

J Jp (ar)r dr = r2

= 2[Jp (ar)-Jp-i (ar) Jp+i (ar)].

Используя асимптотику функции Бесселя при больших значениях аргумента (выражение 9.2.1 в [10]), получим, что все интегралы в (21) и (22) не зависят от порядка функции Бесселя и равны R/( па ). Тогда , используя числовые ряды 0.246.1 и 0.246.2 из [9] и разделив (21) на (22), получим выражение для орбитального углового момента , нормированного на интенсивность :

I2

-= = n +     = n + 0,69777,                (24)

I        I 0 ( 2 )

где I_n ( z ) – модифицированная функция Бесселя.

Из (24) следует, что ОУМ ЭБ-пучков дробный и линейно возрастает с порядком n . Из (24) также следует, что ЭБ-пучок нулевого порядка тоже имеет ОУМ, равный J z / I = I 1 (2) / I 0 (2) = 0,69777 . При численном расчёте (по формулам (19) и (20)) получилось для параметров n = 8, % = 532 нм, a = 0,2 (мкм)^-1, -150 % <  x , у < 150 % , N =400, что ОУМ равен J z /I = 8,667 и отличается от ОУМ, рассчитанного по формуле (24) J z /I = 8,6977, всего на 0,3%. Заметим, что подход для расчёта ОУМ, использованный в этом разделе, применим для расчёта ОУМ любого светового поля, представленного суперпозицией мод Бесселя.

4. Ортогональность ЭБ-пучков

Подобно тому, как в предыдущем разделе был вычислен орбитальный угловой момент, можно вычислить скалярное произведение двух ЭБ-пучков – пучка n -го порядка с параметром а и пучка m -го порядка с параметром р :

^ 2п

( E n а , E m _Р) = J J E na E^ r ^d r ^d V =

. 5(a-PL

= ^{2 П} _a I n — ” ^{( 2 )} .

где I_n-m ( x ) – модифицированная функция Бесселя.

Из выражения (25) видно, что в отличие от мод Бесселя ЭБ-пучки ортогональны только по масштабирующему множителю и не ортогональны по порядку функции Бесселя.

Заключение

В работе получены следующие результаты:

– получено новое решение уравнения Гельмгольца, описывающее двухпараметрическое семейство без-дифракционных непараксиальных асимметричных элегантных пучков Бесселя, комплексная амплитуда этих пучков описывается функциями Бесселя первого рода целого порядка с комплексным аргументом (уравнения (12), (16));

– распределение интенсивности ЭБ-пучков в плоскости, перпендикулярной оптической оси, имеет счётное число изолированных нулей, лежащих на горизонтальной оси x; этим нулям соответствуют точки фазовой сингулярности волнового фронта, имеющие единичный топологический заряд (за исключением осевого нуля интенсивности); знак топологического заряда отличается для точек, расположенных с разной стороны от оптической оси (уравнение (13)); осевой ноль интенсивности имеет топологический заряд, равный порядку функции Бесселя;

– ЭБ-пучки имеют кольцевой спектр по углу, задающему направление волнового вектора, и только распределение фазы по полярному углу (уравнение (17)); – ЭБ-пучки имеют дробный ОУМ, который растёт линейно с ростом номера моды (уравнение (24)); пучок нулевого порядка имеет максимум интенсивности вблизи оптической оси и изолированные нули интенсивности вблизи нулей моды Бесселя и обладает ОУМ, равным 0,69777 h на один фотон;

– функции, описывающие комплексные амплитуды ЭБ-пучков, ортогональны по непрерывному параметру (масштабирующему множителю) и не ортогональны по целому параметру (топологическому заряду, уравнение (25)).

Работа выполнена при поддержке грантов Президента РФ поддержки ведущих научных школ (НШ-3970.2014.9) и молодого доктора наук (МД-1929.2013.2), а также грантов РФФИ 13-07-97008 и 14-07-31092.