Безмассовая частица Штюкельберга, решения с цилиндрической симметрией
Автор: Семенюк О.А., Плетюхов В.А., Бурый А.В., Ивашкевич А.В., Редьков В.М.
Журнал: Известия Коми научного центра УрО РАН @izvestia-komisc
Рубрика: Научные статьи
Статья в выпуске: 4 (62), 2023 года.
Бесплатный доступ
Безмассовое поле Штюкельберга исследуется в цилиндрических координатах. Полевая функция состоит из скаляра, 4-вектора и антисимметричного тензора. Физически наблюдаемыми величинами являются только скаляр и 4- вектор. Используется матричное уравнение Штюкельберга, обобщенное на произвольное риманово пространство, в том числе и на любые криволинейные координаты пространства Минковского. Строятся решения этого уравнения с цилиндрической симметрией, при этом диагонализируются операторы энергии, третьей проекции полного углового момента и третьей проекции импульса. После разделения переменных в цилиндрической системе координат получена система из 11 дифференциальных уравнений по полярной координате. Она решается с использованием метода Федорова-Гронского. В соответствии с этим методом, 11 функций выражаются через три основные. По известной методике накладываются дифференциальные условия связи, которые совместны с полученными 11 уравнениями и позволяют преобразовать эти уравнения в алгебраические. Эта алгебраическая система решается стандартными методами. В результате найдены пять независимых решений. Вопрос об устранении калибровочных степеней свободы будет рассмотрен в отдельной работе.
Безмассовое поле штюкельберга, цилиндрическая симметрия, метод проективных операторов, точные решения
Короткий адрес: https://sciup.org/149143596
IDR: 149143596 | УДК: 539.12 | DOI: 10.19110/1994-5655-2023-4-69-76
Текст научной статьи Безмассовая частица Штюкельберга, решения с цилиндрической симметрией
В настоящей работе будем находить все независимые точные решения обобщенного 11-мерного уравнения Даффина–Кеммера для безмассового поля Штюкельберга [1–8]. Система тензорных уравнений для этой частицы име-
Massless Stueckelberg particle, solutions with cylindric symmetry
O.A. Semenyuk1, V.A. Pletyukhov1, A.V. Bury2, A.V. Ivashkevich2, V.M. Red’kov2
-
1Brest State University named after A.S. Pushkin, Brest, Belarus
-
2B.I. Stepanov Institute of Physics of the National Academy of Sciences of Belarus, Minsk, Belarus
The massless Stueckelberg field is studied in cylindrical coordinates. The field function consists of the scalar, 4 -vec-tor, and antisymmetric tensor. Physically observable components are the scalar and 4 -vector. We apply the Stueckelberg tetrad-based matrix equation, generalized to arbitrary Riemannian space, including any curvilinear coordinates in the Minkowski space. We construct solutions with cylindric symmetry, while the operators of energy, of the third projection of the total angular momentum, and the third projection of the linear momentum are diagonalized. After separating the variables we derive the system of 11 first-order differential equations in polar coordinate. It is solved with the use of the Fedorov–Gronskiy method. According to this method, all 11 functions are expressed through 3 main funcions. According to the known procedure we impose the differential constraints, which are consistent with the all 11 equations and allow us to transform these equations to algebraic form. This algebraic system is solved by standard methods. As a result, we obtain 5 linearly independent solutions. The problem of eliminating the gauge solutions will be studied in a separate paper.
∂ a Ψ a = 0 , ∂ a Ψ + ∂ b Ψ ab = Ψ a ,
∂ a Ψ b - ∂ b Ψ a = 0 . (1)
В качестве волновой функции будем использовать 11-мерный столбец
Ф = (Ф; Ф о , Ф 1 , Ф 2 , Ф э ; Ф о1 , Ф 02 , Ф оз ,
Ф 23 , Ф з1 , Ф 12 ) = ( H,H 1 ,H 2 ) . (2)
Система уравнений (1) может быть представлена в блочной матричной форме:
L 2
|
0 |
0 |
0 |
0 |
|
- 1 |
0 |
0 |
0I |
|
I0 |
0 |
0 |
0I |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
|
0 |
- 1 |
0 |
0 |
D a G a H 1 = 0 , A " D . H + K " D . H 2 - H 1 = 0 ,
D a L a H 1 = 0 (3)
L 3
или в 11-мерном виде
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
- 1 |
0 |
0 |
0 |
|
0 |
0 |
- 1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
( D a Г a - P )Ф = 0 ,
где
Ф = ( H,H 1 ,H 2 ) t ,
/ 0 Ga 0 \ /0 00
Г a = A a 0 K a , P = 0 14 x 4 0
0 La 0 0 00
G 0 = (1000) , G 1 = (0 - 100) ,
G2 = (00 - 10), G3 = (000 - 1), A0 = (1,0, 0, 0)t, A1 = (0, 1,0, 0)t, A2 = (0, 0, 1,0)t, A3 = (0, 0, 0, 1)t, / 0 0 0 0 0 0\ tv- 0 I — 1 0 0 0 00
K = I 0 -1 0 0 00
\ 0 0 -1 0 00/
/ -1 0 0 0 00
I _ 0 0 0 0 00
K = I 0 0 0 0 0 1 I
\ 0 0 0 0 - 10/
/0 -1 0 0 00 r,2 0 0 0 0 0 -1
К2 = II
K I 0 0 0 0 00
\0 0 0 1 00 /
/0 0 -1 0 00
3 _ 0 0 0 0 10
K = I 0 0 0 -1 0 0 I
00 0 000
/0 1 0 0\ 0010 0 0 0 01
L = 0 0 0 0
I0 0 00
/-1 0 00
0 0 00
1_ 0 0 00
L = 0 0 0 0
I 0 0 0
\ 0 0 10 /
Здесь и далее t обозначает транспонирование.
Уравнение (4) обобщается с использованием тетрадного формализма на случай римановой геометрии пространства–времени (в том числе и на использование любых криволинейных координат в пространстве Минковского) в соответствии со стандартной методикой [6]. Для этого при заданной метрике дав(x) нужно выбрать некоторую тетраду dS2 = дав (x)dxadxe , дав (X) ^ e(a)а (x) , (5)
тогда уравнение (4) должно записываться в пространстве (5) так:
[г а ( X ) ^ + S а ( X )) - P]
Ф( x ) = 0 .
Локальные матрицы Г а ( x ) определяются с использованием тетрады
Г а ( x ) = e Хо ) ( x )Г a =
/ 0 -Gaea)) 0
= A aea)) 0 Kaea)) .(7)
\ 0 Laeao.) 0/
Связность S а ( x ) задается соотношениями
/0 00
Jab = 0 Jab 0
0 0
S а ( x ) = 2 J ab e во ) ( x ) e ( b ) в ; а ( x ) =
/0 00
= 0 (Si) а 0 ,(8)
\ 0 0 (S 2 ) а)
где
S 1 ( x ) = 2 J ob) e во ) ( x ) e ( b ) в ; а ( x ) ,
S2(x ) = 2 J(ab) e O) )(x ) e ( b) в; а (x ) , а Jab) и Jab обозначают генераторы соответственно для вектора Фk(x) и антисимметричного тензора Фmn(x). Уравнение (6) записывается короче с использованием коэффициентов вращения Риччи:
Г c (e а- ) ^+2 J "b i.^ - P ] Ф( x )=о ,
Y [ ab ] c Y [ ba ] c e ( b ) p ; ст e ( a ) e ( c ) • (9)
—ikh 1 —
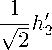
1. Цилиндрические координаты, разделение переменных
2 m
2 - 2 r
h 2 — 0;
Будем рассматривать уравнение (9) в цилиндрических координатах ( r, ф, z ) • В работе [9] после разделения переменных была получена система уравнений по переменной r для массивной частицы Штюкельберга в магнитном поле (аналогичный анализ в кулоновском поле был сделан в работе [10]). В статье [9] использовалась следующая подстановка для волновой функции в циклическом базисе (в котором генераторы J 1 12 , J 2,2 диагональны):
переменные E 1 , 2 , 3 , B 1 , 2 , 3 относятся к шести компонентам антисимметричного тензора; h, h 0 , 1 , 2 , 3 относятся к скаляру и 4-вектору. Размерности этих компонент подчиняются правилу
[ h ] — 1 , [ E i ] — 1 , [ B i ] — 1 ,
[ h 0 ] , [ h 1 ] , [ h 2 ] , [ h 3 ] — ^L • (13)
Ф — , i "e im^ e ik^ ( h, H 1 ,H 2 ) t , H — h ( r ) ,
H 1 = ( h o ( r ) ,h 1 ( r ) ,h 2 ( r ) ,h з ( r )) t ,
H 2 = ( E i ( r ) ,B i ( r )) t .
Из этой системы уравнений, учитывая отсутствие магнитного поля и ограничения, связанные с безмассовостью частицы, получаем следующие 11 уравнений:
—ieh 0 — ikh 2 + — = h '1
2 m — 2
_
х /2 h 3
_
_
2^2 r
h 1
_
2 m + 2
--—— h 3 — 0;
2^2 r
-ieh — ikE2 + EE', x/2 1
2 m — 2
-= E х/2 3
Х h
2 m
+ —^B 2 2^2 r
_
2X 2 r
E 1
_
|
Введем сокращающие обозначения |
|
1 / d m\ 1 / d m\ m —2 \dr r / ’ m —2 \dr r ) , |
|
1 / d m + 1 \ |
|
a m +1 — V2 U ' r ) ’ |
|
1 / d m + 1 \ b m +1 — V2 [dr r ), |
|
1 / d m — 1\ |
|
a m_ 1 — V2 \dr + r ) ’ |
|
b m_ 1 — -p ( T - m—1 ) ’ (14) 2 dr r |
|
тогда система уравнений примет вид |
—ieh 0 — ikh 2 + b m _ 1 h 1 — a m +1 h 3 — 0; (15)
2 m - _.
2 - 2 r E 3 h 0 ’
m , 1 „, h +^B2+
V2 r \2 2
ikB 3 + ieE 1 = h 1 ,
ikh + ieE2 — 1 B '
V2 1
2 m + 2
B
2V2 r
1 B ‘ + x/2 3
2 m — 2
2^2 r
B 3 — h 2 ,
_
— ieh — ikE 2 + b m- 1 E 1 — a m +1 E 3 — h 0 ,
—a m h + a m +1 B 2 — ikB 3 + ieE 1 — h 1 ,
ikh + ieE 2 — a m +1 B 1 — b m _ 1 B 3 = h 2 ,
b m h + b m B 2 + ikB 1 + ieE 3 — h 3 ; (16)
a m h 0 — ieh 1 — 0 , —ikh 0 — ieh 2 — 0
- h 1
-12 h'
2 m
2^2 r
m , 1 „, h +^B2 —
V2 r \ 2 2
B 2 + ikB 1 + ieE 3 — h 3 ;
х /2 h 0 +
2 m
2V2 r
h o
_
ieh 1 — 0 ,
—ikh 0 — ieh 2 = 0 ,
х /2 h 0 +
2 m
—h 0 2^2 r
ieh 3 — 0 ,
_
_
х /2 h 2 +
2 m —
2^2 r
2 m
2^2 r
h 2 + ikh 3 — 0 ,
2 / , 2 m + 2
— hi +-- hh+ +-- ——h 3 — 0 ,
• \2 3 2^2 r
—b m h 0 — ieh 3 = 0 , —b m h 2 + ikh 3 = 0 , b m- 1 h 1 + a m +1 h 3 — 0 , —ikh 1 — a m h 2 — 0 • (17)
Дальше будем использовать метод Федорова–Гронского [11]. Для этого введем оператор третьей проекции спина Y — —iJ 12 (он относится к циклическому базису). Убеждаемся, что эта 11-мерная матрица удовлетворяет минимальному уравнению Y ( Y — 1)( Y +1) — 0 . Оно позволяет ввести три проективных оператора с необходимыми свойствами
P 1 — 2 Y ( Y — 1) , P 2 — 2 Y ( Y + 1) , P 3 — 1 — Y 2 ;
P 1 2 — P 1 , P 2 2 — P 2 , P 3 2 — P 3 , P 1 + P 2 + P 3 — 1 • (18)
Соответственно, полную волновую функцию можно разложить в сумму трех частей ф — Ф1 + Ф2 + Ф3 , Фст — Рст Ф, СТ — 1,2, 3•
|
Получаем явный вид проективных операторов |
||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
P 1 |
= |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
, |
||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|||||||||
|
/ 0 0 |
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
0 0 |
|||||||||
|
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||||
|
0 |
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
0 |
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
0 |
0 |
00 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
P 2 = |
0 |
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||
|
0 |
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
0 |
0 |
00 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|||||||||
|
0 |
0 |
00 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|||||||||
|
0 |
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
)/ |
|||||||||
|
1 |
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
° \ 0 |
|||||||||
|
0 |
1 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||
|
0 |
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
° |
|||||||||
|
0 |
0 |
01 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
0 |
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
P 3 = |
0 |
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
° |
||||||||
|
0 |
0 |
00 |
0 |
0 |
1 |
0 |
0 |
0 |
° |
|||||||||
|
0 |
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||
|
0 |
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
° |
|||||||||
|
0 |
0 |
00 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|||||||||
|
0 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
)/ |
|||||||||
Затем находим структуру проективных составляющих полной волновой функции (учитываем, что в соответствии с методом Федорова–Гронского каждая составляющая должна определяться только одной функцией от переменной r ):
Ф 1 ( r ) = (0 , 0 , h 1 , 0 , 0 , E 1 , 0 , 0 , 0 , 0 , B 3 ) t f 1 ( r ) ,
Ф 2 ( r ) = (0 , 0 , 0 , 0 ,h 3 , 0 , 0 , E 3 ,B 1 , 0 , 0) t f 2 ( r ) ,
Ф з ( r ) = ( h, h 0 , 0 , h 2 , 0 , 0 , E 2 , 0 , 0 , B 2 , 0) t f з ( r ) . (19)
Действуя проективными операторами на систему уравнений (15)–(17), получаем три подсистемы
P 1 : - a m h + a m B 2 - ikB 3 + imE 1 = h 1 ,
amh0 — imh 1 = 0, —ikh 1 — amh2 = 0;
P 2 : b m h + b m B 2 + ikB 1 + imE 3 = h 3 , - b m h 0 - imh 3 = 0 , -b m h 2 + ikh 3 = 0;
P 3 : — imh 0 — ikh 2 + b m- 1 h 1 — a m +1 h 3 = 0 ,
-
— imh — ikE 2 + b m- 1 E 1 — a m +1 E 3 = h 0 , ikh + imE 2 — a m +1 B 1 — b m- 1 B 3 = h 2 , — ikh 0 — imh 2 = 0 , b m - 1 h 1 + a m +1 h 3 = 0 .
Накладываем условия Федорова–Гронского (эти условия позволяют преобразовать дифференциальные уравнения в алгебраические):
P 1
-
—a m f э ( r ) h + a m f 3 ( r ) B 2 — ikf 1 ( r ) B 3 +
+ imf 1 ( r ) E 1 = f 1 ( r ) h 1 ^ a m f 3 = C 1 f 1 , a m f 3 ( r ) h 0 — imf 1 ( r ) h 1 = 0 ^ a m f 3 = C 1 f 1 , —ikf 1 ( r ) h 1 — a m f э ( r ) h 2 = 0 ^ a m f 3 = C 1 f 1 ;
P 2
b m f 3 ( r ) h + b m f 3 ( r ) B 2 + ikf 2 ( r ) B 1 +
+ imf 2 ( r ) E 3 = f 2 ( r ) h 3 ^ b m f 3 = C 2 f 2 ,
—b m f 3 ( r ) h 0 — imf 2 ( r ) h 3 = 0 ^ b m f 3 = C 2 f 2 , — b m f 3 ( r ) h 2 + ikf 2 ( r ) h 3 = 0 ^ b m f 3 = C 2 f 2 ;
P 3
-
— imf 3 ( r ) h 0 — ikf 3 ( r ) h 2 + b m- 1 f 1 ( r ) h 1 —
-
— b m- 1 f 1 ( r ) h 3 = 0 ^ b m- 1 f 1 = C 3 f 3 ,
-
— imf 3 ( r ) h — ikf 3 ( r ) E 2 + b m- 1 f 1 ( r ) E 1 —
-
— a m +1 f 2 ( r ) E 3 = f 3 ( r ) h 0 ^
^ bm-1 f1 = C3 f3, am +1 f2 = C4 f3, ikf3( r) h + imf3( r) E 2 — am+1 f2( r) B1 —
-
—b m- 1 f 1 ( r ) B 3 = f 3 ( r ) h 2 ^
^ b m- 1 f 1 = C 3 f 3 , a m +1 f 2 = C 4 f 3 ,
—ikf3( r) h 0 — imf3( r) h 2 = 0, bm-1f1( r) h 1 + am +1 f 2 (r) h 3 = 0 ^
^ b m- 1 f 1 = C 3 f 3 , a m +1 f 2 = C 4 f 3 .
С учетом наложенных связей получаем алгебраическую систему уравнений
-
— C 1 h + C 1 B 2 — ikB 3 + imE 1 = h 1 ,
C1h0 — imh1 = 0, —ikh1 — C1h2 = 0,
C 2 h + C 2 B 2 + ikB 1 + imE 3 = h 3 ,
-
— C 2 h 0 — imh 3 = 0 , —C 2 h 2 + ikh 3 = 0 , —imh 0 — ikh 2 + C 3 h 1 — C 3 h 3 = 0 , —imh — ikE 2 + C 3 E 1 — C 4 E 3 = 0 , ikh + imE 2 — C 4 B 1 — C 3 B 3 = h 2 ,
-
— ikh 0 — imh 2 = 0 , C 3 h 1 + C 4 h 3 = 0 . (20)
Соберем вместе дифференциальные условия связи bm-1f1(r) = C3f3(r), amf3(r) = C1f1 (r), am+1f2(r) = C4f3(r), bmf3(r) = C2f2(r). (21)
Из (21) следуют уравнения второго порядка для отдельных функций bm-1 amf3 = C1C3 f3, ambm-1 f 1 = C1C3 f1, am+1bmf3 = C2C4f3, bmam+1f2 = C2C4f2. (22)
Параметры в каждой паре могут быть выбраны одинаковыми: C3 = C 1, C4 = C2. При этом условия связи и уравнения принимают вид bm-1 f 1( r ) = C1 f3 , amf3 = C1 f1, am +1 f2( r ) = C2 f3 , bmf3 = C2 f2!
[ b m- 1 a m — C 2 ] f 3 = 0 , [ a m b m- 1 - C 2 ] f 1 = 0 ,
[ a m +1 b m — C 2 ] f 3 = 0 , [ b m a m +1 - C 2 ] f 2 = 0 • (23)
С учетом явного вида (14) операторов первого порядка полученные четыре уравнения записываются так:
|
d 2 |
1 d m 2 |
|
+---- т - 2 C 2 |
|
|
dr 2 |
r dr r 2 1 |
f 3 = 0 ,
|
. dr 2 + |
1 d r dr |
- |
( m - 1) 2 r 2 |
- 2 C 1 2 |
f 1 = 0 , |
|
|
Г d 2 dr 2 |
1 ""1-- r |
d dr |
9 m 2 - r 2 - |
2 C 2 2 f 3 |
= 0 , |
|
|
d 2 |
1 d |
( m + 1) 2 |
- 2 C 2 2 |
f 2 = 0 . |
||
|
- |
||||||
|
dr 2 |
r dr |
r 2 |
Очевидно, должно выполняться условие 2 C 22 = 2 C 2 = C 2 , т. е. имеем три уравнения:
/ d2 1 d dr2 r dr
-
m2 r2
- C 2) f 3 = 0 ,
|
(dr 2 + |
1 d r dr |
- (m-. - C 2) f 1 = 0 , |
|
|
( d 2 1 dr 2 r |
d - dr |
< m^ - C 2 ) f 2 = 0 . |
(24) |
Напомним, что в теории обычной безмассовой векторной частицы также возникает уравнение вида (24):
(
d 2 1 d 2
dr 2 r dr
- k 2
-
2) f =" ■
z = Vm2 - k2r, f (z) = J±m(Z).(25)
Следовательно, в уравнениях (24) надо полагать
-C2 = m2 - k2 ^ C = i^m2 - k2.(26)
В новой переменной z = -iCr = Vm 2 - k 2 r уравнения (24) принимают бесселевский вид:
d2 1 dm
(dz ? + Zdz +1 - ^2) f 3 = 0 ' f 3 = J ±m ( z ’ '
-
(£ +1 d +1 - m - ! : ) f , = 0 ,
dz2 z dzz
-
(# +i d +1 - . ) f 2 = o ,
-
2. Анализ алгебраической системы
dz2 z dzz f 1 = J± (m-1)( z ) , f2 = J± (m +1)( z ) .(27)
Напомним равенства C 1 = C 2 = C 3 = C 4 = C/ V2 и обратимся к алгебраической системе уравнений
-imh о - ikh 2 + C/^2h 1 - C/^2h 3 = 0 ,
-imh - ikE 2 + C/^2E 1 - C/^2E 3 = h 0 ,
-C/^2h + C/V 2 B 2 - ikB 3 + imE 1 = h 1 , ikh + imE 2 - C/V 2 B 1 - C/V 2 B 3 = h 2 , C/V 2 h + C/V 2 B 2 + ikB 1 + imE 3 = h 3 ,
C/\p2h 0 - imh 1 = 0 , -ikh 0 - imh 2 = 0 ,
-C/V 2 h 0 - imh 3 = 0 , -C/^2h 2 + imh 3 = 0 , C/V 2 h 1 + C/V 2 h 3 = 0 , -ikh 1 - C/V 2 h 2 = 0 . (28)
Ее можно записать в матричной форме A 11 х цФ = 0
|
0 |
- im |
C √ 2 |
- ik |
C 2 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
- im |
- 1 |
0 |
0 |
0 |
C - 2 |
- ik |
C - 2 |
0 |
0 |
0 |
||
|
C 2 |
0 |
- 1 |
0 |
0 |
im |
0 |
0 |
0 |
C √ 2 |
- ik |
||
|
ik |
0 |
0 |
- 1 |
0 |
0 |
im |
0 |
C 2 |
0 |
C x/2 |
||
|
C √ 2 |
0 |
0 |
0 |
- 1 |
0 |
0 |
im |
ik |
C √ 2 |
0 |
||
|
A 11 х 11 = |
0 |
C √ 2 |
- im |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
- ik |
0 |
- im |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
0 |
C - 2 |
0 |
0 |
- im |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
0 |
0 |
0 |
C - 2 |
ik |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
0 |
0 |
C √ 2 |
0 |
C √ 2 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
1 |
0 |
0 |
- ik |
C 2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Ф = |
( h, h 1 , h 2 , h 3 , E 1 , E 2 , E 3 , B 1 , B 2 , B 3 ) t . |
|||||||||||
Убеждаемся, что определитель этой матрицы обращается тождественно в нуль при любом выборе параметра C . Ранг матрицы равен восьми. Удаление строк с номерами 9-11 приводит к матрице A 8 х 11 нового размера с тем же
рангом. При C = iVm 2 - k 2 ранг матрицы A 8 х 11 равен шести. Ранг не изменится, если убрать строки 1 и 8 . В результате приходим к шести независимым уравнениям
\
|
- im |
- 1 |
0 |
0 |
0 |
C √ 2 |
- ik |
C 2 |
0 |
0 |
0 |
\ |
|
C 2 |
0 |
- 1 |
0 |
0 |
im |
0 |
0 |
0 |
C √ 2 |
- ik |
|
|
ik |
0 |
0 |
- 1 |
0 |
0 |
im |
0 |
C 2 |
0 |
C 2 |
|
|
C √ 2 |
0 |
0 |
0 |
- 1 |
0 |
0 |
im |
ik |
C √ 2 |
0 |
|
|
0 |
C √ 2 |
- im |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
- ik |
0 |
- im |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
X |
( h, h 0 ,h 1 , h 2 , h 3 , E 1 ,E 2 ,E 3 , B 1 ,B 2 ,B 3 ) ) |
— 0 . |
|||||||||
-
X
Переносим вправо столбцы, отвечающие переменным
h, E 3 , B 1 , B 2 , B 3 , и приходим к неоднородной системе
уравнений с пятью свободными параметрами
h 3
E 1
h 0 h 1
^ —I'm,
V ,ik, VL, 0, 0
)
в
(
в
C
t
E 3
E 2
t
h-
в
в
в
C ,ik, 0 ’ 0)
t
B 1
в
в
C
C
)
t
B 2
в
в
^0,—ik,
в
C
t
B3.
В результате находим пять линейно независимых решений:
h 0
h 1
в
—im \ i m2-k2
h 2
ik
h 3
E 1
E 2
\
i m 2 -k 2
h,
h 0 h 1
в
i√ 2 m 2
m 2 -k 2
-im
h 2
h 3
E 1
E 2
i 2 km
m 2 -k 2
im
в
√ 2 k
E3,
h 0 h 1
h 2
h 3
E 1
E 2
h 0
h 1
h 2
h 3
E 1
E 2
i 2 km m 2 -k 2
-ik
i√ 2 k 2
m 2 -k 2
ik
k 2
k
m
+ m 2
\ V 2 m V m 2 -k 2 /
\
-im i m2-k2
ik
i m 2 -k 2
в
m k
m
B1,
B2,
0,0,0,0 ,kvm
m
в
k2
)
t
B3.
Представляем найденные решения в 11-мерной форме:
(
1, —im,
в
i m2
в
k2
, ik,
i m2
в
k2
( iV2 m12
\ ’ Vm2
в
Vm2
в
-im,
i Vm km
Vm 2
в
k2
, im,
в
k2
( i 72 km
Vm2
в
k2
-ik,
V k12
m2
в
k2
, ik,
в
k
m
,
k2
2m mVm 2
0, -im,
в
('
в
m
в
k2
i m2
в
в
k2
, ik,
i m2
в
k2
,
-,-, 0,0, 1,0
m
m
Известия Коми научного центра Уральского отделения Российской академии наук № 4 (62), 2023
Серия «Физико-математические науки»
в
k2
Vmm
При подстановке их в исходную систему (28) все пять решений дают нули. Следует учитывать, что эти решения найдены с точностью до произвольных множителей.
Заключение
Уравнение для безмассовой частицы Штюкельберга решено в цилиндрических координатах. Полевая функция состоит из скаляра, 4-вектора и антисимметричного тензора. Физически наблюдаемыми величинами являются скаляр (переменная h ) и 4-вектор (переменные h 0 , h 1 , h 2 , h 3 ); физически ненаблюдаемые переменные — компоненты антисимметричного тензора (переменные E i , B i ). Найдены пять линейно независимых решений. При этом свободными параметрами являются h , E 3 , B 1 , B 2 , B 3 .
Список литературы Безмассовая частица Штюкельберга, решения с цилиндрической симметрией
- Duffin, R.I. On the characteristic matrices of the covariant systems / R.I. Duffin // Phys. Rev. – 1938. – Vol. 54, № 12. – P. 1114–1117.
- Kemer, N. The particle aspect of meson theory / N. Kemmer // Proc. Roy. Soc. London. A. – 1939. - Vol. 173. – P. 91–116.
- Огивецкий, В.И. Нотоф и его возможные взаимодействия / В.И. Огивецкий, И.В. Полубаринов // Ядерная физика. - 1966. - Т. 4, вып. 1. – С. 216–223.
- Stueckelberg, E.C.G. Die Wechselwirkungskräfte in der Elektrodynamik und in der Feldtheorie der Kernkräfte (Teil II und III) / E.C.G. Stueckelberg // Helv. Phys. Acta. – 1938. – Vol. 11. – P. 299–312, 312–328.
- Ruegg, H. The Stueckelberg field / H. Ruegg, M. Ruiz-Altabal // Int. J. Mod. Phys. A. – 2004. – Vol. 119. – P. 3265–3348.
- Редьков, В.М. Поля частиц в римановом пространстве и группа Лоренца / В.М. Редьков. – Минск: Беларус. навука, 2009. – 486 с.
- Плетюхов, В.А. Релятивистские волновые уравнения и внутренние степени свободы / В.А. Плетюхов, В.М. Редьков, В.И. Стражев. – Минск: Беларус. навука, 2015. – 328 с.
- Elementary particles with internal structure in external fields. Vol. I, II / V.V. Kisel [et al.]. - New York: Nova Science Publishers Inc., 2018.
- Овсиюк, E.M. Частица Штюкельберга во внешнем магнитном поле. Метод проективных операторов / E.M. Овсиюк [и др.] // Известия Коми научного центра Уральского отделения Российской академии наук. Серия «Физико-математические науки». – 2022. – № 5 (57). – С. 69–78.
- Stuckelberg particle in the Coulomb field, non-relativistic approximation, wave functions and spectra / E.M. Ovsiyuk [et al.] // Nonlinear Phenomena in Complex Systems. – 2022. – Vol. 25, № 4. – P. 387–404.
- Гронский, В.К. Магнитные свойства частицы со спином 3/2. / В.К. Гронский, Ф.И. Федоров // Доклады Национальной Академии наук Беларуси. – 1960. – Т. 4, № 7. – С. 278–283.


