Безопасность в сфере конфиденциальной информации и закон формирования простых чисел

Н ачнем с того, что теория шифрования с использованием открытого ключа была создана в 1976 г. У. Диффи и М. Хеллманом [1] и впервые реализована в 1977 г. в RSA-алгоритме Р. Райвестом, Э. Шамиром и Л. Эдлманом. Она основывалась на так называемых односторонних функциях: по некоторому x легко вычислить его функцию f(x) , но, зная f(x) , трудно вычислить х .

Понятно, что в RSA-алгоритме была использована достаточно простая идея - вычислить произведение двух простых чисел легко (прямая задача), а разложение полученного в результате этой операции числа на простые множители (обратная задача) достаточно трудоемко. Ибо время вычислений экспоненциально возрастает при увеличении количества битов в полученном открытом ключе.

Именно поэтому компания RSA, основанная вышеперечисленными авторами, до сих пор предлагает желающим различные задачи факторизации представленных ею чисел. В частности, задача разложения на множители числа, состоящего из 155 разрядов, требует более 35 лет непрерывной работы самого современного компьютера.

Несмотря на то, что для ее решения реально потребовалось около 4 месяцев благодаря распределенным вычислениям в компьютерной сети, алгоритмы компании пользуются успехом, несмотря на увеличивающуюся вычислительную мощность компьютерных систем.

А если знать закономерности формирования простых чи- сел, как бы изменились алгоритмы шифрования, подобные RSA? А как бы изменились подходы к дешифрованию?

И второй вопрос. В каком направлении пошла бы разработка новых современных алгоритмов шифрования со знанием законов формирования натурального ряда? Квантовая криптография – как соединение физики и математики, или иная - невероятная еще вчера идея?..

Простые числа и алгоритм RSA

В мире исследований простых чисел со все возрастающими временными интервалами делаются очередные шумные открытия – находится новое гигантское простое число. С помощью сотен тысяч компьютеров, объединенных в рамках проекта Great Internet Mersenne Prime Search (GIMPS), счастливчики натыкаются на «числовые жемчужины» – очередные простые числа Мерсенна - 2^P-1 , где p – также простое число. Проверка на простоту усложняется с ростом величины числа и уже давно вышла за пределы физических возможностей человека: выполнить проверку простоты числа длиною в миллионы цифр можно лишь с помощью компьютеров, да и им потребуются на это годы.

Что дает открытие нового числа Мерсенна человечеству?

Увы, ничего значительного: какой-то теоретической и практической отдачи от такого открытия не предвидится. К пониманию законов распределения простых чисел в натуральном ряду эти открытия науку также не приближают.

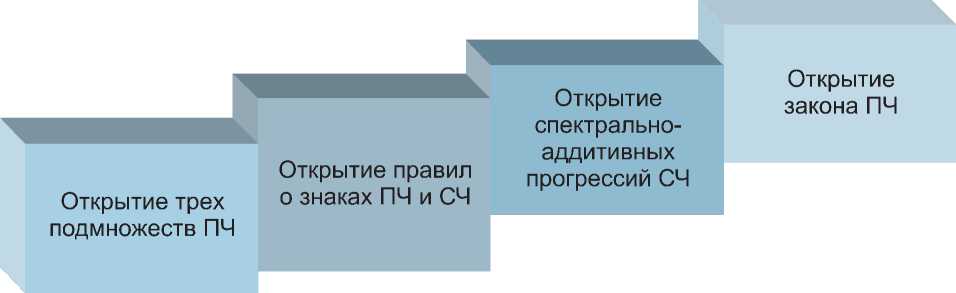
Рис. 1. Ступени постижения закономерностей формирования ПЧ и натурального ряда

Мы же сегодня публикуем самое большое известное простое число. Оно значительно больше последнего открытого числа Мерсенна и равно - … Впрочем, стоит ли публиковать? Завтра мы опубликуем новое число. А послезавтра – опять новое. И так – каждый день, час, минуту… Можем огромным списком, в том числе включающим новые числа Мерсенна.

У компании Electronic Frontier Foundation (EFF), то есть у фонда, материально поддерживающего идею поиска самых больших чисел, средств на нас явно не хватит. Поэтому ждем последнего приза в 100 тысяч долларов.

А не хватит средств потому, что в России открыт закон формирования простых чисел [2]. И это кардинально меняет картину в мире исследований простых чисел (в математическом мире простые числа называют Prime Numbers - первые числа), в частности – резко упрощает процедуру проверки чисел на простоту, в том числе и чисел Мерсенна.

Открытие в прикладном смысле особенно отразится на сфере информационной безопасности.

Ученые, работающие в этой сфере, пытаются разработать алгоритмы и вычислительные устройства, способные с высокой скоростью раскладывать большие числа на простые множители. Ведь, как известно, именно принцип вычислительной трудности факторизации (разложения на множители) больших чисел положен в основу многих современных криптографических алгоритмов. Наиболее распространенным алгоритмом в области обеспечения защиты конфиденциальной информации является алгоритм RSA.

Дадим оценку степени сложности вскрытия RSA.

Так, ключи длиной 256 бит легко факторизуются обычными программистами. Ключи в 384 бита могут быть вскрыты исследовательской группой крупного университета или компании. Далее - 512-битные ключи находятся в пределах досягаемости спецслужб крупных государств. Ключи длиной в 1024 бит могли считаться безопасными до тех пор, пока не будет существенного прогресса в алгоритме факторизации либо открытия закона формирования простых чисел.

Ключи длиной в 2048 бит в большинстве считаются надежными на десятилетия. А напрасно так считают. Мир простых чисел, а точнее мир их понимания изменился. Во- первых, найден алгоритм формирования простых чисел от 1 до бесконечности. И это – изменение мировоззрения, означающее, что не нужно находить простые числа путем использования различных, подчас довольно сложных методов. Во-вторых, изменяются процедуры проверки найденного числа на простоту.

Да, пока не найдены алгоритмы факторизации числа. Однако резко (на порядки) упрощаются алгоритмы нахождения простых чисел, составляющих так называемые «полупрос-тые» числа (которые делятся только на себя, единицу и два других простых числа).

В целом, если сделать относительные оценки, «расколоть» ключи RSA становится возможным не более, чем за 100 шагов, по сравнению с прежними 1 млн. И это – верхний предел. Возможно и быстрее.

А теперь - о главном.

Из истории проблемы

Со времен древнегреческой цивилизации лучшие умы человечества пытались познать закономерность, согласно которой формируются простые числа (ПЧ). До наших времен дошли две жемчужины математического мышления древних: «решето просеивания» ПЧ Эратосфена и доказательство Евклида бесконечного числа ПЧ.

За прошедшие тысячелетия были успехи на пути познания указанной закономерности, но они не стали кардинальными. В частности, Л. Эйлеру, а также Ю. Матиясевичу удалось составить алгебраические уравнения, с помощью которых в ограниченном интервале натурального ряда получались только простые числа.

Усилиями Гаусса, Чебышева, Адамара, Ла Валле Пуссена и Римана сформирован «Асимптотический закон распределения простых чисел». Но с помощью этого закона, к сожалению, нельзя точно определить ни количество ПЧ в определенном интервале, ни ПЧ по индексу, ни индекс ПЧ.

В чем же первопричина непостижимости таких непростых «простых» и крайне важных для науки и практики чисел? Давайте попробуем разобраться в этом вопросе, предложив описание закономерностей формирования ПЧ и всего натурального ряда.

В настоящее время, в сложившейся парадигме современной математики, определяются следующие натуральные числа: четные {2n} и нечетные {2n-1} , где n = 1, 2, 3, 4 …; простые {1, 2, 3, 5, 7…} и составные {4, 6, 9, 10,…} . Такая неоднозначная классификация, когда одно и то же число может быть отнесено к разным классам (2 – одновременно число и простое, и четное, 9 – одновременно число нечетное и составное, а 5 - нечетное и простое), вызвана тем обстоятельством, что за всю историю математики поиски элементарных формул, дающих только ПЧ (без ограничения диапазона вычислений), оказались тщетными.

Ступени постижения закономерностей

На пути постижения авторами закономерностей формирования натурального ряда чисел и его составной части - ПЧ -оказалось четыре ступени, отображенные на рис. 1 .

Постижению закономерностей формирования натурального ряда и ПЧ на первой ступени послужило осмысление способов образования ПЧ. На этой ступени были определены три качественно отличные подмножества ПЧ: подмножество фундаментальных³ ПЧ {2, 3} ; подмножество отрицательных ПЧ ^–Р = { 5, 11, 17, …} , образующихся путем вычитания 1 от чисел, кратных 6; подмножество положительных ПЧ ⁺Р = { 7, 13, 19, …} , образующихся путем прибавления 1 к числам, кратным 6.

На второй ступени определение трех качественно отличных подмножеств ПЧ позволило сформулировать правила о знаках простых и составных чисел (СЧ).

На третьей ступени было определено, что последовательность 6n-1 содержит все отрицательные ПЧ и СЧ, а 6n+1 -все положительные ПЧ и СЧ.

Вычитая из этих двух последовательностей соответственно все отрицательные СЧ и все положительные СЧ, получаем все ПЧ, кроме фундаментальных . Так была преодолена четвертая ступень познания и открыта закономерность формирования ПЧ.

Пройдем все эти ступени вместе.

Для начала определим множества всех отрицательных ПЧ как ^_Р , отрицательных CЧ как ^_C , положительных ПЧ как ⁺Р и положительных CЧ как ⁺С .

Открытие законов – это просто

Для начала вспомним знаменитую теорему Евклида: «Простых чисел существует больше их любого указанного числа». Теорему Евклид доказал красиво и элегантно, использовав для образования ПЧ следующее соотношение:

р₁ × р₂ × … × р_n + 1 = ⁺М

Однако у одного из авторов данной статьи - В.П. Хренова -еще в 2002 г. возник вопрос о полноте представления всех ПЧ соотношением {р_n!+1} ( назовем р_n! факториалом ПЧ). Существуют ли ПЧ, не представленные данным соотношением? И он показал, да, существуют! И составил соотношение, мимо которого на протяжении столетий проходили математики:

р 1 × р 2 × … × р n – 1 = ^-М

А далее – проблема. Данные способы образования чисел р_n! ± 1 дают не только положительные и отрицательные ПЧ, но и положительные и отрицательные СЧ. Кроме того, не все положительные и отрицательные ПЧ и СЧ образуются с помощью соотношения р_n! ± 1 . Есть и пропуски, и весьма значительные. Как же получить все до одного ПЧ и СЧ?

Собравшись вместе, В.А. Минаев и В.П. Хренов доказали теорему, содержание которой сводится к следующему: «Последовательность 6n–1 содержит все отрицательные ПЧ и СЧ, а последовательность 6n+1 , где n = 1, 2, 3 …, содержит все положительные ПЧ и СЧ».

А потом они доказали теорему о знаках ПЧ и СЧ, смысл которой, если говорить просто, заключается в том, что произведение нескольких отрицательных и положительных ПЧ дает положительное СЧ при четном количестве отрицательных ПЧ и отрицательное СЧ при их нечетном количестве.

А что же делать дальше, как отделить простые и составные числа во множествах 6n ± 1 ? И тут осенило В. Хренова. Ну, конечно же, для образования всех составных чисел нужно применить прогрессию (ее автор назвал спектрально-аддитивной), отражающую сущность простых (первых) чисел быть первыми в образуемых ими прогрессиях.

Если говорить на языке математики, то напомним, что арифметическая прогрессия позволяет путем неограниченного сложения выявленную закономерность устремить в бесконечность, а наибольший общий делитель (НОД) позволяет устанавливать свойства целых чисел относительно деления ( умножения ).

Синтез этих двух понятий позволяет получать аддитивные прогрессии. Если в качестве НОД принимать только одно ПЧ р_i , то можно получать аддитивные относительно р_i прогрессии (спектрально-аддитивные прогрессии) . При этом НОД обретает смысл нового математического понятия – наименьшего общего множителя (НОМ) .

Последовательное присоединение к p_i кратного количества этого же p_i образует арифметическую прогрессию с НОМ, равным этому ПЧ:

{p i , (p i + kp i ), (p i + 2kp i ), (p i + 3kp i ),…} =

{p i + p i kn} = p i {1 + kn}                                    (1)

где p_i – какое-либо ПЧ, k – коэффициент кратности, n = 0, 1, 2, 3 …

Для р 1 = 2 имеем 2 С = {2, 2+2×1, 2+2×2, 2+2×3,…} = { 2+2 × n} .

При n = 0 , это фундаментальное ПЧ = 2 , а при n ≥ 1 и k = 1 это все четные числа {4, 6,…} .

Применяя соотношение к фундаментальному ПЧ = 3 , и приняв k = 2 , имеем:

3 С = {3, 3+3×2×1, 3+3×2×2, 3+3×2×3,…} =

{3 + 3×2n}.

При n = 0 , это ПЧ = 3 , а при n ≥ 1 , имеем (по аналогии) все нечетные числа {9, 15, …} .

Применяя соотношение (1) ко всем остальным ПЧ {5, 7, 11,…} , необходимо учитывать правило знаков, которому подчиняются образуемые ими СЧ. Каждое из этих СЧ в зависимости от знаков сомножителей, как уже говорилось, входит либо в 6n-1 , либо в 6n+1 .

А затем был открыт закон формирования составных чисел по формуле piС = piкi + piкjn,                                                (2)

где n = 0, 1, 2, 3,… ; к_i и к j – константы, принимающие следующие значения:

• ■    у фундаментальных ПЧ 1 Р = 1 + 1п при р₀ = 1 , k i = 1 , k j = 1 и n ≤ 2 ;

• ■    у четных (двухкратных) чисел 2 С = 2 + 2п при р 1 = 2 , k_i = 1 и k j = 1 ;

• ■    у нечетных (трехкратных) чисел ₃С = 3 + 3*2n при р₂ = 3, k_i = 1 и k j = 2 ;

• ■    у отрицательных СЧ ^_р1⁷С при k i = ⁺p, (при НОМ = - р, ) или к_i = ^-p_i+1 (при НОМ = ⁺p_i ) и k j = 6 ;

  
  
  

• ■    у положительных СЧ Т._р1⁷С при к = + Pi (при НОМ = + p_f ) или к_i = ^-p_i (при НОМ = ^-p_i ) и k j = 6 .

Этот закон - ядро формирования следующих законов, до авторов не открытых никем! А именно, учитывая закон формирования составных чисел, был сформулирован Закон простых (первых) чисел: « Множество всех первых (простых) чисел состоит из подмножества фундаментальных ПЧ ₁Р, подмножества отрицательных ПЧ ^–P, равного разности между множеством 6n-1 и суммой всех спектрально-аддитивных прогрессий отрицательных СЧ Σ_Pi^-C, и подмножества всех положительных ПЧ ⁺P, равного разности между множеством 6n+1 и суммой всех спектрально-аддитивных прогрессий положительных СЧ Σ _Pi⁺C».

Открытие этого закона позволило только операциями сложения получать все ПЧ и СЧ в заданном диапазоне вычислений и таким образом создать линейный генератор ПЧ подряд. И он был создан и запатентован В. Хреновым [3, 4]. А далее почти очевидное открытие закона формирования структуры натурального ряда: «Натуральный ряд N состоит из:

Ф нуля и единицы;

2 двух фундаментальных ПЧ ( 1 Р = {2, 3});

® отрицательных ПЧ (^-Р)_;

• 4    положительных ПЧ ( + Р);

• 5    четных СЧ ( 2 C, куда входят циклические числа 6 C);

нечетных СЧ (3C)

7 прогрессий отрицательных (L Pi- С) и положительных (Σ Pi ⁺С) СЧ».

Этот закон однозначно расщепляет натуральный ряд на 7 качественно различных множеств подобно призме Френеля, расщепляющей белый свет на 7 цветов радуги.

С открытием закономерностей формирования натурального ряда и ряда ПЧ числовая система Природы обрела кристальную ясность и может положить начало универсальному языку познания – математике Природы (натуральной математике), основанной на парадигме дискретно-непрерывного пространства и закономерностях натурального ряда.

Чтобы говорить с Природой на одном языке, потребуется изучить и развить «азбуку» этого языка. Настоящая статья -только первый шаг к серьезному переосмыслению окружающего нас мира и присущих ему математических и физических закономерностей, а также основам преподавания математики.

Открытые математические закономерности позволяют создать средства защиты информации (СЗИ) нового поколения на одноразовых ключах и одноразовых непериодических гаммах псевдослучайных чисел на конечных автоматах, что до настоящего времени считалось невозможным. Такие СЗИ теоретически будут обладать максимальной надежностью и быстродействием режима online [5].