Безредукторный асинхронный привод в системах низкочастотной виброобработки металлических конструкций

Одним из наиболее эффективных и экономичных способов снижения остаточных механических напряжений в металлических конструкциях и изделиях является применение технологии низкочастотной виброобработки. Она позволяет в ряде случаев не только отказаться от термической обработки изделий, что является достаточно трудоемким, требующим больших энергетических и финансовых ресурсов процессом, но и снизить уровень остаточных сварочных напряжений на 25–50 % в зависимости от различных марок сталей [1–4].

Как правило, существующие для этой цели электромеханические системы должны формировать сложные траектории движения, сочетающие в себе в зависимости от требований технологического процесса вращательную, колебательную и пульсирующую составляющие с регулируемыми параметрами. Конструктивно они выполняются на базе машин постоянного или переменного тока с дополнительными механическими звеньями преобразования параметров движения, что существенно ограничивает их динамические возможности по частоте вибрационной составляющей движения и ее формы, снижая надежность всей системы в целом.

Одним из решений поставленной задачи, позволяющим устранить перечисленные недостатки, может служить построение безредукторного вибрационного электропривода на основе двухфазного асинхронного электродвигателя (АД), работающего непосредственно в режимах колебательного или вращательно-периодического движения за счет фазовой модуляции питающих напряжений или токов [5, 6].

Функциональная схема электропривода

На рис. 1 представлена функциональная схема электропривода, реализующая потенциальный фазовый способ формирования вращательной, колебательной и пульсирующей составляющих закона движения в двухфазном АД.

Она содержит: частотный демодулятор (ЧД), преобразующий частоту питающей сети ю 1 в пропорциональный уровень постоянного напряжения U _в1 ; два сумматора (SM1, SM2); прецизионный регулируемый блок питания постоянного напряжения (ПБП), задающий постоянное напряжение U ^ , пропорциональное частоте колебаний (пульсаций) Q; два преобразователя напряжение-частота (ПНЧ1, ПНЧ2); фазовое звено (ФЗ), сдвигающее по фазе входное напряжение сети на ±90 градусов; электронные ключи (SA1, SA2), определяющие режим работы электропривода; модулятор; выпрямитель и усилитель мощности (УМ).

При формировании колебательного режима работы АД электронные ключи SA1, SA2 находятся в положении 1. При этом обмотка возбуждения асинхронного двигателя (ОВ) запитывается непосредственно от сети напряжением

U р . ⁽ t ) = U_m i ^cos( ® i t + « ), ⁽¹⁾ где U m 1 – амплитуда напряжения источника переменного тока частоты ю 1 ; а - начальная фаза напряжения источника переменного тока.

Блоки ЧД, ПБП и первый сумматор формируют постоянное напряжение, пропорциональное частоте ю 2 , которое преобразуется на выходе ПНЧ в переменное напряжение

Um2( t ) = Um 2sin(®2 t + в), где Um2, Р - амплитуда и начальная фаза выходно-

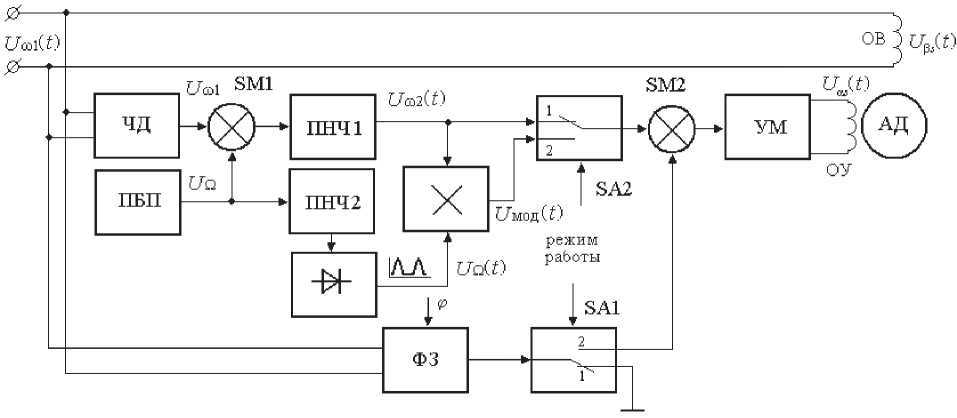
Рис. 1. Функциональная схема электропривода

го напряжения преобразователя напряжение-частота; ® 2 = w 1 + Q.

Благодаря такому подходу, при формировании частоты ю₂ удается избежать влияние девиации частоты колебаний, вызванную нестабильностью частотой сети ю 1 . При этом, точность задания и поддержания частоты колебаний будет определятся только лишь стабильностью прецизионного регулируемого блока питания постоянного напряжения [7].

Усилитель мощности (УМ) усиливает входной сигнал по мощности и запитывает обмотку управления асинхронного двигателя (ОУ). В результате в воздушном зазоре АД формируется колебательное электромагнитное поле [8, 9], для ко- торого закон движения результирующего про- странственного вектора потокосцепления χ0 и его модуль Ys определяются как

X 0 = arg^{[ Y} 5 1 = arctg

^P m 2 sin^ t + Y)

^P m l c^os(® 1 t + 5)

P5 = mod [P^ ] =

V[Pm 1 cos(®1 t + Y)]2 + [Pm2 sin(®2 t + 5)f , где Ymi, Ym2, у , 5 - амплитудные значения и начальные фазы фазных потокосцеплений.

При формировании вращательно-колебательного режима работы электронный ключ SA1 переводится в положение 2. Тогда, сформированное на выходе ПНЧ напряжение поступает на первый вход второго сумматора и складывается в нем с выходным напряжением ФЗ:

U £ = [ U m 2 ^sin(® 2 t ^{+ e} ) ± k l U ml ^sin(® 1 t ^{+ a} ) ] , ⁽²⁾ где k ₁ – коэффициент передачи фазосдвигающего звена (ФЗ).

В результате результирующий пространственный вектор потокосцепления имеет две составляющие: колебательную, от взаимодействия пото-косцеплений, вызванных напряжениями

U m ₁cos( to ₁ 1 + a ) и U m ₂ sin(®₂ 1 + в ), и вращательную, от взаимодействия напряжений

Um 1cos(to11 + a) и ±Um3sin(®11 + a ), где Um3=k1Um1.

В соответствие с законом изменения результирующего вектора потокосцепления

X 0 = arg^ 5 ^] =

= arctg

^P m 2 ^sin⁽to 2 t + Y)

^P m 1 ^coS⁽to 1 t + ⁵⁾

i^ m - tg(® 1 1 + 5);

^P m 1

p 5 = mod [P 5 ] = ([p m1 cos(to1 t + Y)]2 +

⁺ [ ^P m 2 ^sin(® 2 t ^{+ 5)} ± ^P m 3 ^sin(® 1 t ⁺ Y) ] 2

подвижный элемент асинхронного двигателя начинает совершать вращательно-колебательное движение.

На рис. 2 представлены временные диаграммы, полученные при моделировании электропривода, выполненного на базе асинхронного электродвигателя АИР 71А2 в программной среде MATLAB, иллюстрирующие законы изменения электромагнитного момента M _эм( t ), скорости ^ ( t ) и координаты χ( t ) подвижного элемента асинхронного двигателя при колебательном и вращательноколебательном режимах работы за счет фазовой модуляции питающих напряжений.

Вращательно-пульсирующий режим работы привода обеспечивается за счет переключения ключа SA2 в положение 2. При этом осуществляется прерывания напряжения обмотки управления с частотой Q в моменты времени, когда электромагнитный момент, развиваемый АД, переходит через ноль. Последнее достигается за счет преобразования постоянного напряжения U _Q в напряжение переменного тока частоты Q с последующим детектированием его и перемножением на модуляторе с напряжением U _в2 ( t ):

Безредукторный асинхронный привод в системах низкочастотной виброобработки металлических конструкций

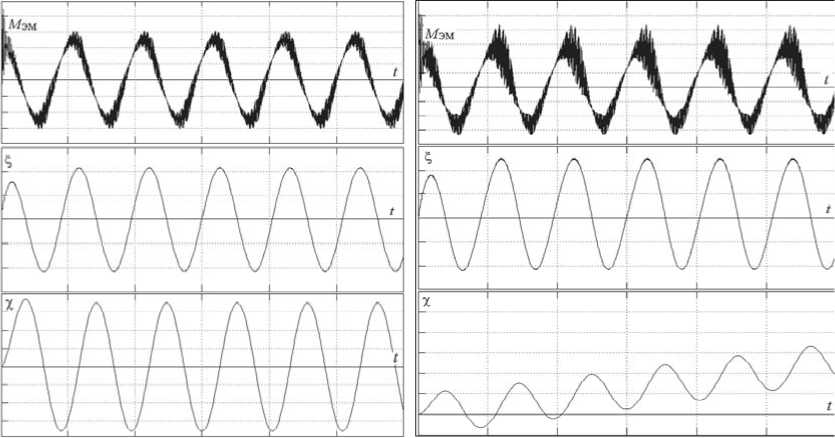
а)                                                               б)

Рис. 2. Выходные характеристики АД при формировании колебательного (а) и вращательноколебательного (б) режимов работы при инерционной нагрузке и запуске на частоту О = 6 рад/с

Uмод (t) - Um О х fl 1        2-Д cos 2iОt  1

х  + -sin О t —У-------M U ( t ), (3)

[ 2 2        n ^(2 i - 1)(2 i + 1)J “ ²

где U m _О - амплитуда напряжения частоты пульсаций.

Оценка выходных параметров электропривода

Оценить скорость вращательной и колебательной (пульсирующей) составляющих закона движения подвижного элемента двигателя для установившегося режима работы можно на основании решения системы дифференциальных уравнений, описывающей электрическое состояние обмоток обобщенной электрической машины с учетом суммарного усилия нагрузки и функций регулирования вида (1)-(3):

и _а, ( t ) = RA_s + L ^{a s}di ²^ + M ^a di ^{a r} ;

aas as      dt dt и ia=r i + LPsdiPs. , Mpdipr .

Ups(t) Rpis+ dt + dt ’ п (n-P ; I La rdar . Ma dias

^U a r ⁽ t ) = R a r i a r ⁺ T ⁺ T-- dt dt

, - ^ ^{( M} p i p s ⁺ L p s i p r ) ^;                             (4)

IT -Ri + LPrdier + M P diPs ,

^U p r ⁽ t ) - R p r i ap ⁺--T--⁺--T-- ⁺ dt dt

• + ^( M a i a s + L a _si a r ) ;

M - k ( M i i_pr - M рТрД^.) -эм q         ^a ^a s I—* ’                    f-’ s '-a r

• ^{- M н} f j ^ ^dt , ^ , d -) ,

где U a s , U в s , U a r , U в r ; i a s , i p s , i a r , i p r - соответственно напряжения и фазные токи в обмотках статора и ротора по осям a и Р; ^ - обобщенная скорость подвижного элемента привода; М _эм и М _н - обобщённые электромагнитное усилие и нагрузка; R a s , R p s , R a r , R p r , L a s , L p s , L a r , L p r , M _a , M p - электрические параметры асинхронного двигателя; k_q - обобщенный силовой коэффициент.

Для этого, исходя из условия, что частота колебательной составляющей закона движения О как минимум на порядок меньше частоты питающей сети ю1, из первых четырех уравнений системы (4) определяются фазные токи и их первые производ- ные по скорости при заторможенном роторе и рассчитываются пусковая и демпфирующая состав- ляющие электромагнитного момента согласно методике [10].

Ограничиваясь линейными слагаемыми по периодической составляющей электромагнитного демпфирования Мдемп, значение вращательной ^вр и колебательной ^кол составляющих скорости элек- тропривода определяются, соответственно, как

^ вр ⁽ t ) ^- :^1sin C У пуск

2 R

d

^ кол ⁽ t ) ^--Г dt

- 2ф - r)- еии— Sin(Yпуск- 2 ф);

2 Mдемп пуск cos(y пуск

^{- r} ) ^{- cos(} т + Y пуск ^{- r} ) ⁺

⁺ .. ^{1    sln}i 7 уск ^{- r} ) ( е ^- M ^{пуск Т -} 1 )

M демп где R - V1 + M^емп ;  r - arctg(1 / Mдемп); т - °t;

ф, У пуск - начальные фазы закона движения подвижного элемента привода и эквивалентного пускового усилия; М _пуск - амплитуда пускового усилия.

Первая гармоническая составляющая амплитуды χ m и начальная фаза колебательной составляющей закона движения электропривода с учетом

нагрузки рассчитываются как

^X m

^

м пуск

О ( R мех - М демп ) V 1 + Z 2 ( « ) ’

^{Ф Y} пуск

- arctg

Z ( О ),

Представленные выражения (5) позволяют определить условия автономности регулирования параметров колебаний по координате, скорости или усилию. Они связывают частоту колебаний О с функциями регулирования. Так, например, при отсутствии позиционной нагрузки С _мех =0, что является наиболее частым случаем работы электропривода, условие автономности амплитуды колебаний при регулировании частоты О можно записать как

где комплексный коэффициент нагрузки

Z ^{( О )} = ( C мех ^— L мех ^О ) / R мех ^О ;

L _мех, R _мех, C _мех – коэффициенты инерционного, демпфирующего и позиционного усилия нагрузки.

Как следует из выражения (5), амплитудночастотные характеристики колебательной составляющей движения привода при малом механическом демпфировании могут иметь при значении позиционной нагрузки С_мех = L_мехО электромеханический резонанс. Однако этот режим допустим только при формировании колебательного движения. При вращательно-колебательном режиме наличие даже незначительного C мех приводит к срыву вращательной составляющей движения и переходу к колебательному режиму работы.

В общем случае регулирование амплитуды может осуществляться за счет изменения амплитуды выходного напряжения U_{m 2} преобразователя напряжение-частота (ПНЧ), воздействуя тем самым на величины М _демп и М _пуск. На рис. 3, а представлены законы регулирования составляющих электромагнитного момента и амплитуды колебательной составляющей движения.

Как видно, они имеют существенно нелинейный характер, вызванный периодичностью коэффициентов модели электрической машины, а также бигармоничностью функций регулирования [11].

Величину вращательной составляющей скорости регулируют за счет изменения величины коэффициента передачи фазового звена (ФЗ), а направление вращения – полярностью его фазового сдвига.

О =

^^^^^^в

⁽ R мех

⁽ R мех

^^^^^^в

^^^^^^в

^М демп ) 2

2 L _мех

^М демп ) ⁴

4 ^L мех

+

м пуск

22 мех ^х m

Рис. 3, б иллюстрирует данные зависимости при различных заданных значениях амплитуды χm.

Установлено, что если необходимо формирователь вращательно-колебательный режим работы электропривода с, так называемой, ползучей скоростью, с помощью ФЗ напряжение на выходе ПНЧ устанавливается согласно выражению

U £ = [ U m 2 sin⁽® 2 t ^{+ в} ) ± ^k 1 U m1 ^cos(® 1 t ^{+ а} ) ] ^.

При этом вращательная составляющая движения подвижного элемента привода будет определяться соотношением амплитуд напряжений U_{m 1} и U_{m 3}. Как показывает практика, такой режим работы является более предпочтительным в электроприводах, предназначенных для виброобработки сварных изделий.

Заключение

Проведенные исследования показали, что использование безредукторного асинхронного электропривода в системах низкочастотной виброобработки металлических конструкций позволяет существенно повысить сопротивления усталости сварных соединений, и тем самым улучшить эксплуатационную надежность сварной конструкции. Разработанный электропривод позволяет форми-

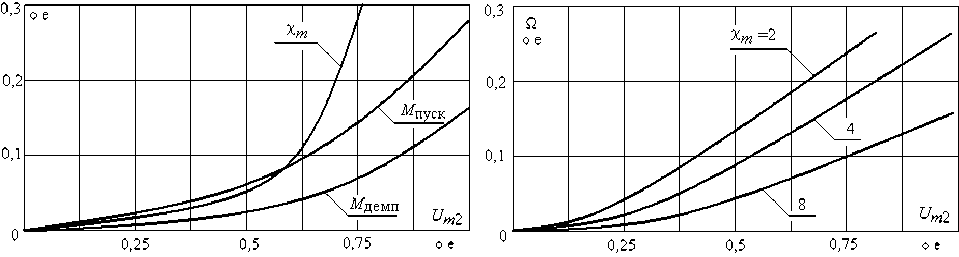
а)

б)

Рис. 3. Законы регулирования пусковой и демпфирующей составляющих электромагнитного момента и амплитуды колебаний (а), условия автономности регулирования амплитуды колебаний (б) при заданных значениях χ _m

Безредукторный асинхронный привод в системах низкочастотной виброобработки металлических конструкций ровать требуемые режимы работы с обеспечением плавного регулирования «на ходу» выходных параметров движения.

Следует отметить, что рассмотренная функциональная схема электропривода и полученные выражения для выходных характеристик справедливы как для двигателей углового, так и линейного движения. Различие состоит лишь в том, что при расчетах системы уравнений (4) силовой коэффициент для угловых колебаний k_q = 1, а для линейных – k q = π/τ p , где τ – полюсное деление, p – число пар полюсов асинхронного двигателя.