Бифуркации на фрактальном строительном рынке

Фрактальная теория и практика развиваются в различных задачах, отражая неоднородность среды (например, [1]). Фрактальные методы анализа уникальности и особенностей исследуемой системы базируются на фрактальной размерности и меры однородности, сложности [2], а также бифуркации (поведения вблизи точек ветвления решений под воздействием малых шумов).

Можно в качестве управляющего параметра отражающего динамику процесса на строительном рынке взять фрактальную

строительный, рынок, волатильность, мо- размерность d [3]. На строительном рынке волатильность всегда наблюдается, поэтому использование параметра d в качестве управляющего оправдано [4].

Если x(t; d) - реактивность строительного рынка на внешнее воздействие, например, кризисные явления, а y(t; d) -капитализация на рынке к моменту времени t, то для х можно согласно теории бифуркаций принять гипотезу кубического закона развития:

a1(d)x(t; d) + a2(t; d)x3(t; d) = A;

для у можно принять аналогичную гипотезу:

b1(d)y(t; d) + b2(t; d)y3(t; d) = В.

Параметры a 1 , b 1 , a₂, b₂ - трендовые, A, В - потоковые, определяющие влияние ресурсных рыночных потоков на динамику или волатильность рынка.

Если принять, отвлекаясь от ситуаций с «пузырями» (например, американских де- ривативов, контрактов типа «фьючерс» или «опцион», известных своей излишней волатильностью), гипотезу квазиравновесия или медленного характера динамических изменений на строительном рынке, то можно записать условия:

х (t; d) « 1, A « 1, у (t; d) « 1, В « 1.

Мы пока не замыкаем систему законов развития х и у, предполагая их относительную расщепляемость. Далее мы рассматриваем реакцию процесса лишь по фрактальной размерности d, т.е. считаем, что x(t; d) = x(d), y(t; d) = y(t), 0 < d < D .

С помощью замен

х = Х. =

У = Yn

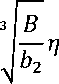
можно уравнения для х, у записать, соответственно, следующими выражениями:

^²- | = Л, 2     ¹

^2—^ = ^, где

Л = м =

Q i ³ j^^ ^, b i

/2 в

Данные уравнения решаются численно или формулой Кардано и имеют нижеследующие вещественные корни:

(

f t =

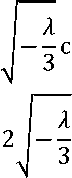
—4!

С +

- 27         \ \

1 4AV1-c)), i = 1, Л < 0,

i = 2, аЛ <

,

P t =

к

2^cos(3dt) cos (-arccos VC + dt), i = 3,4,5.

—i2V

1|n( ⁴V-C+  ⁴ “ vT-C)), i = i, м<0,

i = 2, ам < Hr,

к

2^М cos(3d_t) cos (-arccos VC + d_t), i = 3,4,5.

Здесь параметры задаются в виде:

п           тт          27

^ 3    0,     ^ 4      ^,      ^ 5    ^, ^C ^^ 3 .

Точки бифуркации, соответственно, определяются в виде:

Л(С) =

.(d) —

з|27

J4'

J4

где корни уравнений равны, соответственно:

51 = V2, 2 ^ 1 = V2'

i 52-^ з -  3^2, i ^ 2 = П 3 =    з^,

Возможны скачки в точках Л, р, равные величинам

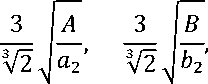
и соответствующие кризисным явлениям на рынке.

Методы и аппарат фрактального анализа успешны при решении задач формирования бифуркационной картины процесса, исследования характеристик (например, в нестабильных зонах). Можно оценить «решения с последствиями» для строи-

тельного рынка, развитие аномалий с небольшими вычислительными сложностями алгоритмического характера.

Исследование фрактальности строительного рынка можно вести на основе R/S-анализа, индекса Херста Н, фрактальной размерности d и толщины хвоста А [5]:

Н — 2 — d,

Н - 1/А.

Показатель H рассчитывают по условиям:

1) если 0≤ H <1/2, то на рынке есть «тяжелый хвост» (отрицательная корреляция);

• 2)    если Н =1/2, то цены случайны, распределены случайно;

• 3)    если 1/2< H ≤1, то есть «тяжелый хвост» (корреляция положительна).

За точку R отсчета, согласно Херсту, можно взять ( T – время):

R -^Г.

Коэффициент Н находится из соотношений:

^R - aN^H, i г Ra (^ ln (aN)"

Здесь S – среднеквадратичное отклоне- задаваемая константа масштабирования, ние, R – размах для N наблюдений, a>0 – например, а =½.

Есть и экспериментальная формула Наймана:

H(t) = (-0.0011 ln(N) + 1.0136)

'n(^N)

Фрактальный подход к анализу структурных связей на строительном рынке эффективен и для цифровой экономики. Структуры – отражение способности к

эволюции, организационная структура на рынке – к нейтрализации структурных воздействий среды за счет эволюционного потенциала.