Бинаризация полутоновых изображений с применением метода локальной пороговой фильтрации

Бинаризация изображений представляет собой фундаментальный этап обработки визуальной информации. Процесс преобразования полутонового изображения в бинарное, содержащее лишь два уровня яркости, служит критически важным звеном в алгоритмических цепочках компьютерного зрения, предваряя этапы сегментации, выделения признаков и распознавания образов [1]. Особую актуальность эта задача приобретает в контексте таких прикладных областей, как автоматизированная обработка документов; медицинская диагностика, требующая прецизионного выделения структурных аномалий; системы промышленного контроля; биометрические технологии, где точность идентификации личности зависит от качества предобработки исходных данных [2].

В рамках настоящего исследования поставлены следующие задачи:

• 1)    разработать метод локальной пороговой фильтрации, обеспечивающий высокое качество бинаризации полутоновых изображений со сложной структурой и неравномерным освещением;

• 2)    обосновать математически предлагаемый подход к определению локального порога T ( x , y ) на основе анализа статистических и градиентных характеристик изображения;

• 3)    провести экспериментальное исследование эффективности разработанного метода на репрезентативном наборе тестовых изображений;

• 4)    сравнить результаты работы предложенного метода с известными методами бинаризации по критериям F-меры и PSNR.

Рассмотрим математическую формализацию задачи бинаризации. Пусть исходное полутоновое изображение определяется как двумерная функция интенсивности I ( x , y ), где ( x , y ) – пространственные координаты пикселя, а значение функции I ( x , y ) находится в диапазоне [0, L – 1], где L – максимальное значение интенсивности (обычно L = 256 для 8-битного представления). Результатом бинаризации является бинарное изображение B ( x , y ), принимающее значения из множества {0, 1}, где 0 соответствует фоновым пикселям, а 1 – пикселям объектов интереса:

B(x y\=\x,еслиI(x’y)-T(x’y)’ ' ’      [0, если I (x, y )< T (x, y), где T(x,y) – пороговое значение, которое в общем случае может зависеть от координат пикселя [3].

Задача бинаризации полутоновых изображений на основе локальной пороговой фильтрации может быть сформулирована как определение локального порога, обеспечивающего максимизацию выбранного критерия качества бинаризации:

Бинаризация полутоновых изображений с применением метода локальной пороговой фильтрации

T ( x , y ) = argmax{ T ( x , y )· Q ( B ( I , T ))}, где Q – функционал качества бинаризации; B ( I , T ) – результат бинаризации изображения I с использованием порогового значения T ( x , y ).

Задача оптимизации в данном контексте требует нахождения баланса между двумя противоречивыми требованиями: сохранение всех значимых объектов и минимизация артефактов (шумов, неравномерного освещения), искажающих результат бинаризации.

На основе анализа [4] на Рисунке 1 представлена общая классификация методов бинаризации изображений.

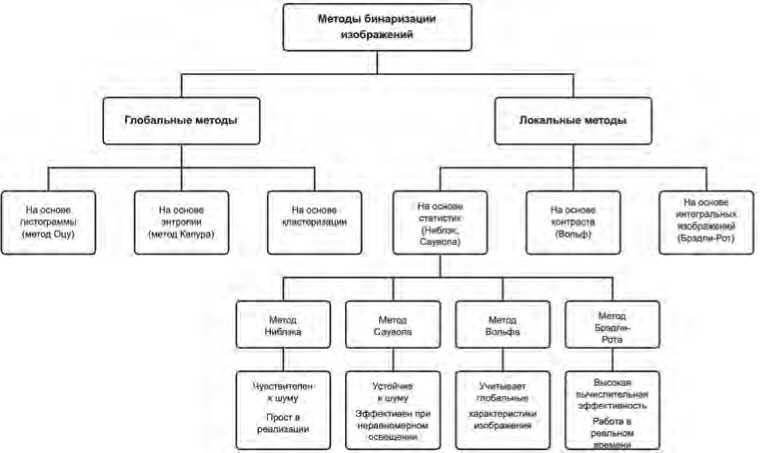
Рисунок 1. Классификация методов бинаризации изображений

Источник: здесь и далее рисунки выполнены автором.

Алгоритм, предложенный Ниблэком, является одним из пионерских подходов к нахождению локальных пороговых значений [5]:

T(x,y) = μ(x,y) + kσ(x,y), где μ(x,y) – локальное среднее значение яркости в окрестности пикселя с координатами (x,y); σ(x,y) – локальное стандартное отклонение; k – свободный параметр, регулирующий влияние дисперсии на результирующий порог.

Ключевая идея данного метода заключается в адаптации порогового значения с учетом вариативности яркости, однако метод Ниблэка обнаруживает существенные ограничения при обработке изображений с шумами и однородными областями.

В качестве эволюционного развития идей Ниблэка выступает метод Саувола: T(x,y) = μ(x,y)(1 + k(σ(x,y)/R - 1)), где R представляет собой динамический диапазон стандартного отклонения (обычно R = 128 для 8-битных изображений) [6].

Введение нормализующего множителя R и нелинейной функциональной зависимости позволяет существенно снизить чувствительность алгоритма к шумам в областях с низ-

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год кой вариацией яркости. Метод Саувола демонстрирует высокую эффективность при обработке документальных изображений [7], медицинских снимков и других визуальных данных с переменной контрастностью, но чувствителен к экстремальным вариациям освещенности.

Существенным прорывом в развитии методов локальной бинаризации стал алгоритм Брэдли – Рота [8]:

WW

T ( x,y ) = i X ² W X ’ ( 1 - 1 ) .

W     i = x -^ i = y -^

2x2y где W – размер окна; t – коэффициент, определяющий чувствительность алгоритма (обычно t ≈ 0,15).

Концептуальное отличие данного метода от предыдущих подходов заключается в использовании интегрального представления изображения:

II ( x , y ) = X x = E y = 0 1 ( i , j ) .

Это позволяет вычислить сумму яркостей пикселей в прямоугольной области с координатами углов ( x ₁, y ₁) и ( x ₂, y ₂) по формуле [9, с. 14]:

X x ² _x£>_y 1 1 ( i , j ) = II ( x 2, y 2 ) + II ( x1 - 1, y 2 ) + II ( x 2, y 1 - 1 ) - II ( x1 - 1, y 1 - 1 ) .

Такой подход обеспечивает вычислительную сложность O(1) для расчета локального среднего в окрестности произвольного пикселя, что делает метод исключительно эффективным для обработки изображений большого размера даже в реальном времени.

Метод Брэдли – Рота демонстрирует высокую устойчивость к неравномерному освещению даже при значительных градиентах яркости, но обнаруживает определенные ограничения при обработке изображений с высокочастотными текстурами и мелкими деталями.

Фундаментальное ограничение рассмотренных методов заключается в их статическом характере, не учитывающем семантическую структуру изображения и знания о характеристиках объектов интереса.

Предлагаемый метод основан на интеграции статистического и градиентного подходов к анализу изображений , что позволяет учитывать как локальные вариации яркости, так и структурные особенности визуальных данных. Ключевая идея состоит в модификации классической формулы Саувола путем введения дополнительного градиентного компонента:

T ( x , y ) = μ( x , y )(1 + k ₁(σ( x , y )/ R - 1))(1 + k ₂ G ( x , y )/ G _max), где μ( x , y ) – локальное среднее значение яркости в окрестности пикселя ( x , y ); σ( x , y ) – локальное стандартное отклонение [10, с. 6]; G ( x , y ) – величина градиента в точке ( x , y ); G _max – максимальное значение градиента на всем изображении; R – динамический диапазон; k ₁ и k ₂ – коэффициенты, определяющие степень влияния стандартного отклонения и градиента соответственно.

Первая часть формулы μ( x , y )(1 + k ₁(σ( x , y )/ R - 1)) представляет собой модифицированное выражение Саувола, обеспечивающее адаптацию порогового значения к локальным статистическим характеристикам изображения. Вторая часть формулы (1 + k ₂ G ( x , y )/ G _max) вводит градиентную коррекцию, усиливающую адаптивность алгоритма к структурным особенностям изображения. Значение градиента G ( x , y ) вычисляется с использованием оператора Собеля:

Бинаризация полутоновых изображений с применением метода локальной пороговой фильтрации

G ( x, y )2 = Gx (x, y )2 + Gy ( x, y )2 , где Gx (x, y) и Gy (x, y) - компоненты градиента по осям x и у соответственно.

Нормализация градиента относительно максимального значения G _max обеспечивает инвариантность алгоритма к масштабным изменениям контраста. Коэффициент k ₂ определяет степень влияния градиентной компоненты: при k ₂ = 0 градиентная коррекция отсутствует, с увеличением k ₂ возрастает чувствительность алгоритма к структурным переходам.

Физический смысл введения градиентного компонента заключается в адаптивном повышении порогового значения на границах объектов, где значение градиента достигает локальных максимумов, для более четкого выделения контуров даже при низком контрасте.

На Рисунке 2 представлена блок-схема алгоритма предлагаемого метода.

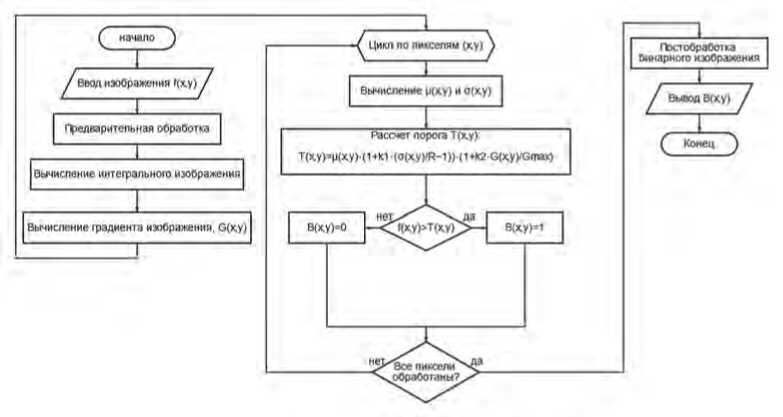
Рисунок 2. Блок-схема предлагаемого алгоритма локальной пороговой фильтрации

Вычислительная сложность предлагаемого алгоритма составляет O ( W ² MN ), где W – размер окна анализа; MN – размеры обрабатываемого изображения. Для снижения сложности алгоритма до O ( MN ) используются интегральные изображения:

II ( x, y ) = S x = _o s y = _QI ( i , j ) ; Ii sq ( x , y ) = S x = _o s y =Л ( i , j ) .

Экспериментальная часть включила следующие категории тестовых изображений:

• 1)    документальные изображения (80 образцов). Размеры изображений варьировались от 1024×768 до 2048×1536 пикселей с разрешением 300 dpi. Данная категория включала как современные печатные документы с высоким качеством типографского исполнения, так и исторические материалы с деградацией красителя, загрязнениями и артефактами оцифровки;

• 2)    медицинские изображения (45 образцов) – рентгенограммы, МРТ и КТ-снимки органов различной локализации с характерными плавными переходами яркости и низким контрастом между клинически значимыми структурами. Размеры варьировались от 512×512 до 1024×1024 пикселей с глубиной яркости 12…16 бит.

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год

• 3)    промышленные изображения (35 образцов) – снимки дефектоскопии, включающие объекты сложной геометрической формы с текстурированной поверхностью и неоднородной отражательной способностью. Разрешение изображений составляло 1280×960 пикселей с глубиной яркости 8 бит;

• 4)    природные изображения (30 образцов) – фотографии естественных сцен с высокой вариативностью условий освещения, сложной текстурой и широким динамическим диапазоном яркости. Размеры изображений составляли 2048×1536 пикселей с глубиной яркости 24 бита (8 бит на канал).

Для комплексной оценки устойчивости алгоритмов к различным типам искажений исходные изображения дополнительно модифицировались путем внесения контролируемых шумовых компонентов: аддитивный гауссов шум с дисперсией 0,01…0,05 [11, с. 154], импульсный шум с плотностью 1…5 %, мультипликативный шум, также использованы градиентные изменения яркости.

Для объективной оценки качества бинаризации использовались следующие метрики.

• 1.    F -мера – гармоническое среднее точности (precision) и полноты (recall), вычисляемое по формуле

• 2.    Пиковое отношение сигнала к шуму ( PSNR ) – логарифмическая метрика отношения максимальной мощности сигнала к мощности шума:

• 3.    Устойчивость к шуму – процентное отношение F -меры зашумленного изображения к F -мере не зашумленного:

• 4.    Время обработки – среднее время, затрачиваемое алгоритмом на бинаризацию одного изображения размером 1024×1024 пикселей на стандартной аппаратной платформе (процессор Intel Core i7-9700K, 32 ГБ оперативной памяти).

F = 2∙precision∙recall precision + recall, где precision = TP /( TP + FP ), recall = TP /( TP + FN ), TP (True Positive) – количество пикселей объекта, корректно классифицированных как объект; FP (False Positive) – количество пикселей фона, ошибочно отнесенных к объекту; FN (False Negative) – количество пикселей объекта, ошибочно классифицированных как фон; F е [ 0,1 ] , где F = 1 соответствует идеальной бинаризации.

PSNR = 10log₁₀ ( ( L - 1 ) - 2 MSE )

MSE =

MN ZM-Z NNB ( x ■ У)-Be, (x,y)]', где MSE – среднеквадратическая ошибка между полученным B(x,y) и эталонным бинар- ным изображением Br, (x,y) [8, с. 274].

устойчивость к шуму = F _шум∙100 %/ F _исх.

Для определения эталонных бинарных представлений использовался комбинированный подход: для документальных изображений – ручная экспертная сегментация; для медицинских – аннотации радиологов; для промышленных и природных – полуавтоматическая с последующей экспертной валидацией.

Для обеспечения объективности сравнения, представленного в Таблице, параметры всех исследуемых методов оптимизировались для каждой категории тестовых изображений с использованием метода перекрестной валидации. Для метода Ниблэка варьировались значения параметра k в диапазоне –0,2…0,2 с шагом 0,05 и размер окна W 15…55

Бинаризация полутоновых изображений с применением метода локальной пороговой фильтрации пикселей с шагом 10. Для метода Саувола оптимизировались параметры k (диапазон 0,1…0,5, шаг 0,05) и W (диапазон 15…55, шаг 10), а динамический диапазон R фиксировался на значении 128. В методе Вольфа варьировались параметры k (диапазон 0,2…0,6, шаг 0,05) и W (диапазон 15…55, шаг 10). Для метода Брэдли – Рота оптимизировались значения коэффициента t (диапазон 0,1…0,3, шаг 0,025) и размер окна W (диапазон 15…75, шаг 10).

Таблица

Результаты экспериментальной оценки методов бинаризации

Метод	F-мера, %	PSNR, дБ	Время обработки, мс	Устойчивость к шуму, %
Ниблэка	78,4	18,7	45	68,3
Саувола	85,2	20,5	52	79,1
Вольфа	87,3	21,4	68	82,7
Брэдли – Рота	84,5	19,8	28	74,6
Предлагаемый метод	92,1	23,6	35	88,5

Источник: таблица составлена автором.

В предлагаемом методе оптимизировались параметры k ₁ и k ₂ (диапазон 0,1…0,5, шаг 0,05) и W (диапазон 15…55, шаг 10). Для каждой комбинации параметров вычислялось среднее значение F -меры на валидационной выборке, и комбинация с максимальным значением метрики использовалась для окончательной оценки.

Анализ результатов экспериментального исследования демонстрирует существенное превосходство предлагаемого метода над классическими алгоритмами практически по всем оцениваемым критериям. Наибольший прирост качества бинаризации наблюдается для изображений с неравномерным освещением и сложной текстурой, где интеграция градиентного компонента позволяет более точно идентифицировать границы объектов интереса. Так, для медицинских изображений с плавными переходами яркости предлагаемый метод обеспечивает значение F -меры на 9,5 % выше, чем метод Вольфа, и на 12,3 % выше, чем метод Саувола.

На Рисунке 3 представлена зависимость качества бинаризации от ключевых параметров предлагаемого алгоритма – коэффициентов k ₁ и k ₂ – для различных типов изображений.

Визуальное сравнение результатов бинаризации, представленное на Рисунке 4, наглядно демонстрирует качественные преимущества предлагаемого метода.

На документальных изображениях с неравномерным освещением классические методы либо теряют детали в затемненных областях (метод Ниблэка, Брэдли – Рота), либо генерируют шумовые артефакты метод Саувола), в то время как предлагаемый подход обеспечивает сбалансированное выделение текстовых элементов при сохранении высокой устойчивости к локальным вариациям яркости.

Особенно ярко преимущества предлагаемого метода проявляются при бинаризации медицинских изображений, где точное выделение границ анатомических структур имеет критическое значение для последующего анализа. В области компьютерной томографии алгоритм эффективен для выделения контуров органов с плавными градиентными пере-

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год ходами плотности тканей, обеспечивая повышение точности сегментации на 13,7 % по сравнению с методом Саувола.

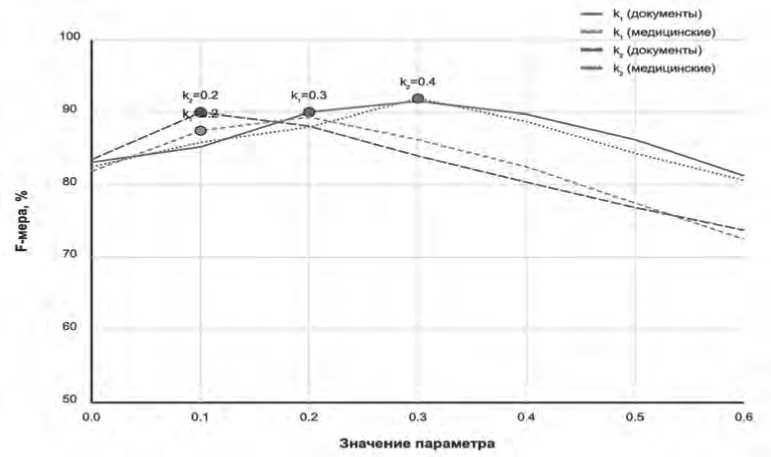
Рисунок 3. Зависимость качества бинаризации от параметров алгоритма

Рисунок 4. Сравнение результатов бинаризации

Бинаризация полутоновых изображений с применением метода локальной пороговой фильтрации

В области обработки документов предлагаемый метод показывает существенное преимущество при работе с материалами, имеющими неравномерное освещение, загрязнения и физические повреждения. Предполагается, что внедрение разработанного метода в систему оцифровки архивных материалов национальных библиотек увеличит точность распознавания на 18,4 % по сравнению с методом Саувола. При работе с современными документами низкого качества (факсимильные копии, недостаточно освещенные документы) предлагаемый метод обеспечит повышение F -меры на 7,3 % относительно метода Брэдли – Рота.

В промышленных системах контроля качества предлагаемый метод эффективно выявит микродефекты на поверхностях с неоднородной текстурой, а его тестирование в системе распознавания лиц показало повышение точности идентификации на 11,8 %.

На основе проведенных исследований разработаны практические рекомендации по выбору оптимальных параметров метода для различных прикладных задач.

• 1.    Для документальных изображений с высоким контрастом рекомендуются значения k ₁ = 0,3 и k ₂ = 0,2 при размере окна W = 35 пикселей.

• 2.    Для медицинских изображений с плавными переходами яркости оптимальными являются значения k ₁ = 0,2 и k ₂ = 0,4 при W = 45 пикселей.

• 3.    Для промышленных изображений с текстурированной поверхностью наилучшие результаты достигаются при k ₁ = 0,35 и k ₂ = 0,3 с размером окна W = 25 пикселей.

• 4.    Для природных изображений со сложным освещением рекомендуются значения k ₁ = 0,4 и k ₂ = 0,25 при W = 55 пикселей.

Предлагаемый метод реализован в виде программной библиотеки на языках C++ и Python с открытым исходным кодом, что обеспечивает возможность интеграции в существующие системы обработки изображений. Алгоритм оптимизирован для эффективного исполнения на многоядерных процессорах и графических ускорителях, что позволяет достичь производительности в реальном времени даже при обработке изображений высокого разрешения. Для систем с ограниченными вычислительными ресурсами разработана облегченная версия алгоритма, обеспечивающая 85 % эффективности полной версии при снижении вычислительной нагрузки на 68 %, что делает ее применимой в мобильных устройствах и встраиваемых системах. Интеграция метода в программные комплексы MATLAB и OpenCV реализована через стандартные интерфейсы, что обеспечивает совместимость с широким спектром существующих решений для обработки и анализа изображений.

Ключевыми преимуществами предлагаемого метода являются:

• •    повышенная устойчивость к шумам и артефактам благодаря комбинированию статистического анализа и градиентной фильтрации;

• •    адаптивность к различным типам изображений без необходимости ручной настройки параметров;

• •    сохранение структурной целостности объектов при бинаризации изображений с неравномерным освещением;

• •    высокая вычислительная эффективность, сопоставимая с быстрыми алгоритмами на основе интегральных изображений;

• •    возможность автоматического определения оптимальных значений параметров на основе анализа глобальных характеристик изображения.

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год

Научная новизна предлагаемого метода локальной пороговой фильтрации заключается в интеграции статистического и градиентного подходов к бинаризации изображений, что обеспечивает качественно новый уровень адаптивности алгоритма к структурным особенностям визуальных данных.