Бинарная линза: исследование локальных фокусов

Амплитудная зонная пластинка Френеля, которая использовалась лордом Рэлеем ещё в 1871 году, действует как линза с множеством фокусов, каждый из которых содержит некоторую долю падающей на пластинку энергии. При этом в основном фокусе содержится всего около 10% всей энергии. Столь низкая эффективность бинарной линзы по сравнению с рефракционной препятствовала её использованию во многих приложениях.

Множество усилий было сосредоточено на увеличении эффективности «плоской» линзы. В частности, в 1898 году Вуд предложил фазовый вариант бинарной зонной пластинки [2], который позволял повысить эффективность в основном фокусе до 40%.

Френелевская линза, исполненная в виде кусочно-гладкого рельефа, теоретически позволяет достичь 100%, а приблизиться к этой эффективности можно за счёт многоуровневого рельефа [3]. Однако при этом погрешности изготовления влияют как на качество изображения, так и на эффективность [4].

В данной работе наличие у бинарной дифракционной линзы множества локальных фокусов рассматривается с позитивной точки зрения потенциального использования для повышения разрешения.

Как правило, локальные фокусы бинарной линзы исключаются из рассмотрения, потому что доля энергии, которая на них приходится, уменьшается обратно пропорционально квадрату номера локального фокуса [5, 6]. Однако при этом упускается из виду тот факт, что поперечный размер локального фокуса также уменьшается пропорционально номеру, а, следовательно, при меньшей площади фокального пятна его интенсивность оказывается соизмеримой с интенсивностью основного максимума [7]. Этот факт может быть использован для улучшения разрешения фокусирующих систем.

В данной работе в рамках скалярной теории (как параксиальной, так и непараксиальной) исследуются такие характеристики локальных фокусов, как размер фокального пятна и его интенсивность.

Результаты численного моделирования и эксперимент подтверждают аналитический анализ.

1. Параксиальный анализ осевого распределения для осесимметричных оптических элементов с кусочно-постоянной функцией пропускания

Распространение поля т ( r ), обладающего осевой симметрией, в параксиальном приближении можно описывать с помощью преобразования Френеля:

х к х I ik Р L F ( р , z ) = — exp( ikz )exp —^!— x iz                I 2 z )

, с I ikr2 | I krр I x t(r) exp ---- Jo —— r dr,

0 к 2 z 7 к z 7

где к = 2 п / % - волновое число, % - длина волны излучения, R – радиус входной апертуры.

Если т(r) принимает кусочно-постоянные зна чения:

/7 F < F < F

7 X       a n , r n ~ r <  r n + 1,

t( r) = <

[ 0, r > r„ = R, то выражение (1) на оптической оси:

к             n    r n + ¹      I ikr ² 1

FT (0, z) = — exp(ikz)Z an J exp I      l r dr iz           n=0    ,      12 z J rn можно вычислить аналитически.

Учитывая, что b

J exp(iвr2)rdr = a ,

= 2iP texp (i в b 2)- exP (i в a 2)]

выражение (3) можно переписать:

k         2 z ^N

F T ^{(0, z} ) = - ^e xp ⁽ i^kz ) — L a n iz           2 ik n =0

^Г ikr 2i expl ——

V 2 z

^Г ikr² exp l —

V 2 z

I ^{Г 2}

= exp( ikz ) a ₀ exp ——

I 0 I 2 z

(ikr 2 1 N - ■ ikr

^- a N exp I      |⁺ L ( a n

V ² z j n =1

^{Г ikr} n И a n -1 ) ^expl _n If .

V 2 z JI

2. Анализ осевого распределения для бинарной линзы

Бинарный аналог непрерывной фазовой функции пропускания y ( r ) оптического элемента можно представить в следующем виде для фазового элемента:

^T ph ⁽ r ) = exp i I { 1 ^- sgn ( sin | u ( r ^{) ]}) } =

Из (5) следует, что если все a_n равны некоторой константе a (соответствует кольцевому отверстию с радиусами r ₀ и r_N ), то сумма обнуляется:

F (0, z ) =

1, sin [ v ( r ) ] > 0, - 1, sin [ v ( r ) ] < 0,

I     Г ikr, 2

= a exp( ikz ) < exp ---- I I 2 z

^Г ikr 2 exp I V

V 2 z

= 2 ia exp( ikz ) exp

Г ik (rN - r0) 1

в

x sin

V

Г k (r02 + rN) 1

4 z

J

x

.

4 z

V           J

Т.о. в параксиальном случае любое кольцевое отверстие с постоянной пропускающей функцией приводит к формированию осциллирующего с постоянной амплитудой осевого распределения с нулевыми значениями в точках z m = ( r ₀ ² + r N ) /2 m X и максимумами при z mm = ( r ₀ ² + r N ) /(2 m + 1) X , где m - целое. «Последний» максимум будет располагаться на расстоянии z 0 = ( r ₀ ² + r N ) /X от входной плоскости.

Если функция пропускания входного поля (2) имеет только два значения внутри области радиуса R , например, бинарный фазовый или амплитудный оптический элемент освещается равномерным излучением, то выражение (5) примет следующий вид для бинарного фазового элемента:

I       Г ikrn21

F ph ^{(0, z} ) = ^exp⁽ i^kz ) 1^- exp |       |⁺

I         V 2 z j

²1     N ^-              2 ih-¹ 11

+ ( - 1) ^{N + 1} exp I ikr N | + 2 L ( - 1) n ^{+ 1} exp l '(   | f , (7)

V 2 z J _n= 1                 I 2 z J I

a ₀ = - 1

и для бинарного амплитудного элемента:

I    Г ikr21

^F amp ^(0, z ) = exp⁽ ikz ) S exp l -7— | ⁺

I V 2 z J

+ ^{1 - ( - 1)}

I ^N + ¹       41a-       N - 1             (ikr¹ 11

ikrN   , X^ / i\« ikr I /o\

---exp / I⁺ L ^{( - 1)} exp l |f , ⁽⁸⁾

V 2z J n=1            V 2z JI

a ₀ = 1.

Как видно из сравнения выражений (7) и (8), вклад суммы при использовании фазового элемента удваивается.

и для амплитудного элемента:

^T amp ⁽ r ) = 2 { 1 ⁺ sgn ( sin [ V ⁽ r ) ] ) } =

= I 1, sin [ v ( r ) ] >  0,

[ 0, sin [ y ( r ) ] < 0.

Координаты фазовых скачков между значениями 0 и п фазового элемента, а также между пропускающими и поглощающими зонами амплитудного

элемента, вычисляются из выражения:

sin [ y ( r ) ] = 0 ^ y ( r ) = п n .

Для фазовой функции параболической фокусным расстоянием f :

k

v( r) = - 2fr радиусы зон имеют следующий вид:

линзы с

r n ²

В

= 2lnf. = n Xf.

2.1. Параксиальный случай соответствии с формулами, полученными в

первом разделе, бинарная фазовая линза будет формировать следующее осевое распределение ⁽ r 0 = ⁰, r N = R ^):

I                   Г ikR21

F phL ^(0, z ) = exp⁽ ikz ) S^{- 1 + ( - 1)}   exp l "Г— | ⁺

2 z

, ^{[                    V J} (14)

+ 2 ^ -1 ( - 1) ^{n + 1} exp Г i ^ nf- n =1                  V z .

с экстремальными значениями в точках локальных фокусов z m = f / m :

^F phL ( ⁰, z m ) = exp^{( ikz} m ) { ^{- 1 +}

Г _ikR ² 1     N -¹                     1 (15)

+ ( - 1) ^{N + 1} exp ---- + 2^ ( - 1) n ^{+ 1} exp ( i п nm ) k

V 2 z m J    tf                   I

Независимо от чётности числа зон N в выражении (15) сумма будет минимальной при чётных m и максимальной при нечётных m :

2]Г( - 1) n ^{+ 1} exp ( i п nm ) =

n =1

[ 1 - ( - 1) N ^{+ 1} , m - чётные , s

[ 2( N - 1), m - нечётные .

Аналогичный результат получается для амплитудной бинарной линзы:

F ampL ^(0, z m ) =

1 - ( - 1) N ^{+ 1}      I ikR ² )

= exp( ikz m ) Д +--------- exp l-—I +        (17)

I ²          I ² z m J

N -1                              3

+ E ( - 1) n exp exp ( i n nm ) ^ , n =1

где

N -1

E (-1)n exp (innm) = n=1

j- ( 1 - ( - 1) ^{N + 1} ) /2, m - чётные , | ( N - 1), m - нечётные .

В этом случае значения интенсивности в локальных фокусах будут в 4 раза меньше, чем для фазового элемента.

Однако в параксиальном случае все локальные фокусы имеют одинаковое значение, что не будет соответствовать реальности при приближении к плоскости оптического элемента. Рассмотрим непараксиальный подход.

2.2. Непараксиальный случай

В непараксиальном случае можно воспользоваться интегральным преобразованием Рэлея-Зом-мерфельда первого типа:

ikℓ z                      е I

E(и,v,z) = -—ДЕ0(x,y)-гlik-- Idxdy,

2 П v            I V

"U где E0(x,y) - входное поле, L0 - область, в которой задано входное поле, I = Д(u - x)2 + (v - y)2 + z2 .

Для осевого распределения при дифракции плоской волны на круглом отверстии радиусом R известно аналитическое выражение [8-10]:

F r (0, z ) = exp ( ikz ) -

. z 7 exp ( ik^R ² + z²

Rr+TF  ⁽

Также можно получить аналитический вид для случая дифракции на кольце с радиусами а и b :

F ab (0, z ) =

= z

exp ( ik V a ² + z ² ) exp ( ik^b ² + z ² )

.

V b ² + z ²

+ z ²

Для кусочно-постоянного элемента (2):

N -1

FT (0, z) = E an X n=0

X

exp ( ikz J 1 + Rf z ² ) exp ( ikzR 1 + r „ ²₊₁/ z ² ) 7^{1 +} r n 7 ^{z 2}            V¹¹ r^ z

Для фазовой бинарной линзы a n = ( - 1) n ^{+ 1} , '" = n X f при z m = f / m получим:

r_n² _ X nm ²

= zm      f и осевое распределение:

F (0, zm ) = exp l   J1+ X nm2/f

V m

R 1 + X nm ²/ f

N -1

= e ( - 1) ^{n + 1}

n =0

exp [ — R 1 + X ( n + 1) m ² / f V m                J

71 + X ( n + 1) m ²/ f

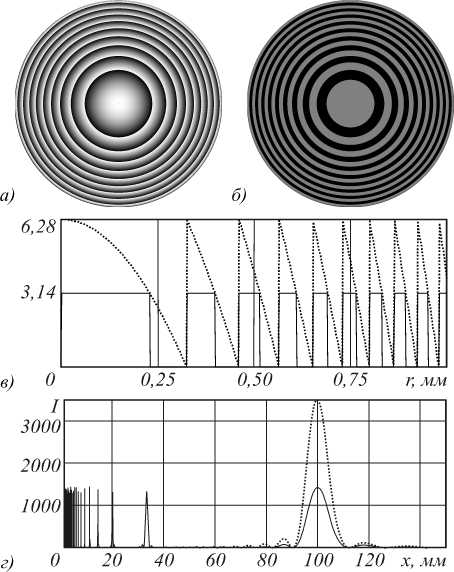
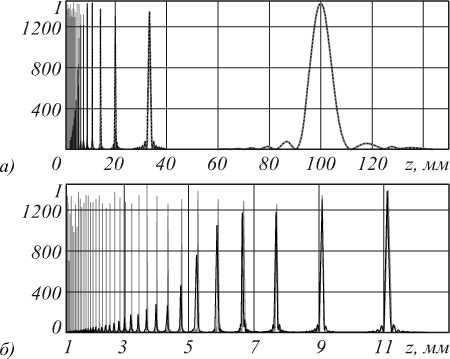
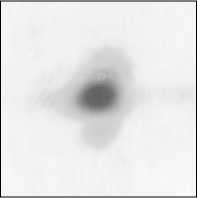
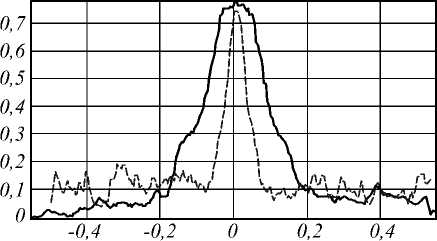
Рассмотрим случай, когда

(kf/m)(XNm2/f)

Для длиннофокусной линзы с невысокой числовой апертурой (например, NA = 0,01) отношение f / R ~ 100 и число включённых в рассмотрение локальных фокусов будет значительно, особенно для микроэлементов.

Для данного случая можно применить приближение 71 + XNm²/f = 1 + XNm²/2 f (погрешность которого для n< N будет ещё меньше), и тогда выражение в (24) примет следующий вид:

^FphL (⁰, zm > zp ) =

= exp (ikz_m) E(-1) n⁺¹exp (innm )x              (25)

n=0

_X"      ^1exp^(inm)    "

1+ Xnm²/2f 1 + X(n +1)m²/2f '

Для чётных m фазовые множители внутри суммы примут единичное значение, а выражение в квадратных скобках можно заменить на приближённое:

_1 + Xnm²/2 f " 1 + X(n +1)m²/2 f _ ~

_ X m²          1

~ "fj ' 1 + X(2n +1)m²/2 f'

Для нечётных m можно провести аналогичные рассуждения. В результате получим:

^FphL ( ⁰zm > zp )= exP ( ikzm )^X

на оптической оси:

х 5

% m² N-¹ 2fr ^

(-1) n⁺¹

N-1

2Z

n=0

1 + %(2 n +1) m²/2 f

■, m - чётное,    p^x

N-1

FphL (0, Zm ) = 2 m %ff £ (-1) n х n =1

f г Г <

------77—, m - нечётное. 1 + % nm2/2 f

х 5

n

2 m² n % + f

V

f²

Заметим, что при чётных m на оптической оси теперь ненулевое (хотя и малое) значение, которое увеличивается с ростом m. Значения в нечётных локальных фокусах медленно убывают с ростом m.

Для выражения (26) можно дать оценки сверху и снизу:

\ n +1

—5----:---х

2 m²( n +1)% + f

Г (

х exP ik   (n +1)%f +

L V

f²

2 m 7/( n +1)%f

>.

L ( Zm )< FphL ( 0, Zm > Zp )< R ( Zm ) ,              (27)

где

L ( zm ) = exP ( ikzm ) ^

1 f %m²Y

— ------7 , m - четное,

2(f + %m2 J

2f

2N -,-----------7, m - нечётное.

(2f+ %Nm2)

f % m2

Приближённо модуль выражения (30) оценить как модуль первого слагаемого:

|FphL (0, Zm )| < ²m V%f -^2— ~ 7 ^f,

1          1          2 m % + f m \ %

можно

т.е. интенсивность будет уменьшаться пропорционально m².

, x , x I---------7, m - чётное,

R ( zm ) = exP (ikzm ) 5 2 f + %m

12N, m - нечётное.

Отношение локальных фокусов к глобальному по нижней границе:

= 2f + %N = 1 + R2/2f2

^Пm = 2f + %Nm² ~ 1 + R²m²/2f² '

_                                         1 + 5-10^-5

В частности, при f / R = 100 n =-----т---7 ^m 1 + 5 m²10^-5

∼

при m<10. Конкретнее, при m = 9 n9 ~0,99.

Таким образом, для линзы с низкой числовой апертурой значительное число локальных фокусов

имеют практически такую же интенсивность, как и основной фокус. Однако в области, близкой к опти-

ческому элементу, нельзя использовать параксиальное приближение. В этом случае выражение (22) удобнее записать в следующем виде:

N-1

FT (0, Z) = Z£ an х n=1

. 2 ^

exP ikr_nx 1 + z4

V

r n

\ r

n J

1 + z2

r

n

'        z^

exP ikrn+J^{1 +} —

V v     rn+1

2 z rn+U 1+ 2

\      rn+1

Л "

J

.

Учитывая близость к оптическому элементу

rn V^{1 +}z 7 rn²” rn⁺z 7²rn , тогда для бинарной линзы в

локальных экстремумах

r + Z2 /2 r nmn

f (2 m2 n % + f)

2 m²xj n %f

3. Численное моделирование для фазовой бинарной линзы

Численное моделирование для линзы радиусом R = 1 мм и фокусным расстоянием f = 100 мм проводилось с помощью расчёта преобразования Френеля (1) и непараксиального распространения через угловой спектр, который полностью соответствует интегралу Рэлея-Зоммерфельда (19), но в условиях радиальной симметрии задачи позволяет сократить время вычислений [11]. Длина волны была принята λ = 532 нм.

На рис. 1 показаны результаты моделирования в рамках параксиального приближения для многоуровневой линзы, фаза которой представлена на рис. 1а, и бинарной линзы, фаза которой представлена на рис. 1б. Радиальные сечения фазовых распределений показаны на рис. 1в. Осевое распределение интенсивности, формируемое каждой из линз, приведено на рис. 1г.

Как видно из рис. 1, многоуровневая дифракционная линза не имеет дополнительных фокусов. Бинарная же линза имеет множество локальных фокусов, интенсивности которых равны. Интенсивность основного фокуса бинарной линзы составляет примерно 41% от интенсивности фокуса многоуровневой линзы. Локальные фокусы располагаются в плоскостях Zm = f / m , m - нечётное.

При использовании непараксиальной модели значение интенсивности в локальных фокусах перестаёт сохраняться при приближении к плоскости оптического элемента. Интенсивность локальных фокусов примерно одинаковая вплоть до m = 7 (рис. 2а). Начиная с локального фокуса, соответствующего m = 13, наблюдается заметное падение интенсивности (рис. 2б).

Таким образом, результаты моделирования подтверждают аналитические выкладки второго раздела.

Рис. 1. Результаты параксиального моделирования: фаза многоуровневой линзы (а), фаза бинарной линзы (б), радиальные сечения фазовых распределений (в), осевое распределение интенсивности, формируемое каждой из линз (г) (в, г: точечная линия – для многоуровневой линзы, сплошная линия – для бинарной линзы)

Рис. 2. Сравнение осевого распределения интенсивности, формируемого бинарной линзой в рамках параксиальной (серая линия) и непараксиальной (чёрная линия) моделей: вблизи основного фокуса (а) и вблизи оптического элемента (б)

Характеристики локальных фокусов в рамках непараксиальной модели по отношению к основному фокусу, включая интенсивность, продольную ширину по полуспаду интенсивности (FWHM_l) и поперечную ширину по полуспаду интенсивности (FWHM_t), приведены в табл. 1.

Как видно из рис. 2б, в непараксиальной модели положения локальных фокусов несколько смещаются к плоскости оптического элемента. В табл. 1 приведены результаты с учётом этого смещения.

Таблица 1. Сравнительные характеристики локальных фокусов в рамках непараксиальной модели по отношению к основному фокусу (FWHM_l= 9,357 мм, FWHM_t = 0,028 мм)

m	Положение, мм	Относительная интенсивность	Относительная FWHM_l	Относительная FWHM_t
1	100,00	1,000	1,0000	1,0000
3	33,33	0,999	0,1144	0,3321
5	20,00	0,998	0,0423	0,2001
7	14,27	0,996	0,0209	0,1419
9	11,09	0,991	0,0124	0,1089
11	9,06	0,958	0,0084	0,0898
13	7,66	0,861	0,0063	0,0764
15	6,63	0,824	0,0047	0,0659
17	5,84	0,766	0,0037	0,0572
19	5,22	0,557	0,0036	0,0511
21	4,71	0,328	0,0045	0,0485
23	4,27	0,254	0,0046	0,0365
25	3,92	0,216	0,0046	0,0339

Из табл. 1 можно заметить, что уменьшение продольной ширины фокусов происходит значительно быстрее, чем поперечной. Однако с некоторого момента продольный размер перестаёт уменьшаться.

Вплоть до локального фокуса с номером m =21 поперечный размер светового пятна уменьшается пропорционально номеру фокуса, однако это компенсирует падение интенсивности лишь до фокуса с номером m =7. Это значит, что далее мы выходим из области параксиальности, которая определятся границей zp = R (2R/λ)1/3 ≈ 15 мм, и попадаем в промежуточную зону - зону между зоной параксиальности и зоной, в которой начинается падение интенсивности пропорционально квадрату номера. Такой закон падения интенсивности наблюдается, если расстояние до оптического элемента менее радиуса элемен- та. В этом случае радиусы локальных фокусов перестанут уменьшаться (рис. 3в).

Таким образом, можно выделить три зоны вдоль

оптической оси, соответствующие различным соотношениям интенсивности в локальных фокусах:

1) зона одинаковой интенсивности,

z > zp = R

2 R Y/3

%

б)

Рис. 4. Экспериментально зафиксированные распределения интенсивности (негатив) в основном и ближайшем локальном фокусах бинарной фазовой линзы: z1=2010 мм (а), z3=670 мм (б)

2) промежуточная зона приближённо линейного падения интенсивности, R < z < z_p ,

3) зона падения интенсивности пропорционально квадрату номера фокуса, z < R .

Рис. 3. Различные зоны на оптической оси: зона сохранения интенсивности в локальных фокусах (а), зона линейного падения (б), зона квадратичного падения (в)

4. Экспериментальные результаты

Экспериментальные результаты были получены с помощью фазовой бинарной маски, выведенной на динамическом транспаранте CLR OPTO. Маска размерностью 1024x1024 отсчёта рассчитана для радиуса R =7,5 мм и фокального расстояния f =2000 мм. Для освещения использовалось лазерное излучение с длиной волны % = 532 нм.

На рис. 4, 5 представлены результаты, зафиксированные в основном и ближайшем локальном фокусах бинарной фазовой линзы. Видно, что происходит уменьшение размера фокального пятна при небольшом уменьшении интенсивности. Положения фокусов оказались несколько сдвинуты от плоскости элемента из-за небольшой расходимости освещающего транспарант лазерного пучка.

Рис. 5. Сечения экспериментальных интенсивностей в основном и ближайшем локальном фокусах бинарной фазовой линзы: z1=2010 мм (сплошная линия), z3=670 мм (пунктирная линия)

В табл. 2 приведены сравнительные характеристики фокусов, полученные в эксперименте и при численном моделировании (экспериментальные результаты приведены перед разделителем с указанием погрешности измерений, численные – после разделителя).

Эффективность рассчитывалась как отношение энергии в фокальном пятне к общей энергии, падающей на бинарную линзу. Как видно, она падает пропорционально квадрату номера локального фокуса. Однако за счёт того, что радиус локальных фокусов также уменьшается пропорционально номеру фокуса, интенсивность остаётся близкой к значению в основном фокусе.

Наблюдается достаточное согласование численных и экспериментальных результатов: пропорциональное уменьшение размеров локального фокуса по сравнению с основным. Размер фокусов в эксперименте оказался несколько больше ожидаемого, что связано со сложностью юстировки при использовании динамического транспаранта и с низким разрешением камеры. В дальнейшем планируется выполнить эксперименты с дифракционным оптическим элементом на кварцевой подложке.

Таблица 2. Сравнительные характеристики локальных фокусов, полученные в эксперименте и при численном моделировании

m	Положение, мм	Относительная интенсивность	FWHM_t, мм	Эффективность, %
1	2010+10 / 2000	1,00 / 1,00	0,18+0,03 / 0,142	31,46 / 26,43
3	670+10 / 667	0,95 / 0,99	0,07+0,02 / 0,047	2,51 / 2,81

Таким образом, аналитические выкладки подтверждаются не только численными, но экспериментальными результатами.

Заключение

В работе в рамках скалярной теории дифракции (как параксиальной, так и непараксиальной) выполнен анализ осевого распределения, формируемого бинарной линзой (зонной пластинкой). При этом эффективность амплитудной зонной пластинки в 4 раза ниже фазовой.

Аналитически показано, что для линз с невысокой числовой апертурой несколько локальных фокусов, следующих сразу за основным, имеют интенсивность, близкую к интенсивности основного фокуса. Это связано с пропорциональным номеру уменьшением поперечных размеров локальных фокусов. Таким образом, падение энергии, приходящейся на каждый локальный фокус пропорционально квадрату номера, компенсируется соответствующим уменьшением площади локального фокуса.

Такое поведение характерно для зоны, соответствующей условиям параксиальности. Также выделены ещё две зоны – близкая к оптическому элементу, где поперечный размер фокального пятна перестаёт уменьшаться и, соответственно, интенсивность падает пропорционально квадрату номера фокуса, а также промежуточная зона, падение интенсивности в которой можно считать приблизительно линейным.

Результаты численного моделирования и эксперимент подтверждают аналитические исследования.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF PG08014-1), грантов РФФИ 10-07-00109-а, 10-07-00438-а, грантов Президента РФ поддержки ведущих научных школ НШ-7414.2010.9 и молодого доктора наук МД-8026.2010.2.