Бинарный генетический алгоритм с декомпозицией на основе оценки распределения для задач глобальной оптимизации высокой размерности
Автор: Сопов Е.А.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 4 т.17, 2016 года.
Бесплатный доступ
В последние годы существенно увеличилась размерность многих практических задач оптимизации. Подобные задачи глобальной оптимизации высокой размерности (large-scale global optimization, LSGO) имеют несколько сотен или тысяч переменных и являются несепарабельными. Более того, практические задачи оптимизации часто сложны для детального анализа и рассматриваются как модели типа «черный ящик», следовательно, при решении этих задач применимы только методы прямого («слепого») поиска. Наиболее эффективные подходы используют популяционные методы случайного поиска и основаны на идеях кооперативной коэволюции с декомпозицией задачи по переменным. Подобные алгоритмы в основном ориентированы на задачи с вещественными переменными и не могут быть применены к задачам с дискретными и смешанными переменными. Предложен новый подход, основанный на применении сочетания бинарного генетического алгоритма и алгоритма оценки распределения (Еstimation of distribution algorithm, EDA). Бинарный генетический алгоритм решает основную задачу оптимизации, алгоритм EDA используется для оценки статистики, накопленной по результатам прошлых этапов поиска генетическим алгоритмом, и дальнейшей декомпозиции задачи путем фиксации перспективных значений генов в хромосоме. Предложенная декомпозиция задачи на основе EDA-алгоритма обладает свойствами основных методов решения задач оптимизации высокой размерности: метода случайной группировки генов и метода анализа динамики генов. Обсуждаются обычная версия предложенного подхода и островная модель, позволяющая реализовать алгоритм на параллельных компьютерах. Представлены результаты численных экспериментов на множестве тестовых задач, используемых в соревнованиях по глобальной оптимизации высокой размерности в рамках конференций IEEE CEC. Результаты демонстрируют, что предложенный подход обладает эффективностью, сравнимой с другими известными эффективными подходами (победителями и участниками соревнований), и в то же время может применяться к задачам оптимизации с любыми переменными, так как используется бинарное представление решений.
Бинарный генетический алгоритм, алгоритм оценки распределения, декомпозиция задачи оптимизации, глобальная оптимизация высокой размерности
Короткий адрес: https://sciup.org/148177652
IDR: 148177652 | УДК: 519.85
Текст научной статьи Бинарный генетический алгоритм с декомпозицией на основе оценки распределения для задач глобальной оптимизации высокой размерности
Введение. Эволюционные алгоритмы (ЭА) доказали свою высокую эффективность при решении многих сложных прикладных задач оптимизации. Тем не менее, их эффективность обычно чувствительна к размерности задачи и падает с существенным ростом числа переменных. Сложные задачи глобальной оптимизации, в которых число переменных может достигать нескольких сотен или тысяч, часто относят к классу задач глобальной оптимизации высокой размерности (Large-Scale Global Optimization, LSGO). Несмотря на то, что такие задачи были известны всегда, в отдельный класс они были выделены сравнительно недавно и получили развитие лишь в последние годы. Сегодня LSGO-задачи возникают все чаще, так как растут вычислительные мощности компьютерной техники, пропускная способность каналов связи и, как следствие, объемы и размерность собираемых и обрабатываемых данных. В частности, в аэрокосмической отрасли модели с большим числом переменных используются для моделирования и анализа больших данных, например, по результатам огневых испытаний двигателей, спутниковой и аэрофотосъемки поверхности земли, при проектировании бортовых и наземных систем управления и т. д.
Известны классы задач оптимизации большой размерности, которые не представляют трудностей ни для традиционных методов математического программирования, ни для более продвинутых подходов (например, задачи линейного программирования). В то же время, многие практические задачи являются малоизученными и сложными для детального анализа. В этом случае их принято рассматривать как модели типа «черный ящик», в которых возможны только оценки целевой функции в конкретной точке, но информация о свойствах ландшафта целевой функции отсутствует. Часто к моделям типа «черный ящик» относят и задачи, в которых целевые функции заданы явно (аналитически), но сложность модели не позволяет выявить полезные для оптимизации свойства. Подобные задачи представляют сложность и для ЭА, так как не представляется возможным выбрать и настроить под задачу конкретный алгоритм. Более того, практические LSGO-задачи часто оказываются несепарабельными, из-за чего не удается снизить размерность задачи путем ее декомпозиции по переменным.
Несмотря на вышеперечисленные трудности, существуют различные эвристики для эффективного решения LSGO-задач. В настоящее время предложено достаточно много различных подходов для задач с вещественными переменными [1]. Однако многие прикладные задачи связаны с анализом различных сложных структур данных, которые выражены в разных шкалах и не могут быть представлены только вещественными переменными. В таких случаях все переменные задачи переводятся в одну из простейших шкал. На практике часто используется бинарное представление решений и бинарные генетические алгоритмы (ГА). Однако, как показывает обзор различных информационных источников, на сегодняшний день алгоритмы для бинарных LSGO-задач развиты недостаточно.
В данной работе предложен новый подход для решения задач глобальной оптимизации высокой размерности, который использует бинарный ГА с декомпозицией задачи на основе алгоритма оценки распределения (Еstimation of Distribution Algorithm, EDA). Бинарный генетический алгоритм решает основную задачу оптимизации, алгоритм EDA используется для оценки статистики, накопленной по результатам прошлых этапов поиска ГА, и дальнейшей декомпозиции задачи путем фиксации перспективных значений генов в хромосоме.
В настоящее время существует множество подходов к LSGO-оптимизации, которые можно объединить в две большие группы: не использующие декомпозицию методы и методы на основе кооперативной коэволюции. Первая группа методов в основном связана с модификацией стандартных эволюционных и генетических операторов. Наилучшие результаты, тем не менее, достигаются методами второй группы, которые осуществляют декомпозицию задачи на задачи меньшей размерности путем группировки переменных. Методы на основе кооперативной коэволюции включают три основных этапа: декомпозиция задачи, решение выделенных подзадач оптимизации и сборка полного решения из найденных компонент. Очевидно, что этап декомпозиции является наиболее важным. Наиболее популярными являются следующие подходы к группировке переменных при декомпозиции задачи: статическая группировка по некоторому правилу (static grouping) [2], динамическая случайная группировка (random dynamic grouping) [3] и адаптивная группировка (learning dynamic grouping) [4; 5]. Большой обзор методов для LSGO-оптимизации предложен в [1]. Как видно из данного обзора и других работ, большая часть исследований посвящена задачам с вещественными переменными.
Алгоритмы оценки распределения EDA являются стохастическими популяционными алгоритмами, которые исследуют пространство поиска с помощью построения и использования модели распределения вероятностей в явном виде. Стоит отметить, что ЭА и ГА тоже накапливают и обрабатывают некоторую статистическую информацию по результатам прошлых этапов поиска, но такая информация не представлена явно и содержится в хромосомах текущей популяции. Алгоритмы EDA могут быть использованы для усиления стандартных поисковых методов. В частности, есть примеры использования гибридных EDA-ЭА-алгоритмов для вещественных LSGO-задач [6; 7].
Для оценки эффективности и сравнения эффективности подходов к решению задач глобальной оптимизации высокой размерности были разработаны специальные тестовые задачи, которые приняты мировым научным сообществом как сложные. Эти функции, в частности, используются на соревновании методов LSGO-оптимизации, проводимом ежегодно с 2008 года в рамках Международного конгресса по эволюционным вычислениям (IEEE Congress on Evolutionary Computation, CEC). Анализ последних соревнований показал, что большинство методов, продемонстрировавших высокую эффективность, используют динамическую случайную группировку и вещественные поисковые алгоритмы.
Декомпозиция на основе EDA-алгоритма. Основная идея декомпозиции в LSGO-задачах состоит в разбиении задачи на подзадачи меньшей размерности, содержащие одну или несколько переменных. Выбранная часть переменных участвует в поиске оптимального решения, оставшиеся переменные фиксируются, их значения определяются в соответствии с некоторой стратегией (например, используются значения лучшего найденного решения). Очевидно, что лучшие результаты можно получить для полностью сепарабельных задач оптимизации. В случае несепарабельных и частично сепарабельных задач выбор стратегии декомпозиции определяет общую эффективность поискового алгоритма.
В данной работе сформулированы следующие требования к методу декомпозиции:
-
- группировка генов в ГА должна быть динамической для реализации стратегии «исследование и использование» (exploration and exploitation);
-
- группировка должна быть случайной, чтобы избежать «жадного» поиска и локальной сходимости;
-
- группировка должна основываться на результатах прошлых этапов поиска всей популяцией, чтобы обеспечить глобальный поиск;
-
- группировка должна быть адаптивно масштабируемой, чтобы обеспечить эффективную декомпозицию на любой стадии поиска.
Как известно, ГА не собирают статистическую информацию по прошлым этапам поиска в явном виде, но такая информация содержится в хромосомах индивидов в популяции. Один из способов представить эту статистику в явном виде заключается в оценке распределения вероятностей значений компонент бинарного вектора решений как в бинарных EDA-алгоритмах. Такое распределение имеет вид вектора вероятностей появления единичных значений в соответствующих позициях векторов решений:
P ( t ) = ( Р 1 ( t ), Р 2 ( t ), ..., P n ( t ) ) , P i ( t ) =
1 N
= P ( x i = 1) = t;Z x ,1 = 1, n , N j - i
где t – номер текущей популяции; p – вероятность появления значения, равного единице, в -й позиции хромосом индивидов (в анализируемой популяции); x j – значение -го гена у j -го индивида; n – длина хромосомы; N – размер популяции.
Распределение вероятностей в t -м поколении описывает накопленную ГА статистику по результатам прошлых этапов поиска. Мы также можем проанализировать динамику изменения распределения в течение прошлых поколений. В [8] предложен способ анализа и использования динамики компонент вектора вероятностей (1) в бинарных ЭА и EDA. В частности, по анализу динамики компонент можно построить прогноз значений компонент вектора решений, к которым должен сойтись алгоритм. Численные эксперименты показали, что для ГА, который с высокой надежностью находит точку глобального оптимума, компоненты вектора вероятностей сходятся к значению «один», если соответствующая компонента глобального оптимума содержит единицу, и к сходится нулю – в противном случае.
Мы может использовать это свойство для определения генов в хромосоме, которые стоит зафиксировать на этапе группировки (декомпозиции задачи). Будем фиксировать ген в -й позиции на t -й итерации по следующему правилу (2) на основе значений компонент вектора вероятностей (1):
f 0, если pi (t) < (0,5 - 8), x{ (t) = < random, если pi (t) e (0,5 -8,0,5 + 8), (2) [ 1, pi(t) > (0,5 + 8), где 8 - пороговое значение (уровень доверия), 8 e (0,0,5).
Рассмотрим данное правило на примере (рис. 1). На рис. 1 представлен график изменения случайно выбранной компоненты вектора вероятностей во время одного из запусков ГА на функции Растригина. Для выбранного гена значение в точке глобального оптимума равно нулю. Как видно из рис. 1, ГА начинает со случайного равномерного распределения решений в пространстве поиска, поэтому значение вероятности появления единицы в данной позиции равно 0,5. На ранних этапах поиска ГА активно исследует ландшафт целевой функции, потому распределение единиц и нулей в популяции примерно одинаковое, и значение вероятности колеблется около 0,5. После этого ГА локализует перспективный регион пространства поиска и начинает чаще генерировать нули в текущей позиции, вероятность начинает меняться в сторону нуля. Пороговый уровень доверия определяет зону значений вероятностей около 0,5, когда мы не можем однозначно определить, какое значение гена чаще генерирует алгоритм.
Несмотря на то, что мы рассматриваем компоненты распределения по отдельности, ГА анализирует и генерирует решения, учитывая информацию о задаче в целом. Поэтому правило (2) может быть использовано для произвольных, а не только для сепарабельных проблем. Исключением могут быть только десептив-ные задачи (функции-«ловушки»), которые специально конструируются так, чтобы алгоритм на протяжении всего процесса поиска сходился в точку, далекую от глобального оптимума.
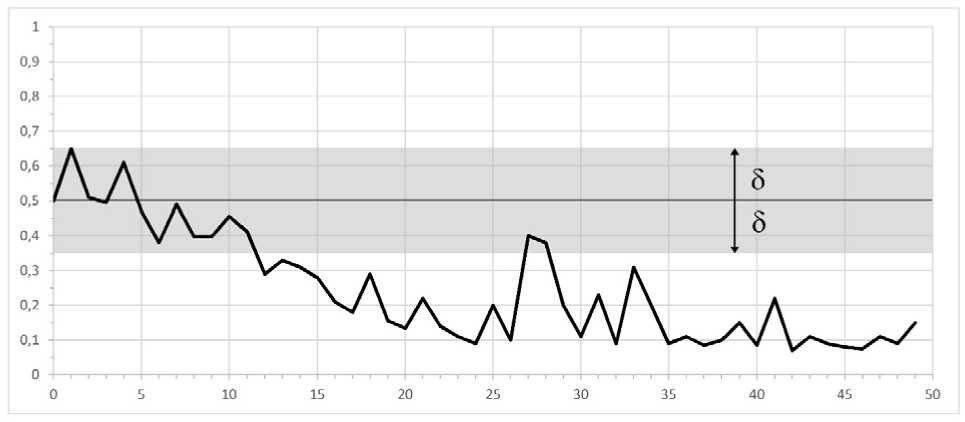
Рис. 1. График изменения компоненты распределения (горизонтальная ось – номер поколения, вертикальная ось – значение вероятности)
Далее мы должны определить количество переменных, которые будут зафиксированы. Существуют разные стратегии. Наиболее популярный подход – разделение пополам, когда для задачи с n переменными фиксируются ровно n /2 компонент. В общем случае мы определим число компонент, которые фиксируются как процент от длины хромосомы, и обозначим α. Параметр α может быть фиксированным или меняться в процессе работы алгоритма. Выбранные переменные и соответствующие значения вектора вероятностей остаются неизменными на протяжении заданного числа поколений – периода адаптации; обозначим его как t adapt . Список зафиксированных компонент определяется случайно. В данной работе мы будем использовать предварительно заданные постоянные значения параметров α и t adapt .
Одним из преимуществ такой декомпозиции является то, что мы не теряем ранее накопленную статистику о поиске при фиксации компонент, так как мы также фиксируем компоненты вектора вероятностей. ГА решает задачу оптимизации в уменьшенном пространстве поиска и обновляет только незафиксированные компоненты распределения. По завершении каждого периода адаптации мы случайным образом фиксируем новые компоненты. В случае, если ранее зафиксированная компонента не будет выбрана, обновление соответствующей ей компоненты распределения продолжится с сохранённого значения.
ГА с декомпозицией на основе EDA-алгоритма для LSGO-задач. Опишем предложенный подход для решения задач глобальной оптимизации большой размерности в деталях.
Вначале мы должны выбрать способ бинарного представления решений исходной задачи оптимизации. Можно использовать стандартный бинарный, Грей-код или любой другой. В результате кодирования мы определяем длину хромосомы (бинарного вектора) n .
Далее необходимо задать значения параметров алгоритмов декомпозиции и ГА, а также максимальное число вычислений целевой функции (MaxFE) или максимальное число поколений (MaxGEN). Критерии MaxFE и MaxGEN можно заменить на любой другой критерий останова.
Полное описание алгоритма можно представить в виде псевдокода (рис. 2).
Островная модель с самоконфигурацией . Многие алгоритмы для LSGO-задач используют группировку компонент на основе кооперативной коэволюции. В этом случае создаются несколько популяций, в которых осуществляются различные группировки компонент. Кооперация осуществляется в момент вычисления пригодности для определения значений фиксированных компонент, например, на основе лучших найденных решений из других популяций.
В данной работе мы также будем использовать несколько популяций, определенных следующим образом. При выполнении основного цикла предложенного алгоритма общая популяция размера N делится на K подпопуляций размера M, где N = K · M . Шаги декомпозиции и работы ГА выполняются для каждой подпопуляции независимо. Каждая подпопуляция может быть рассмотрена как остров (в терминах островной модели ГА) со своей стратегией декомпозиции. После завершения этапа адаптации все индивиды со всех подпопуляций собираются обратно в общую популяцию для обновления общей статистики поиска. Последнее можно рассматривать как кооперацию, так как в дальнейшем каждая подпопуляция будет использовать эту статистику на своем острове. Известно, что островная модель может превосходить по эффективности обычный ГА с одной популяцией [9]. Также мы можем сократить время работы алгоритма в случае использования параллельных вычислений на многоядерном или многопроцессорном компьютере.
Мы можем внести дополнительное взаимодействие подпопуляций в островной модели, используя концепцию, предложенную в [10]. Будем увеличивать размер острова, который демонстрирует большую эффективность решения задачи. С помощью операции миграции лучших индивидов позиции островов будут уравниваться.
Входные данные : n , N , а, 8 , t adapt , MaxFE , параметры операций ГА.
Инициализация:
Случайно сгенерировать популяцию N индивидов длины n .
Рассчитать P(0) по формуле (1).
Основной цикл алгоритма:
Пока не достигнуто MaxFE :
-
1. Этап декомпозиции : Начать новый период адаптации. Зафиксировать случайные а генов в хромосомах и в векторе вероятностей.
-
2. Этап оптимизации выбранных компонент : Выполнять ГА в течение tadapt поколений:
-
а. Вычисление пригодности. Установить значения генов в зафиксированных позициях согласно значению P(t), используя формулу (2).
-
б. Выполнить операции селекции, рекомбинации и мутации.
-
в. Создать новое поколение, обновить значения P(t) вектора вероятностей для активных компонент.
Выходные данные: лучшее найденное решение.
-
Рис. 2. Схема предложенного алгоритма
Поскольку LSGO-задачи весьма затратны в вычислительном плане, выбор оптимальных параметров ГА путем многократного запуска ГА с различными комбинациями параметров невозможен. Мы будем использовать следующую известную схему самокон-фигрурации ГА. Вначале мы определяем список возможных генетических операторов ГА: типы селекции, типы рекомбинации и уровни интенсивности мутации. Для каждой операции определяется вероятность ее применения при формировании нового индивида. Все вероятности инициализируются равными значениями. В процессе работы ГА определяются те операторы, которые в среднем дают большее улучшение пригодности индивидов, значения их вероятностей увеличиваются за счет уменьшения вероятностей менее успешных операторов. Более детальная информация о данной самоконфигурации может быть найдена в [11].
Результаты численных экспериментов. Для оценки эффективности предложенного подхода были использованы 15 тестовых задач большой размерности, представленные на специальной сессии и соревновании по LSGO-оптимизации в рамках Международного конгресса CEC 2013 [12]. Эти задачи обладают различными свойствами практических задач оптимизации большой размерности и являются сложными для многих алгоритмов, а потому могут быть использованы для сравнения специальных алгоритмов для LSGO-задач. Среди них:
-
- 3 полностью сепарабельных задачи (обозначены как f 1 –f 3);
-
- 8 частично сепарабельных задач ( f 4– f 7 с сепарабельными подзадачами, f 8 –f 11 без сепарабельных подзадач);
-
- 3 задачи с взаимовлияющими подзадачами ( f 12– f 14);
-
- 1 полностью несепарабельная задача ( f 15).
Для проведения численных экспериментов использовались следующие настройки (согласно правилам соревнования CEC’13):
-
- размерность всех задач D = 1000;
-
- используется стандартное кодирование с точностью: ε = 0,1 для f 1, f 4, f 7, f 8 и f 11–15, ε = 0,05 для f 3, f 6 и f 10, ε = 0,01 для f 2, f 5 и f 9;
-
- для каждой задачи вычисляется лучшее найденное решение (Best), математическое ожидание (Mean) и стандартное отклонение (StDev) по 25 независимым запускам алгоритма;
-
- максимальное число вычислений целевой функции MaxFE = 3,0·106;
-
- оценка эффективности осуществляется после достижения чисел вычислений целевой функции, равных 1,2·105, 6,0·105 и 3,0·106.
Параметры ГА и EDA-алгоритма следующие:
-
- размер популяции N = 1000 для версии с одной популяцией, N = 500 для островной модели с 3 островами и N = 400 для 5 островов;
-
- период адаптации t adapt = 100;
-
- пороговый уровень доверия δ = 0,05, 0,15 и 0,25;
-
- число фиксированных компонент α = 25, 50 и 75 % длины хромосомы.
Предложенные алгоритмы реализованы в Visual Studio C++ с использованием OpenMP распараллеливания вычислений на многопроцессорных компьютерах. Исходные коды задач на языке C++ взяты из репозитория [13].
К сожалению, даже в случае распараллеливания вычислений каждый запуск алгоритма на одной из задач требует больших временных затрат, а потому многократное решение задач с целью получения статистически значимых выводов об эффективности алгоритма с разными настройками весьма затруднительно при разумных временных ограничениях. Тем не менее, был проведен «грубый» анализ влияния параметров α и δ на эффективность работы алгоритма. Результаты для ГА с одной популяцией и островной модели с 5 островами представлены в табл. 1 и 2. Как видно, островная модель превосходит ГА с одной популяцией почти во всех случаях.
Мы также представили на графиках зависимость лучшего найденного значения от комбинации параметров α и δ. Лучшее найденное значение нормализовано в интервале [0, 1] и усреднено по всем задачам из набора. Графики для 3 значений MaxFE представлены на рис. 3 и 4. Из графиков видно, что лучшие результаты достигаются при больших значениях процента фиксированных компонент. В случае одной популяции, лучшая комбинация ( α = 50 %, δ = 0,15) для MaxFE = 1,2·105, которая смещается к ( α = 50 %, δ = 0,25) для MaxFE = 6,0·105 и MaxFE = 3,0·106. В случае островной модели, лучшие комбинации ( α = 75 %, δ = 0,25) для MaxFE = 1,2·105и ( α = 75 %, δ = 0,15) для MaxFE = 6,0·105и MaxFE = 3,0·106. Можно предположить, что алгоритму требуются разные комбинации параметров на разных этапах поиска. В следующих работах будет предпринята попытка разработать адаптивную схему настройки данных параметров.
Результаты экспериментов для лучших найденных значений параметров представлены в табл. 3.
Результаты предложенного подхода сравнены с другими алгоритмами, которые участвовали в соревновании CEC’13: DECC-G (кооперативная коэволюция со случайной динамической группировкой на базе дифференциальной эволюции) [3], VMO-DE (оптимизация по изменяющейся решетке с помощью дифференциальной эволюции) [14], CC-CMA-ES (эволюционная стратегия адаптации ковариационной матрицы с использованием кооперативной коэволюции) [4], MOS (гибридный алгоритм генерации множества потомков) [15] и SACC (кооперативная коэволюция на основе сглаживания и вспомогательных функций) [16].
В табл. 4 представлены результаты усреднения показателей эффективности алгоритмов по всем задачам, алгоритмы проранжированы по значениям лучшего найденного и математического ожидания. Из табл. 4 видно, что предложенный алгоритм (обозначен как EDA-GA) занял 4-е место по критерию Best и 5-е – по критерию Mean. Стоит отметить, что остальные алгоритмы специально разработаны для задач с вещественными переменными, а предложенный подход является универсальным, так как кодирует переменные в любых шкалах в бинарные. Декомпозиция на основе EDA не использует никакие предположения о свойствах непрерывного пространства поиска. Более того, после бинаризации размерность числа компонент увеличивается по сравнению с исходным непрерывным пространством, так как сложность задачи возрастает. Тем не менее, ГА на основе EDA-декомпозиции превосходит CC-CMA-ES по двум показателям и DECC-G по показателю Best.
Таблица 1
Результаты на задаче f 1 для ГА с одной популяцией
|
α |
25 |
25 |
25 |
50 |
50 |
50 |
75 |
75 |
75 |
|
|
δ |
0,05 |
0,15 |
0,25 |
0,05 |
0,15 |
0,25 |
0,05 |
0,15 |
0,25 |
|
|
1,2·105 |
Best |
2,08·107 |
1,98·107 |
1,72·107 |
1,89·107 |
1,50·107 |
1,59·107 |
1,98·107 |
1,53·107 |
1,76·107 |
|
Mean |
6,13·107 |
5,97·107 |
6,81·107 |
8,95·107 |
4,98·108 |
7,32·107 |
8,30·107 |
8,72·107 |
7,23·107 |
|
|
StDev |
3,31·107 |
2,90·107 |
2,70·107 |
3,74·107 |
2,98·107 |
3,51·107 |
3,66·107 |
3,93·107 |
3,34·107 |
|
|
6,0·105 |
Best |
1,99·103 |
2,11·103 |
1,71·103 |
2,55·104 |
8,23·103 |
1,50·103 |
1,23·104 |
9,20·103 |
9,00·103 |
|
Mean |
2,71·104 |
2,53·104 |
2,22·104 |
3,47·104 |
2,19·104 |
1,99·104 |
3,88·104 |
2,51·104 |
3,02·104 |
|
|
StDev |
9,47·103 |
9,36·103 |
7,90·103 |
1,85·104 |
1,68·103 |
7,08·103 |
1,85·104 |
1,20·104 |
1,69·104 |
|
|
3,0·106 |
Best |
9,32·10-5 |
8,02·10-5 |
7,63·10-5 |
4,50·10-5 |
4,59·10-5 |
7,11·10-5 |
6,73·10-5 |
5,19·10-5 |
6,34·10-5 |
|
Mean |
4,00·10-4 |
4,23·10-4 |
4,51·10-4 |
5,01·10-4 |
5,68·10-4 |
4,98·10-4 |
4,02·10-4 |
3,80·10-4 |
3,56·10-4 |
|
|
StDev |
2,24·10-4 |
2,09·10-4 |
2,19·10-4 |
2,08·10-4 |
4,29·10-4 |
2,11·10-4 |
1,95·10-4 |
1,65·10-4 |
1,82·10-4 |
Таблица 2
Результаты на задаче f 1 для островного ГА c 5 островами
|
α |
25 |
25 |
25 |
50 |
50 |
50 |
75 |
75 |
75 |
|
|
δ |
0,05 |
0,15 |
0,25 |
0,05 |
0,15 |
0,25 |
0,05 |
0,15 |
0,25 |
|
|
1,2·105 |
Best |
1,76·107 |
1,79·107 |
1,73·107 |
1,62·107 |
1,56·107 |
1,63·107 |
1,62·107 |
1,42·107 |
1,45·107 |
|
Mean |
4,90·107 |
4,95·107 |
5,61·107 |
5,72·107 |
5,34·107 |
5,39·107 |
6,16·107 |
5,50·107 |
5,23·107 |
|
|
StDev |
3,04·107 |
3,01·107 |
2,23·107 |
3,15·107 |
2,98·107 |
2,12·107 |
2,41·107 |
2,98·107 |
2,44·107 |
|
|
6,0·105 |
Best |
8,68·103 |
8,61·103 |
8,41·103 |
7,72·103 |
7,58·103 |
7,65·103 |
8,50·103 |
7,00·103 |
6,89·103 |
|
Mean |
1,85·104 |
1,79·104 |
2,07·104 |
2,17·104 |
2,15·104 |
1,77·104 |
1,81·104 |
2,21·104 |
1,99·104 |
|
|
StDev |
8,60·103 |
9,33·103 |
1,07·104 |
1,28·104 |
1,68·103 |
8,12·103 |
1,18·104 |
9,19·103 |
1,68·103 |
|
|
3,0·106 |
Best |
5,78·10-5 |
5,92·10-5 |
5,46·10-5 |
5,09·10-5 |
5,00·10-5 |
4,91·10-5 |
5,47·10-5 |
4,59·10-5 |
4,95·10-5 |
|
Mean |
6,13·10-4 |
5,45·10-4 |
5,17·10-4 |
5,51·10-4 |
5,06·10-4 |
5,40·10-4 |
5,98·10-4 |
5,68·10-4 |
5,44·10-4 |
|
|
StDev |
2,47·10-4 |
2,37·10-4 |
2,19·10-4 |
2,24·10-4 |
4,29·10-4 |
2,21·10-4 |
2,40·10-4 |
4,29·10-4 |
2,22·10-4 |
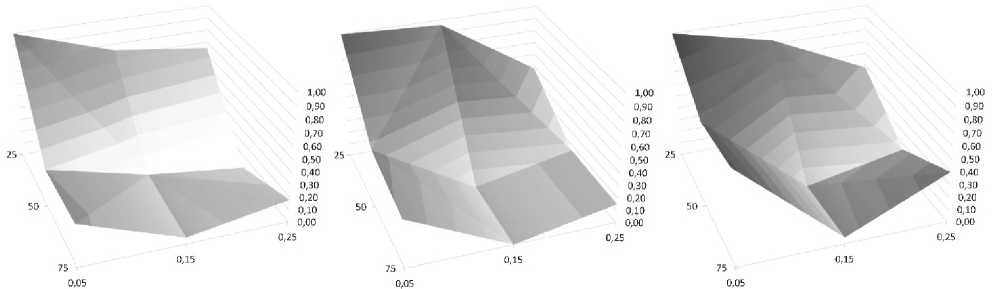
Рис. 3. Зависимость эффективности ГА с одной популяцией от параметров α и δ для MaxFE = {1,2·105, 6,0·105, 3,0·106}
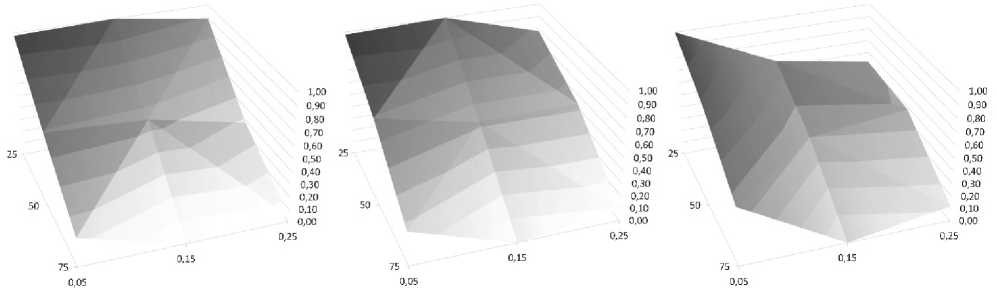
Рис. 4. Зависимость эффективности островного ГА с 5 островами от параметров α и δ для MaxFE = {1,2·105, 6,0·105, 3,0·106}
Таблица 3
Результаты решения тестовых задач островным ГА c 5 островами α = 75 % и δ = 0,15
|
f 1 |
f 2 |
f 3 |
f 4 |
f 5 |
f 6 |
f 7 |
f 8 |
||
|
1,2·105 |
Best |
1,42·107 |
9,63·103 |
1,08·102 |
1,39·1011 |
6,11·1014 |
2,90·105 |
7,05·108 |
3,97·1015 |
|
Mean |
5,50·107 |
1,06·104 |
4,52·101 |
9,15·1011 |
7,17·1014 |
7,78·105 |
2,76·109 |
2,71·1016 |
|
|
StDev |
2,98·107 |
1,53·103 |
1,44·101 |
5,63·1011 |
7,45·108 |
2,61·105 |
1,44·109 |
6,77·1015 |
|
|
6,0·105 |
Best |
6,89·103 |
9,11·103 |
3,04·100 |
1,95·1010 |
3,07·1014 |
5,21·105 |
2,01·108 |
2,09·1014 |
|
Mean |
1,99·104 |
1,25·104 |
1,30·101 |
9,07·1010 |
5,03·1014 |
6,05·105 |
9,41·108 |
2,18·1015 |
|
|
StDev |
1,68·103 |
1,18·103 |
6,32·10-1 |
6,03·1010 |
2,50·107 |
2,60·105 |
7,56·108 |
1,52·1015 |
|
|
3,0·106 |
Best |
4,59·10-5 |
1,82·103 |
2,94·10-5 |
6,60·109 |
7,59·1014 |
6,25·104 |
7,65·107 |
4,49·1013 |
|
Mean |
5,68·10-4 |
3,34·103 |
4,81·10-1 |
2,32·1010 |
9,75·1014 |
4,75·105 |
2,53·108 |
3,64·1014 |
|
|
StDev |
4,29·10-4 |
2,54·102 |
2,28·10-1 |
1,14·1010 |
2,18·106 |
3,35·105 |
8,35·107 |
5,21·1014 |
|
|
f9 |
f10 |
f11 |
f12 |
f13 |
f14 |
f15 |
Average |
||
|
1,2·105 |
Best |
1,08·109 |
8,87·106 |
1,46·1011 |
3,87·106 |
2,66·1010 |
1,88·1011 |
3,61·107 |
3,05·1014 |
|
Mean |
1,80·109 |
7,14·107 |
3,47·1011 |
4,36·108 |
2,98·1010 |
5,78·1011 |
2,69·108 |
1,85·1015 |
|
|
StDev |
4,27·108 |
1,57·107 |
2,25·1011 |
7,89·108 |
1,12·1010 |
3,67·1011 |
9,91·107 |
4,52·1014 |
|
|
6,0·105 |
Best |
6,42·108 |
7,91·106 |
1,34·1010 |
2,40·103 |
6,28·109 |
5,68·1010 |
1,80·107 |
3,44·1013 |
|
Mean |
1,25·109 |
1,38·107 |
9,84·1010 |
6,66·103 |
1,47·1010 |
1,03·1011 |
2,43·107 |
1,79·1014 |
|
|
StDev |
5,21·108 |
1,65·107 |
1,18·1011 |
5,53·103 |
4,83·109 |
6,70·1010 |
8,68·106 |
1,02·1014 |
|
|
3,0·106 |
Best |
4,15·108 |
6,18·106 |
2,60·1010 |
7,72·102 |
8,02·109 |
1,42·1010 |
2,40·107 |
5,36·1013 |
|
Mean |
8,06·108 |
1,61·107 |
7,01·1010 |
2,30·103 |
1,27·1010 |
1,69·1011 |
3,05·107 |
8,93·1013 |
|
|
StDev |
1,72·108 |
7,89·106 |
4,29·1010 |
2,41·103 |
2,96·109 |
4,81·1010 |
5,13·106 |
3,47·1013 |
Таблица 4
Сравнение LSGO-подходов
|
Алгоритм |
SACC |
MOS |
VMO-DE |
DECC-G |
CC-CMA-ES |
EDA-GA |
|
Best |
9,80·1012 |
2,17·1011 |
4,90·1013 |
5,80·1013 |
6,25·1013 |
5,36·1013 |
|
Ранжирование по значению Best |
2 |
1 |
3 |
5 |
6 |
4 |
|
Mean/ |
8,0·1013/ |
5,33·1011/ |
5,32·1013/ |
7,7·1013/ |
8,58·1013/ |
8,93·1013/ |
|
StDev |
5,08·1013 |
2,04·1011 |
4,81·1012 |
1,02·1013 |
2,39·1013 |
3,47·1013 |
|
Ранжирование по значению Mean |
4 |
1 |
2 |
3 |
6 |
5 |
Полученные результаты позволяют сделать предположение, что предложенный подход будет эффективен при решении практических задач глобальной оптимизации большой размерности, в которых представлены переменные в произвольных шкалах (включая смешанные). В дальнейших исследованиях мы сконцентрируемся на повышении эффективности подхода путем анализа его структуры и значений управляемых параметров. В частности, стоит ввести адаптацию параметров α и δ на основе анализа сходимости компонент вектора вероятностей.
Заключение. В работе предложен новый подход для решения сложных задач глобальной оптимизации высокой размерности с помощью бинарного ГА с EDA-декомпозицией. Алгоритм EDA используется для сбора и анализа статистики о прошлых этапах поиска и прогноза сходимости компонент решения для снижения размерности задачи. В работе сравнивается стандартная модель ГА с одной популяцией и островная модель, которая продемонстрировала большую эффективность. Предложенный подход уступает в эффективности некоторым известным подходам, но в целом показатели эффективности имеют сравнимые значения. Преимуществом подхода является то, что он позволяет решать задачи с любым представлением решений и не требует какой-либо априорной информации о пространстве поиска.
Acknowledgments. This research was supported by the President of the Russian Federation grant (MK-3285.2015.9) and by Russian Foundation for Basic Research and Krasnoyarsk Regional Fund for Support of Scientific and Technical Activities (project 16-41-240822).
Список литературы Бинарный генетический алгоритм с декомпозицией на основе оценки распределения для задач глобальной оптимизации высокой размерности
- Mahdavi S., Shiri M. E., Rahnamayan Sh. Metaheuristics in large-scale global continues optimization: A survey. Information Sciences. 2015, Vol. 295, P. 407-428.
- Potter M., De Jong K. A. Cooperative coevolution: an architecture for evolving coadapted subcomponents. Evol. Comput. 2000, No. 8 (1), P. 1-29.
- Yang Zh., Tang K., Yao X. Large scale evolutionary optimization using cooperative coevolution. Inform. Sci. 2008, No. 178 (15), P. 2985-2999.
- Liu J., Tang K. Scaling up covariance matrix adaptation evolution strategy using cooperative coevolution. In Intelligent Data Engineering and Automated Learning -IDEAL. 2013, P. 350-357.
- Omidvar M. N., Li X., Mei Y., Yao X. Cooperative co-evolution with differential grouping for large scale optimization. IEEE Trans. Evol. Comput. 2014, No. 18 (3), P. 378-393.
- Dong W., Chen T., Tino P., Yao X. Scaling up estimation of distribution algorithms for continuous optimization. IEEE Trans. Evol. Comput. 2013, No. 17 (6), P. 797-822.
- Wang Y., Li B. A restart univariate estimation of distribution algorithm: sampling under mixed gaussian and lévy probability distribution. In IEEE Congress on Evolutionary Computation, CEC 2008 (IEEE World Congress on Computational Intelligence). 2008, P. 3917-3924.
- Sopov E., Sopov S. The convergence prediction method for genetic and PBIL-like algorithms with binary representation. In IEEE International Siberian Conference on Control and Communications (SIBCON 2011). 2011, P. 203-206.
- Gonga Y.-J., Chena W.N., Zhana Zh.-H., Zhanga J., Li Y., Zhange Q., Lif J.-J. Distributed evolutionary algorithms and their models: A survey of the state-of-the-art. Applied Soft Computing. 2015, No. 34, P. 286-300.
- Sopov E. A Self-configuring Metaheuristic for Control of Multi-Strategy Evolutionary Search. ICSI-CCI 2015, Part III, LNCS 9142, 2015, P. 29-37.
- Semenkin E. S., Semenkina M. E. Self-configuring Genetic Algorithm with Modified Uniform Crossover Operator. Advances in Swarm Intelligence //Lecture Notes in Computer Science 7331. Springer-Verlag, Berlin Heidelberg, 2012, P. 414-421.
- Li X., Tang K., Omidvar M.N., Yang Zh., Qin K. Benchmark functions for the CEC 2013 special session and competition on large-scale global optimization. Technical Report, Evolutionary Computation and Machine Learning Group, RMIT University, Australia, 2013.
- Test suite for the IEEE CEC'13 competition on the LSGO. Available at: http://goanna.cs.rmit.edu.au/~xiaodong/cec13-lsgo/competition/lsgo_2013_benchmarks.zip.
- Li X., Tang K., Omidvar M. N., Yang Zh., Qin K. Technical report on 2013 IEEE Congress on Evolutionary Computation Competition on Large Scale Global Optimization. Available at: http://goanna.cs.rmit.edu.au/~xiaodong/cec13-lsgo/competition/lsgo-competition-sumary-2013.pdf.
- LaTorre A., Muelas S., Pena J.-M. Large scale global optimization: experimental results with MOS-based hybrid algorithms. In 2013 IEEE Congress on Evolutionary Computation (CEC). 2013, P. 2742-2749.
- Wei F., Wang Y., Huo Y. Smoothing and auxiliary functions based cooperative coevolution for global optimization. In 2013 IEEE Congress on Evolutionary Computation (CEC). 2013, P. 2736-2741.


