Биофизические особенности сосудистого русла высокого давления как системы с распределенными параметрами
Автор: Аксенов В.В.
Журнал: Человек. Спорт. Медицина @hsm-susu
Рубрика: Теория функциональных систем и современные проблемы стресса, адаптации и поведения
Статья в выпуске: 4 (44) т.1, 2005 года.
Бесплатный доступ
Предложена математическая модель сосудистого русла высокого давления. Выявлен закон ветвления сосудов: волновая проводимость стволового сосуда равна сумме волновых проводимостей ответвляющихся сосудов. Табулированы геометрические и гидродинамические характеристики сосудов человека.
Короткий адрес: https://sciup.org/147152032
IDR: 147152032
Текст научной статьи Биофизические особенности сосудистого русла высокого давления как системы с распределенными параметрами
Предложена математическая модель сосудистого русла высокого давления. Выявлен закон ветвления сосудов: волновая проводимость стволового сосуда равна сумме волновых проводимостей ответвляющихся сосудов. Табулированы геометрические и гидродинамические характеристики сосудов человека.
Большинство разработанных моделей описывают сосудистое русло высокого давления как систему с сосредоточенными параметрами [2, 5, 6, 8, 9, И, 12]. Это связано не только со сложностью сосудистого русла как системы, но и с отсутствием количественных характеристик (радиус, толщина стенки, модуль упругости и др.) большого множества эластических и мышечно-эластических сосудов, закономерности их ветвления, индивидуальной вариабельностью параметров сосудов и их количества, простотой математического аппарата [4]. Работы по изучению сосудистого русла как системы с распределенными параметрами немногочисленны [3,10].
Изучение скорости распространения пульсовых волн позволяет оценить модуль упругости стенки сосуда, тип сосуда (эластический, мышечно-эластический или мышечный). Отражение пульсовых волн есть одна из главных причин изменения их формы в артериях. Измерение импеданса позволяют судить о строении сосудистого русла ниже точки измерения.
Однако многие вопросы гемодинамики сосудистого русла остаются не изученными. Не исследованы закономерности строения архитектоники сосудистого русла [1]. Не известно, как осуществляется согласование выходных характеристик сердца с входными характеристиками сосудистого русла, фрагментов сосудистого русла между собой и сосудистого русла высокого давления с резистивным сосудистым руслом. Всё ещё остается открытым вопрос о физиологической значимости пульсирующего течения крови. Не выявлена клиническая значимость пульсовых явлений в артериальной системе. Не изучены частотные характеристики сосудистого русла и влияние его на колебательные процессы ЧСС и ударного объема сердца.
Целью исследования явилось моделирование сосудистого русла высокого давления как системы с распределенными параметрами.
Задачами исследования были:
-
1. Поиск в литературе, расчет и табуляция в таблицы параметров сосудов высокого давления.
-
2. Разработка модели сосудистого русла как системы с распределенными параметрами.
-
3. Выявление закономерностей строения архитектоники сосудистого русла высокого давления.
Необходимостью рассмотрения сосудов высокого давления как гемодинамической цепи с распределенными параметрами является сравнимость интервала времени распространения по нему пульсовой волны с интервалами времени значимого изменения артериального давления и кровотока [7]. Экспериментально установлено, что скорость распространения пульсовой волны в сосудистом русле изменяется в пределах 3-5 м/с. Следовательно, пульсовая волна пройдет сосуд длиной 10 см в течение 0,1 с, что соизмеримо со временем систолы (0,3 с).
Будем считать, что параметры сосуда (радиус, толщина стенки, модуль упругости и др.) распределены равномерно вдоль его длины, т. е. он представляет собой однородную гемодинамическую цепь. Течение крови в таком сосуде описывается дифференциальными уравнениями в частых производных:
дх dt
_®О_=с—.
дх dt
Т№К=%лг11хг - вязкостное сопротивление на единицу длины сосуда; L = р/8 - инерционная индуктивность на единицу длины сосуда; С = 3rS/2Eh - гемодинамическая емкость на единицу длины сосуда, Р - давление, Q - объемная скорость кровотока, 77 - коэффициент вязкости крови, S - просвет сосуда, р - плотность крови, г -^asstjc, сосуда, h - толщина стенки сосуда, Е - эффективный модуль упругости стенки сосуда.
При установившемся режиме кровотока по сосуду давление и объемная скорость в крови изменяются по периодическому закону. Представив периодические функции времени в ряд Фурье, можно произвести расчет отдельно для каждой синусоидальной составляющей этого ряда и вследствие линейности гемодинамической цепи результирующий процесс получим, пользуясь методом наложения. Поэтому достаточно произвести анализ процессов в сосуде при синусоидальных давлениях и скоростях кровотока.
Пользуясь комплексным методом, перепишем уравнения течения крови по сосуду для комплексных значений давления и скорости кровотока:
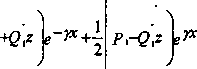
(И)
-^-=RQ + jwLQ' (3)
дх
Используя соотношение
_^ = jwcP (4)
ох
—fe^ +е l^^chyt и Ме^-е ^^shyx , (12)
2k ) 2k )
Комплексы Р и Q являются функциями координаты х (продольная ось сосуда), и, соответственно, уравнения в частных производных для мгновенных значений Р и Q перешли в обыкновенные дифференциальные уравнения для и и Q.
Дифференцируя первое уравнение по Хи используя второе, находим:
получаем:
Р = pxchyx -Q^shp , (13)
2 =Qick)gc -—shyx . (14)
Значения давления Р2 и скорости кровотока Q2 в конце сосуда получаются, если положить X-1:
^=(R4-jwE^jwc)P=yU- (5)
«х где: у = -Jjwc (R + jwL ) = a + jP .
Р 2 = Р iChyl -Q ^sh yl , (15)
Q 2 = Q xch yl - ^-sh yl • (16)
z
Введем обозначения:
Решение уравнения для Р имеет следующий вид:
^Р =Л Л ге” . (6)
P\*Q\Z e"^ «Рф^ =P Из первого уравнения находим Q-. Тогда при y=a+jP имеем где z = R + jwL jwC Комплексные величины у и z являются основными характеристиками однородного сосуда и, соответственно, называются коэффициентом распространения и волновым (характеристическим) сопротивлением, a - коэффициент затухания, 0 -коэффициент фазы. Величины а и /3 всегда больше нуля. Условимся снабжать далее давление и скорость кровотока в начале сосуда (х=0) индексом 1 (Pi, QPи в конце сосуда (х = /, где I - длина сосуда) индексом 2 (Р2, Q2). Для определения произвольных постоянных Aj и А2 достаточно знать две из этих четырех величин. Выразим их через Р] и Qi. Полагая х = 0, имеем: Р, =А.+А2и Q =1(4-А.), (8) А.^Р.+б^, А,^?,^,^. (9) Следовательно, p^x^Q^V^^Pv-qA^ (10) Следовательно, Р =Рф+Рф = Рфе-ах еА^Круб^еА6*^ А(19) Переходя от комплекса Р к изображаемому им давлению Р, получим: Р =Рф + Ру = >^рфе-ах sm^t +§-РхУ + 12 Ру^0® sin^Z+0+Дх) ’ где: Pp-прямая волна, бегущая от начала сосуда к концу, а Ру- обратная волна, бегущая от конца сосуда к его началу. Длина волны Х = 2я1р, а скорость распространения волны(фазовая скорость) V =w / Р. Амплитуда прямой волны затухает по показательному закону с коэффициентом затухания а, а амплитуда обратной волны, наоборот, возрастает по такому же закону. Аналогично, рассматривая скорость кровотока получим: Q=QV*QV, (21) где Q р - прямая волна тока, a Q - обратная волна. Отношение комплекса давления прямой волны к комплексу скорости кровотока прямой волны равно волновому сопротивлению сосуда, а для обратных волн соответствующее отношение равно (-Z): _Р Фг _ 2.2г Рфх 21+21 QVx z+li Q ф Q у Появление обратных волн можно рассматривать как результат отражения прямых волн от конца сосуда. Соответственно, прямые волны называются падающими, а обратные - отраженными. Коэффициентом отражения давления qp от конца линии называют отношение отраженной волны р т 2 При 2) = z2 отражения волн не происходит. Рассматривая мощность W в месте сопряжения сосудов, имеем: к падающей волне р„ давления в конце сосуда. Со ответственно, коэффициентом отражения скорости кровотока qy называется отношение к Q ■ W=PiQx=P2Q2 или V V 21 21 Z1 22 Следовательно, w91=wV)+wVi. (30) Пусть волна фх, бегущая от источника по однородному сосуду, имеющему волновое сопротивление Zb достигла его окончания, в котором он соединен с другим сосудом, имеющим волновое сопротивление Z2. Обозначим давление и скорость кровотока в первом сосуде через Pi и Qb а во втором - через Р2 и Q2. В месте сопряжения обоих сосудов имеем Pi = Р2 и Q] = Q2. Предположим, что во втором сосуде до прихода волны из первого сосуда давления не было. Тогда непосредственно после прихода волны к месту сопряжения сосудов во втором сосуде может возникнуть лишь волна ф^, бегущая в том же направлении, что и волна 1, и называемая преломленной волной, в то время как в первой линии, кроме волны фх, называемой падающей волной, при Z] * Z2 обязательно возникает волна Pi, бегущая в обратном направлении и называемая отраженной волной, т. к. иначе не могут быть удовлетворены условия равенства давлений или скоростей кровотока в месте сопряжения сосудов. Поэтому отмечая индексами b уь ф1 соответственно падающие, отраженные и преломленные волны, в месте сопряжения сосудов имеем: Отсюда следует, что часть мощности падающих волн (и^У равная мощности преломления волн (^), переходит во второй сосуд, а остальная часть, равная мощности отраженных волн (^^Х возвращается обратно в первый сосуд. Таким образом, если происходит отражение волн в месте сопряжения двух сосудов с разными волновыми сопротивлениями, то это энергетически не выгодно. Пусть волна фх, бегущая от источника по однородному сосуду, имеющему волновое сопротивление Z], достигла конца этого сосуда, в котором этот сосуд разветвляется на два других сосуда с волновыми сопротивлениями Zi и Z2. В месте сопряжения трех сосудов имеем Р1 = Рг*Рз и 61=62+63 <31) Отсюда находим: Рх = Рфх+Рф=Рф=Рф=Р1=Рз ’ <32) д_РФГРФ1=^+^Фз=дг+дз . (зз) 21 22 23 Рх = Рф*Рф=Рф=Р^( 1 £ь.е,. 2 1 Из этих выражений имеем: Рфг= ”~Рфх > Рфх= 2’Рфр (25) z Z2+Z1 1 1 Z2+Z1 21+2 2 ^1 2г+21 Отсюда находим коэффициенты отражения (q) и коэффициенты преломления (/): Из этих выражений имеем: Р^Рз+Рз -и ^=62+63 ’ £4) др=^ = УГ2^ РФ1 zo+zl , (35) „ _^V1 _2 1~2 О 6 бфх Zl+zo q =^^ ЧР Zi + Zi =zi-z2 qQ где zo= Z1Z1 - общее сопротивление парал-Z2+Z3 лельно соединенных волновых сопротивлений Z2 и Z3. При ZV=ZQ отражение волн не происходит. В этом случае мощность падающих волн полностью переходит в мощность преломленных волн, что энергетически выгодно. Экспериментально установлено, что в однородном сосуде скорость распространения гармонической пульсовой волны практически не зависит от её частоты [1]. Это возможно, если сопротивление кровотоку обусловлено в основном её инерцией (Ж! » R), что характерно для крупных сосудов. В этом случае параметры однородного сосуда Если R^O, то В табл. 1 представлены геометрические характеристики крупных артериальных сосудов человека (литературные данные). Таблица 1 Геометрические характеристики крупных артериальных сосудов Артерия 1, см г, см h, см S, см2z Аорта, восходящая 4,00 1,450 0,162 6,601850 Дуга 5,90 1,090 0,130 3,730634 Грудная 15,60 0,840 0,087 2,215584 Брюшная 15,90 0,580 0,810 1,056296 Подвздошная, общая 5,80 0,370 0,063 0,429866 Наружная подвздошная 8,30 0,290 0,055 0,264074 Бедренная, общая 18,30 0,290 0,052 0,264074 Глубокая ветвь 6,30 0,186 0,046 0,108631 Подколенная 18,90 0,202 0,047 0,128125 Большеберцовая, задняя 32,10 0,193 0,046 0,116962 Большеберцовая, передняя 34,30 0,130 0,039 0,053066 Плечеголовная 3,40 0,620 0,086 1,207016 Подключичная левая 10,20 0,413 0,070 0,535587 Подмышечная 18,50 0,364 0,062 0,416037 Плечевая 23,50 0,258 0,052 0,209011 Локтевая 23,80 0,197 0,046 0,121860 Лучевая 23,50 0,156 0,042 0,076415 Межкостная ладонная 7,90 0,091 0,028 0,026002 Чревная 1,00 0,390 0,064 0,477594 Желудочная левая 7,10 0,180 0,045 0,101736 Селезеночная 6,30 0,275 0,054 0,237463 Печеночная 6,60 0,226 0,049 0,160379 Почечная (4-5 ветвлен, парная) 6,60 0,260 0,052 0,212264 Брыжеечная верхняя 5,90 0,435 0,069 0,594167 Нижняя брыжеечная 5,00 0,160 0,043 0,0803 84 Сонная общая левая 17,70 0,370 0,063 0,429866 Внутренняя левая сонная 11,80 0,162 0,072 0,082406 Мозга передняя левая 5,90 0,083 0,026 0,021631 Сонная общая правая 16,50 0,37 0,063 0,429866 Позвоночная 14,80 0,186 0,045 0,108631 Аорта, луковица 1,50 1,500 0,162 7,065000 Левая венечная 1,10 0,220 0,040 0,151976 Правая венечная 1,00 0,220 0,040 0,151976 В табл. 2 представлены гидродинамические человека (вычисленные нами по формулам модели характеристики крупных артериальных сосудов сосудистого русла). Таблица 2 Гидродинамические характеристики крупных артериальных сосудов Артерия L, г/см5 R, дин-с/см6 Ср, см2(дин-см 2) Чо-6 Z=(L/C)0’5 Y=l/Z Аорта, восходящая 0,161 0,026 25,320 0,080 12,560 Дуга 0,284 0,081 13,410 0,146 7,569 Грудная 0,478 0,230 9,168 0,228 4,078 Брюшная 1,004 1,013 0,324 1,759 1,508 Подвздошная, общая 2,466 6,117 1,082 1,510 0,662 Наружная подвздошная 4,014 16,210 0,597 2,594 0,386 Бедренная, общая 4,014 16,210 0,631 2,522 0,397 Глубокая ветвь 9,758 95,790 0,188 7,200 0,139 Подколенная 8,273 68,860 0,236 5,921 0,169 Большеберцовая задняя 9,063 82,630 0,210 6,564 0,152 Большеберцовая передняя 19,980 401,400 0,076 16,230 0,062 Плечеголовная 0,878 0,776 3,729 0,485 2,061 Подключичная левая 1,979 3,941 1,354 1,209 0,827 Подмышечная 2,548 6,531 1,047 1,560 0,641 Плечевая 5,072 25,880 0,444 3,378 0,296 Локтевая 8,698 76,120 0,224 6,236 0,160 Лучевая 13,870 193,600 0,122 10,680 0,094 Межкостная ладонная 40,770 167200 0,036 33,550 0,030 Чревная 2,219 4,956 1,247 1,334 0,750 Желудочная левая 10,420 109,200 0,174 7,729 0,129 Селезеночная 4,464 20,050 0,518 2,935 0,341 Печеночная 6,609 43,950 0,317 4,566 0,219 Почечная (4-5 ветвлен., парная) 4,994 25,090 0,455 3,313 0,302 Брыжеечная верхняя 1,784 3,202 1,605 1,054 0,949 Нижняя брыжеечная 13,190 174,900 0,128 10,140 0,099 Сонная общая левая 2,466 6,117 1,082 1,510 0,662 Внутренняя левая сонная 12,860 166,500 0,079 12,720 0,079 Мозга передняя левая 49,000 2416,000 0,030 40,690 0,025 Сонная общая правая 2,466 6,117 1,082 1,510 0,662 Позвоночная 9,758 95,790 0,192 7,121 0,140 Аорта, луковица - 0,150 0,023 28,040 0,073 13,130 Левая венечная 6,975 48,940 0,358 4,413 0,277 Правая венечная 6,975 48,940 0,358 4,413 0,277 В табл. 3 представлен закон ветвления крупных артериальных сосудов человека. Таблица 3 Закон ветвления крупных артериальных сосудов человека Стволовой сосуд Y Сосуды ответвления Y EY Луковица аорты 13,10 Восх. аорт. 0,30 13,10 Лев. венеч. 0,30 Пр. венеч. 12,5 Дуга аорты 7,60 Плечегол ствол 2,00 7,60 Лев. общ. сонная 0,70 Лев. подключили. 0,80 Бронх, и трахеал. ветви 0,10 Грудная аорта 4,00 Брюшная аорта 1,50 Пр.подвзд. 0,70 1,50 Лев. подвз. 0,70 Крестцов. 0,10 Из табл. 3 видно, что волновая проводимость стволового сосуда равна сумме волновых проводимостей ответвляющихся от ствола сосудов. Это предотвращает появление обратных пульсовых волн (к сердцу) давления и кровотока и минимизирует потери энергии кровотока в сосудистой системе. Результаты исследования позволяют сделать следующие выводы: 1. Впервые затабулированы геометрические и гидродинамические характеристики крупных артериальных сосудов человека. 2. Открыт закон ветвления крупных артериальных сосудов человека - волновая проводимость стволового сосуда равна сумме волновых проводимостей ответвляющихся от ствола сосудов, что предотвращает появление обратных пульсовых волн и минимизирует потери энергии кровотока в сосудистой системе.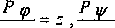
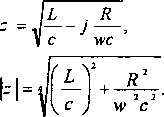
Список литературы Биофизические особенности сосудистого русла высокого давления как системы с распределенными параметрами
- Багаев С.Н., Захаров В.Н., Орлов В.А. Закономерности ветвления кровеносного русла. -Новосибирск: Институт лазерной физики, Препринт № 2, 2000. -60 с.
- Биологическая кибернетика/Под редакцией А.Б. Когана -М.: Высшая школа, 1977. -408 с.
- Биофизика/Ю.А. Владимиров, Д.И. Рощупкин, А.Я. Потапенко, А.И. Деев. -М.: Медицина, 1983. -272 с.
- Гайворонский И.В. Нормальная анатомия человека. -СПб.: СпецЛит, 2000. -Т. 2. -424 с.
- Гайтон А. Физиология кровообращения. -М.: Медицина, 1969. -472 с.
- Моделирование физиологических систем организма/В.И. Шумаков, В.И. Новосельцев, М.П. Сахаров, Е.Ш. Штенгольд. -М.: Медицина, 1971. -352 с.
- Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. -Л.: Энергия, 1967. -T.1. -522 с.
- Основы физиологии человека/Под редакцией В.И. Ткаченко. -СПб., 1994. -Т. 1. -567 с.
- Павловский Ю.Н., Регигер C.A., Скобелева И.М. Гидромеханика крови//Итоги науки. Серия: Механика. Гидромеханика. -М.: Изд-во ВИНИТИ, 1970. -С. 9-96.
- Педли Т. Гидродинамика крупных кровеносных сосудов. -М.: Мир, 1983. -400 с.
- Физиология кровообращения. Физиология сосудистой системы. -Л.: Наука, 1984. -652 с.
- Физиология человека. -М.: Мир, 1986. -Т. 3. -288 с.


