Биоклиматические рамочные модели для климатипов лесных древесных пород

Для ссылок:

Александров, Г. А. Биоклиматические рамочные модели для климатипов лесных древесных пород [Электронный ресурс] / Г. А. Александров, Н. Е. Проказин // Лесохоз. информ. : электрон. сетевой журн. – 2018. – № 1. – С. 90–102. URL:

Географическое распространение древесных пород в значительной степени ограничивается климатическими условиями. Приспособленность к определенным климатическим условиям является результатом или фенотипической пластичности, или генетической адаптации.

Фенотипическая пластичность – способность данного генотипа продуцировать различные фенотипы в зависимости от условий окружающей среды. Фенотипические признаки проявляются в течение жизни одного поколения и, как правило, не наследуются (за исключением тех случаев, когда включается эпигенетический механизм наследования).

Генетическая адаптация происходит путем естественного отбора, в результате которого происходит генетическое разделение вида на экотипы, как результат действия отбора в своеобразных условиях внешней среды и проявления адаптации к этим условиям. Под влиянием климатических факторов возникают климатические экотипы – климатипы [1].

Таким образом, климатип может представлять собой генетически различимую популяцию (совокупность особей одного вида, заселяющих определенную территорию, свободно скрещивающихся друг с другом и в той или иной степени изолированных от других совокупностей [1]), обладающую признаками, благоприятными для адаптации к определенным климатическим условиям (например, к более холодному или к более сухому климату [2–4]), географическое распространение которой ограничено климатическими параметрами за пределами адаптации.

Метод моделирования

Для биоклиматического моделирования распространения лесных древесных пород используют рамочные модели [5–11]. Разработка таких моделей включает следующие этапы: 1) анализ данных о встречаемости изучаемой лесной породы; 2) установление климатических по- казателей, которые влияют на ее встречаемость; 3) определение значений выявленных показателей («рамки»), в пределах которых порода встречается.

Распространение древесных пород, как правило, сдерживается общим недостатком тепла и влаги. О недостатке тепла нередко судят по биотемпературе (BT) [12] – сумме среднемесячных температур выше 0о, но ниже 30 оС, деленной на 12. В зависимости от биотемпературы выделяют 6 зон: полярная, субполярная, бореальная, суббореальная, субтропическая, тропическая. О недостатке влаги судят по коэффициенту увлажнения (MI), который характеризует отношение годового количества осадков к годовой величине испаряемости. На основании значения индекса увлажнения выделяют 8 подзон: супераридная, пераридная, аридная, семиаридная, субгумид-ная, гумидная, пергумидная, супергумидная.

Если в рамках ареала лесной породы климатические условия меняются в широких диапазонах, то есть основания предполагать, что существуют несколько климатипов данной лесной породы, каждый из которых приспособлен к особенностям климатических условий района произрастания. Рамочные модели климатипов, приведенные ниже, предполагают, что популяции лесной породы, произрастающие в разных биомах, могут различаться генетически. Кроме того, подразумевается, что популяции, произрастающие в пределах одного биома, могут различаться по морозостойкости и засухоустойчивости.

Результаты исследований

Распространение древесных пород сдерживается минимальной температурой воздуха и временным дефицитом влаги в жаркое время года. Поэтому в рамочных моделях, предлагаемых ниже, используются такие климатические показатели, как температура самого холодного зимнего месяца и слой осадков самого сухого летнего месяца. Кроме того, используется среднегодовая температура воздуха для выделения клима-типов, произрастающих в зоне вечной мерзлоты, а также некоторые другие показатели климатических условий.

Дуб черешчатый. Распространение дуба че-решчатого сдерживается общим недостатком тепла в северной части его ареала и влаги в южной части, а также длительностью и интенсивностью морозов и засух. Ареал распространения дуба черешчатого не выходит за пределы гумидной и субгумидной подзон суббореальной зоны. В рамках этого ареала климатические показатели меняются в широких дипазонах, что дает основание предположить существование следующих климатипов:

• ✓    Гумидный:

K 1 ={{x,y}:F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅ ⋅θ (T min (x,y)+10) ⋅θ (P min (x,y)-50)

• ✓    Гумидный засухоустойчивый:

K2={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅ ⋅θ (T min (x,y)+10) ⋅θ (P min (x,y)-30) ⋅ ⋅θ (1- θ (P min (x,y)-50))

• ✓    Гумидный морозостойкий:

K 3 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅ ⋅θ (T min (x,y)+17) ⋅θ (P min (x,y)-30) ⋅ ⋅θ (1- θ (T min (x,y)+10))

• ✓    Гумидный морозостойкий засухоустойчивый:

K4={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅

⋅θ (T min (x,y)+17) ⋅θ (P min (x,y)-30) ⋅ θ (1- θ (T min (x,y)+10)) θ (1- θ (P min (x,y)-50)) ✓ Субгумидный:

K 5 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-0.5) ⋅

⋅θ (T min (x,y)+10) ⋅θ (P min (x,y)-50) ⋅ ⋅θ (1- θ (MI(x,y)-1.0))

• ✓    Субгумидный засухоустойчивый:

K 6 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-0.5) ⋅

⋅θ (T min (x,y)+10) ⋅θ (P min (x,y)-30) ⋅ ⋅θ (1- θ (MI(x,y)-1.0)) θ (1- θ (P min (x,y)-50))

• ✓    Субгумидный морозостойкий:

K 7 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-0.5) ⋅

⋅θ (T min (x,y)+17) ⋅θ (P min (x,y)-50) ⋅ ⋅θ (1- θ (MI(x,y)-1.0)) θ (1- θ (T min (x,y)+10)) ✓ Субгумидный морозостойкий засухоус -тойчивый:

K 8 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-0.5) ⋅

⋅θ (T min (x,y)+17) ⋅θ (P min (x,y)-30) ⋅ ⋅θ (1- θ (MI(x,y)-1.0)) θ (1- θ (T min (x,y)+10)) ⋅ ⋅θ (1- θ (P min (x,y)-50))

где:

• x – широта, град.;

• y – долгота, град.;

BT – биотемпература, °С;

MI – индекс увлажнения;

Tmin – температура самого холодного зимнего месяца, °С;

Pmin – слой осадков самого сухого летнего месяца, мм;

• θ – функция Хевисайда:

  θ (z)=

  
  

  θ (0, z < 0 1, z ≥ 0.

  
  

Ель европейская. Распространение ели европейской сдерживается недостатком тепла в северной части ареала и сухостью климата в его южной части. Ель европейская выдерживает морозы до -40 °С. Тем не менее при T_min ниже -15 °С ель европейская сменяется елью сибирской, а при T_min выше -2 °С – лиственными породами. Таким образом, распространение ели европейской сдерживается не только биоклиматическими, но и геоботаническими факторами. На Кавказе ель европейская сменяется елью восточной, несмотря на то что биоклиматические условия этого района мало отличаются от биоклиматических условий местопроизрастания ели европейской.

Климатипы ели европейской могут быть заданы в виде следующей рамочной модели:

• ✓    Суббореальный гумидный:

K1={{x,y}: F(x,y)=1 };

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅ ⋅θ (T min (x,y)+15) ⋅θ (P min (x,y)-40) ⋅ ⋅θ (1- θ (T min (x,y)+2))

• ✓    Бореальный субгумидный:

K 2 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅ ⋅θ (T min (x,y)+15) ⋅θ (P min (x,y)-40) ⋅ ⋅θ (1- θ (BT(x,y)-6)) θ (1- θ (T min (x,y)+2)) ⋅ ⋅θ (1- θ (MI(x,y)-1.0))

• ✓    Бореальный гумидный:

K3={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+15) ⋅θ (P min (x,y)-40) ⋅ ⋅θ (1- θ (BT(x,y)-6)) θ (1- θ (T min (x,y)+2)) ✓ Субполярный гумидный:

K 4 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-1) ⋅ θ (T min (x,y)+15) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-3)) θ (1- θ (T min (x,y)+2)) ✓ Субполярный субгумидный:

K 5 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-0.5) ⋅ θ (T min (x,y)+15) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-3)) θ (1- θ (T min (x,y)+2)) θ (1- θ (MI(x,y)-1.0)).

Ель сибирская . Распространение ели сибирской в европейской части России и на Дальнем Востоке сдерживается геоботаническими и био-климатическими факторами. В европейской части России ель сибирская сменяется елью европейской при T_min выше -10 °С, а на Дальнем Востоке – елью аянской в районах, где средняя температура октября выше 0 ^оС.

Климатипы ели сибирской могут быть заданы в виде следующих рамочных моделей: в европейской части России –

• ✓    Суббореальный гумидный:

K 1 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅ θ (T min (x,y)+42) ⋅θ (P min (x,y)-40) θ (1- θ (T min (x,y)+10))

• ✓    Бореальный субгумидный:

K 2 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅ θ (T min (x,y)+42) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-6)) θ (1- θ (T min (x,y)+10)) θ (1- θ (MI(x,y)-1.0)) ✓ Бореальный гумидный:

K3={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅

⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+10))

• ✓    Субполярный гумидный:

K 4 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-3)) ⋅ ⋅θ (1- θ (T min (x,y)+10))

• ✓    Субполярный субгумидный:

K5={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-0.5) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-3)) ⋅ ⋅θ (1- θ (T min (x,y)+10)) θ (1- θ (MI(x,y)-1.0));

в Сибири –

• ✓    Суббореальный гумидный:

K 1 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-40) ⋅ ⋅θ (1- θ (T min (x,y)+2)) ⋅θ (T a (x,y)+5) ✓ Бореальный субгумидный:

K2={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-6)) ⋅ θ (1- θ (T min (x,y)+2)) θ (1- θ (MI(x,y)-1.0))) ⋅ ⋅θ (T a (x,y)+5) ✓ Бореальный гумидный:

K 3 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+2))) ⋅θ (T a (x,y)+5) ✓ Субполярный гумидный:

K4={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-25) θ (1- θ (BT(x,y)-3)) ⋅ ⋅θ (1- θ (T min (x,y)+2)) ⋅θ (T max (x,y)-12.5) ✓ Субполярный субгумидный:

K 5 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-0.25) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-25) ⋅ ⋅θ (1- θ (BT(x,y)-3)) θ (1- θ (T min (x,y)+2)) ⋅ ⋅θ (1- θ (MI(x,y)-1.0)) ⋅θ (T max (x,y)-12.5) ✓ Бореальный субгумидный мерзлотный: K 6 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.25) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-25) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+2)) θ (1- θ (MI(x,y)-1.0)) ⋅ ⋅θ (1- θ (T a (x,y)+5)) ⋅θ (T max (x,y)-12.5)

• ✓    Бореальный гумидный мерзлотный: K 7 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-25) θ (1-(BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+2)) θ (1- θ (T a (x,y)+5)) ⋅ ⋅θ (T max (x,y)-12.5);

на Дальнем Востоке:

• ✓    Суббореальный гумидный:

K1={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-40) ⋅ ⋅θ (1- θ (T min (x,y)+2)) ⋅θ (T a (x,y)+5) ⋅ ⋅θ (1- θ (T oct (x,y)))

• ✓    Бореальный субгумидный:

K 2 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-40) ⋅ ⋅θ (1- θ (BT(x,y)-6)) θ (1- θ (T min (x,y)+2)) ⋅ θ (1- θ (MI(x,y)-1.0))) ⋅θ (T a (x,y)+5) ⋅ ⋅θ (1- θ (T oct (x,y)))

• ✓    Бореальный гумидный:

K 3 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-40) ⋅ ⋅θ (1- θ (BT(x,y)-6)) ⋅θ (1- θ (T min (x,y)+2))) ⋅ ⋅θ (T a (x,y)+5) θ (1- θ (T oct (x,y)))

• ✓    Субполярный гумидный:

K 4 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-25) ⋅ ⋅θ (1- θ (BT(x,y)-3)) θ (1- θ (T min (x,y)+2)) ⋅ ⋅θ (T max (x,y)-12.5) θ (1- θ (T oct (x,y)))

• ✓    Субполярный субгумидный:

K 5 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-0.25) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-25) ⋅ ⋅θ (1- θ (BT(x,y)-3)) θ (1- θ (T min (x,y)+2)) ⋅ ⋅θ (1- θ (MI(x,y)-1.0)) ⋅θ (T max (x,y)-12.5) ⋅ ⋅θ (1- θ (T oct (x,y)))

• ✓    Бореальный субгумидный мерзлотный:

K 6 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.25) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-25) ⋅ ⋅θ (1- θ (BT(x,y)-6)) θ (1- θ (T min (x,y)+2)) ⋅θ (1- θ (MI(x,y)-1.0)) θ (1- θ (T a (x,y)+5)) ⋅ ⋅θ (T max (x,y)-12.5) θ (1- θ (T oct (x,y)))

• ✓    Бореальный гумидный мерзлотный:

K7={{x,y}: F(x,y)=1 }; F(x,y)=θ(BT(x,y)-3)⋅θ(MI(x,y)-1)⋅θ(Tmin (x,y)+42)⋅θ(Pmin (x,y)-25)θ(1-θ(BT(x,y)-6))θ(1-θ(Tmin (x,y)+2))θ(1-θ(Ta (x,y)+5))⋅θ(Tmax (x,y)-12.5)θ(1-θ(Toct (x,y))), где:

Ta – среднегодовая температура, °С;

Tmax – температура самого теплого летнего месяца, °С;

Toct – средняя температура октября. Критерий, на основании которого определяется граница распространения ели сибирской, связанная с геоботаническими факторами.

Предполагается, что ель аянская лучше адаптирована к условиям теплой осени, типичным для морского климата Приморья, чем ель сибирская, ареал которой в основном находится в районах с континентальным и резко континентальным климатом.

Ель аянская. Ель аянская распространена в Приморье, Корее, Японии, северо-востоке Китая, встречается в Южной Якутии. Климатические условия ее ареала характеризуются относительно теплой осенью и дождливым летом.

Климатипы ели аянской могут быть заданы в виде следующей рамочной модели:

• ✓    Суббореальный гумидный:

K 1 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-50) ⋅ ⋅θ (1- θ (T min (x,y)+2)) ⋅θ (T a (x,y)+5) ⋅ ⋅θ (T oct (x,y)+5))

• ✓    Бореальный субгумидный:

K 2 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.75) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+2)) θ (1- θ (MI(x,y)-1.0))) ⋅ ⋅θ (T a (x,y)+5) ⋅θ (T oct (x,y)+5))

• ✓    Бореальный гумидный:

K 3 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+2))) ⋅θ (T a (x,y)+5) ⋅ ⋅θ (T oct (x,y)+5))

• ✓    Субполярный гумидный:

K 4 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-50) ⋅ ⋅θ (1- θ (BT(x,y)-3)) θ (1- θ (T min (x,y)+2)) ⋅ ⋅θ (T max (x,y)-10) ⋅θ (T oct (x,y)+5)) ✓ Субполярный субгумидный:

K5={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-0.75) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-50) ⋅ ⋅θ (1- θ (BT(x,y)-3)) θ (1- θ (T min (x,y)+2)) ⋅ ⋅θ (1- θ (MI(x,y)-1.0)) ⋅θ (T max (x,y)-10) ⋅ ⋅θ (T oct (x,y)+5))

• ✓    Бореальный субгумидный мерзлотный:

K 6 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.75) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-25) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+2)) θ (1- θ (MI(x,y)-1.0)) ⋅ ⋅θ (1- θ (T a (x,y)+5)) ⋅θ (T max (x,y)-10) ⋅ ⋅θ (T_oct (x,y)+5))

• ✓    Бореальный гумидный мерзлотный:

K 7 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+2)) θ (1- θ (T a (x,y)+5)) ⋅ ⋅θ (T max (x,y)-10) ⋅θ (T oct (x,y)+5)).

Сосна обыкновенная. Сосна обыкновенная может произрастать в широком диапазоне климатических условий. Несмотря на высокую жароустойчивость и засухоустойчивость, происходит смена сосны обыкновенной другими породами в районах, где T_min выше -0,5 °С. В Сибири сосна распространяется не так далеко на север, как ель.

Климатипы сосны обыкновенной могут быть заданы в виде следующих рамочных моделей: в европейской части России –

• ✓    Суббореальный субгумидный:

K 1 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-0.75) ⋅ ⋅θ (1- θ (MI(x,y)-1.0)) ⋅θ (P min (x,y)-40) ⋅ ⋅θ (T min (x,y)+40)(1- θ (T min (x,y)+0.5)) ✓ Суббореальный гумидный:

K2={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) ⋅ ⋅θ (1- θ (T min (x,y)+0.5))

• ✓    Бореальный субгумидный:

K 3 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅

⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) θ (1- θ (MI(x,y)-1.0)) ⋅ ⋅θ (T a (x,y)+5)

• ✓    Бореальный гумидный:

K4={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅

⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) ⋅θ (T a (x,y)+5)

• ✓    Субполярный гумидный:

K 5 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-1) ⋅

⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-3)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5))

• ✓    Субполярный субгумидный:

K 6 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-0.5) ⋅

⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-3)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) θ (1- θ (MI(x,y)-1.0));

в Сибири –

• ✓    Суббореальный субгумидный:

K 1 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-0.75) ⋅ ⋅θ (1- θ (MI(x,y)-1.0)) ⋅θ (P min (x,y)-40) ⋅ ⋅θ (T min (x,y)+40)(1- θ (T min (x,y)+0.5))

• ✓    Суббореальный гумидный:

K 2 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) ⋅ ⋅θ (1- θ (T min (x,y)+0.5))

• ✓    Бореальный субгумидный:

K 3 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅

⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) θ (1- θ (MI(x,y)-1.0)) ✓ Бореальный гумидный:

K 4 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅

⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5))

• ✓    Субполярный гумидный:

K5={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-1) ⋅

⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-3)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) ⋅θ (T max (x,y)-15)

• ✓    Субполярный субгумидный:

K 6 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-0.5) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-3)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) θ (1- θ (MI(x,y)-1.0)) ⋅ ⋅θ (T max (x,y)-15)

• ✓    Бореальный субгумидный мерзлотный: K 7 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) θ (1- θ (MI(x,y)-1.0)) ⋅ ⋅θ (T max (x,y)-15) θ (1- θ (T a (x,y)+5))

• ✓    Бореальный гумидный мерзлотный: K 8 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) ⋅θ (T max (x,y)-15) ⋅ ⋅θ (1- θ (T a (x,y)+5))

на Дальнем Востоке –

• ✓    Суббореальный субгумидный: K 1 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-0.75) ⋅ ⋅θ (1- θ (MI(x,y)-1.0)) ⋅θ (P min (x,y)-40) ⋅ ⋅θ (T min (x,y)+40)(1- θ (T min (x,y)+0.5)) ⋅ ⋅θ (1- θ (T oct (x,y)+3))

• ✓    Суббореальный гумидный:

K 2 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) θ (1- θ (T oct (x,y)+3))

• ✓    Бореальный субгумидный:

K 3 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) θ (1- θ (MI(x,y)-1.0)) ⋅ ⋅θ (1- θ (T oct (x,y)+3))

• ✓    Бореальный гумидный:

K 4 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) θ (1- θ (T oct (x,y)+3))

• ✓    Субполярный гумидный:

K5={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-1) ⋅

⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-3)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) ⋅θ (T max (x,y)-15) ⋅

⋅θ (1- θ (T oct (x,y)+3))

• ✓    Субполярный субгумидный:

K 6 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-0.5) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-3)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) θ (1- θ (MI(x,y)-1.0)) ⋅ ⋅θ (T max (x,y)-15) θ (1- θ (T oct (x,y)+3))

• ✓    Бореальный субгумидный мерзлотный:

K 7 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) θ (1- θ (MI(x,y)-1.0)) ⋅ ⋅θ (T max (x,y)-15) θ (1- θ (T a (x,y)+5)) ⋅ ⋅θ (1- θ (T oct (x,y)+3))

• ✓    Бореальный гумидный мерзлотный: K 8 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-40) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) ⋅θ (T max (x,y)-15) ⋅ ⋅θ (1- θ (T a (x,y)+5)) θ (1- θ (T oct (x,y)+3)).

Сосна кедровая сибирская. Распространение сосны кедровой сибирской в европейской части России ограничивается районами, где T_min ниже -16 ^оС, а в Сибири, в зоне вечной мерзлоты, где T_max выше 15,5 ^оС. В Забайкалье при T_max ниже 16,5 ^оС и на Дальнем Востоке сосна кедровая сибирская сменяется кедровым стлаником.

Климатипы сосны кедровой сибирской могут быть заданы в виде следующих рамочных моделей:

в европейской части России –

• ✓    Суббореальный субгумидный:

K 1 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-0.75) ⋅ ⋅θ (1- θ (MI(x,y)-1.0)) ⋅θ (P min (x,y)-50) ⋅ ⋅θ (T min (x,y)+40)(1- θ (T min (x,y)+16))

• ✓    Суббореальный гумидный:

K 2 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-50) ⋅ ⋅θ (1- θ (T min (x,y)+16))

• ✓    Бореальный субгумидный:

K 3 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+16)) θ (1- θ (MI(x,y)-1.0)) ✓ Бореальный гумидный:

K 4 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-50) ⋅ ⋅θ (1- θ (BT(x,y)-6)) θ (1- θ (T min (x,y)+16));

в Сибири –

• ✓    Суббореальный субгумидный:

K 1 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-0.75) ⋅ ⋅θ (1- θ (MI(x,y)-1.0)) ⋅θ (P min (x,y)-50) ⋅ ⋅θ (T min (x,y)+40)(1- θ (T min (x,y)+16))

• ✓    Суббореальный гумидный:

K 2 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-50) ⋅ ⋅θ (1- θ (T min (x,y)+16))

• ✓    Бореальный субгумидный:

K₃={{x,y}: F(x,y)=1}; F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-6)) θ (1- θ (T min (x,y)+16)) θ (1- θ (MI(x,y)-1.0)) ⋅θ (T a (x,y)+5)

• ✓    Бореальный гумидный:

K 4 ={{x,y}: F(x,y)=1 };

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+16)) ⋅θ (T a (x,y)+5)

• ✓    Бореальный субгумидный мерзлотный:

K7={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) θ (1- θ (MI(x,y)-1.0)) ⋅

⋅θ (T max (x,y)-15.5) θ (1- θ (T a (x,y)+5))

• ✓    Бореальный гумидный мерзлотный:

K 8 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+40) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+0.5)) ⋅θ (T max (x,y)-15.5) ⋅ ⋅θ (1- θ (T a (x,y)+5)).

Лиственница Сукачева. Распространение лиственницы Сукачева в европейской части России ограничивается районами, где T_min ниже -13 °С. Ее климатипы могут быть заданы в виде следующей рамочной модели:

• ✓    Суббореальный субгумидный:

K 1 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) θ (1- θ (BT(x,y)-6.5)) ⋅ ⋅θ (MI(x,y)-0.5) θ (1- θ (MI(x,y)-1.0)) ⋅θ (P min (x,y)-50) ⋅

⋅θ (T min (x,y)+50)(1- θ (T min (x,y)+13))

• ✓    Суббореальный гумидный:

K2={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) θ (1- θ (BT(x,y)-6.5)) ⋅ ⋅θ (MI(x,y)-1.0) ⋅θ (T min (x,y)+50) ⋅

⋅θ (P min (x,y)-50) θ (1- θ (T min (x,y)+13))

• ✓    Бореальный субгумидный:

K 3 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅ ⋅θ (T min (x,y)+50) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+13)) θ (1- θ (MI(x,y)-1.0)) ✓ Бореальный гумидный:

K 4 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+50) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+13)).

Лиственница сибирская. Распространение лиственницы сибирской в Сибири ограничивается районами, где T_a ниже 0 ^оС, но выше -6 ^оС. В районах, где T_a ниже -6 ^оС, а также в Забайкалье она сменяется лиственницей даурской. Климати-пы лиственницы сибирской могут быть заданы в виде следующей рамочной модели:

• ✓    Суббореальный субгумидный:

K 1 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-0.5) ⋅ ⋅θ (1- θ (MI(x,y)-1.0)) ⋅θ (P min (x,y)-50) ⋅ ⋅θ (T min (x,y)+42)(1- θ (T min (x,y)+16)) ⋅ ⋅θ (T a (x,y)+5) θ (1- θ (T a (x,y)))

• ✓    Суббореальный гумидный:

K 2 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-6) ⋅θ (MI(x,y)-1.0) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-50) ⋅ ⋅θ (1- θ (T min (x,y)+16)) ⋅θ (T a (x,y)+5) θ (1- θ (T a (x,y)))

• ✓    Бореальный субгумидный:

K 3 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+16)) θ (1- θ (MI(x,y)-1.0)) ⋅ ⋅θ (T a (x,y)+5) θ (1- θ (T a (x,y)))

• ✓    Бореальный гумидный:

K 4 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅

⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+16)) ⋅θ (T a (x,y)+5) θ (1- θ (T a (x,y))) ✓ Субполярный гумидный:

K 5 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-1) ⋅

⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-3)) ⋅ ⋅θ (1- θ (T_min (x,y)+16)) ⋅θ (T_a (x,y)+6) θ (1- θ (T_a (x,y)))

• ✓    Субполярный субгумидный:

K 6 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-2.5) ⋅θ (MI(x,y)-0.5) ⋅

⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-3)) ⋅ ⋅θ (1- θ (T min (x,y)+16)) θ (1- θ (MI(x,y)-1.0)) ⋅ ⋅θ (T a (x,y)+6) θ (1- θ (T a (x,y)))

• ✓    Бореальный субгумидный мерзлотный:

K 7 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-0.5) ⋅

⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-6)) ⋅

⋅θ (1- θ (T min (x,y)+16)) θ (1- θ (MI(x,y)-1.0)) ⋅ ⋅θ (T a (x,y)+6) θ (1- θ (T a (x,y)+5))

• ✓    Бореальный гумидный мерзлотный:

K 8 ={{x,y}: F(x,y)=1};

F(x,y)= θ (BT(x,y)-3) ⋅θ (MI(x,y)-1) ⋅ ⋅θ (T min (x,y)+42) ⋅θ (P min (x,y)-50) θ (1- θ (BT(x,y)-6)) ⋅ ⋅θ (1- θ (T min (x,y)+16)) ⋅θ (T a (x,y)+6) ⋅ ⋅θ (1- θ (T a (x,y)+5)).

Обсуждение

Предлагаемые рамочные модели климатипов разделяют территорию России на климатопы (рисунок) – районы, которые можно считать относительно однородными по биоклиматическим факторам среды. Так как абсолютно идентичных условий произрастания практически не бывает, то

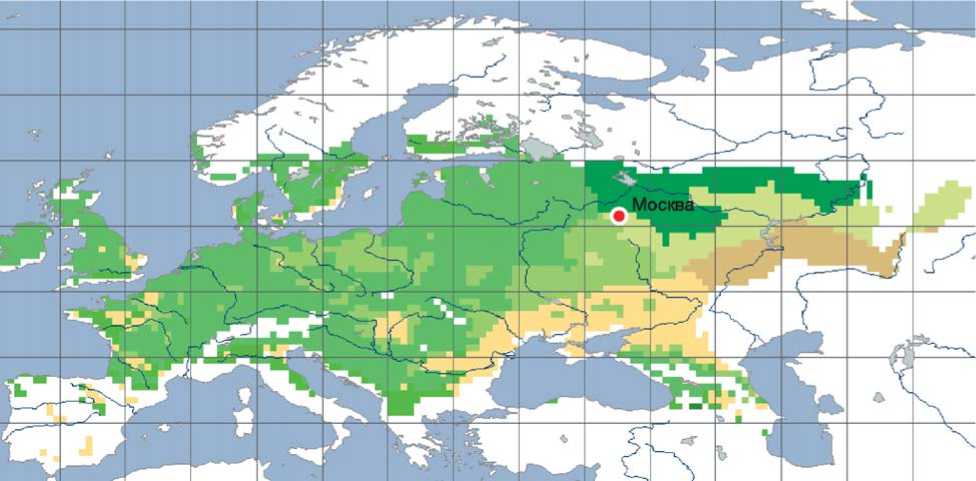
Не входит в ареал

Субгумидный засухоустойчивый

Субгумидный морозостойкий засухоустойчивый

Субгумидный морозостойкий

Субгумидный

Гумидный морозостойкий

Гумидный засухоустойчивый

Гумидный

Гумидный морозостойкий засухоустойчивый

Климатопы дуба черешчатого

выделенные климатопы можно фрагментировать по задаваемым параметрам, моделируя различные варианты климатических условий. Однако не все различия в климатических условиях местопроизрастания являются существенными для инициации механизмов генетической адаптации. Вариации климатических условий, которые укладываются в рамки фенотипической пластичности древесной породы, необязательно приводят к формированию климатипов, т.е. адаптация к условиям произрастания может выражаться в фенотипических признаках, которые проявляются в течение жизни одного поколения и не передаются по наследству. Существенными можно считать межбиомные различия климатических условий [13]. Есть основания полагать, что популяции древесных пород, произрастающие в разных биомах, отличаются генетически. Чтобы проверить эту почти очевидную гипотезу, необходимо провести широкомасштабные эколого-генетические исследования. Пример таких исследований – широкомасштабное изучение генетического разнообразия дуба черешчатого (а именно, вариаций ДНК хлоропластов), проведенное с 1996 по 2000 г. [14]. В процессе исследования обследовано более 2,5 тыс. популяций, более 12,5 тыс. деревьев и выявлено 39 гаплотипов, 7 из которых встречаются на территории Российской Федера- ции. Собранный материал предоставляет определенные возможности для разработки генетикоэкологического подхода к выделению климати-пов дуба черешчатого, но преждевременно предполагать, что он дает исчерпывающий ответ на вопрос о том, как выделять соответствующие им климатопы. Поэтому традиционное использование термина «климатип» для обозначения популяций древесной породы, произрастающих в существенно различающихся климатических условиях, – по-прежнему актуально.

Заключение

Рамочные модели климатипов необходимы для уточнения неблагоприятных воздействий, которые может оказать на лесное хозяйство предполагаемое изменение глобального климата. Метапопуляционный анализ [15] служит одним из инструментов для оценки реакции редких видов животных или растений на изменения окружающей среды [16]. Он также может быть использован для разработки системной стратегии адаптации лесного хозяйства к предполагаемым изменениям климата [17]. Рамочные модели климатипов основных древесных пород – первый шаг в этом направлении.