Биомеханическое моделирование артерий головного мозга при разных вариантах конструкции внутричерепных артерий вертебробазилярной системы

В современном мире анализ анатомических и экспериментальных данных трудно представить без использования компьютерных программ, требующих введения многочисленных количественных показателей и применения математического аппарата анализа данных [1]. Метод моделирования — один из главных инструментов изучения различных объектов, явлений и процессов. Разрабатываемые модели позволяют при необходимости воспроизводить наглядные трехмерные конструкции изучаемых объектов и наблюдать за их изменениями в процессе корректировки отдельных параметров в соответствии с поставленными задачами.

При построении компьютерной модели артерий мозга необходимо учитывать их морфологию, гемодинамические параметры течения крови и механические свойства артериальной стенки [2–4]. Сведения об основных морфологических данных и гемодинамических параметрах человека можно получить по результатам современных методов инструментальной диагностики. Прижизненное определение механических параметров сосудов человека в настоящее время не представляется возможным. В связи с этим изучение биомеханических свойств мозговых сосудов на трупном материале имеет существенное значение.

Моделирование кровотока человека по мозговым артериям может быть полезно для оптимизации реконструктивных операций на этих артериях и позволило бы прогнозировать некоторую патологию, например развитие аневризмы. Следовательно, компьютерные модели должны быть максимально приближены к реальным объектам, а в идеале должны строиться индивидуальные (пациентоориентированные) модели артерий головного мозга, с помощью которых можно достаточно точно выявить и оценить индивидуальные особенности анатомического строения и ряд функциональных параметров мозговых артерий. Индивидуальная компьютерная модель позволит грамотно провести предоперационную подготовку пациента, оценить степень эффективности соответствующих хирургических вмешательств, дать рекомендации оперирующему хирургу.

Моделирование мозговых артерий неоднократно предпринималось, в основном зарубежными специалистами. Построены и проанализированы модели классического артериального круга головного мозга, а также модели с его вариантами и аномалиями (отсутствие одной из составляющих круг артерий, стеноз артерий, наличие аневризмы и т.д.) [4–7]. Во всех указанных моделях предполагалось, что стенка артерий была жесткой, т.е. не учитывали влияние на мозговой кровоток биомеханических параметров артериальной стенки.

Занимаясь вопросами морфологии и биомеханики артерий головного мозга [8, 9], мы обратили внимание на наличие корреляционной зависимости ряда морфологических и биомеханических параметров от углов соединения позвоночных и бифуркации базилярной артерий.

Цель: биомеханическое моделирование артерий головного мозга при разных вариантах конфигурации внутричерепных артерий вертебробазилярной системы.

Материал и методы. Моделирование артерий головного мозга человека осуществлено на основании изученных нами морфометрических (длина, толщина стенки, наружный диаметр, диаметр просвета) и биомеханических (общая прочность, предел прочности, максимальная относительная деформация, модуль Юнга) параметров передних, средних и задних мозговых, задних соединительных, базилярной и внутричерепных частей позвоночных артерий, полученных при аутопсии 110 взрослых людей [8, 9]. Биомеханические модели артерий головного мозга построены в системе конечно-элементного анализа ANSYS. Алгоритм решения задачи методом конечных элементов состоял из следующих этапов:

• 1.    Выбор математической модели, т.е. выбор дифференциальных уравнений, описывающих исследуемый процесс, в нашем случае выбор модели течения крови и модели движения артериальной стенки.

• 2.    Импорт геометрической модели артерий головного мозга.

• 3.    Задание свойств материала и граничных условий.

• 4.    Генерация сетки конечных элементов.

• 5.    Решение задачи (построение биомеханической модели) с последующей визуализацией и обработкой полученных данных.

Выбор математической модели. Течение крови описывается системой уравнений Навье–Стокса, а движения артериальной стенки — уравнениями Навье–Ламе.

Замкнутая система уравнений Навье — Стокса (три уравнения движения и уравнение неразрывности) выглядит следующим образом:

8 V;    5 v, p —^ + ^v ( 81   8xj *

j

= fi-Il p + P ^{V 2} V i , 8 x.

divv = 0, 8 ²

V ²

где

8 x² - оператор Лапласа в декартовой системе координат; ∂ — знак частной производной;

ν _i — компоненты вектора скорости крови; x _j — пространственные координаты; p — давление крови; µ — коэффициент динамической вязкости крови; индексы i , j пробегают значения от 1 до 3.

Векторная форма уравнения движения крови выглядит следующим образом:

• 8 v            f 1     , и

  --+ ( v • V ) v =  --- gradp +— A v ,     divv = 0, 8 t          P P P

v=—■ e где    8xi 1 — оператор Гамильтона в декартовой системе координат; gradp — градиент давления.

Уравнения Навье–Ламе выводятся из уравнений движения сплошной среды при подстановке в них выражений для компонентов тензора напряжений и компонентов тензора малых деформаций p j = X I 1 ( е ) S j + 2це^ , а также соотношений Коши, связывающих компоненты тензора малых деформаций и компоненты вектора перемещения

^E i

• 1    8u

L + — ,

• 2    8x-8x.

• V j        1

где X , и — упругие константы Ламе, характеризующие механические свойства материала среды; I 1 ( е ) — первый инвариант тензора малых деформаций.

Уравнения Ламе имеют вид

(X + и)grad div u + pAu + pF = pa,

где a — ускорение.

В декартовой системе координат их можно записать следующим образом:

P a x

8 ( 8 u

8 w

+   +     1 + и

8 x   8 y   8 z j

p a y

d ( d u

d w

p a z

— I — + — + — 1 + P 8y (dx dy dz ) I д (du 8 v 8 w 7 ( 1111 + pl

8 z (8 x 8 y 8 z j

82 u 82 u 82 u 7„

+    +      1 + p F , ,

8x   8y

' 82 v  82 v 82 v )

++ 1 + p F, 8 x ² 8 y ² 8 z ² j y

8 ² w 8 ² w 8 ² w 7

—г + —r + —г 1 + pFz, 8x   8y    8z j где через и, v, w обозначены компоненты вектора перемещений и, а Fx, Fy. Fz — компоненты внешних объемных сил, которые в данной работе не учитывались.

Система уравнений Ламе для динамических задач становится замкнутой, если к ней добавить опре

• - dv д v     д v - du

• a = — =--+ v, —, v = —.

деление ускорения d    д t     д x i d

Импорт геометрической модели. Геометрическая модель артерий головного мозга восстановлена посредством обработки результатов магнитно-резонансной томографии, полученных из архива кафедры лучевой диагностики и лучевой терапии им. профессора Н. Е. Штерна Саратовского медицинского университета. Обработка данных магнитно-резонансной томографии и последующего их преобразования в 3D-модели произведена в полуавтоматическом режиме с использованием специализированного программного обеспечения Mimics. В программный пакет данного приложения загружали снимки головы женщины 2-го периода зрелого возраста, после чего выбран диапазон оттенков серого, соответствующий плотности крови, а на основе этих данных автоматически воспроизведена геометрическая модель (рис. 1). В полученном изображении с помощью программных средств Mimics удалены все элементы сосудистого русла, которые не планируется использовать в дальнейших расчетах, а также элементы, плотность которых близка к плотности крови, что позволило им ошибочно попасть в интересующий нас диапазон.

Полученная таким образом геометрическая модель сохранена в формате STL, что позволило в дальнейшем импортировать ее в CAD-систему для сглаживания геометрии, т.е. построения модели без неровностей и искажений. Дальнейшее построение трехмерной модели проводилось в программном пакете SolidWorks. При восстановлении геометрии предполагалось, что все сосуды имеют круговое поперечное сечение. С помощью инструмента «вытягивание по сечениям» построена твердотельная модель артерий головного мозга (рис. 2).

Следует отметить, что стенки сосудов в импортированной из Mimics геометрии отсутствовали, так как их плотность выше, чем у крови, и, следовательно, на томограмме стенкам артерий соответствовал другой диапазон серого цвета. В связи с этим стенки артерий достроены в пакете SolidWorks в соответствии с морфометрическими данными, характерными для женщины 2-го периода зрелого возраста [8].

Задание свойств материала и граничных условий. Биомеханические параметры артерий, используемые для построения стенок модели артерий, взяты в соответствии с возрастно-половой принадлежностью субъекта из наших предыдущих работ, т.е. взяты соответствующие параметры артерий женщины 2-го периода зрелого возраста [9]. Стенки артерий считались идеально упругими, изотропными и несжимаемыми. Для задания механических свойств рассчитывали модуль Юнга, а коэффициент Пуассона для несжимаемого материала считали равным 0,49.

Кровь рассматривалась вязкой, несжимаемой, однородной ньютоновской жидкостью с постоянной вязкостью, равной 0,004 Па*с и плотностью p = 1050 г/м³. На входе в позвоночные и внутренние сонные артерии задавали скорости потока крови, полученные по результатам ультразвукового исследо-

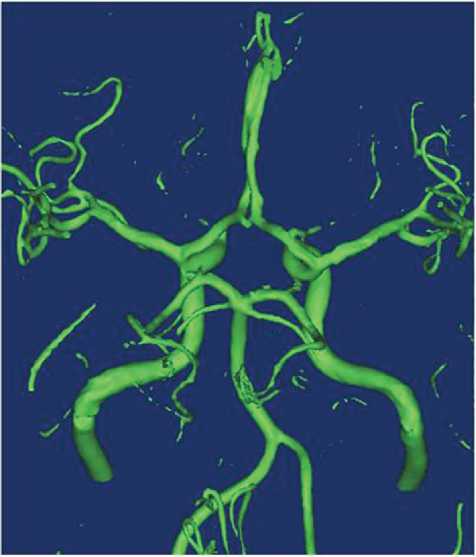
Рис. 1. Геометрическая модель артерий головного мозга, построенная в программе Mimics

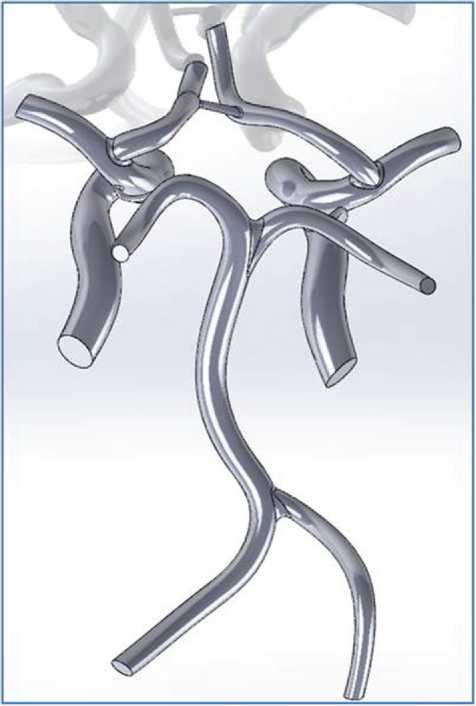
Рис. 2. Твердотельная модель артерий головного мозга

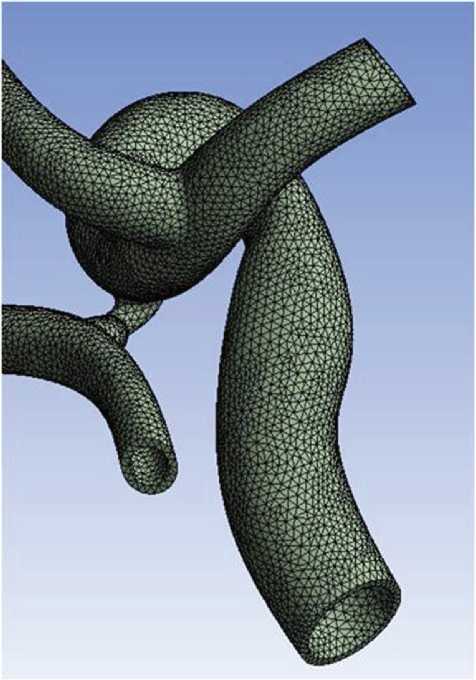
Рис. 3. Фрагмент вычислительной сетки сглаженной трехмерной модели артерий головного мозга вания сосудов той же женщины 2-го периода зрелого возраста.

Генерация сетки конечных элементов. В работе строилась трехмерная тетраэдрическая вычислительная сетка (рис. 3).

Биомеханические модели в данной работе построены для артерий головного мозга взрослых людей при разных вариантах конфигурации внутричерепного отдела вертебробазилярной системы. Для этого в построенной модели для человека 2-го периода зрелого возраста (с определенными морфометрическими и биомеханическими параметрами сосу- дистой стенки, одинаковыми свойствами материала стенки, одинаковыми граничными условиями) были изменены величины угла соединения (УС) внутричерепных частей позвоночных артерий (ВЧПА) и угла бифуркации (УБ) базилярной артерии (БА) (табл. 1).

В построенных моделях сравнивали параметры движения крови (объемная скорость кровотока) и напряженно-деформированного состояния артериальных стенок (эффективные напряжения по Мизесу). Объемная скорость кровотока — это объем крови, протекающий через поперечное сечение сосуда в единицу времени. Измеряется в м3/с. Эффективные (эквивалентные) напряжения (по Мизесу) — критерий, использующийся при расчете различных конструкций (в нашем случае артериальной стенки) на их прочность, т.е. способность выдерживать внешние нагрузки, не разрушаясь. Чем выше значение эффективных напряжений, тем сильнее напрягается материал, и места, в которых эффективные напряжения максимальны, наиболее подвержены разрушению. Измеряется в паскалях (Па). Также в работе использовали такие понятия, как давление крови и касательные напряжения. Давление крови — это давление, которое кровь оказывает на стенки кровеносных сосудов, или, иначе говоря, превышение давления жидкости в кровеносной системе над атмосферным. Измеряется в паскалях (Па). Касательные напряжения на стенке сосуда — это сдвиговые напряжения, возникающие между сосудистой стенкой и слоем жидкости (кровью) рядом со стенкой. Возникают из-за наличия вязкости крови вследствие ее трения о стенку сосуда. Измеряются в паскалях (Па).

Все параметры оценивались в течение второго рассчитываемого сердечного цикла. Это связано с тем, что течение крови во вторую секунду начинается не с нулевой скорости и давления, а исходя из рассчитанной первой секунды. Таким образом, во вторую секунду расчетов мы получаем более реалистичное поведение сосудов и более точные числовые значения характеристик потока и движения стенок.

Полученные данные обрабатывали вариационностатистическим методом с использованием пакета прикладных программ Statistica-6 и Microsoft Exсel Windows-XP. Изучаемые параметры находились в диапазоне нормального распределения. В связи с этим определяли минимальное и максимальное значения, среднюю арифметическую (М), ошибку средней арифметической (m), среднее квадратическое

Варианты конфигурации внутричерепного отдела вертебробазилярной системы

Таблица 1

№	Вариант конфигурации	Интервал значений углов, характерный для данного варианта конфигурации, град.		Величины углов, использованные при моделировании, град.
		УС ВЧПА	УБ БА	УС ВЧПА	УБ БА
1	Узкий УС ВЧПА и средний УБ БА	29,10–42,0	87,29–130,11	30	110
2	Узкий УС ВЧПА и широкий УБ БА	29,10–42,0	130,12–169,40	30	160
3	Средний УС ВЧПА и средний УБ БА	42,10–70,56	87,29–130,11	60	110
4	Средний УС ВЧПА и широкий УБ БА	42,10–70,56	130,12–169,40	60	160
5	Широкий УС ВЧПА и средний УБ БА	70,57–92,0	87,29–130,11	90	110
6	Широкий УС ВЧПА и широкий УБ БА	70,57–92,0	130,12–169,40	90	160
7	Узкий УС ВЧПА и узкий УБ БА	29,10–42,0	59,40–87,28	30	60
8	Средний УС ВЧПА и узкий УБ БА	42,10–70,56	59,40–87,28	60	60
9	Широкий УС ВЧПА и узкий УБ БА	70,57–92,0	59,40–87,28	90	60

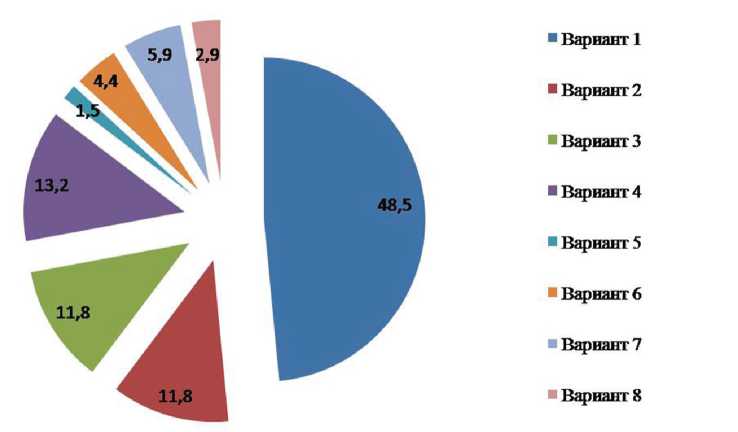
Рис. 4. Частота встречаемости вариантов конфигурации внутричерепных артерий вертебробазилярной системы

отклонение (σ), коэффициент вариации (Cv). Количество наблюдений в табл. 2 обозначено как n. Для оценки достоверности различий между рядами вариант использовали параметрический (критерий Стьюдента) статистический критерий достоверности. При этом различия считали достоверными при 95%-м пороге вероятности (р<0,05).

Результаты. Разные варианты конфигурации внутричерепных артерий вертебробазилярной системы встречаются с различной частотой (рис. 4). Наиболее часто встречается вариант №3, характеризующийся средней величиной УС ВЧПА и УБ БА. К редким типам (частота встречаемости 1,5%) отнесен вариант №7, при котором наблюдались узкие УС ВЧПА и УБ БА. На материале выполненного исследования, при наличии широкого УС ВЧПА, УБ БА никогда не был узким, т.е. вариант №9 выделен нами только теоретически.

На построенных моделях для всех вариантов конфигурации артерий вертебробазилярной системы выявлены следующие общие закономерности гемодинамических параметров и параметров напряженно-деформированного состояния сосудистой стенки:

• 1.    Похожая картина линий тока и скорости крови, когда наибольшее ускорение потока происходит в месте отхождения средних мозговых артерий. Наименьшие скорости течения обнаружены в соединительных артериях, а также в месте бифуркации БА и в месте соединения ВЧПА (рис. 5).

• 2.    Областям с наименьшими скоростями крови соответствуют области с наименьшими касательными напряжениями (рис. 6).

• 3.    Давление крови принимает наибольшее значение в апексе бифуркации БА и местах отхождения передних мозговых артерий (рис. 7).

• 4.    Наибольшие эффективные напряжения (напряжения по Мизесу) обнаруживаются в областях соединения ВЧПА и бифуркации БА (рис. 8).

5.440е-001 3.627е-001 0.000е+000

Объемный кровоток. Вариант конфигурации внутричерепных артерий вертебробазилярной системы

Velocity Streamline 1

Ш 7.253е-001

1.81 Зе-001

[m sA-1]

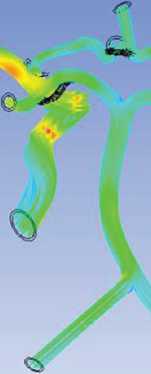
Рис. 5. Линии тока и скорость крови в артериях головного мозга, м/с

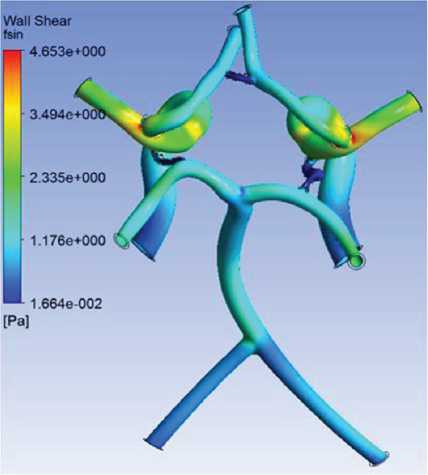
Рис. 6. Касательные напряжения на стенках артерий головного мозга, Па

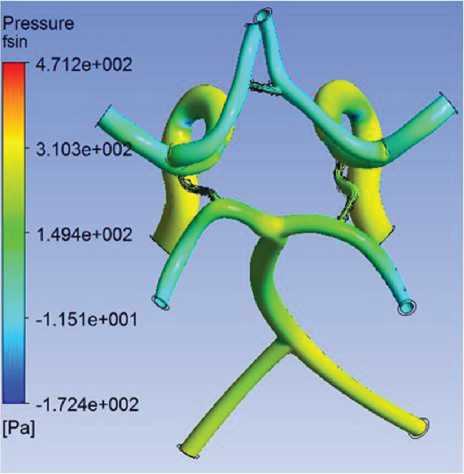
Рис. 7. Поля давления крови в артериях головного мозга, Па

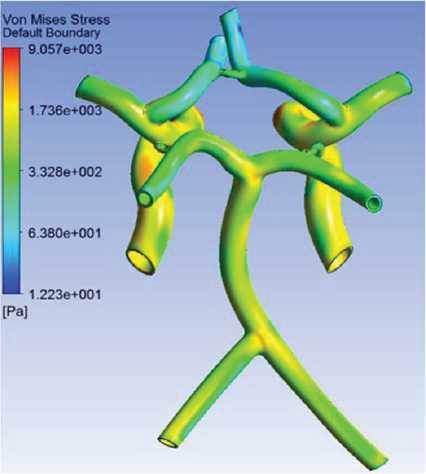
Рис. 8. Наибольшие эффективные напряжения (напряжения по Мизесу) в артериях головного мозга, Па

оказывает влияние на объемный кровоток в задних мозговых артериях (ЗМА) (рис. 9, 10).

Величины объемного кровотока в правой и левой ЗМА представлены в табл. 2. Наибольшие абсолютные значения в правой и в левой ЗМА данный параметр имеет при вариантах конфигурации №8 и 9; самые малые значения имеются у вариантов №3 и 5 для правой и в вариантах №4 и 6 для левой ЗМА. Левая ЗМА более вариабельная по изучаемому параметру, чем правая. Сравнительный анализ объ- емного кровотока в правой и левой ЗМА при разных вариантах конфигурации внутричерепных артерий вертебробазилярной системы показал наличие статистически значимых билатеральных различий. При условии одинакового среднего УБ БА объемный кровоток в левой ЗМА статистически значимо больше, чем в правой ЗМА: при узком УС ВЧПА (вариант №1) — на 24%, при среднем УС ВЧПА — на 3l % (вариант №3), при широком УС ВЧПА (вариант №5) — на 25% (р=0,004-0,019).

Таблица 2

№	Вариант конфигурации	Сторона	n	Вариационно-статистические показатели
				Min-max	М±m	σ	Cv
1	Узкий УС ВЧПА и средний УБ БА	П Л	11 11	0,67–1,18 0,82–1,48	0,88±0,05 1,09±0,07	0,17 0,22	19,4 20,0
2	Узкий УС ВЧПА и широкий УБ БА	П Л	11 11	0,70–1,22 0,75–1,43	0,92±0,05 1,04±0,07	0,17 0,22	18,4 21,1
3	Средний УС ВЧПА и средний УБ БА	П Л	11 11	0,64–1,12 0,83–1,48	0,83±0,05 1,09±0,06	0,16 0,21	19,1 19,8
4	Средний УС ВЧПА и широкий УБ БА	П Л	11 11	0,71–1,24 0,72–1,30	0,92±0,05 0,95±0,06	0,18 0,19	19,1 20,3
5	Широкий УС ВЧПА и средний УБ БА	П Л	11 11	0,66–1,18 0,83–1,48	0,87±0,05 1,09±0,07	0,17 0,22	19,8 19,9
6	Широкий УС ВЧПА и широкий УБ БА	П Л	11 11	0,71–1,26 0,77–1,40	0,93±0,06 1,03±0,06	0,18 0,21	19,7 20,4
7	Узкий УС ВЧПА и узкий УБ БА	П Л	11 11	0,75–1,30 0,76–1,50	0,98±0,05 1,09±0,07	0,18 0,23	17,8 21,4
8	Средний УС ВЧПА и узкий УБ БА	П Л	11 11	0,76–1,32 0,80–1,53	1,00±0,05 1,12±0,07	0,18 0,23	17,7 21,0
9	Широкий УС ВЧПА и узкий УБ БА	П Л	11 11	0,75–1,32 0,78–1,52	0,99±0,05 1,11±0,07	0,18 0,24	18,0 21,2

Объемная скорость кровотока в правой и левой ЗМА, см3/с

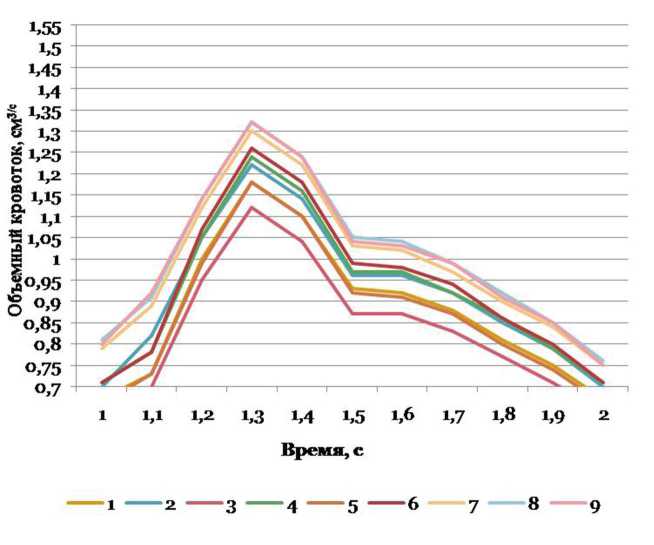
Рис. 9. Объемный кровоток в правой ЗМА при разных вариантах конфигурации внутричерепных артерий вертебробазилярной системы, см3/с

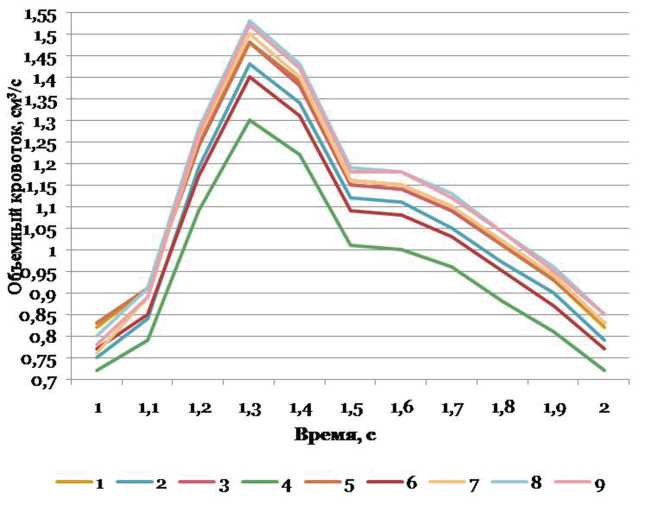
Рис. 10. Объемный кровоток в левой ЗМА при разных вариантах конфигурации внутричерепных артерий вертебробазилярной системы, см3/с

Обнаружены статистически значимые различия величины объемного кровотока в правой ЗМА при разных вариантах конфигурации внутричерепных артерий вертебробазилярной системы. При наиболее часто встречающемся варианте №3 (средние УС ВЧПА и УБ БА), объемный кровоток в правой ЗМА на 18% меньше, чем при варианте №7 (узкие УС ВЧПА и УБ БА), и на 20% меньше, чем в вариантах №8 и 9 (средний или широкий УС ВЧПА при узком УБ БА) (р=0,030–0,044).

Наибольшие эффективные напряжения (напряжения по Мизесу). Величины УС ВЧПА и УБ БА ока- зывают влияние на распределение эффективных напряжений в области бифуркации БА (рис. 11, табл. 3).

Наибольшие средние значения данный параметр имеет при вариантах конфигурации внутричерепных артерий вертебробазилярной системы №7, 8 и 9; самые малые значения — при вариантах №2 и 6.

Эффективные напряжения более вариабельны по сравнению с величиной скорости объемного кровотока (Cv колеблется в диапазоне 35,7-39,6%). Обнаружены статистически значимые различия эффективных напряжений при разных вариантах конфигурации внутричерепных артерий вертебробазилярной системы (табл. 4).

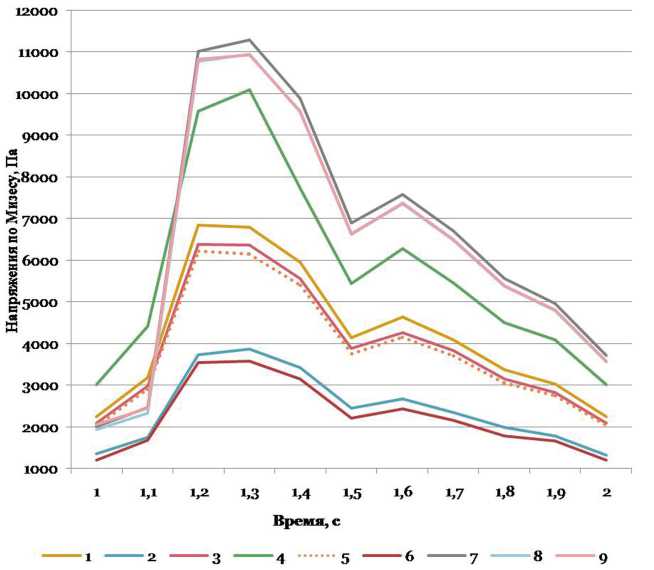
Рис. 11. Максимальные эффективные напряжения по Мизесу в области бифуркации БА при разных вариантах конфигурации внутричерепных артерий вертебробазилярной системы, Па

Таблица 3

Максимальные эффективные напряжения по Мизесу в области бифуркации БА, Па

№	Вариант конфигурации	n	Вариационно-статистические показатели
			Min-max	М±m	σ	Cv
1	Узкий УС ВЧПА и средний УБ БА	11	2245,54–7509,39	4319,45±348,15	1595,46	36,9
2	Узкий УС ВЧПА и широкий УБ БА	11	1330,10–4213,07	2460,55±192,12	880,43	35,7
3	Средний УС ВЧПА и средний УБ БА	11	2097,01–7009,92	4027,08±325,45	1491,42	37,0
4	Средний УС ВЧПА и широкий УБ БА	11	3006,48–10089,96	5822,96±479,06	2195,37	37,7
5	Широкий УС ВЧПА и средний УБ БА	11	2035,17–6810,12	3901,47±312,14	1430,44	36,6
6	Широкий УС ВЧПА и широкий УБ БА	11	1201,23–3914,29	2297,79±179,92	824,52	35,8
7	Узкий УС ВЧПА и узкий УБ БА	11	2000,00–12284,37	6723,85±661,64	3032,03	39,6
8	Средний УС ВЧПА и узкий УБ БА	11	1940,00–11967,72	6504,46±645,45	2957,83	38,9
9	Широкий УС ВЧПА и узкий УБ БА	11	2050,00–11956,84	6531,47±640,38	2934,63	39,4

Таблица 4

Различия величин эффективного напряжения в области бифуркации БА в зависимости от варианта конфигурации внутричерепных артерий вертебробазилярной системы, %

Вариант конфигурации	1	2	3	4	5	6	7	8	9
1	-	<0,001)	0,597	0,033	0,442	<0,001	0,006	0,010	0,009
2		-	<0,001	<0,001	0,001	0,596	<0,001	<0,001	<0,001
3			-	0,010	0,810	<0,001	0,002	0,003	0,003
4				-	0,006	<0,001	0,331	0,453	0,434
5					-	<0,001	0,001	0,002	0,001
6						-	<0,001	<0,001	<0,001
7							-	0,831	0,851
8								-	0,978

П р и м еч а н и е : полужирным шрифтом выделены статистически значимые различия.

При наиболее часто встречающейся конфигурации (средние УС ВЧПА и УБ БА) эффективные напряжения наиболее близки к варианту №1 (узкий УС ВЧПА и средний УБ БА) и №5 (широкий УС ВЧПА и средний УБ БА), различия с другими вариантами конфигураций варьируются от 44,6 до 75,3%.

Обсуждение. Математическое и компьютерное моделирование различных процессов, органов и систем организма человека прочно вошло в современную медицину. Симбиоз математики, биомеханики и клинических специальностей разного профиля нацелен на решение сложных задач, связанных с разработкой различных способов хирургического вмешательств дооперационно, «в отрыве» от пациента, что поможет снизить риск возможных осложнений. Компьютерное моделирование может быть полезно при прогнозировании возникновения той или иной патологии. Применительно к артериям головного мозга это может быть риск развития внутричерепных аневризм и ее разрыва, прогнозирование прогрессирования атеросклеротических отложений. При этом важно, чтобы модели наиболее полно отражали процессы в организме человека, т.е. были приближены к реальным. В большинстве работ по моделированию артерий головного мозга стенка артерий описана как жесткая, т.е. не учитывалось ее влияние на параметры кровотока [5–7]. Мы считаем, и в литературе имеется тому подтверждение [4], что морфология и биомеханические свойства сосуда оказывают значительное влияние на кровоток и модели с идеально упругими стенками более реально описывают гемодинамику и напряженно-деформированное состояние артериальной стенки.

Анализируя представленные модели артериальных сосудов, можно увидеть, что в зоне бифуркации БА давление потока крови достигает максимальных значений, в этих же зонах создаются концентрации максимальных эквивалентных напряжений. Действие этих гемодинамических факторов, особенно при их нарастании при динамическом наблюдении, способно привести к локальному ослаблению сосудистой стенки (в основном за счет разрушения средней оболочки артерий), что может содействовать образованию в этих областях аневризм [11]. Как известно, именно изгибы и бифуркации наиболее часто подвержены возникновению этой патологии. В исследованиях E.A. Sheffield и R. O. Weller [12] описаны возрастные изменения в стенках мозговых артерий, заключающиеся в образованиях дефектов их средней оболочки, локализующихся у 60% пациентов всех возрастов на боковых стенках бифуркации.

На полученных моделях в областях бифуркации БА, а также в месте соединения ВЧПА мы обнаружили некоторое замедление скорости кровотока и уменьшение касательных напряжений. Влияние низких касательных напряжений на развитие атеросклероза описано в работе A. M. Malek, S. L. Alper, S. Izumo (1999) [13]. Авторы заметили, что в случае низких касательных напряжений на стенке артерии уменьшается выработка простациклина и оксида азота, оба из которых препятствуют активации тромбоцитов, ослабляют пролиферацию гладких мышц и тормозят образование неоинтимы. Поэтому происходит адгезия моноцитов в эндотелий, что способствует образованию атеросклеротических отложений.

Заключение. Сочетанная изменчивость углов соединения позвоночных артерий и бифуркации базилярной артерии определяет 9 вариантов конфигурации внутричерепных артерий вертебробазилярной системы, которые встречаются с разной частотой. Вариант, характеризующийся средней величиной указанных углов, встречается чаще всего — в 49% случаев. Реже других (1,5% случаев) наблюдается вариант с узкими углами соединения позвоночных и бифуркации базилярной артерий. На материале нашего исследования, при наличии широкого угла соединения позвоночных артерий, угол бифуркации базилярной артерии на две задние мозговые артерии никогда не был узким.

При биомеханическом моделировании артерий головного мозга показано, что конфигурация внутричерепных артерий вертебробазилярной системы оказывает влияние на распределение кровотока в задних мозговых артериях и эффективных напряжений в области бифуркации базилярной артерии. Построенная индивидуальная биомеханическая модель позволяет судить о некоторых параметрах гемодинамики и напряженно-диформированного состояния сосудистой стенки, которые могут оказывать влияние на развитие атеросклероза и внутричерепных аневризм.