Biometric system design for iris recognition using intelligent algorithms
Автор: Muthana H. Hamd, Samah K. Ahmed
Журнал: International Journal of Modern Education and Computer Science @ijmecs
Статья в выпуске: 3 vol.10, 2018 года.
Бесплатный доступ
An iris recognition system for identifying human identity using two feature extraction methods is proposed and implemented. The first approach is the Fourier descriptors, which is based on transforming the uniqueness iris texture to the frequency domain. The new frequency domain features could be represented in iris-signature graph. The low spectrums define the general description of iris pattern while the fine detail of iris is represented as high spectrum coefficients. The principle component analysis is used here to reduce the feature dimensionality as a second feature extraction and comparative method. The biometric system performance is evaluated by comparing the recognition results for fifty persons using the two methods. Three classifiers have been considered to evaluate the system performance for each approach separately. The classification results for Fourier descriptors on three classifiers satisfied 86% 94%, and 96%, versus 80%, 92%, and 94% for principle component analysis when Cosine, Euclidean, and Manhattan classifiers were applied respectively. These results approve that Fourier descriptors method as feature extractor has better accuracy rate than principle component analysis.
Iris recognition, Fourier descriptors, Principle component analysis, feature extraction
Короткий адрес: https://sciup.org/15016742
IDR: 15016742 | DOI: 10.5815/ijmecs.2018.03.02
Текст научной статьи Biometric system design for iris recognition using intelligent algorithms
Published Online March 2018 in MECS DOI: 10.5815/ijmecs.2018.03.02
The traditional security techniques such as, passwords, codes, and ID cards are not confident in many applications so the demands for biometric systems has been increased to support and enhance the traditional security systems. Humans have many traits that can be used in a biometric system to identify their identity and hence to give them an authorization to access for example their bank accounts or even to pass the smart gate in airports. Traits could be face, fingerprints, voice, or iris. Biometric system based iris has many advantages over the others recognition system like face, voice, or fingerprint. Iris is stable through all human life, it does not affect by genetic gene or feeling of person. Also, it contains enrichment features that would be extracted later to generate the patterns. The biometric system based iris recognition is reliable and modern technique for preventing frauds and fakes operations [1]. This paper proposes new methods for building biometric system based iris recognition; it uses two comparative procedures to extract the iris feature and generate the input machine vectors. These methods are the Fourier descriptors (FDs) and Principle Component Analysis (PCA). FD describes the object contour by a set of numbers which represents the frequency content for full form, so any twodimensional object could be encoded by transforming its boundary into frequency domain complex numbers. The challenge is no previous research uses the shape descriptor procedure as a feature extractor in the frequency domain. The PCA is a static technique that widely used in image compression and face recognition applications for decreasing the data dimensionality. The paper could be organized as follows: section I is the introduction, section II and III explain the FD and PCA procedures and the proposed iris recognition system respectively. Section IV tabulates the recognition results of three distance measure methods; it shows the accuracy rate for each method that was applied on 50 iris images. Eventually, section V discusses and concludes the highest accuracy result and its related three distance measures.
-
II. Review of Related Work
In 1936 the ophthalmologist Burch suggested the idea of utilizing the iris in human identification. Aran and Flom in 1987 adopted Burch’s idea of identifying people based on their individual iris feature. In 2004, J. Daugman applied Gabor filters to create the iris phase code, he registered excellent accuracy rate on different number of iris datasets. He used Hamming distance between two bits for phase matching [1]. In 2004, Son et al., used linear discriminant analysis (LDA), Direct Linear Discriminate Analysis (DLDA), a Discrete Wavelet Transform (DWT), and PCA and to extract iris features [2]. In 2007, R. Al-Zubi and D. Abu-Al-Nadin applied a circular Hough transform and Sobel edge
detector in segmentation process to find the pupil's location. Also, Log-Gabor filter is applied to generate the feature vectors. This method achieved 99% accuracy rate [3]. In 2008, R. Abiyev and K. Altunkaya suggested a fast algorithm for localization of the inner and outer boundaries of iris region using Canny edge detector and circular Hough transform, also, a neural network (NN) was suggested for classification the iris patterns [4]. In 2011, the iris region was encoded using Gabor filters and Hamming distance by S. Nithyanandam [5]. In 2012, Ghodrati et al. proposed a novel approaches for extracting the iris features sing Gabor filters. The Genetic algorithm was proposed to compare two different templates [6]. Gabor approach was more distinctive and compact on feature selection approach. In 2013, G. Kaur [7] suggested two different methods using the Support Vector Machine (SVM). SVM results were FRR=19.8%, FAR = 0%, and overall accuracy rate = 99.9%. Choudhary et al. in 2013 [8], proposed a statistical texture feature depended iris matching method using K-NN classifier. Statistical texture measures include standard deviation, mean, skewness, entropy etc., K-NN classifier matches the current input iris with the trained iris images by computing the Euclidean distance between two irises. The system is tested on 500 iris images, which gives good classification accuracy rate with reduced FRR/FAR. Jayalakshmi and Sundaresan in 2014 [9] proposed K-means algorithm and Fuzzy C-means algorithm for iris image segmentation. The two algorithms were executed separately and the performances of them were 98.20% of accuracy rate with low error rate. In 2015, Homayon [10] suggested a new method based neural network for iris recognition. The proposed method is implemented using LAMSTAR classifier that utilized CASIA-v4.0 database. The accuracy rate was 99.57%. In 2016, A. Kumar and A. Singh suggested a novel method for extracting the feature and the recognition was implemented on 2D discrete cosine transform (DCT). They applied the DCT to extract the most discriminated features in iris [11]. The patterns have been tested on two iris datasets; IIITD and CASIA v.4.0 for matching the iris phase using Hamming distance. The accuracy rate were 98.4% and 99.4% for IITD and CASIA V4 database respectively.
-
III. Iris Recognition System
-
3.1. Image Acquisition
-
3.2. Iris detection, localization, and Segmentation
The proposed system consists of five stages: iris-image acquisition, iris/pupil detection and segmentation, iris normalization, feature generation, and pattern recognition. Figure 2 and 3 shows the flowchart for iris recognition system using two feature extractor methods, the FD and PCA.
The biometric system is constructed using Chinese Academy of Sciences Institute of Automation (CASIA) version 1 database. The image is 320×280 pixels taken from a distance of 4-7 centimeters.
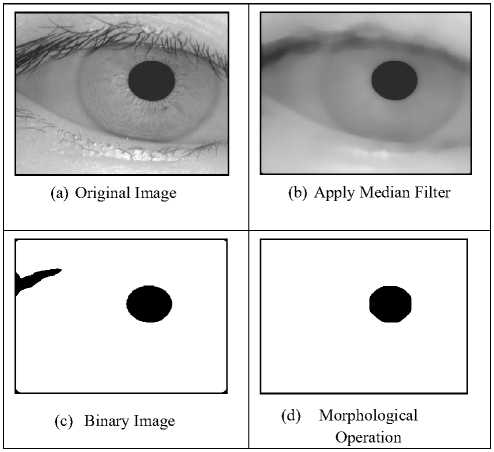
Iris/pupil detection state passes through many operations like smoothing, binarization, and localization. The segmentation state includes two operations: pupil localizing and iris localizing, the two steps are:
-
A. Pupil localization
The pupil region can be detected and localized by the following steps:
Step1: image smoothing using the non-linear median filter
Step2: binarization as in (1).
F(x,y) =
'1
f(x,y) > T
f(x,y) < т
Step3: noise removal using mathematical morphology:
Opening and closing operations
Step4: link the edges by applying the connected component labelling algorithm to
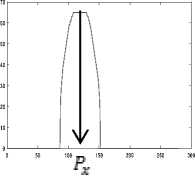
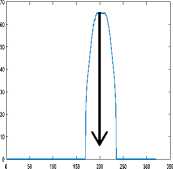
Step5: Find the pupil centers, P x and P y as in (2) and (3), then find the maximum row and column vector as in (4) and (5). See Fig. 2.
x
h(x) = Xall rows(2)
y
v(y) = X all cloumn(3)
Px = max (h)(4)
Py = max (v)(5)
Where:
-
x, y: is the no. of rows and columns respectively
Step6: Find the radius of the pupil (r p ), as in (6)
rp = ( max (h)- min (h))/2(6)
-
B. Iris Localization
-
3.3. Iris Normalization
Canny masks are very useful in locating the iris boundary while the circular Hough transform is applied to complete the circle shape of iris as shown in Fig. 4.
Normalization process minimizes the distortion resultant from pupil motion; it is a vital step for good verification result. First, the iris region is converted from circular shape to a rectangular one, as Fig.5. The rubber sheet model which is founded by Daugman is applied to convert the Cartesian coordinates to polar form model. Polar form provides 20 pixels along r and 240 pixels along θ so an unwrapped strip of 20 × 240 size will stay invariant for image skewing or extension. Equations (7)
and (8) represent a map functions from Cartesian coordinates to polar form (r, θ) are [1]:
X(r,6) = (1 - r)*Xp(6) + r*Xi(6)
Y(r,6) = (1 - r)*Yp(6) + r*Yi(6)
Where,
Xp (6) = Xpo(6) + rp* cos(6)
Yp (6) = Ypo(6) + rp*sin(6)
Xi (6) = Xi0(6) + r* cos(6)(11)
Yi (6) = Yi0(6) + ri*sin(6)(12)
Where:
( X p , Y p ): is the center of the pupil and iris, ( r p , r i ): is the radius of the pupil and iris.
Figure 6 shows the iris normalization and smoothing result.
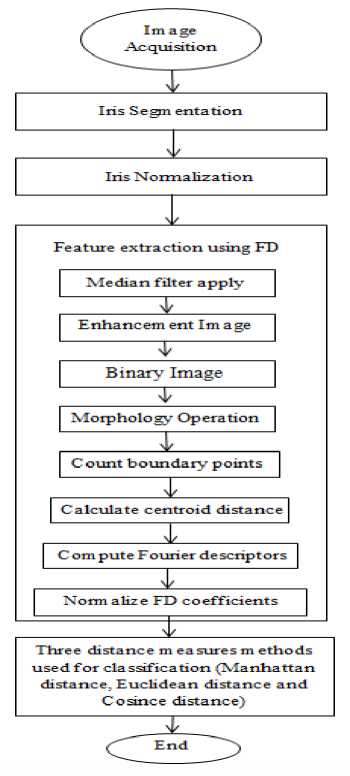
Fig.1. Iris recognition system procedure using FD
Iris Segmentation
T
|
Iris Normalization |
||
|
Feature extraction using PC A |
||
|
Xiedian filter apply |
||
|
Enhancement Image |
||
|
Compute covariance matrix |
||
|
Obtain the eigenvalues |
||
|
Diagonal covariance matrix |
||
|
4' |
||
|
Obtain the eigenvectors |
||
|
Transformation W |
||
|
4- |
||
|
Obtain the transform features |
||
|
Normalize transform features |
||
Three distance measures methods used for classification (Manhattan distance. Euclidean distance and Cosince distance)
Fig.2. Iris recognition system procedure using PCA

(e) Connected Component Labeling
(f) Max Row

(a) Iris normalization

(b) De-noisy image
Fig.6. Iris normalization
P y
(g) Max Column
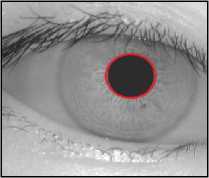
(h) Pupil Localization
Fig.3. Pupil localization steps
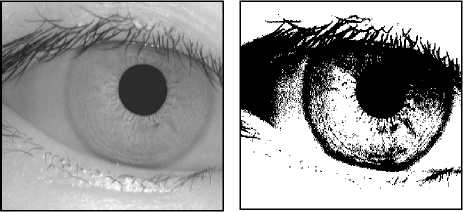
(a) Original Image (b) Binary Image
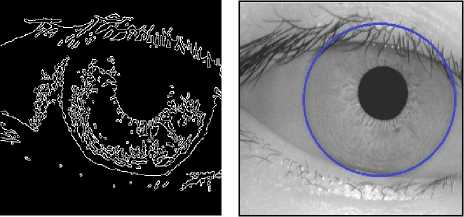
(c) Canny Edge Filter (d) Iris Localization
Fig.4. Iris localization steps
-
3.4. Feature Extraction using Two Techniques
Two different techniques in feature extraction step are applied to create the templates and input vector machine for matching process.
-
A. Fourier Descriptors
There are many techniques for templates creation such: discrete wavelet transform; zero-crossing wavelet; spatial filters; local binary pattern; local variance; 1D local texture pattern and Gabor wavelet. In this work, the FD is used to generate the feature vectors by calculating coefficients of the transformed iris image in frequency domain. The high-frequency coefficients represent the information concerning precise details of the object while the low-frequency coefficients represent the information concerning the general traits of the object. The FD has been successfully used for many applications of the shape representation. The FDs have good characteristics, such as it has robustness to noise, simple derivation and simple normalization. The number of generated coefficients from the shape transformation is commonly large, so sufficient coefficients can be chosen to represent the object features [12, 13]. The FD procedure is: count boundary points, select sampling number (N), calculate centroid distance as in (13),
r(t) = [(t) - - xc] + [y(t) - yc] (13)
Where;
1 N - 1 1 N - 1
xc = — ^ x ( t ) , Ус = _ X У ( t )
c N t = 0 c N t = 0
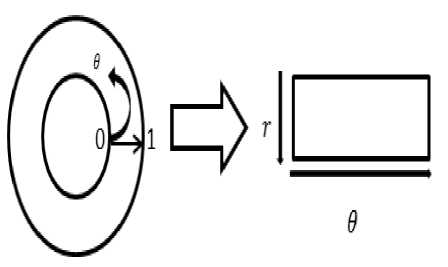
Fig.5. Daugman’s rubber sheet model
The centroid distance indicates to the position of the shape from the boundary coordinates [13]. Calculate Fourier transforms values, as in (14), and then normalize the FD coefficients as in (15).
1 N 1 - 2 jnnn
FD =— X r(t)* exp (------) (14)
n Nt=0 N where n = 0, 1,…N-1.
|
f= |
FD 1 |
FD 2 |
FDN- 1 |
(15) |
|
|
FD 0 |
, |
FD 0 |
FD 0 |
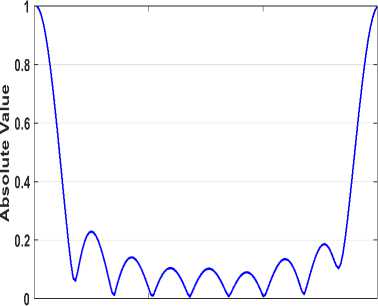
The number of the FD coefficients is large (512 coefficients), thus must be decreased to (150 coefficients) for making the proposed system simple and fast, as in Fig.7.
That represents the diagonal covariance matrix E Y .
Eigenvectors must be linearly independent.
|
\ 1 0 ; |
0 . |
. 0 " |
||
|
E Y = |
λ 2 . |
.. 0 |
(18) |
|
|
_0 |
0 . |
.. λ n J |
0 50 100 150
Number of Coefficients
Fig.7. Iris Signature
-
B. Principle Component Analysis
This approach is known as the Hotelling transform. The major idea of applying PCA is to extract the feature templates. PCA utilizes the factorization to convert data into its statistical properties. This technique is useful for compression, classification and reduction of dimensions. Principal components are a mathematical process, which transforms number of correlated variables into smaller number of uncorrelated variables [14]. PCA procedure is:
Step1: Calculate the covariance matrix ∑X (which X represent feature vectors), as in (16) and (17).
|
° x, 1 , 1 |
σx, 1 , 2 . |
. ° x, 1 ,n |
||
|
E X = |
O x, 2 , 1 |
σx, 2 , 2 . : |
. σx, 2 ,n : |
(16) |
|
_ ° x,n1 |
σ x,n, 2 |
■ ° x,n,n j |
° X« /Е - Г xj*Xj )] (17)
Where,
-
c x,i,j : represent the feature vectors
-
μ x,i,j : represent the mean vector
Step2: compute the eigenvalues and eigenvectors by using characteristic equation:
det( ^.I - X ) = 0.
Step3: compute the transformation matrix T, which represents the eigenvectors as their columns in (19).
|
" T 1 , 1 |
T 1 , 2 . |
. Tin" |
||
|
T = |
T 2 , 1 |
T 2 , 2 . . |
.. T 2 ,n .. |
(19) |
|
. Tn 1 |
Tn, 2 . |
. Tn,n J |
Step4: calculate the transform features,
CY = Cx x W ' or CY=W x Cx ' (20)
The features must be chosen with large values of (λi) [12].
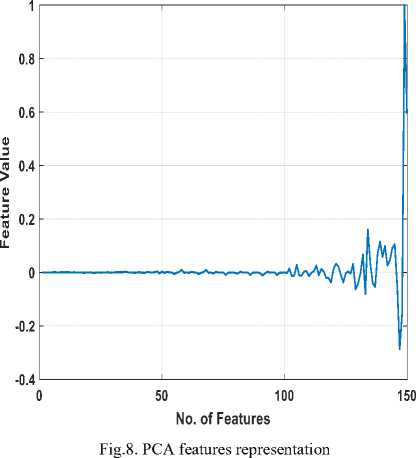
Step5: normalize the features transformation (C Y ), see Fig. 8.
N: represents the number of transform features
-
3.5. Pattern Matching
In matching stage, 300 iris-images were selected for 50 persons; each person has 6 samples in training phase. While in testing phase, 50 iris-images for 50 persons were taken. These images are chosen from CASIA-v1 database. CASIA-v1 close-up iris camera is used for capturing iris images. The resolution of these images is 320*280 with cross-session iris images and extremely clear iris texture details. Manhattan distance, Cosince distance, and Euclidean distance are applied and programmed for executing the classification. The measures distance methods [15] are applied to find the distance between the current template vector and each training templates vectors stored in database. The minimum distance should be checked; if it is less than threshold value that means it is from the same class otherwise it belongs to various classes, the following measures distance ways are:
• Cosince distance
Z (X * Y)
d(X, Y) = 1 - i i = 1 (22)
nn
Z Y 2 * Z X2
N i = 1 i = 1
PCA for three distance approaches (Manhattan, Euclidean and Cosine). This table shows the total running time of iris recognition system for all three distance measurement ways.
No. of accepted imposter
FAR =------------------—----- *100%(25)
Total no. of imposter assessed
No. of rejection genuine
FRR = *100 %(26)
Total no. of genuine assessed
Acc = (-Acj*100%(27)
Where,
NC : represents to the number of correct iris samples.
N : is the total number of iris samples.
• Euclidean distance
d(X,Y) =
n
Z (Xi — Yi) 2
i = 1
• Manhattan distance
n
d(X,Y) = Z X.
i
—
i = 1
Y i
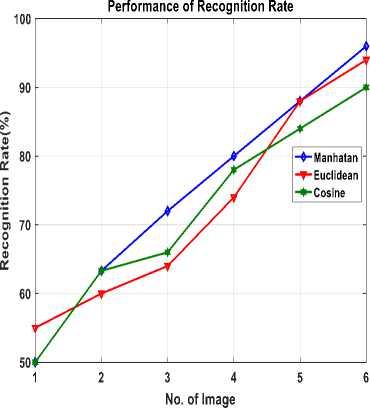
Fig.9. Performance comparison between Manhattan, Euclidean and Cosine distance for FD
IV. Experimental Results
The proposed system is tested for 50 persons; each one has 6 images for training and one image for testing. The iris region is isolated by using some operations such as: morphology operations and connected component labeling algorithm which applied to find the pupil parameters (i.e. radius and center). Canny edge detector and circular Hough transform are applied for finding the iris parameters. Then, iris region is converted from the Cartesian to polar coordinate by Daugman rubber sheet model. Therefore, the rectangular iris image is used for feature extraction as FD and PCA. Three measured distance methods are used for classification. Figure 9 and 10 show the verification performance plots of FD and PCA methods respectively. These figures show that the Manhattan advances Euclidean and Cosine distance for both FD and PCA. Three important standards are utilized for the performance evaluation measurement, they are: False Reject Rate (FRR), False Accept Rate (FAR), and Accuracy rate (Acc) as described in (25, 26, and 27). Table 1 displays the testing performances of FRR, FAR, and Acc rate for iris verification system using FD and
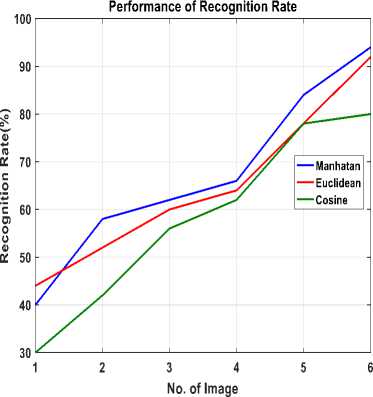
Fig.10. Performance comparison between Manhattan, Euclidean and Cosine distance for PCA
Table 1. Performance comparison between Fourier descriptors and principle component analysis for 50 persons
|
Method |
Distance measures |
FAR% |
FRR% |
Acc% |
Time of training (sec) |
|
FD |
Manhattan |
0.009 |
0.0816 |
96 |
134.203 |
|
Euclidean |
0.012 |
0.1224 |
94 |
138.205 |
|
|
Cosine |
0.041 |
0.2857 |
86 |
138.508 |
|
|
PCA |
Manhattan |
0.008 |
0.1224 |
94 |
191.85 |
|
Euclidean |
0.015 |
0.1632 |
92 |
195.4 |
|
|
Cosine |
0.019 |
0.4081 |
80 |
196.7 |
-
V. Conclusion
A biometric iris recognition system is proposed and implemented using three types of classifiers (Cosine, Euclidian, and Manhattan) and two feature extractor methods to demonstrate the most effective one in recognizing the iris and then defining the human identity. FD was the first feature extraction procedure that chooses the sufficient coefficients from iris signature graph. The second approach is the PCA where a collection of orthogonal basis vectors are created after decreasing the dataset dimensionality to select the most significant feature vectors. The iris localization and segmentation provided 100% accuracy rate. This work has approved that the performance of FD in iris recognition is most effective than PCA. It satisfied 96%, 94% and 86% accuracy rate for Manhattan, Euclidean and Cosine classifiers respectively, while PCA satisfied 94%, 92% and 80% for same classifiers respectively. Manhattan classification results were the best one among Euclidean and Cosine classifiers for both FD and PCA approaches.
Список литературы Biometric system design for iris recognition using intelligent algorithms
- J. Daugman, "How iris recognition works?", IEEE Transactions on Circuits and Systems for Video Technology, Vol. 14, No. 1, pp. 21–30, January 2004.
- B. Son, H. Won, G. Kee, Y. Lee, “Discriminant Iris Feature and Support Vector Machines for Iris Recognition”, in Proceedings of International Conference on Image Processing, vol. 2, pp. 865–868, 2004.
- R.T. Al-Zubi and D.I. Abu-Al-Nadi, "Automated Personal Identification System Based on Human Iris Analysis", Pattern Analysis and Applications, Vol. 10, pp. 147-164, 2007.
- R. Abiyev and K. Altunkaya, "Personal Iris Recognition Using Neural Network", International Journal of Security and its Applications, Vol. 2, No. 2, pp. 41-50, April 2008.
- S. Nithyanandam, K. Gayathri and P. Priyadarshini, "A New IRIS Normalization Process For Recognition System With Cryptographic Techniques", IJCSI International Journal of Computer Science, Vol. 8, Issue 4, No. 1, pp. 342-348, July 2011.
- H. Ghodrati, M. Dehghani, and H. Danyali, "Two Approaches Based on Genetic Algorithm to Generate Short Iris Codes", I.J. Intelligent Systems and Applications (IJISA), pp. 62-79, July 2012.
- G. Kaur, D. Kaur and D. Singh, "Study of Two Different Methods for Iris Recognition Support Vector Machine and Phase Based Method", International Journal of Computational Engineering Research, Vol. 03, Issue 4, pp. 88-94, April 2013.
- D. Choudhary, A. Singh, and S. Tiwari, "A Statistical Approach for Iris Recognition Using K-NN Classifier", I.J. Image, Graphics and Signal Processing (IJIGSP), pp. 46-52, April 2013.
- S. Jayalakshmi and M. Sundaresan, "A Study of Iris Segmentation Methods using Fuzzy C Means and K-Means Clustering Algorithm", International Journal of Computer Applications (0975 – 8887) Vol.85, No 11, January 2014.
- S. Homayon, "Iris Recognition For Personal Identification Using Lamstar Neural Network", International Journal of Computer Science & Information Technology (IJCSIT) Vol. 7, No 1, February 2015.
- A. Kumar, A. Potnis and A. Singh, "Iris recognition and feature extraction in iris recognition system by employing 2D DCT", IRJET International Research in Computer Science and Software Engineering, and Technology, Vol.03, Issue 12, p. 503-510, December 2016.
- M. Nixon and A. Aguado, "Feature Extraction & Image Processing for Computer Vision", third edition, AP Press Elsevier, 2012.
- A. Amanatiadis, V. Kaburlasos, A. Gasteratos and S. Papadakis, "Evaluation of shape descriptors for shape-based image retrieval", The Institution of Engineering and Technology, Vol. 5, Issue 5, pp. 493-499, 2011.
- Saporta G, Niang N. “Principal component analysis: application to statistical process control”. In: Govaert G, ed. Data Analysis. London: John Wiley & Sons; 2009, 1–23.
- R. Porter, "Texture Classification and Segmentation", Ph.D thesis, University of Bristol, November 1997.


