Биполярный закон гравитации

Со времен И. Ньютона и до конца ХХ столетия отличительной чертой гравитации считалось притяжение. И хотя теория относительности допускала, что силы гравитации могут быть отталкивающими, подавляющее большинство физиков и астрофизиков считали, что гравитация лишь замедляет расширение Вселенной. Однако в 1998 году обнаружилось, что Вселенная расширяется с ускорением [1]. Более того, выяснилось, что наблюдаемая Вселенная состоит не менее чем на 95% из небарионной материи, которая не участвует в электромагнитном взаимодействии и потому невидима [2,3]. Исследователи вынуждены были предположить, что либо закон всемирного тяготения не учитывает сил отталкивания, либо в состав небарионной материи наряду с «темным веществом», создающим силы тяготения, входит гипотетическая «темная энергия», ответственная за силы отталкивания, превышающие их именно на такую долю, которая обеспечивает наблюдаемое ускоренное расширение Вселенной. Поскольку же из четырех известных видов взаимодействия для ее масштабов помимо электромагнитного подходит лишь гравитационное взаимодействие, приходится признать, что закон Ньютона нуждается в серьезных дополнениях.

Действительно, для такого вывода имеются веские основания. Если предположить, что этот закон справедлив лишь для барионной (светлой) материи, которая по современным представлениям состоит из протонов, электронов, нейтронов и кварков, то он не может быть отнесен к «всемирным» законам, поскольку неприемлем для 95% вещества Вселенной. Следовательно, необходим закон, удовлетворяющий всем 100% ее вещества.

Известно, далее, что закон Ньютона учитывает только парное взаимодействие тяготеющих тел в отсутствие каких-либо иных тел, участвующих в гравитационном взаимодействии. Это очень далеко от реальности, поскольку материя распределена во Вселенной хоть и неравномерно, но непрерывно.

Немаловажно также, что этот закон признает существование только сил притяжения между ними F g . Согласно этому закону, эта сила для двух тел с массами m и M пропорциональна произведению этих масс и обратно пропорциональна квадрату расстояния между их центрами R 12 :

F g = YmMIR 12 ²

где γ – гравитационная постоянная, равная по современным данным 6,672^10^-11 H^W.

Между тем то, что для одной пары тел выглядит как их притяжение, для другой означает отталкивание, что и породило целый ряд «приталкивательных» теорий гравитации, начиная с Лесажа [4].

Более того, закон тяготения Ньютона (1) не признает существования гравитационного равновесия, характеризующегося обращением в нуль силы тяготения при конечной величине R12 < ^. Между тем в астрономии известно явление либрации — состояния равновесия небесного тела относительно двух других более массивных тел. В существовании такого равновесия легко убедиться на простейшем примере «задачи трех тел», когда пробная массы m, расположенной между массами М1» m и М2 » m на одной линии с ними. В таком случае согласно (1) силы притяжения пробного тела к ним будут равны соответственно Fi = утМ1/R12 и F2 = YmM2/R2, где R1, R - расстояния от пробного тела соответственно до центра 1-го и 2-го тела, а их результирующая Fg обратится в нуль в так называемй «точке либрации», для которой (R1/R2)2 = М1/М2. Это равновесие неустойчиво, поскольку отклонение пробного тела массой m от точки либрации в сторону любого из тел М1 или М2 вызывает дальнейшее их сближение до состояния контакта, а в случае их проницаемости — и слияния. Такого рода неустойчивое равновесие реально наблюдается в тесных системах двойных звезд или галактик, что приводит к перетеканию вещества с одного небесного тела на другое при неизменном положении их центров вплоть до полного исчезновения одного из них.

Известно также, что закон Ньютона (1) справедлив лишь для стационарных условий (случая относительно неподвижных небесных тел), и его применение к удаленным объектам предполагает мгновенное действие гравитационных сил на любом расстоянии. Это также очень далеко от современных представлений.

Дополнительные трудности создает расходимость выражения (1), согласно которому не только сила тяготения F g , но и потенциальная энергия ℰ g гравитационного взаимодействия, а также его потенциал ф д — 8 g / m

8 g = — YmM / R 12 ; ф д — — yM / R 12                      (2)

обращаются в бесконечность по мере сближения тяготеющих тел ( R 12 ^ 0). Между тем математика не способна оперировать бесконечностями.

Вызывает также неудовлетворенность отрицательная величина энергии 8 g и потенциала ф д при ньютоновском определении силы F g , поскольку с позиций термодинамики энергия Вселенной в целом, включающей в себя всю совокупность взаимодействующих материальных объектов («все сущее»), является не внешней, а внутренней, которая не может быть величиной отрицательной. Противоречит отрицательная величина энергии и классическому определению понятия энергии как способности совершать работу. Все это подтверждает вывод о неполноте теории тяготения Ньютона и побуждает к поиску более общего закона взаимодействия масс, из которого закон тяготения Ньютона вытекал бв как частный случай.

Предлагаемое в настоящей обоснование такого закона основано на принципе эквивалентности энергии и массы в его 146

приложении к сплошной среде с неоднородным полем ее плотности. Такой подход является более кратким, нежели предложенный ранее энергодинамический их вывод [5], основанный на междисциплинарной теории переноса и преобразования любых форм энергии [6]. Он не нуждается в привлечении каких-либо гипотез, постулатов и модельных представлений о структуре барионного вещества и микроскопическом «механизме» процессов превращения небарионного вещества в барионное. Такой подход делает его наиболее общим.

2.    Единый закон притяжения и отталкивания масс

Поскольку понятия «гравитационного поля» и «поля тяготения» являются в ряде языков практически синонимами, во избежание недоразумений будем называть единое поле сил притяжения и отталкивания «массодинамическим». Термин «массодинамический» впервые предложен в [7]. В этом термине подчеркивается природу материального носителя этого взаимодействия и его динамический (силовой) характер. Для нахождения напряженности такого поля воспользуемся принципом эквивалентности массы и энергии, который в применении к любой (барионной и небарионной) материи массой М имеет вид ℰ g =Мс ². Отсюда следует, что массодинамический потенциал Ψ g = = d ℰ g /dМ = с ². Поскольку для полевых величин удобнее относить все экстенсивные величины к системе единичного объема, будем оперировать понятием плотности энергии массодинамического поля ℰ v = d ℰ g /dV = ρ с ² (Дж/м³), где ρ – плотность вещества. Тогда по аналогии с электрическим и магнитным полем E и H для характеристики массодинамического поля следует ввести понятие его напряженности Н m = – ∇ℰ v . Эта величина выражается через градиент плотности вещества ∇ ρ простым соотношением:

Н m = – с ² ∇ ρ , (кг/м²∙с²) . (3)

Это выражение будем называть законом массодинамического взаимодействия, поскольку оно связывает между собой все величины, которые его характеризуют. Согласно ему, гравитационное (массодинамическое) поле порождено неоднородным распределением массы, а его напряженность Нm пропорциональна градиенту ее плотности. Поскольку Нm = ρg, то в соответствии с (3) величина ускорения в гравитационном (массодинамическом) поле g пропорциональна относительному градиенту Vp/p плотности вещества:

g = CVq/q , м/с². (4)

. Это положение никоим образом не следовало из закона Ньютона, в котором гравитационная сила F g и ускорение g исчезает только в отсутствие массы M или m. Поэтому закон массодинамического взаимодействия (3) не является обобщением закона Ньютона, а представляет собой нечто новое, имеющее парадигмальное (мировоззренческое) значение.

Выражение (4) подтверждает вывод энергодинамики о том, что ускорение в сплошной среде зависит не только от градиента плотности вещества ∇ ρ, но и от его плотности, так что в межзвездном пространстве с одинаковым ∇ ρ оно будет уменьшаться в более плотных областях Вселенной. Оба этих фактора могут служить объяснением аномальному ускорению космических зондов «Пионер» и «Вояджер-1 и 2» их переходом в область Вселенной с более равномерным его распределением или с несколько большей плотностью межзвездного вещества.

Особенно важно, что согласно (3) и (4), ускоряющая сила Fg всегда направлена против градиента плотности вещества ∇ρ и потому может иметь в различный знак в зависимости от характера распределения вещества в конкретной области пространства Вселенной. Иными словами, гравитационные (массодинамические) силы биполярны, т.е. могут быть как силами притяжения, так и силами отталкивания [4]. Согласно этому положению, характер действующих во Вселенной гравитационных сил может быть определено визуально по характеру распределения в нем барионного (видимого) вещества (галактик, звезд, туманностей и т.п.). Согласно ему, если плотность вещества в центре скопления звезд или галактик спадает к периферии, то действующие на нее массодинамические силы имеют характер сил тяготения. Это объясняет, почему уплотнение вещества в какой-либо области Вселенной, раз возникнув, с течением времени усиливается, возрастая от величины ρ ~10-27 кг/м3до плотности белых карликов (p ~1018 кг/м3). Становится понятным и возникновение «черных дыр» в центрах галактик, которые невидимы не только тогда, когда барионное вещество в них еще не образовалось, но и в конце эволюции галактики, когда тяготение возросло настолько, что препятствует излучению барионного вещества. Становится понятным и причина «взрыва сверхновой», когда плотность возрастает настолько, что относительные градиенты ее плотности уже не выдерживают внутреннего давления, обусловленного протекающими в нем термоядерными реакциями.

Из (3) и (4) следует также, что если при удалении от одного скопления и приближении к другому его плотность возрастает, то со стороны этого второго скопления на первое действуют силы отталкивания. Эти силы и удерживают его на определенном расстоянии от первого. Это положение также не следовало из закона Ньютона, в котором фигурировали только силы тяготения.

Еще одно немаловажное следствие законов гравитации (3) и (4) состоит в том, что в отличие от закона Ньютона они содержат условие гравитационного равновесия ( ∇ ρ = 0). Выполнение этого условия обеспечивает сохранение устойчивой конфигурации любых материальных объектов, начиная от элементарных частиц в атомах и до гигантских скоплений галактик [4], не требуя тонкого баланса центробежных и гравитационных сил. Это равновесие устойчиво, если смещение от положения равновесия вызывает появление «возвращающей» силы, т.е. ускорения, направленного против смещения:

^ Ф g = ^- V g > 0, (5)

и, напротив, неустойчиво, если это смещение вызывает дальнейшее увеличение ускорения тела в том же направлении:

^{V 2}Ф g =^{- V} g < 0, (6)

О наличии зон устойчивого равновесия свидетельствует явление либрации (медленных колебаний положения или траектории движения небесных тел относительно среднего положения). Согласно (5) и (6), «ширина» зоны устойчивого равновесия зависит от величины Vp/p. Там, где относительная неоднородность Vp/p невелика, зоны либрации могут занимать значительную часть пространства Вселенной (подобно равнинным рекам). Однако по мере усиления этой неоднородности эти зоны сужаются и могут исчезнуть вовсе, как это имело место в законе тяготения Ньютона. Подобная же ситуация наблюдается и в так называемых «тесных системах» парных звезд или галактик, где неустойчивость равновесия проявляется в перетекании вещества с одного небесного тела на другое.

Немаловажным в законах (3) и (4) является также зависимость напряженности Н m и ускорения g от скорости распространения возмущений в массодинамическом поле с. В общем случае полная производная по времени от Н m имеет вид:

d H m ( dt = ( e - V ) H m + (д Н m /д t ) г . (7)

Здесь (дН m/д t)г - локальная скорость возмущения массодинамического поля, обусловленная колебаниями плотности вещества ρ в данной точке пространства; (с∙∇)Нm – его конвективная составляющая, обусловленная распространением этого возмущения в пространстве со скоростью с = ǀсǀ. В электродинамике этим составляющим соответствует плотность тока смещения и тока проводимости, а величине ∇Нm – плотность электрического заряда ρе. Выражение (7) можно переписать в виде волны напряженности массодинамического поля Нm дНm /дt + U-дНm/дг = dHmJdt. (8)

Это уравнение относится к классу так называемых кинематических уравнений волны с затуханием d H m / dt , которые отличаются от динамических уравнений 2-го порядка тем, что описывают волну, распространяющуюся в одну сторону (от источника) со скоростью υ [8].

Таким образом, уравнения (3) и (4) учитывают, в отличие от закона Ньютона, конечную скорость распространения гравитационного (массодинамического) взаимодействия, осуществляемого бегущей волной плотности межзведного вещества. Очевидно, что при υ = 0 эти возмущения передаваться не будут. Отсюда следует, что напряженность Н m и ускорение g в массодинамическом поле зависят от скорости распространения в нем возмущений, что соответствует современной концепции близкодействия.

Весьма важным в контексте рассматриваемой задачи является также то обстоятельство, что массодинамические силы различаются по знаку так же, как и электрические и магнитные силы. Тем самым облегчается понимание того, что природа всех сил едина, а все четыре категории сил взаимодействия различаются в конечном счете лишь их дальнодействием, зависящим от свойств «проницаемости»

для них барионной материи. Это открывает прямой путь к «великому объединению» гравитации с электромагнетизмом и построению единой теории массодинамического поля.

3.    Тяготение как частный случай взаимодействия

Как известно, закон тяготения Ньютона позволяет найти гравитационный потенциал ψ g в точке поля вне «полеобразующего» тела массой М ≫ m на расстоянии R от его центра. Этот закон можно распространить на случай однородного полеобразующего тела конечных размеров с эквивалентным радиусом R о и массой М = ρ V. Такой подход более соответствует реалиям и условиям опыта Кавендиша, проводившегося со свинцовыми шарами конечных размеров. Поскольку работа, совершаемая гравитационным полем при сближении точечного пробного тела с таким полеобразующим телом возможна только до расстояния R = R о , эту конфигурацию тел и следует принять за начало отсчета потенциала ψ g . При такой «калибровке» их гравитационная энергия рассматриваемой пары тел определится выражением:

ℰ g = γmМ (1/ R o – 1/ R ). (8)

В этом выражении началом отсчета служит состояние с минимальной гравитационной энергией ( R = R o ), так что гравитационная энергия становится величиной сугубо положительной, а расходимости сил F g , энергии ℰ g , потенциала ψ g и ускорения g = – ∇ ψ g в законах Ньютона не возникает, поскольку R o > 0. С позиций термодинамики такая калибровка является единственно допустимой, поскольку Вселенная в целом, включающая всю совокупность взаимодействуюших материальных объектов (все «сущее») является изолированной системой, а ее полная энергия, включая гравитационную ℰ g , становится не внешней, а внутренней, которая не может быть величиной отрицательной.

Однако и при такой калибровке энергии гравитационный потенциал ψg = ψg(М, R), т.е. остается функцией массы полеобразующего тела и положения пробного тела, как и в законе Ньютона. Поставим теперь задачу найти потенциал ψg на одном и том же удалении от центра массы небесного тела, (например, на поверхности сферы единичного объема V с радиусом R =const) в функции плотности этого тела ρ, т.е. ψg = ψg(ρ), как и в выражении (3). Тогда в соответствии с законом Ньютона g = – ∇ψg = – (γV/R)∇ρ/ρ = ψg∇ρ/ρ. (9)

Таким образом, ив этом случае ускорение g оказывается связанным с градиентом плотности сходным с (4) выражением с тем лишь отличием, что коэффициент пропорциональности с ² в нем заменен на ψ g . Следовательно, закон Ньютона следует рассматривать как частный случай более общего закона массодинамического взаимодействия, Возникает, однако, закономерный вопрос, почему в таком случае закон Ньютона не отражает наличия биполярности сил тяготения? Ответ на этот кроется в существующем произволе в выборе начала отсчета энергии в механике, при котором вполне допустимо принять за него положение центра массы М = ρ V «полеобразующего» тела, а общую для взаимодействующих тел потенциальную энергию целиком приписать другому телу, находящемуся в его «поле». Тогда градиент (перепад) плотности в направлении любого из взаимодействующих с ним тел будет величиной положительной, а гравитационная сила – только силой тяготения.

Другое отличие ньютоновского закона гравитации состоит в том что величина гравитационного потенциала в нем ψ g на много порядков меньше, чем массодинамический потенциал Ψ m , найденный из принципа эквивалентности массы и энергии. Чтобы убедиться в относительной малости ньютоновского потенциала ψ g , воспользуемся предложенной выше «перенормировкой» закона Ньютона (8), которая позволяет найти максимальную величину гравитационного потенциала ψ g , создаваемого тем или иным небесным телом.

Действительно, согласно закону Ньютона (2) гравитационный потенциал ψg тела конечных размеров максимален по абсолютной величине при R = Rо, где он равен ǀψgоǀ = =(γV/Rо)ρ. Это максимальное значение уже можно сопоставить с Ψgg = с2~ 9∙1016 Дж/кг. В частности, для Солнца с массой М = 1,989 ∙1030 кг и радиусом Ro = 6,9599∙108 м имеем ψg = 1,906∙1011 Дж/кг. Подобным образом для Земли с массой М = 5,976 ∙1024 кг и радиусом Ro = 6,36∙106 м находим ψg = 6,27∙107 Дж/кг. Это свидетельствует о чрезвычайной малости ньютоновского гравитационного потенциавла и о существовании в природе так называемой «сильной гравитации» [9] (точнее, о значительном превышении массодинамического потенциала Ψg над ньютоновским ψg).

Одной из причин такой их несопоставимости является тот факт, что массодинамический потенциал (6) учитывает взаимодействие всех элементов материи со всеми, а не только парные взаимодействия, как закон Ньютона. Кроме того, ньютоновский потенциал ψ g де-факто является величиной относительной, в то время как Ψ g = с ² – величина абсолютная. Это непосредственно следует из самого принципа эквивалентности массы и энергии ℰ g =М g с ², согласно которому потенциал Ψ g отсчитывается от абсолютного нуля, соответствующего полному отсутствию каких-либо масс вне взаимодействующей пары. В таком случае соотношение между Ψ g и ψ g целиком зависит от состояния начала отсчета, что в принципе противоречит термодинамике с ее понятием абсолютной температуры, абсолютного давления и т.п. Ведь совершенно очевидно, что работа перемещения W единицы массы пробного тела из одной точки гравитационного поля в любую другую будет равна нулю, если это поле однородно.

Вполне объяснимо и отсутствие в законе Ньютона сил отталкивания. Это связано опять-таки с произволом в выборе начала отсчета потенциальной энергии в механике. В самом деле, когда рассматривается пара тел, вполне естественно выбрать за начало отсчета расстояния R 12 центр массы полеобразующего тела, а потенциальную энергию рассматриваемой пары взаимодействующих тел приписать пробному телу, находящемуся «в поле» другого тела. В таком случае как градиент, так и перепад плотности вещества в таком поле согласно выражениям (3) и (4) будет величиной положительной, а сила F g – отрицательной, т.е. силой тяготения. Таким образом, мы приходим к выводу, что закон Ньютона является частным случаем более общего и биполярного закона массодинамического взаимодействия.

4.    Экспериментальное подтверждениетеории

Убедительное подтверждение большинства следствий из законов (3) и (4) можно найти из полученных недавно в лаборатории имени Лоуренса в Беркли (США) данных о распределении галактик в видимой части Вселенной [10]. Основной целью исследований этой лаборатории в рамках грандиозного проекта цифрового обзора неба (SDSS) было максимально точное (достигшее на сегодняшний день 1%) вычисление координат полутора миллионов звездных скоплений и составление трехмерной карты звездного неба. Анализируя картину распределения 1,2 миллионов таких скоплений, ученые обнаружили повторяющиеся сферические волновые структуры, которые в разрезе (на фиксированном расстоянии от наблюдателя) выглядели как кольцевые структуры (рис.1). Как следует из рисунка, галактики в таких структурах сосредоточены в основном либо в их центре, либо на периферии, что было интерпретировано ими как барионные акустические осцилляции межзвездного вещества Вселенной [11]. Такой характер распределения видимого вещества во Вселенной хорошо согласуется с законом массодинамического взаимодействия (3). Согласно ему, силы тяготения Fg = mg всегда направлены в сторону, противоположную градиенту плотности ∇ρ. Это мы и наблюдаем в центральных скоплениях (ядрах) галактик, в которых плотность звездных скоплений убывает по мере удаления от их центра (что соответствует силам тяготения, ускоряющим его сжатие). То же самое наблюдается и в периферийны кольцевых структурах, где плотность звездных скоплений убывает в обе стороны от центральной (осевой) линии кольца. В то же время между центральными и периферийными скоплениями звезды практически отсутствуют, что свидетельствует об отсутствии в этих областях условий для уплотнения небарионной материи и превращения ее в барионное вещество. Поскольку таким условием является наличие градиентов плотности, приводящих к уплотнению небарионного вещества и его последующей «конденсации», можно заключить о наличии во Вселенной обширнейших «зон либрации», где соблюдается равенство сил притяжения и отталкивания, т.е. поддерживается состояние равновесия (∇ρ = 0).

То обстоятельство, что периферийные скопления галактик удерживаются на значительном расстоянии от центрального скопления (равном приблизительно 500 миллионам парсек) [11], свидетельствует о наличии между центральными и периферийными скоплениями галактик сил отталкивания. Наличие этих сил, предсказанное уравнением (3), делает излишним введение «темной энергии» как гипотетической среды с отрицательным давлением, призванной уравновешивать (с некоторым избытком) силы тяготения и тем самым обеспечивать ускоренное расширение Вселенной [12]. Таким образом, точная карта Вселенной, явившаяся триумфом наблюдательной астрономии, подтверждает основные выводы, вытекающие из закона массодинамического взаимодействия. Поскольку же этот закон затрагивает самые общие проблемы мироздания, он открывает перспективы серьезного прорыва и в других областях знания [13].

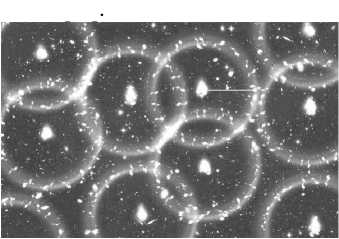
Рис. 1. Карта Вселенной с изображением кольцевых структур (Source: Berkeley National Laboratory)